【因果推断python】8_线性回归模型2
目录
回归理论
非随机数据的回归
回归理论
我不打算深入研究线性回归是如何构建和估计的。然而,一点点理论将有助于解释它在因果推断中的力量。首先,回归解决了理论上的最佳线性预测问题。令 是一个参数向量:
线性回归找到最小化均方误差 (MSE) 的参数。
如果你对上述等式进行微分并将其置零,你会发现这个问题的线性解由下式给出
面对样本估计的时候,我们可以使用等价如下公式估计这个 beta:
但不要只看上面的论述。如果相对钻研公式,您更喜欢直接写代码,那么不妨自己尝试一下:
X = data[["format_ol"]].assign(intercep=1)
y = data["falsexam"]def regress(y, X): return np.linalg.inv(X.T.dot(X)).dot(X.T.dot(y))beta = regress(y, X)
betaarray([-4.9122215 , 78.54748458])上面的公式很笼统。 然而,我们研究只有一个回归变量的情况是值得的。 在因果推断中,我们经常想估计变量 T 对结果 y 的因果影响。 因此,我们使用带有这个单一变量的回归来估计这种影响。 即使我们在模型中包含其他变量,它们通常也只是辅助变量。 添加其他变量可以帮助我们估计干预的因果效应,但我们对估计它们的参数不是很感兴趣。
对于单个回归变量 T,与其关联的参数将由下式给出
如果 T 是随机分配的,则 是 ATE。
kapa = data["falsexam"].cov(data["format_ol"]) / data["format_ol"].var()
kapa-4.912221498226952如果我们有多个回归量,我们可以扩展以下公式来适应这一点。假设那些其他变量只是辅助变量,我们真正感兴趣的只是估计与T 关联的参数 。
可以通过以下公式获得
其中 是所有其他协变量
在
上回归的残差。现在,让我们欣赏一下这有多酷。这意味着多元回归的系数是在考虑模型中其他变量的影响后相同回归量的双变量系数。在因果推断方面,
是 T 在使用所有其他变量进行预测后的双变量系数。
这背后有一个很好的直觉解释。如果我们可以使用其他变量来预测 T,那就意味着它不是随机的。但是,一旦我们控制了其他可用变量,我们就可以使 T 与随机一样好。为此,我们使用线性回归从其他变量预测它,然后我们取该回归的残差 。根据定义,
不能被我们已经用来预测 T的其他变量 X 预测。非常优雅地,
是一种与X 中的任何其他变量无关的处理版本。
顺便说一下,这也是线性回归的一个特性。残差始终与创建它的模型中的任何变量正交或不相关:
e = y - X.dot(beta)
print("正交意味着矩阵相乘结果为0", np.dot(e, X))
X[["format_ol"]].assign(e=e).corr()更酷的是,这些属性不依赖于任何东西!无论您的数据是什么样子,它们都是数学真理。
非随机数据的回归
到目前为止,我们使用的是随机实验数据,但正如我们所知,这些数据很难获得。进行实验的成本非常高,或者根本不可行。很难说服麦肯锡公司随机免费提供他们的服务,以便我们能够一劳永逸地将他们的咨询服务带来的价值与那些有能力支付他们的公司已经很好的事实区分开来离开。
出于这个原因,我们现在将深入研究非随机或观察数据。在以下示例中,我们将尝试估计多受教育一年对小时工资的影响。正如您可能已经猜到的那样,进行教育实验是极其困难的。你不能简单地将人们随机分配到 4、8 或 12 年的教育中。在这种情况下,我们只有观察数据。
首先,让我们估计一个非常简单的模型。我们将对受教育年限的小时工资进行回归。我们在这里使用对数,以便我们的参数估计有一个百分比解释。有了它,我们就可以说多接受 1 年的教育会使工资增加 x%。
wage = pd.read_csv("./data/wage.csv").dropna()
model_1 = smf.ols('np.log(hwage) ~ educ', data=wage.assign(hwage=wage["wage"]/wage["hours"])).fit()
model_1.summary().tables[1]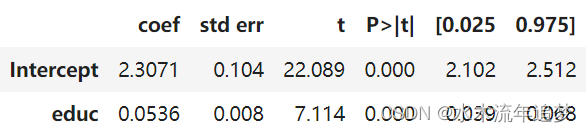
的估计值为 0.0536,95% 的置信区间为 (0.039, 0.068)。 这意味着该模型预测,每增加一年的教育,工资将增加约 5.3%。 这一百分比增长符合教育以指数方式影响工资的信念:我们预计从 11 年到 12 年的教育(平均到高中毕业)比从 14 到 16 年(平均到毕业 大学)。
from matplotlib import pyplot as plt
from matplotlib import style
style.use("fivethirtyeight")x = np.array(range(5, 20))
plt.plot(x, np.exp(model_1.params["Intercept"] + model_1.params["educ"] * x))
plt.xlabel("Years of Education")
plt.ylabel("Hourly Wage")
plt.title("Impact of Education on Hourly Wage")
plt.show()
当然,并不是因为我们可以估计这个简单的模型是正确的。请注意我是如何小心地用我的话来预测来自教育的工资。我从来没有说过这个预测是因果关系。事实上,到现在为止,您可能有非常严重的理由相信这个模型是有偏见的。由于我们的数据并非来自随机实验,因此我们不知道受教育程度高的人和受教育程度低的人是否具有可比性。更进一步,根据我们对世界运作方式的理解,我们非常确定它们没有可比性。也就是说,我们可以争辩说,那些受教育年限更长的人可能拥有更富裕的父母,而且随着教育程度的提高,我们看到的工资增长只是家庭财富与受教育年限的关系的反映。用数学来说,我们认为,也就是说,那些受教育程度高的人无论如何都会有更高的收入,即使没有这么多年的教育。如果你对教育真的很冷淡,你可以争辩说它甚至可以通过让人们远离劳动力和降低他们的经验来减少工资。
幸运的是,在我们的数据中,我们可以访问许多其他变量。我们可以看到父母的教育‘meduc’、‘feduc’、那个人的‘IQ’分数、经验年数‘exper’以及他或她在当前公司的任期‘tenure’。我们甚至有一些关于婚姻和黑人种族的虚拟变量。
wage.head()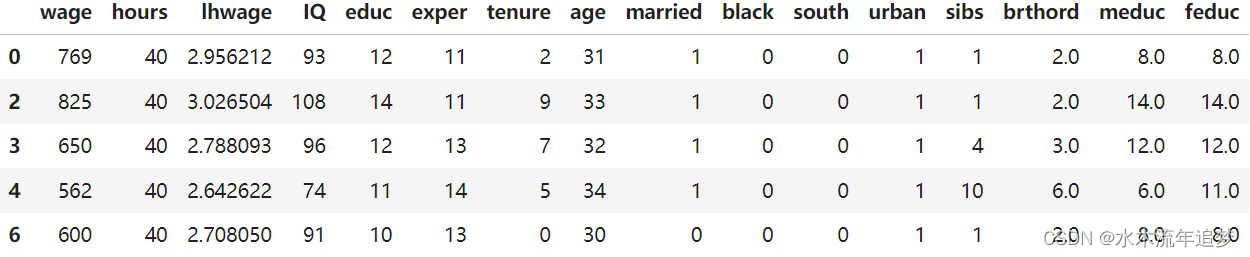 我们可以在模型中包含所有这些额外变量并对其进行估计:
我们可以在模型中包含所有这些额外变量并对其进行估计:
要了解这如何帮助解决偏差问题,让我们回顾一下多元线性回归的二元细分。
这个公式说我们可以根据父母的教育、智商、经验等来预测“edu”。在我们这样做之后,我们将得到一个版本的 edu,,它与之前包含的所有变量都不相关。这将打破诸如“受过更多教育年限的人因为他们的智商更高而拥有它。教育不会导致更高的工资的情况。只是与智商相关的情况,这就是推动工资”。好吧,如果我们在我们的模型中包含 IQ,那么
将成为额外一年教育的回报,同时保持 IQ 不变。暂停一下以了解这意味着什么。即使我们不能使用随机对照试验来保持治疗和未治疗之间的其他因素相等,回归可以通过在模型中包含这些相同的因素来做到这一点,即使数据不是随机的!
controls = ['IQ', 'exper', 'tenure', 'age', 'married', 'black','south', 'urban', 'sibs', 'brthord', 'meduc', 'feduc']X = wage[controls].assign(intercep=1)
t = wage["educ"]
y = wage["lhwage"]beta_aux = regress(t, X)
t_tilde = t - X.dot(beta_aux)kappa = t_tilde.cov(y) / t_tilde.var()
kappa0.04114719101005263我们刚刚估计的这个系数告诉我们,对于具有相同智商、经验、任期、年龄等的人,我们应该预期多受教育一年与每小时工资增长 4.11% 相关。 这证实了我们的怀疑,即第一个只有 edu 的简单模型是有偏见的。 它还证实,这种偏见高估了教育的影响。 一旦我们控制了其他因素,教育的估计影响就会下降。
如果我们更聪明并使用其他人编写的软件而不是自己编写所有代码,我们甚至可以在这个估计值周围放置一个置信区间。
model_2 = smf.ols('lhwage ~ educ +' + '+'.join(controls), data=wage).fit()
model_2.summary().tables[1]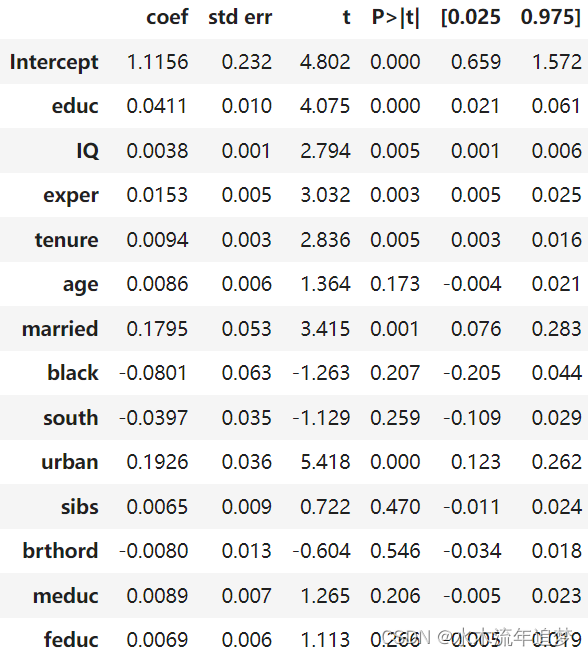
相关文章:

【因果推断python】8_线性回归模型2
目录 回归理论 非随机数据的回归 回归理论 我不打算深入研究线性回归是如何构建和估计的。然而,一点点理论将有助于解释它在因果推断中的力量。首先,回归解决了理论上的最佳线性预测问题。令 是一个参数向量: 线性回归找到最小化均方误差 (…...

MySQL目录和文件
MySQL目录和文件 bin目录 存储一些mysql脚本比如mysqld、mysqld-self等等,用于执行mysql一些操作 数据目录 show variables like datadir;--查看数据目录位置每一个数据库都有一个和数据库名相同的文件夹;MySQL5.7开始每创建一个表,在Innod…...

0基础学习Elasticsearch-Quick start
文章目录 1 背景2 前言3 快速部署ES4 快速部署Kibana5 发送请求给ES5.1 打开Kibana控制台5.2 通过REST API发送请求5.3 通过curl发送请求5.4 添加数据5.4.1 添加单个document5.4.2 添加多个document 5.5 搜索数据5.5.1 搜索所有documents5.5.2 match查询 6 总结 1 背景 因电商项…...
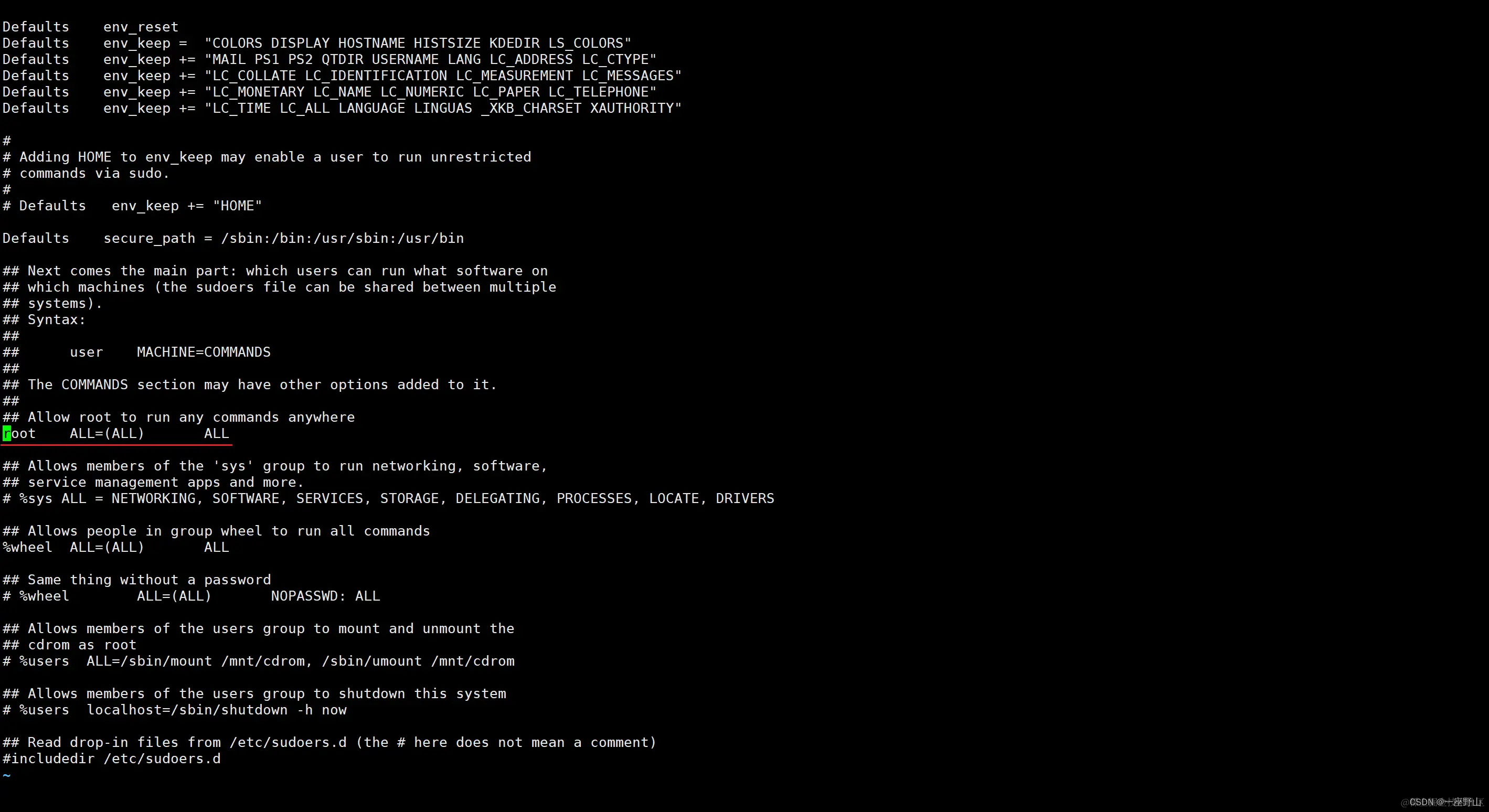
Centos给普通用户添加sudo命令权限
打开sudoers文件 sudo visudo 修改sudoers文件 找到root ALL(ALL) ALL这一行,即如下图标出红线的一行 在此行下新增如下内容: lbs为用给予sudo执行权限的用户名 # 执行sudo命令,需要输入命令 lbs ALL(ALL) ALL 或 # 执行sudo命令,…...

编写备份MySQL 脚本
目录 环境准备 增量备份 增量备份和差异备份 完整代码如下 测试脚本是否正常 星期天运行脚本(完全备份) 星期一运备份脚本(增量备份) 星期二备份数据(其他天--增量备份) 星期三备份数据(差异备…...

C语言中的数据类型转换:隐式类型转换与显示类型转换
一. 简介 本文简单学习一下,C语言中的数据类型转换。重点学习一下隐式类型转换。 二. C语言中的数据类型转换:隐式类型转换与显示类型转换 类型转换(TypeCasting):在C语言中是将一种数据类型值转换为另一种数据类型…...

Android 安卓通过bindService ServiceConnection 没有响应的问题
bindService 失败且 ServiceConnection 没有响应可能由多种原因造成。以下是一些可能的原因和相应的解决方法: Service未正确声明或注册: 如果Service没有在AndroidManifest.xml文件中正确声明或注册,bindService将会失败。解决方法…...
)
python切片(彻底解除对切片的曲解)
sequence[start:stop:step] **start: **step为正时默认为0,step为负时默认为-1 stop:_ step为正时默认为结尾结束,step为负时默认为开始位置_ ss=“abcdefg” 以该字符串举例,ss[start:stop:step]的意思是将字符串ss从start开始截取(包括start),截取到stop(不包括sto…...

Java—— StringBuilder 和 StringBuffer
1.介绍 由于String的不可更改特性,为了方便字符串的修改,Java中又提供了StringBuilder和Stringbuffer类,这两个类大部分功能是相同的,以下为常用方法: public static void main(String[] args) {StringBuilder sb1 n…...

vs2019 c++20 规范 STL库中关于时间的模板
在学习线程的时候,一些函数会让线程等待或睡眠一段时间。函数形参是时间单位,那么在 c 中是如何记录和表示时间的呢?以下给出模板简图: 谢谢...

激光焊接机作为一种高效、精密的焊接设备
激光焊接机是一种用于材料加工时激光焊接的机器,以下是对其的详细介绍: 1. 定义与别称: 激光焊接机,又常称为激光焊机、镭射焊机,是材料加工激光焊接时用的机器。 2. 工作原理: 激光焊接是利用高能量…...

vite为什么速度快
原因 vite快的原因是因为 vite在开发环境中是使用的 esbuild,esbuild 是 go 写的,go 编译型语言、多线程,nodejs 解释型语言、单线程,并且 vite 使用了原生 esm 导入的,所以快一点,当然,这也…...

Java网络编程(下)
White graces:个人主页 🙉专栏推荐:Java入门知识🙉 🙉 内容推荐:Java网络编程🙉 🐹今日诗词:姑苏城外寒山寺,夜半钟声到客船🐹 ⛳️点赞 ☀️收藏⭐️关注💬卑微小博主…...
APISIX的安装与测试(springboot服务测试)
安装: 1.1安装依赖: curl https://raw.githubusercontent.com/apache/apisix/master/utils/install-dependencies.sh -sL | bash -1.2 安装 OpenResty yum-config-manager --add-repo https://openresty.org/package/centos/openresty.reposudo yum i…...

AI技术:探索未来智能的无限可能
随着科技的飞速发展,人工智能(AI)技术已经成为我们这个时代最引人瞩目的科技力量。从简单的自动化任务到复杂的决策支持系统,AI技术正在以前所未有的速度改变着我们的世界。本文将深入探讨AI技术的定义、发展历程、当前应用、面临…...

npm install 出错,按照版本不匹配解决
一、现象 npm install npm WARN config global --global, --local are deprecated. Use --locationglobal instead. npm ERR! code ERESOLVE npm ERR! ERESOLVE unable to resolve dependency tree npm ERR! npm ERR! While resolving: panshi-main-web0.1.0 npm ERR! Found…...
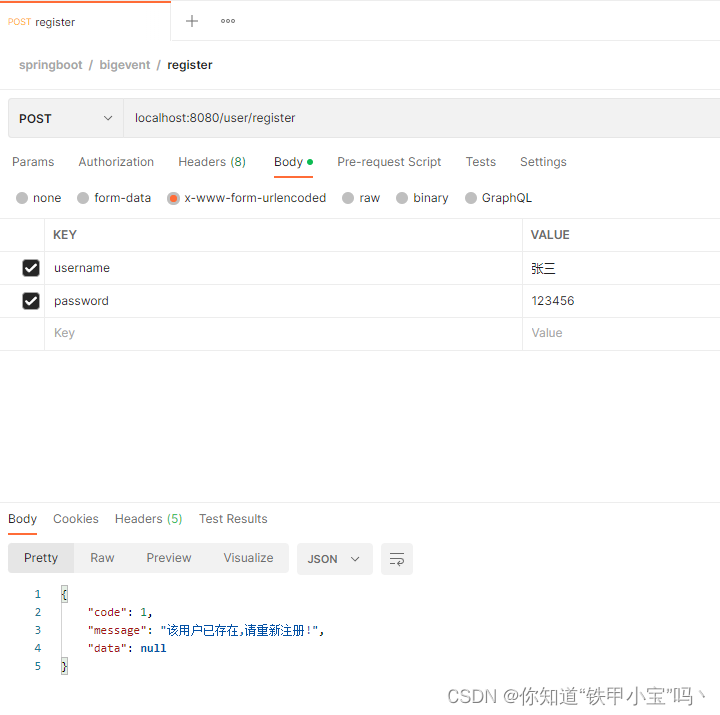
【第1章】SpringBoot实战篇之注册接口
文章目录 前言一、代码部分1. User2.UserMapper13. UserSerivce4. UserController15. Result 二、测试1.注册2.再次注册 总结 前言 下面介绍用户注册接口。 一、代码部分 1. User package org.example.springboot3.bigevent.entity;import com.baomidou.mybatisplus.annotat…...

代码随想录-Day25
216.组合总和III 找出所有相加之和为 n 的 k 个数的组合,且满足下列条件: 只使用数字1到9 每个数字 最多使用一次 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。 示例 1: 输入: k 3, n 7 输…...
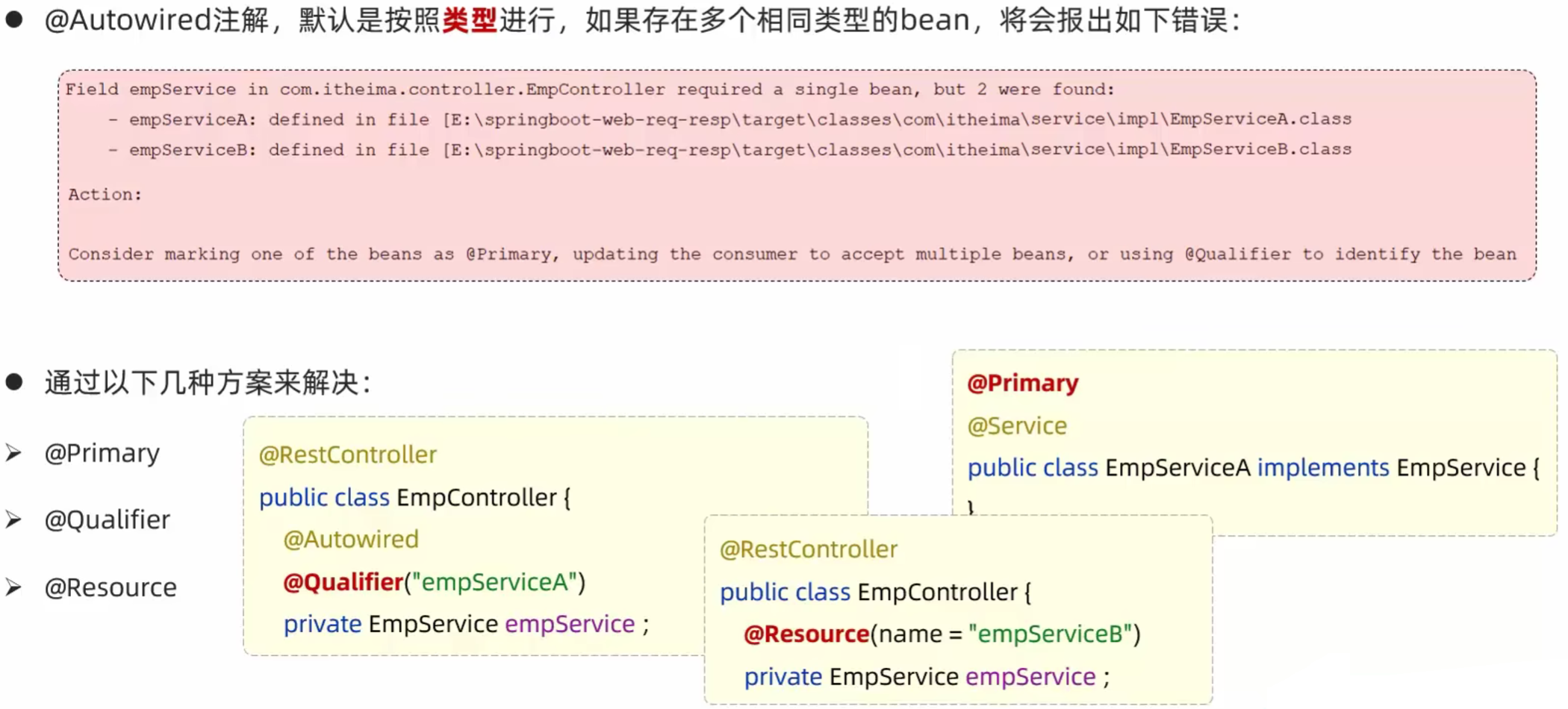
JavaWeb_SpringBootWeb基础
先通过一个小练习简单了解以下SpringBootWeb。 小练习: 需求:使用SpringBoot开发一个Web应用,浏览器发起请求/hello后,给浏览器返回字符串"Hello World~"。 步骤: 1.创建SpringBoot项目,勾选We…...

Stable Diffusion生成图片的参数查看与抹除方法
前几天分享了几张Stable Diffusion生成的艺术二维码,有同学反映不知道怎么查看图片的参数信息,还有的同学问怎么保护自己的图片生成参数不会泄露,这篇文章就来专门分享如何查看和抹除图片的参数。 查看图片的生成参数 1、打开Stable Diffus…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...
:处理原始数据命令)
ffmpeg(三):处理原始数据命令
FFmpeg 可以直接处理原始音频和视频数据(Raw PCM、YUV 等),常见场景包括: 将原始 YUV 图像编码为 H.264 视频将 PCM 音频编码为 AAC 或 MP3对原始音视频数据进行封装(如封装为 MP4、TS) 处理原始 YUV 视频…...

ubuntu清理垃圾
windows和ubuntu 双系统,ubuntu 150GB,开发用,基本不装太多软件。但是磁盘基本用完。 1、查看home目录 sudo du -h -d 1 $HOME | grep -v K 上面的命令查看$HOME一级目录大小,发现 .cache 有26GB,.local 有几个GB&am…...

React与原生事件:核心差异与性能对比解析
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
