【图像处理与机器视觉】频率域滤波
知识铺垫
复数
C=R+jI 可以看作复平面上的点,则该复数的坐标为(R,I)
欧拉公式
e j θ = c o s θ + j s i n θ e^{j\theta} = cos \theta + j sin \theta ejθ=cosθ+jsinθ
极坐标系中复数可以表示为: C = ∣ C ∣ ( c o s θ + j s i n θ ) C = |C|(cos\theta + j sin \theta) C=∣C∣(cosθ+jsinθ)
所以,由于欧拉公式可以将复数表示为: C = ∣ C ∣ e j θ C=|C|e^{j\theta} C=∣C∣ejθ
傅立叶级数
傅立叶指出,任何周期函数都可以表示为不同频率的正弦和余弦函数之和,每个正弦项和余弦项均乘以不同的系数
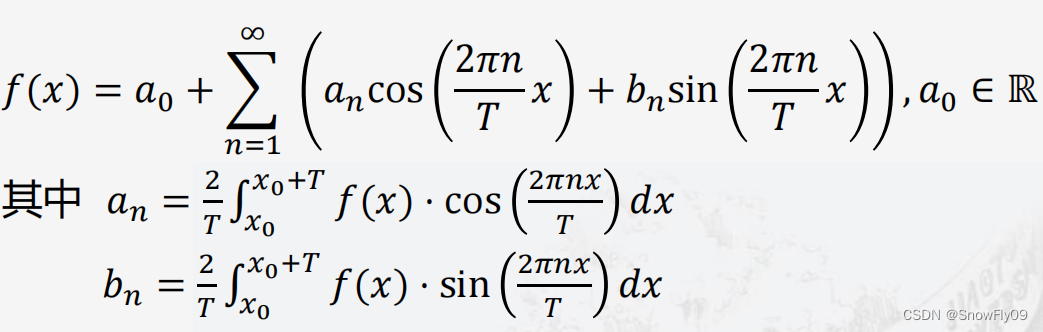
同时,根据我们前面掌握的欧拉公式,可以对傅里叶级数的公式进行转换得到:
f ( t ) = ∑ n = − ∞ ∞ c n ⋅ e j 2 π n T t f(t)=\sum\limits_{n=-\infty}^{\infty}c_n\cdot e^{j\frac{2\pi n}{T}t} f(t)=n=−∞∑∞cn⋅ejT2πnt
傅立叶变换
这里我们不对傅立叶变换的一系列公式推导进行阐述,只对最后我们所使用的离散傅立叶变换进行研究:
对于一个离散序列,我们可以进行傅立叶变换,被称为离散傅立叶变换(DFT):
F ( u ) = ∑ x = 0 M − 1 f ( x ) e − j 2 π u x / M F(u)=\sum\limits_{x=0}^{M-1}f(x)e^{-j2\pi ux/M} F(u)=x=0∑M−1f(x)e−j2πux/M
则其对应的离散傅立叶反变换为:
F ( u ) = 1 M ∑ x = 0 M − 1 f ( x ) e j 2 π u x / M F(u)=\frac{1}{M}\sum\limits_{x=0}^{M-1}f(x)e^{j2\pi ux/M} F(u)=M1x=0∑M−1f(x)ej2πux/M
同理,可以有二维的傅立叶变换 和傅立叶反变换:
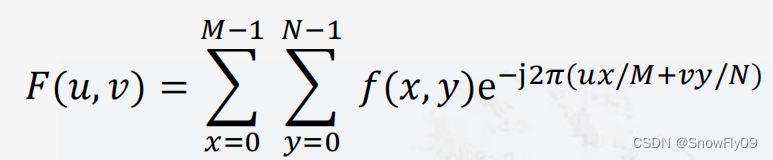
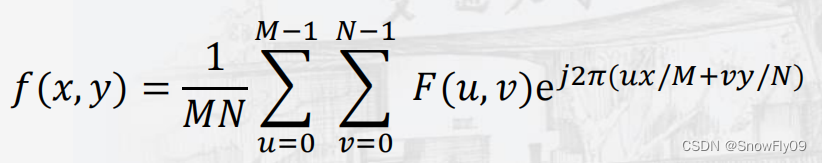
(1)傅立叶变换满足平移性质
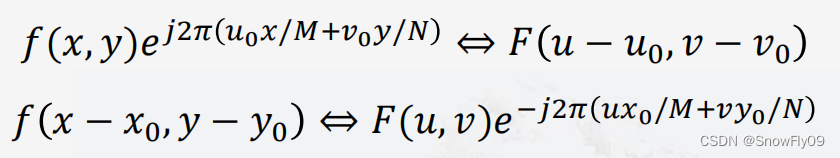
(2)尺度变换
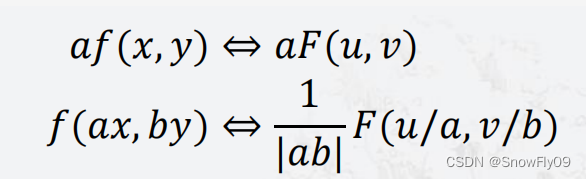
(3)旋转性
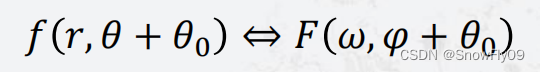
(4)周期性:傅立叶变换具有周期性
(5)平均值:
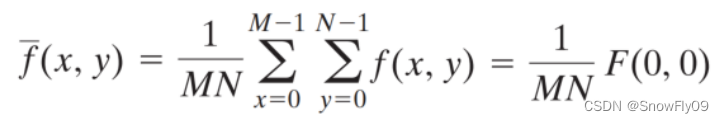
(5)卷积:一个域的卷积是另一个域的乘积
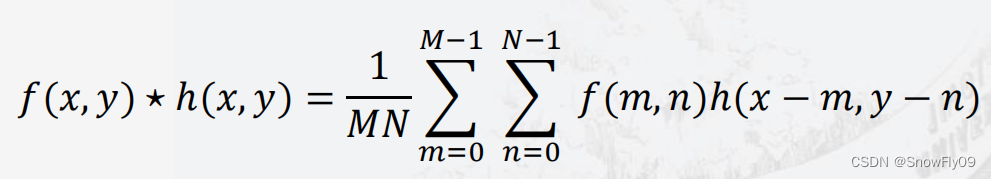

傅立叶变换在图像处理中的实操
请见我另外一篇博客:待补充
频率域滤波
频率域与空间域的对应关系
由我们刚刚知道的平均值,可以知道在空间域中灰度变化缓慢(二阶导小)的频率分量在频率域接近中心的位置;离原点越远,越来越高的频率对应的就是图像中变化较快的灰度(二阶导大),通常对应了图像中的边和细节

因此只允许中间变量通过的滤波器叫做低通滤波器,而允许四周频率通过的滤波器叫做高通滤波器,频率与滤波就是变换一张图的傅立叶变换(通常方式为频率域内乘上不同的滤波器,也即在空间域中进行卷积),再计算其反傅立叶变换得到修改后的空间域的照片
低通滤波器
理想低通滤波器
只通过固定范围内的低频,其他全部不通过
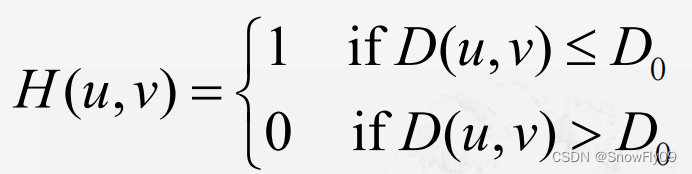
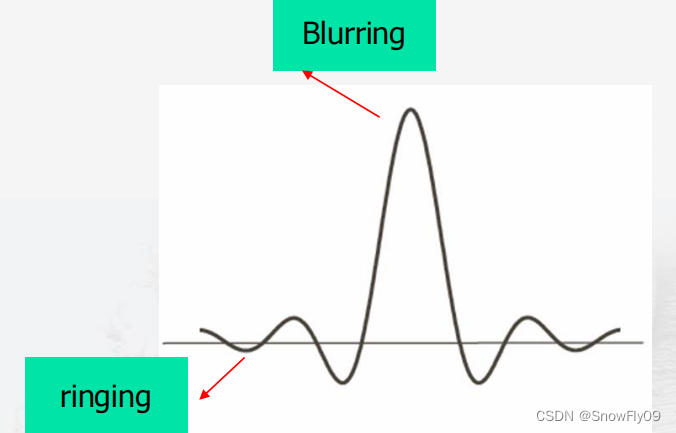
可以对图像进行平滑,但是会存在振铃的现象,原本图像中的边缘出现一圈一圈的虚影,就像水纹一样,主要原因是高频与低频被生硬的切割开了,就如同灰度级较少时生硬的切割会形成伪轮廓一样
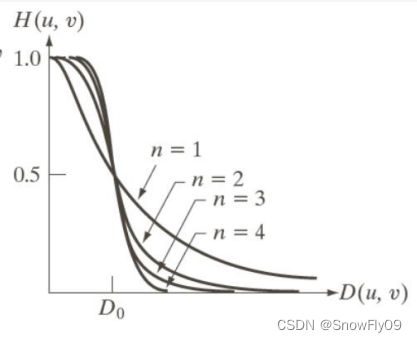
布特沃斯低通滤波器
通过缓和的高频和低频的过渡有效去除了振铃现象
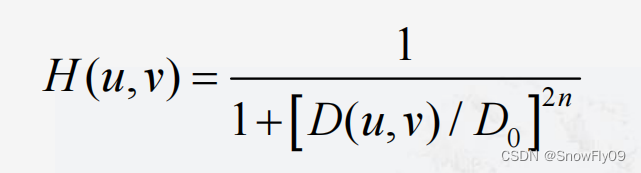
高斯低通滤波器
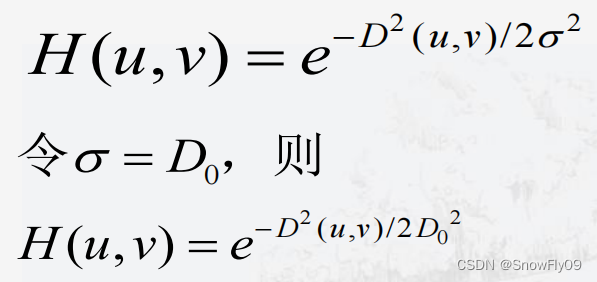
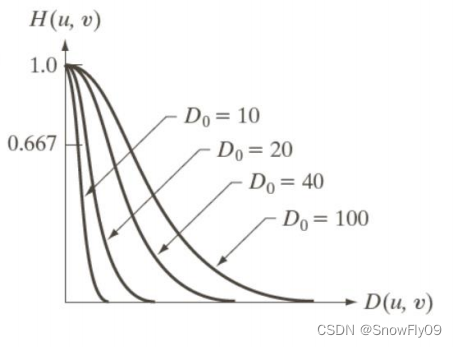
高通滤波器
同理也有理想高通滤波器,布特沃斯高通滤波器和高斯高通滤波器

相关文章:

【图像处理与机器视觉】频率域滤波
知识铺垫 复数 CRjI 可以看作复平面上的点,则该复数的坐标为(R,I) 欧拉公式 e j θ c o s θ j s i n θ e^{j\theta} cos \theta j sin \theta ejθcosθjsinθ 极坐标系中复数可以表示为: C ∣ C ∣ ( c o s…...

python第五次作业
1.请实现一个装饰器,每次调用函数时,将函数名字以及调用此函数的时间点写入文件中 # 导入datetime模块,用于获取当前时间并格式化输出 import datetime# 定义一个装饰器工厂函数log_funcName_time,它接受一个参数time def log_fu…...

JS面向对象编程
目录 实例对象与new命令this关键字对象的原型和继承Object对象的相关方法浅拷贝和深拷贝严格模式实例对象与new命令 构造函数 构造函数的特点有两个: 函数体内部使用了this关键字,代表了所要生成的对象实例。生成对象的时候,必须使用new命令。var Vehicle...

kotlin1.8.10问题导致gson报错TypeToken type argument must not contain a type variable
书接上回,https://blog.csdn.net/jzlhll123/article/details/139302991。 之前我发现gson报错后: gson在2.11.0给我的kotlin项目代码报错了。 IllegalArgumentException: TypeToken type argument must not contain a type variable 上次解释原因是因为&…...

数据库漫谈-国产数据库
国产数据库突然大量出现,下表列出(按首字母排序 ) AISWare AntDB,亚信科技。 AliSQL,阿里云。 Analyticdb,阿里云。 ArkDB,北京极数云舟科技有限公司。 CynosDB,腾讯云 DM&…...

小白跟做江科大32单片机之光敏传感器控制蜂鸣器
代码部分 1.思路 通过光敏电阻,控制蜂鸣器的发声 2.butter.h代码 #ifndef _BUTTER__H #define _BUTTER__H void butter_Init(void); void butter_on(void); void butter_off(void); #endif 3.butter.c代码 #include "stm32f10x.h" void butter…...

使用 Django Channels 构建实时聊天应用(包含用户认证和消息持久化)
文章目录 准备工作创建 Django 项目创建应用程序配置项目编写 Consumer编写路由创建 URL 路由运行应用用户认证消息持久化显示历史消息结论 Django Channels 是 Django 的一个扩展,允许在 Web 应用中添加实时功能,例如 Websockets、HTTP2 和其他协议。本…...

【Elasticsearch】es基础入门-03.RestClient操作文档
RestClient操作文档 示例: 一.初始化JavaRestClient (一)引入es的RestHighLevelClient依赖 <!--elasticsearch--> <dependency><groupId>org.elasticsearch.client</groupId><artifactId>elasticsearch-rest…...

LeetCode - 二分查找(Binary Search)算法集合(Python)[左右边界|旋转数组|双列表]
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://spike.blog.csdn.net/article/details/139419653 二分查找,也称为折半查找,是一种在有序数组中查找特定元素的高效算法。其基本原理是将待搜索的区间分成两半&am…...
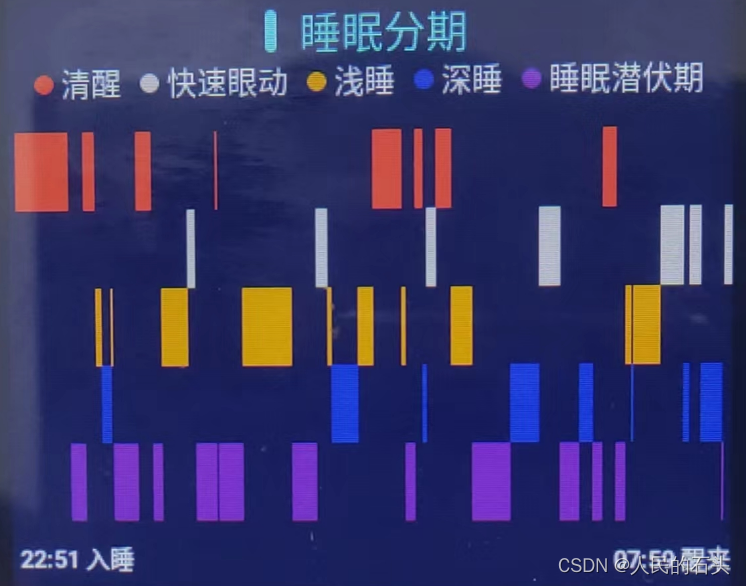
android睡眠分期图
一、效果图 做医疗类项目,经常会遇到做各种图表,本文做的睡眠分期图。 二、代码 引入用到的库 api joda-time:joda-time:2.10.1 调用代码 /*** 睡眠* 分期*/private SleepChartAdapter mAdapter;private SleepChartAttrs mAttrs;private List<SleepI…...

2023年信息素养大赛小学组C++智能算法复赛真题
今天给大家分享2023年全国青少年信息素养大赛小学组C智能算法挑战赛复赛里面的一套真题,希望有助于大家了解复赛的难度及备考。 其他真题下载:网盘-真题-信息素养大赛...
独立游戏开发的 6 个步骤
💂 个人网站:【 摸鱼游戏】【神级代码资源网站】【工具大全】🤟 一站式轻松构建小程序、Web网站、移动应用:👉注册地址🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交…...

Stable Diffusion AI绘画:从创意词汇到艺术图画的魔法之旅
文章目录 一、Stable Diffusion的工作原理二、从提示词到模型出图的过程三、Stable Diffusion在艺术创作中的应用《Stable Diffusion AI绘画从提示词到模型出图》内容简介作者简介楚天 目录前言/序言本书特色特别提示 获取方式 在科技的飞速发展中,Stable Diffusion…...

使用C++实现高效的套接字连接池
在现代网络应用中,高效管理网络连接是实现高并发和低延迟的重要因素。下面将详细介绍如何使用C实现一个高效的套接字连接池,以便在需要时快速复用连接,从而提高系统性能和资源利用率。 一、什么是连接池? 连接池是一种管理网络连…...
个人百度百科怎么创建
编辑百度词条是一个相对简单的流程,但需要注意的是,并不是所有的词条都可以编辑,部分锁定的词条是无法编辑的,但可以通过官方平台申请解封。以下百科优化网yajje分享是详细的步骤: 注册百度账号 首先,用户…...

Nvidia Jetson/Orin +FPGA+AI大算力边缘计算盒子:潍柴雷沃智慧农业无人驾驶
潍柴雷沃智慧农业科技股份有限公司,是潍柴集团重要的战略业务单元,旗下收获机械、拖拉机等业务连续多年保持行业领先,是国内少数可以为现代农业提供全程机械化整体解决方案的品牌之一。潍柴集团完成对潍柴雷沃智慧农业战略重组后,…...

ICPC训练赛补题集
ICPC训练赛补题集 文章目录 ICPC训练赛补题集D - Fast and Fat (负重越野)I-路径规划G. Inscryption(邪恶铭刻)NEW Houses雪中楼(西安交通大学)L.BracketGenerationE - Checksum D - Fast and Fat (负重越野) 原题链接:原题链接 题意:体重大的背体重小的…...
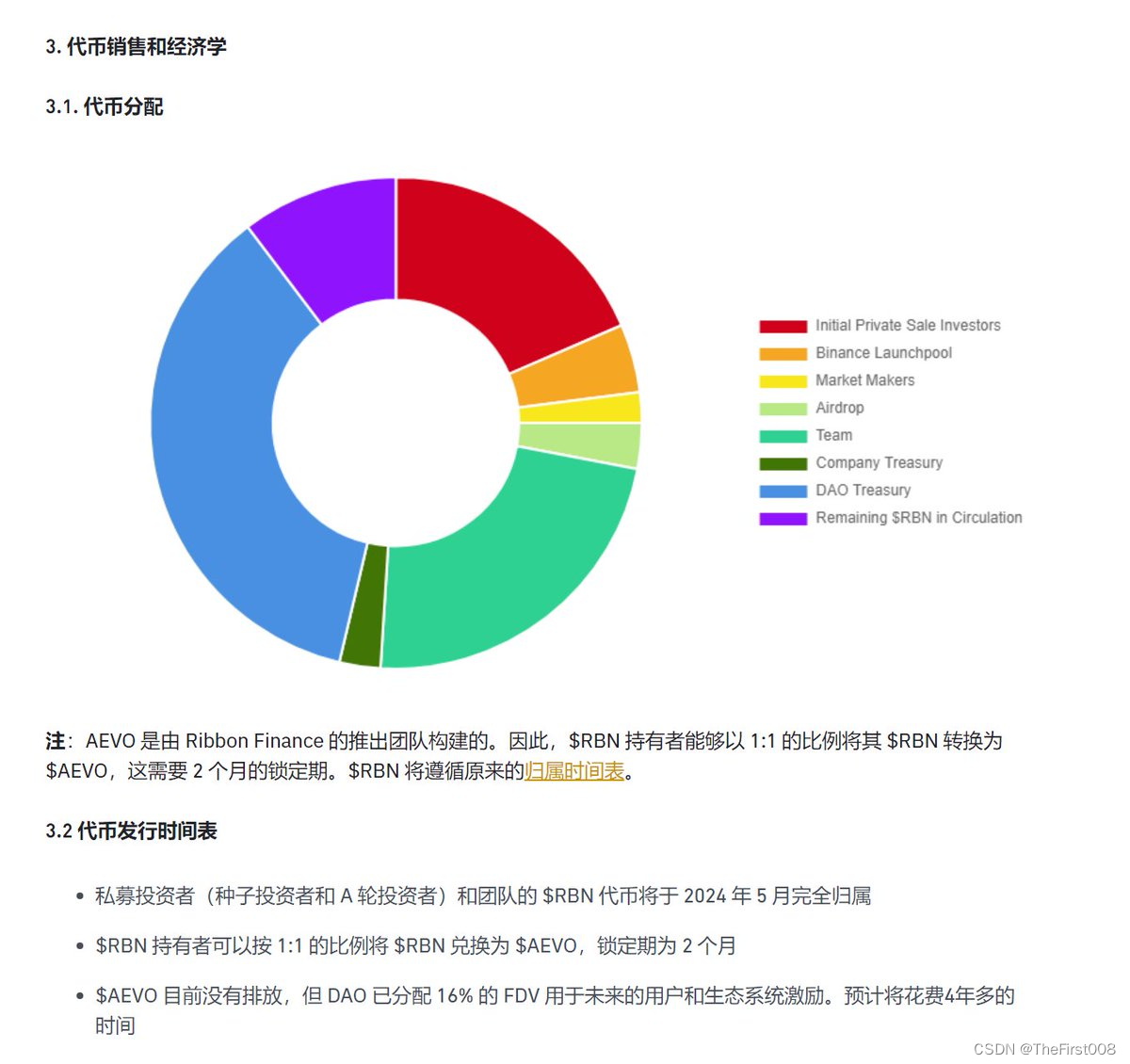
The First项目报告:解读去中心化衍生品交易所AVEO
2023 年12月8日凌晨,Solana 生态 MEV 基础设施开发商 Jito Labs 开放了 JTO 空投申领窗口,JTO 的价格在开盘短暂震荡后迅速攀高,一度触及 4.94 美元。 JTO 是加密社区这两日关注的热门标的,而在这场讨论中,除 Solana …...

Docker 快速更改容器的重启策略(Restart Policies)以及重启策略详解
目录 1. 使用 docker update 命令2. 在启动容器时指定重启策略3. 在 Docker Compose 文件中指定重启策略4. 总结 官方文档:Start containers automatically 1. 使用 docker update 命令 Docker 提供了 docker update 命令,可以在容器运行时更改其重启策…...

docker 启动关闭,设置仓库地址
1. 配置/etc/docker/daemon.json cat /etc/docker/daemon.json# 内容 {"registry-mirrors": ["https://0nth4654.mirror.aliyuncs.com"],"insecure-registries": ["harbor.domain.io"] }2. 配置systemd启动文件 和方法1配置会有冲突&a…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
