【刷题(12)】图论
一、图论问题基础
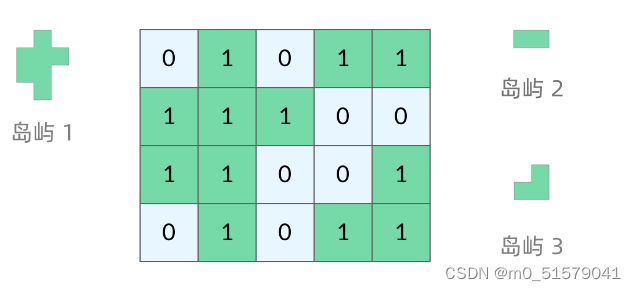
在 LeetCode 中,「岛屿问题」是一个系列系列问题,比如:
- 岛屿数量 (Easy)
- 岛屿的周长 (Easy)
- 岛屿的最大面积 (Medium)
- 最大人工岛 (Hard)
我们所熟悉的 DFS(深度优先搜索)问题通常是在树或者图结构上进行的。而我们今天要讨论的 DFS 问题,是在一种「网格」结构中进行的。岛屿问题是这类网格 DFS 问题的典型代表。网格结构遍历起来要比二叉树复杂一些,如果没有掌握一定的方法,DFS 代码容易写得冗长繁杂。
网格类问题的 DFS 遍历方法
网格问题的基本概念
我们首先明确一下岛屿问题中的网格结构是如何定义的,以方便我们后面的讨论。
网格问题是由 m×nm \times nm×n 个小方格组成一个网格,每个小方格与其上下左右四个方格认为是相邻的,要在这样的网格上进行某种搜索。
岛屿问题是一类典型的网格问题。每个格子中的数字可能是 0 或者 1。我们把数字为 0 的格子看成海洋格子,数字为 1 的格子看成陆地格子,这样相邻的陆地格子就连接成一个岛屿。
DFS 的基本结构
网格结构要比二叉树结构稍微复杂一些,它其实是一种简化版的图结构。要写好网格上的 DFS 遍历,我们首先要理解二叉树上的 DFS 遍历方法,再类比写出网格结构上的 DFS 遍历。我们写的二叉树 DFS 遍历一般是这样的:
void traverse(TreeNode root) {// 判断 base caseif (root == null) {return;}// 访问两个相邻结点:左子结点、右子结点traverse(root.left);traverse(root.right);
}
可以看到,二叉树的 DFS 有两个要素:「访问相邻结点」和「判断 base case」。
第一个要素是访问相邻结点。二叉树的相邻结点非常简单,只有左子结点和右子结点两个。二叉树本身就是一个递归定义的结构:一棵二叉树,它的左子树和右子树也是一棵二叉树。那么我们的 DFS 遍历只需要递归调用左子树和右子树即可。
第二个要素是 判断 base case。一般来说,二叉树遍历的 base case 是 root == null。这样一个条件判断其实有两个含义:一方面,这表示 root 指向的子树为空,不需要再往下遍历了。另一方面,在 root == null 的时候及时返回,可以让后面的 root.left 和 root.right 操作不会出现空指针异常。
对于网格上的 DFS,我们完全可以参考二叉树的 DFS,写出网格 DFS 的两个要素:
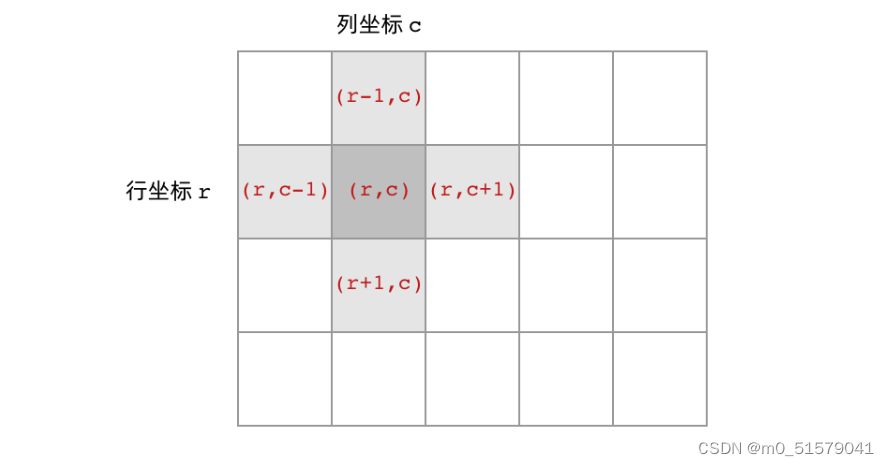
首先,网格结构中的格子有多少相邻结点?答案是上下左右四个。对于格子 (r, c) 来说(r 和 c 分别代表行坐标和列坐标),四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说,网格结构是「四叉」的。
其次,网格 DFS 中的 base case 是什么?从二叉树的 base case 对应过来,应该是网格中不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子,也就是那些超出网格范围的格子。
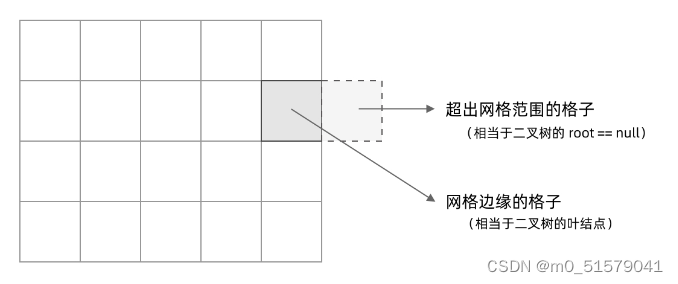
这一点稍微有些反直觉,坐标竟然可以临时超出网格的范围?这种方法我称为「先污染后治理」—— 甭管当前是在哪个格子,先往四个方向走一步再说,如果发现走出了网格范围再赶紧返回。这跟二叉树的遍历方法是一样的,先递归调用,发现 root == null 再返回。
这样,我们得到了网格 DFS 遍历的框架代码:
void dfs(int[][] grid, int r, int c) {// 判断 base case// 如果坐标 (r, c) 超出了网格范围,直接返回if (!inArea(grid, r, c)) {return;}// 访问上、下、左、右四个相邻结点dfs(grid, r - 1, c);dfs(grid, r + 1, c);dfs(grid, r, c - 1);dfs(grid, r, c + 1);
}// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}
如何避免重复遍历
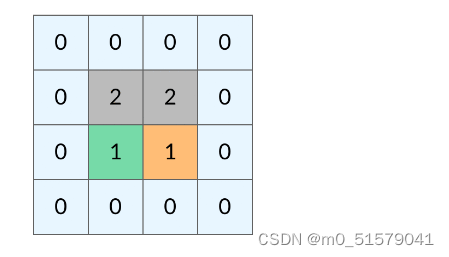
网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于,遍历中可能遇到遍历过的结点。这是因为,网格结构本质上是一个「图」,我们可以把每个格子看成图中的结点,每个结点有向上下左右的四条边。在图中遍历时,自然可能遇到重复遍历结点。
这时候,DFS 可能会不停地「兜圈子」,永远停不下来,如下图所示:
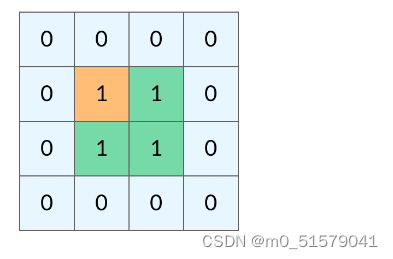
如何避免这样的重复遍历呢?答案是标记已经遍历过的格子。以岛屿问题为例,我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子,就把格子的值改为 2,这样当我们遇到 2 的时候,就知道这是遍历过的格子了。也就是说,每个格子可能取三个值:
0 —— 海洋格子
1 —— 陆地格子(未遍历过)
2 —— 陆地格子(已遍历过)
我们在框架代码中加入避免重复遍历的语句:
void dfs(int[][] grid, int r, int c) {// 判断 base caseif (!inArea(grid, r, c)) {return;}// 如果这个格子不是岛屿,直接返回if (grid[r][c] != 1) {return;}grid[r][c] = 2; // 将格子标记为「已遍历过」// 访问上、下、左、右四个相邻结点dfs(grid, r - 1, c);dfs(grid, r + 1, c);dfs(grid, r, c - 1);dfs(grid, r, c + 1);
}// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}
这样,我们就得到了一个岛屿问题、乃至各种网格问题的通用 DFS 遍历方法。以下所讲的几个例题,其实都只需要在 DFS 遍历框架上稍加修改而已。
小贴士:
在一些题解中,可能会把「已遍历过的陆地格子」标记为和海洋格子一样的 0,美其名曰「陆地沉没方法」,即遍历完一个陆地格子就让陆地「沉没」为海洋。这种方法看似很巧妙,但实际上有很大隐患,因为这样我们就无法区分「海洋格子」和「已遍历过的陆地格子」了。如果题目更复杂一点,这很容易出 bug。
二、200. 岛屿数量
1 题目

2 解题思路
(1)网格问题其实是一种特殊的四叉树,我们可以使用DFS,BFS来解这道题。
(2)使用‘2’或’0’来标记已经遍历过的陆地。
3 code
class Solution {
public:int rowCount;int colCount;int numIslands(vector<vector<char>>& grid) {this->rowCount = grid.size();this->colCount = grid[0].size();// 用来记录岛屿数量int num_islands = 0;for (int row = 0; row < rowCount; row++) {for (int col = 0; col < colCount; col++) {// 如果当前位置是岛屿的一部分if (grid[row][col] == '1') {// 岛屿数量增加num_islands++;// 从当前位置开始执行DFS, 标记整个岛屿DFS(grid, row, col);}}}return num_islands;}void DFS(vector<vector<char>>& grid, int row, int col) {// 将当前位置标记为'0', 表示已访问grid[row][col] = '2';// 检查并递归访问当前点的上下左右四个相邻点if (row - 1 >= 0 && grid[row - 1][col] == '1') DFS(grid, row - 1, col);if (row + 1 < rowCount && grid[row + 1][col] == '1') DFS(grid, row + 1, col);if (col - 1 >= 0 && grid[row][col - 1] == '1') DFS(grid, row, col - 1);if (col + 1 < colCount && grid[row][col + 1] == '1') DFS(grid, row, col + 1);}
};
三、994. 腐烂的橘子
1 题目

2 解题思路 广度优先搜索(BFS)
(1)首先分别将腐烂的橘子和新鲜的橘子保存在两个集合中;
(2)模拟广度优先搜索的过程,方法是判断在每个腐烂橘子的四个方向上是否有新鲜橘子,如果有就腐烂它。每腐烂一次时间加 111,并剔除新鲜集合里腐烂的橘子;
(3)当橘子全部腐烂时结束循环。
注:一般使用如下方法实现四个方向的移动:
# 设初始点为 (i, j)
for di, dj in [(0, 1), (0, -1), (1, 0), (-1, 0)]: # 上、下、左、右i + di, j + dj
3 code
class Solution {int dirt[4][2] = {{-1,0},{1,0},{0,1},{0,-1}};
public:int orangesRotting(vector<vector<int>>& grid) {//记录所需要腐烂的分钟int min = 0;//记录新鲜橘子的数量int fresh = 0;//记录腐烂水果坐标queue<pair<int,int>>que;//遍历地图for(int i = 0;i<grid.size();i++){for(int j = 0;j<grid[0].size();j++){if(grid[i][j]==1){fresh++;}else if (grid[i][j] ==2){que.push({i,j});}}}while(!que.empty()){int n = que.size();bool rotten = false;//遍历队列一层的元素for(int i= 0;i<n;i++){auto x = que.front(); //保存腐烂元素的坐标que.pop(); //出队列for(auto cur: dirt){int i = x.first + cur[0]; //更新x的坐标int j = x.second + cur[1]; //更新y的坐标//向四个方向遍历if(i>=0 && i<grid.size()&&j>=0&&j<grid[0].size()&&grid[i][j]==1){grid[i][j] = 2; //更新坐标que.push({i,j}); //加入队列fresh--; //新鲜数量减一rotten = true; //标记遍历完一层}}}if(rotten) min++; //遍历完一层,记录+1}return fresh ? -1:min;}
};
四、207. 课程表
1 题目

2 解题思路
(1)题目给的用例不太明显。的另外举例子。输入:3,[ [0,1] , [1,2] , [2,0] ],对于这个用例。我把图画出来。
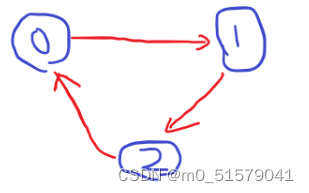
按照示例的解释是这样的:总共有 3 门课程。学习课程 2 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完成课程 1。学习课程 1 之前,你需要先完成课程 2。这是不可能的。
仔细观察就发现,这个图是有向图,并且形成了一个环。(从n点出发,最终还能回到n点),所以返回false
那这个题目就变成了:
判断有向图,是否有环。 有返回false,没有返回true
(2)那我怎么用深度优先遍历(dfs)判断有向图是否有环呢。其实很简单。
如果你写过深度优先搜索遍历。那就很简单了。
拿邻接表来解释深度优先未免有些复杂,我再画一张图
输入:4,[ [0,2], [1,0], [1,3], [3,0] ]
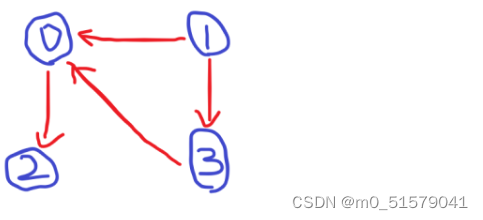
为了清晰起见,我解释一下dfs的过程。
设置一个visit数组(开节点个数),初始为0,visit =1 表示被访问过了。
我们要对每一个点进行一次深度遍历,看它是否形成环。
对 3 dfs:
visit[3]=0,3没被标记过,标记visit[3]=1, 对3进行dfs,访问和3相连接的所有点(0),
visit[0]=0,0没被标记过,标记visit[0]=1, 对0进行dfs,访问和0相连接的所有点(2),
visit[2]=0,2没被标记过,标记visit[2]=1, 对2进行dfs,访问和2相连接的所有点
(没有和2相连接的点,dfs终止,并没有环,返回true, 开始回溯)
对 2 dfs:…
对 1 dfs:…
对 0 dfs:…
回溯的时候要把visit还原为0。
递归你们都应该清楚,太麻烦就省略了,总之就是访问一个节点,就对它所有相连接的点进行dfs,这个是深度遍历的标准思路。只是加了个标记数组。
性能上的优化:我们可以在回溯的时候,把visit设置为-1,表示这个点之前已经被访问过了,走这点没环。
这样我们进入dfs后,如果visit等于 -1 ,直接返回true。
这个性能优化提速是非常明显的。虽然没优化也能通过。
3 code
class Solution {
public:vector<int>visit;bool dfs(int v,vector<vector<int>>& g){if (g[v].size() == 0) //没相邻的节点了,返回truereturn true;if (visit[v] == -1) //走这节点没环,返回truereturn true;if (visit[v] == 1) //被标记过了,存在环,返回falsereturn false;visit[v] = 1; //标记bool res = true;for (int i = 0; i < g[v].size(); i++) //访问v节点的所有相连接的节点,对于每个节点都进行dfs{res = dfs(g[v][i], g);if (res == false)break;}visit[v] =-1 ; //回溯时设置visit为-1return res;}bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {vector<vector<int>> g(numCourses);visit = vector<int>(numCourses + 1, 0);//建立有向邻接表for (int i = 0; i < prerequisites.size(); i++)g[prerequisites[i][0]].push_back(prerequisites[i][1]);bool res = true;for(int i =0;i<numCourses;i++) //对每个节的所有相连接的点进行dfs(深度优先遍历)for (int j = 0; j < g[i].size(); j++){res = dfs(g[i][j], g);if (res == false)return res;}return res;}
};
五、208. 实现Trie(前缀树)
1 题目

2 解题思路
3 code
相关文章:

【刷题(12)】图论
一、图论问题基础 在 LeetCode 中,「岛屿问题」是一个系列系列问题,比如: 岛屿数量 (Easy)岛屿的周长 (Easy)岛屿的最大面积 (Medium)最大人工岛 (Hard&…...
FASTGPT:可视化开发、运营和使用的AI原生应用
近年来,随着人工智能(AI)技术的迅猛发展,AI的应用逐渐渗透到各行各业。作为一种全新的开发模式,AI原生应用正逐步成为行业的焦点。在这方面,FASTGPT无疑是一款颇具代表性的产品。本文将详细介绍FASTGPT的设…...

代码随想录-Day27
39. 组合总和 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。 candidates 中的 同一个 数字可以 无限制重…...

TalkingData数据统计:洞察数字世界的关键工具
TalkingData数据统计:洞察数字世界的关键工具 在数字化时代,数据已成为推动社会进步和商业决策的核心动力。TalkingData作为国内领先的移动数据服务平台,为众多企业提供了全面、精准的数据统计服务。本文将深入探讨TalkingData数据统计的应用…...

printf 一次性写
PWN里printf漏洞感觉很小,可发现居然理解的不全。 一般情况下,当buf不在栈内时,就不能直接写指针。这时候需要用到rbp链或者argv链。一般操作是第一次改指针,第二次改数值。 DAS昨天这里只给了一次机会然后就exit了。今天ckyen给…...
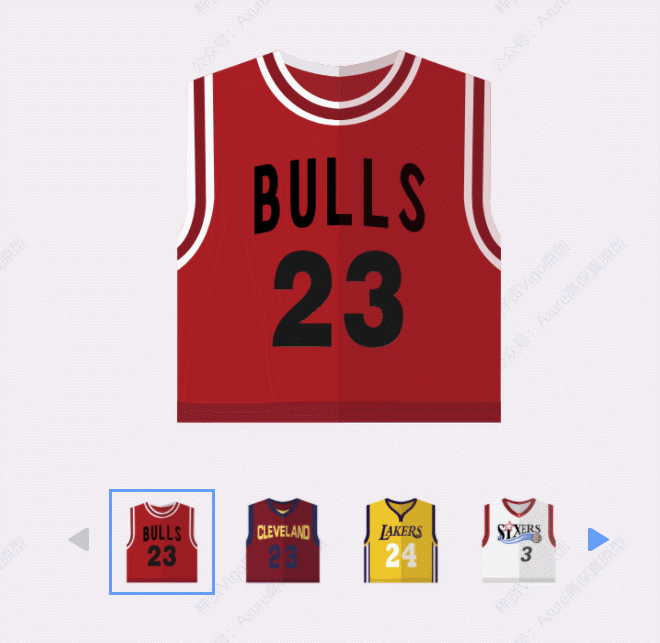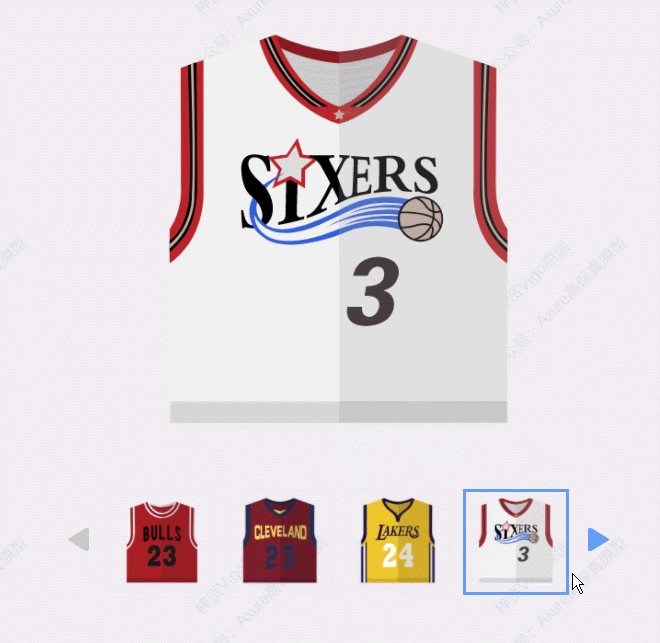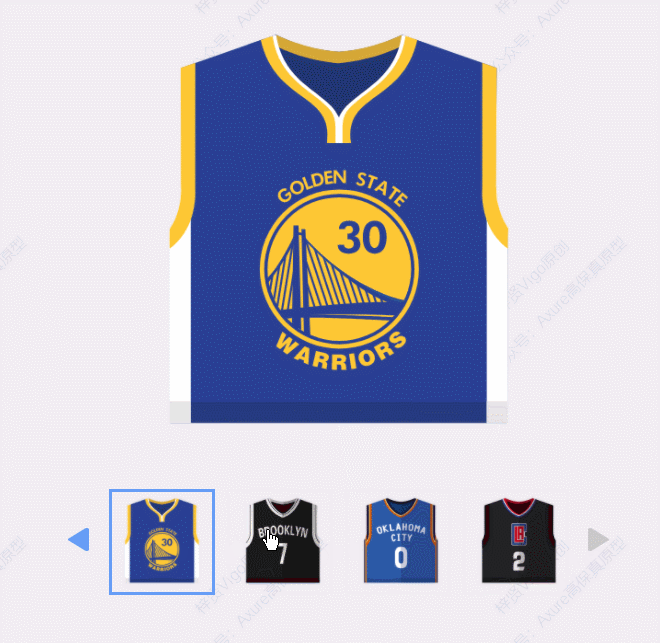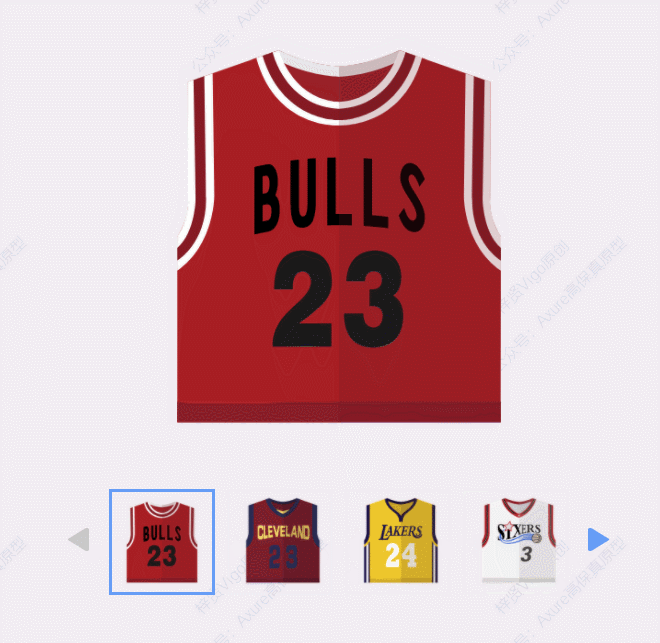
【Axure高保真原型】切换查看大图列表
今天和大家分享切换查看大图列表的原型模板,我们可以点击列表里的图片查看对应的大图,点击左右箭头可以切换切换上一页或下一页,如果是首页会自动禁用左箭头,末尾页会自动禁用右箭头。这个原型模板是用中继器制作的,所…...

Ant-Design-Vue动态表头并填充数据
Ant-Design-Vue动态表头并填充数据 Ant-Design-Vue 是一个基于 Vue.js 的前端UI框架,它继承了 Ant Design 的优秀设计理念,并针对 Vue.js 进行了深度优化。在实际开发过程中,我们经常需要处理各种复杂的表格数据,而 Ant-Design-V…...

Python-匿名函数
一、概念 匿名函数造出来的是一个内存地址,且内存地址没有绑定任何名字,很快被当做垃圾清理掉。所以匿名函数只需要临时调用一次,而有名函数永久使用; 匿名函数一般和其他函数配合使用; # 有名函数def func(x, y):…...

探索Web3工具:正确使用区块链平台工具的秘诀
在当今日新月异的数字时代,区块链技术正以惊人的速度改变着我们的生活和工作方式。尤其对于那些想要踏入区块链世界的人来说,正确使用区块链平台工具至关重要。本文将向您介绍一些关键的Web3工具,并以TestnetX.com为例,展示如何利…...
器利而事善——datagrip 的安装以及连接mysql
一,安装 下载:直接到官网下载即可, 破解:这是破解连接:https://pan.baidu.com/s/11BgOMp4Z9ddBrXwCVhwBng ,提取码:abcd; 下载后,选择倒数第三个文件,打开da…...
- 迭代器库-迭代器原语-用于指示迭代器类别的空类类型)
C++标准模板(STL)- 迭代器库-迭代器原语-用于指示迭代器类别的空类类型
迭代器库-迭代器原语 迭代器库提供了五种迭代器的定义,同时还提供了迭代器特征、适配器及相关的工具函数。 迭代器分类 迭代器共有五 (C17 前)六 (C17 起)种:遗留输入迭代器 (LegacyInputIterator) 、遗留输出迭代器 (LegacyOutputIterator) 、遗留向前…...

ClickHouse 使用技巧总结
文章目录 数据导入、导出技巧外部文件导入导技巧使用集成表引擎导入、导出数据 建表技巧表引擎选择技巧分区键选择技巧数据结构选择技巧分区技巧 高级技巧物化视图投影位图变更数据捕获 常见报错及处理方法 数据导入、导出技巧 外部文件导入导技巧 ClickHouse作为OLAP即席分析…...

论文浅尝 | THINK-ON-GRAPH:基于知识图谱的深层次且可靠的大语言模型推理方法...
笔记整理:刘佳俊,东南大学硕士,研究方向为知识图谱 链接:https://arxiv.org/pdf/2307.07697.pdf 1. 动机 本文是IDEA研究院的工作,这篇工作将知识图谱的和大语言模型推理进行了结合,在每一步图推理中利用大…...

前端科举八股文-VUE篇
前端科举八股文-VUE篇 Vue响应式的基本原理?computed和watch的区别computed和methods的区别Slot是什么 ? 作用域插槽是什么?组件缓冲keep-alive是什么? 讲讲原理v-if,v-show的区别v-modal如何实现双向绑定组件中的data属性为什么是一个函数而不是对象…...

Websocket服务端结合内网穿透发布公网实现远程访问发送信息
文章目录 1. Java 服务端demo环境2. 在pom文件引入第三包封装的netty框架maven坐标3. 创建服务端,以接口模式调用,方便外部调用4. 启动服务,出现以下信息表示启动成功,暴露端口默认99995. 创建隧道映射内网端口6. 查看状态->在线隧道,复制所创建隧道的公网地址加端口号7. 以…...
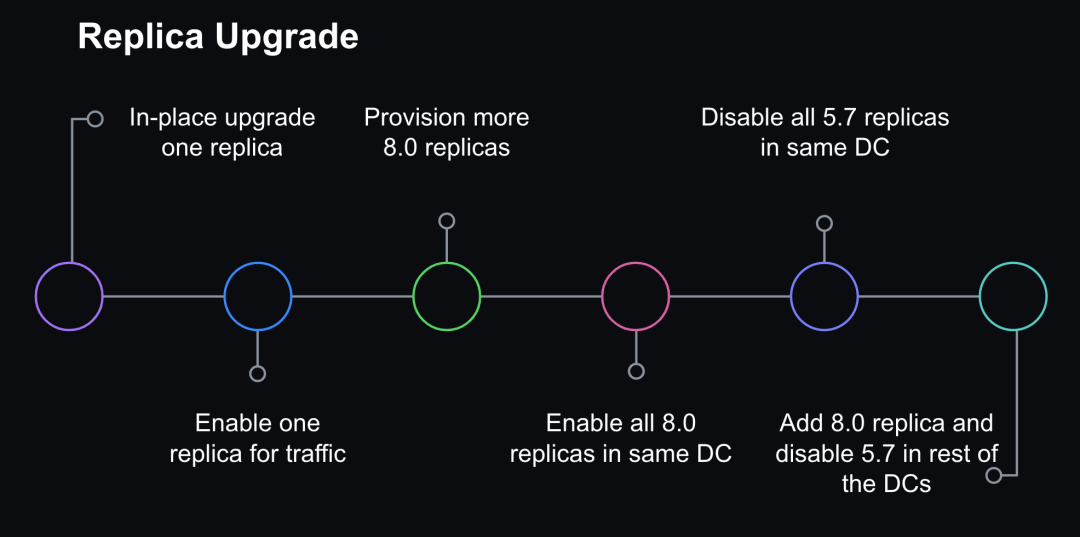
GitHub 的底层数据库从 MySQL 5.7 无缝升级到 MySQL 8.0 的实践经验
提到 MySQL 这个数据库软件,相信大家再熟悉不过了,不论是市场流行度还是占有率一直一来都非常靠前。 那再提到 MySQL 5.7 这个具体的版本,大家是不是也同样感到非常熟悉? 相信不少个人或者团队的生产环境所用的 MySQL 数据库也曾…...

概率图模型在自然语言处理中的应用
概率图模型在自然语言处理(NLP)中的应用广泛且重要,它结合了概率论和图论,为处理复杂系统中变量之间的概率依赖关系提供了有效的建模方法。以下是概率图模型在NLP中的几个主要应用,结合参考文章中的相关信息进行详细说明: 核心概念与分类: 概率图模型的核心思想是利用图…...

AI网络爬虫:对网页指定区域批量截图
对网页指定区域批量截图,可以在deepseek的代码助手中输入提示词: 你是一个Python编程专家,一步一步的思考,完成一个对网页指定区域截图的python脚本的任务,具体步骤如下: 设置User-Agent: Mozilla/5.0 (…...
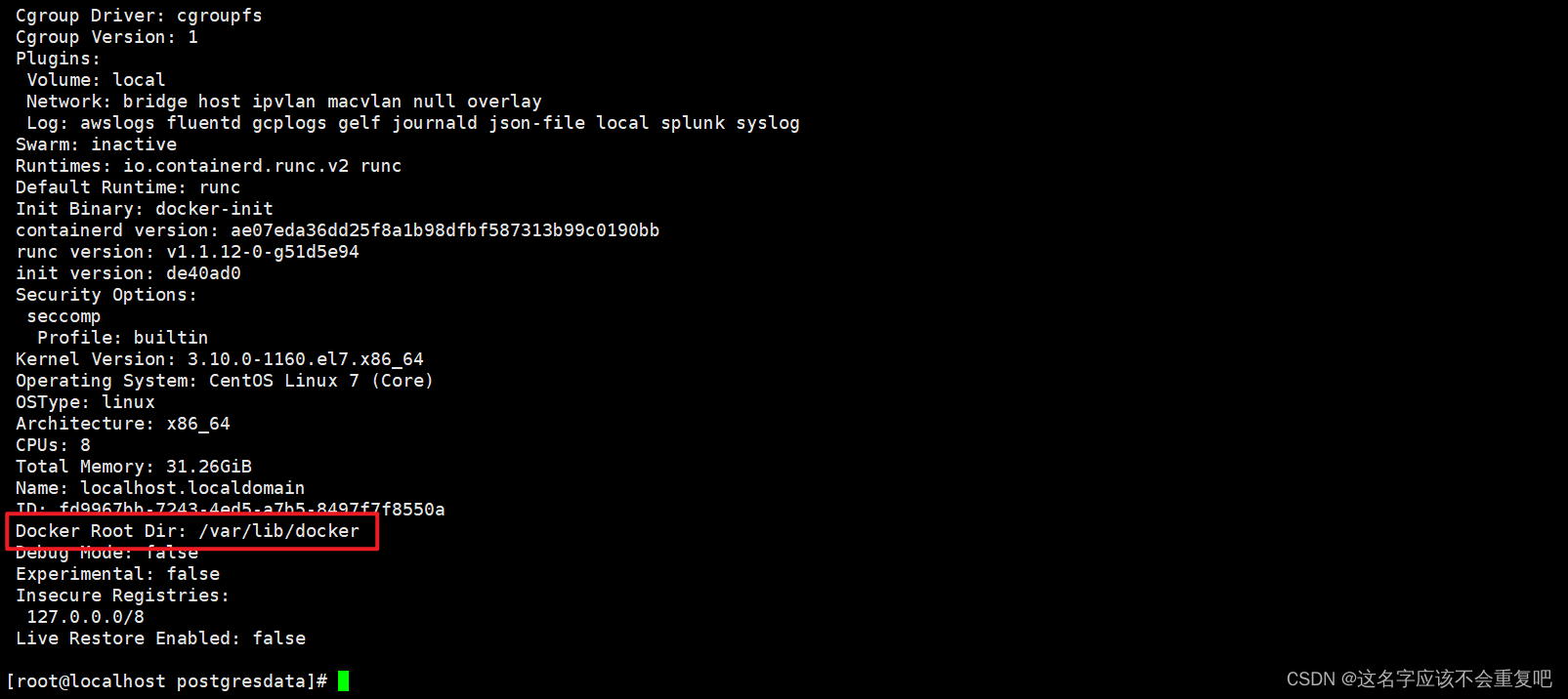
centos系统清理docker日志文件
centos系统清理docker日志文件 1.查看docker根目录位置2.清理日志 1.查看docker根目录位置 命令:docker info ,将Docker Root Dir 的值复制下来。如果目录中包含 等特殊符号的目录,需要转义 2.清理日志 创建文件:vim docker_logs_clean.…...

算法金 | Python 中有没有所谓的 main 函数?为什么?
大侠幸会,在下全网同名[算法金] 0 基础转 AI 上岸,多个算法赛 Top [日更万日,让更多人享受智能乐趣] 定义和背景 在讨论Python为何没有像C或Java那样的明确的main函数之前,让我们先理解一下什么是main函数以及它在其他编程语言…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
