C++-排序算法详解

目录

一. 冒泡排序：

二. 插入排序：

三. 快速排序：

四. 选择排序

五, 归并排序

六, 堆排序.

---

排序算法是一种将一组数据按照特定顺序（如升序或降序）进行排列的算法。

其主要目的是对一组无序的数据进行整理，使得它们呈现出一定的有序性。这样做有很多好处，比如：

• 方便查找和检索数据，提高搜索效率。
• 使数据更易于理解和分析。
• 在某些情况下，可以优化其他算法的性能。

主要排序算法有:冒泡排序.插入排序,快速排序.选择排序,归并排序,堆排序.

排序	优点	缺点
冒泡排序	简单易懂，容易实现	效率相对较低
插入排序	对于接近有序的数据效率较高	处理大规模无序数据时性能可能不太理想。
快速排序	平均性能较好，在大多数情况下效率较高	最坏情况下（比如已经有序或逆序）的性能会退化。
选择排序	算法简单直观，易于理解和实现。	它的比较次数较多，性能相对不是特别高
归并排序	具有稳定的性能，时间复杂度在最坏、平均和最好情况下都是O(nlogn)	需要额外的空间来进行合并操作
堆排序	在最坏情况下性能也较好	不太稳定。

一. 冒泡排序：

冒泡排序的优点是简单易懂，容易实现。缺点是效率相对较低，尤其是对于基本有序的数组，仍然需要进行大量的比较和交换操作。

冒泡排序是一种简单直观的排序算法。

基本原理：

• 它通过反复比较相邻的元素，如果顺序不对则进行交换，并将最大的元素逐步“冒泡”到数组的末尾。
• 经过一轮比较交换后，最大的元素就会处于正确位置，然后对剩余未排序部分重复这个过程，直到整个数组都被排序。

以下是对冒泡排序过程的详细解释：
假设要排序的数组为 arr[n]：

1. 从数组的第一个元素开始，比较相邻的元素。如果前一个元素大于后一个元素，就交换它们的位置。
2. 对整个数组进行这样的比较和交换操作，完成后，最大的元素就会“浮”到数组的末尾。
3. 忽略已经排序好的最后一个元素，对剩下的元素重复步骤 1 和 2。
4. 不断重复这个过程，直到整个数组都被排序。

以下是冒泡排序的 C++ 代码示例：

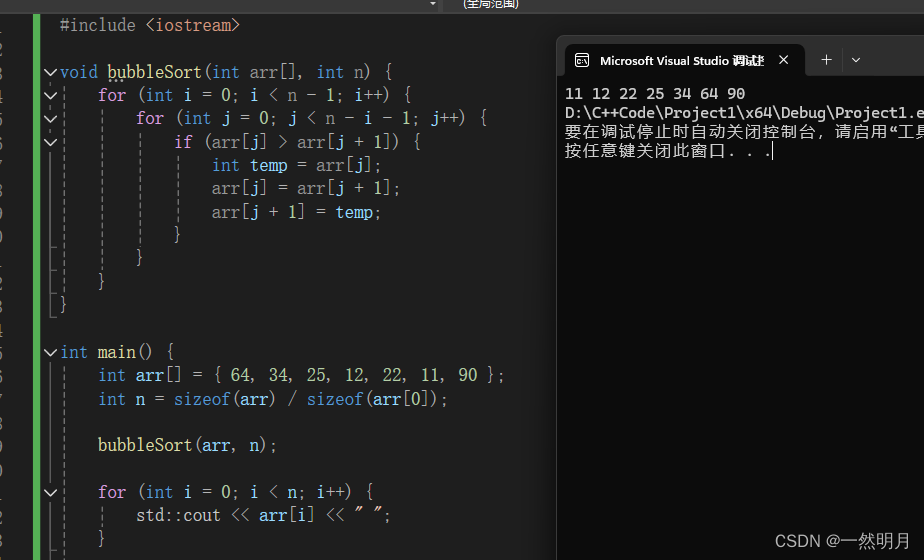
#include <iostream>void bubbleSort(int arr[], int n) {for (int i = 0; i < n - 1; i++) {for (int j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}int main() {int arr[] = {64, 34, 25, 12, 22, 11, 90};int n = sizeof(arr) / sizeof(arr[0]);bubbleSort(arr, n);for (int i = 0; i < n; i++) {std::cout << arr[i] << " ";}return 0;
}

二. 插入排序：

插入排序的优点是对于接近有序的数据效率较高，所需的比较和交换操作相对较少。缺点是在处理大规模无序数据时性能可能不太理想。

基本原理：
它逐个将元素插入到已排序的部分中，以达到整个序列有序的目的。

具体步骤如下：

1. 从第二个元素开始，将当前元素与已排序部分从后往前依次比较。
2. 如果当前元素小于比较的元素，就将比较的元素向后移动一位。
3. 一直重复这个过程，直到找到合适的位置插入当前元素。
4. 然后继续处理下一个未排序的元素，重复上述操作，直到所有元素都被插入到合适位置。

下面是插入排序的 C++ 代码示例：

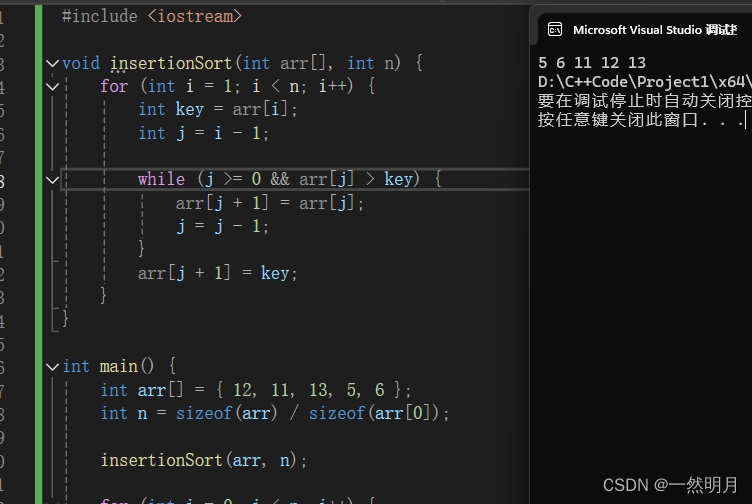
#include <iostream>void insertionSort(int arr[], int n) {for (int i = 1; i < n; i++) {int key = arr[i];int j = i - 1;while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j = j - 1;}arr[j + 1] = key;}
}int main() {int arr[] = { 12, 11, 13, 5, 6 };int n = sizeof(arr) / sizeof(arr[0]);insertionSort(arr, n);for (int i = 0; i < n; i++) {std::cout << arr[i] << " ";}return 0;
}

三. 快速排序：

快速排序的优点是平均性能较好，在大多数情况下效率较高。但它在最坏情况下（比如已经有序或逆序）的性能会退化。

基本原理：

• 选择一个基准元素。
• 将数组分为两个子数组，一个子数组中的元素都小于等于基准元素，另一个子数组中的元素都大于基准元素。
• 对这两个子数组分别进行快速排序。

具体步骤：

1. 选择数组中的一个元素作为基准（通常选择第一个或最后一个元素）。
2. 通过一趟排序将数组分为两部分，使得基准左边的元素都小于基准，右边的元素都大于基准。
3. 对基准左边和右边的子数组分别递归地进行快速排序，直到整个数组有序。

以下是一个快速排序的 C++ 代码示例：

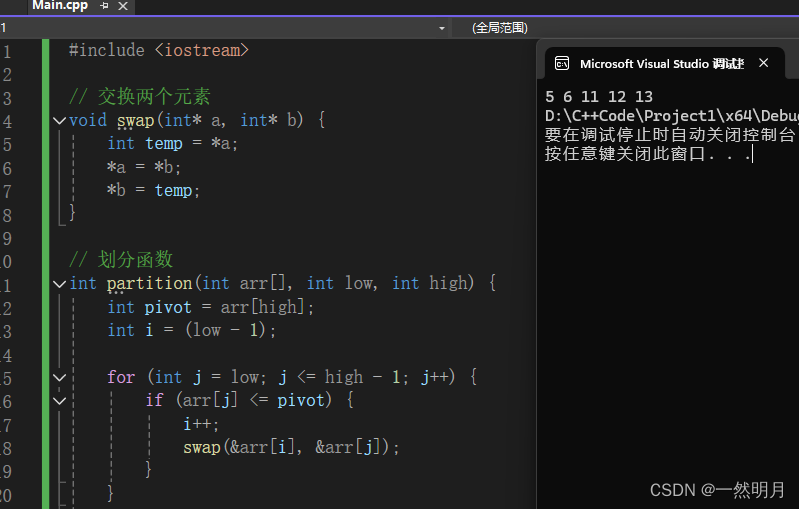
#include <iostream>// 交换两个元素
void swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;
}// 划分函数
int partition(int arr[], int low, int high) {int pivot = arr[high];int i = (low - 1);for (int j = low; j <= high - 1; j++) {if (arr[j] <= pivot) {i++;swap(&arr[i], &arr[j]);}}swap(&arr[i + 1], &arr[high]);return (i + 1);
}// 快速排序函数
void quickSort(int arr[], int low, int high) {if (low < high) {int pi = partition(arr, low, high);quickSort(arr, low, pi - 1);quickSort(arr, pi + 1, high);}
}int main() {int arr[] = { 12, 11, 13, 5, 6 };int n = sizeof(arr) / sizeof(arr[0]);quickSort(arr, 0, n - 1);for (int i = 0; i < n; i++) {std::cout << arr[i] << " ";}return 0;
}

四. 选择排序

选择排序的优点是算法简单直观，易于理解和实现。缺点是它的比较次数较多，性能相对不是特别高，尤其是对于较大规模的数据。例如，对于一个包含n个元素的数组，它需要进行大约n^2/2次比较。

基本原理：
在未排序的序列中不断地选择最小（或最大）元素，并将其放到已排序序列的末尾。

具体步骤：

1. 从整个数组的第一个元素开始，遍历所有未排序的元素，找出其中最小（或最大）的元素。
2. 将找到的最小（或最大）元素与数组的第一个未排序元素交换位置。
3. 此时第一个元素就已排序，然后从第二个未排序元素开始重复上述过程，直到整个数组都被排序。

以下是选择排序的 C++代码示例：

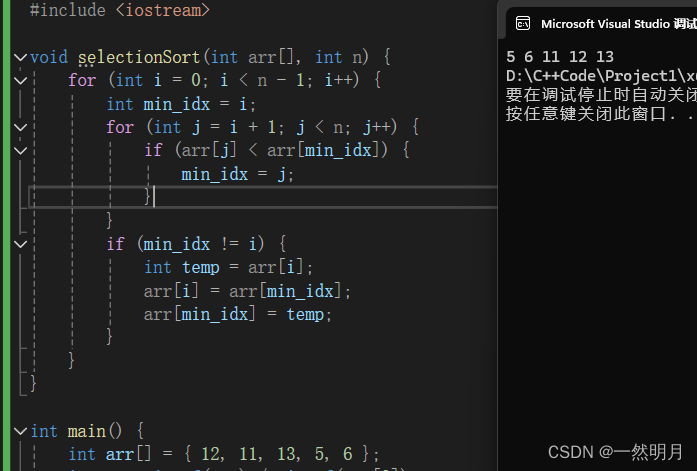
#include <iostream>void selectionSort(int arr[], int n) {for (int i = 0; i < n - 1; i++) {int min_idx = i;for (int j = i + 1; j < n; j++) {if (arr[j] < arr[min_idx]) {min_idx = j;}}if (min_idx != i) {int temp = arr[i];arr[i] = arr[min_idx];arr[min_idx] = temp;}}
}int main() {int arr[] = { 12, 11, 13, 5, 6 };int n = sizeof(arr) / sizeof(arr[0]);selectionSort(arr, n);for (int i = 0; i < n; i++) {std::cout << arr[i] << " ";}return 0;
}

五, 归并排序

归并排序的优点是具有稳定的性能，时间复杂度在最坏、平均和最好情况下都是O(nlogn)。缺点是需要额外的空间来进行合并操作。

基本原理：
将数组不断地分成两半，对每一半进行排序，然后再将排序好的两半合并起来。

具体步骤如下：

1. 把数组分成两半。
2. 对左右两部分分别递归地进行归并排序。
3. 将已经排序好的左右两部分合并为一个有序的数组。

在合并过程中，通过比较左右两部分的元素，依次将较小的元素放入新的合并后的数组中。

以下是归并排序的 C++ 代码示例：

#include <iostream>
#include <vector>// 合并函数
void merge(std::vector<int>& arr, int l, int m, int r) {int n1 = m - l + 1;int n2 = r - m;std::vector<int> left(n1), right(n2);for (int i = 0; i < n1; i++)left[i] = arr[l + i];for (int j = 0; j < n2; j++)right[j] = arr[m + 1 + j];int i = 0, j = 0, k = l;while (i < n1 && j < n2) {if (left[i] < right[j])arr[k++] = left[i++];elsearr[k++] = right[j++];}while (i < n1)arr[k++] = left[i++];while (j < n2)arr[k++] = right[j++];
}// 归并排序函数
void mergeSort(std::vector<int>& arr, int l, int r) {if (l < r) {int m = l + (r - l) / 2;mergeSort(arr, l, m);mergeSort(arr, m + 1, r);}
}int main() {std::vector<int> arr = { 12, 11, 13, 5, 6, 7, 8, 9, 10 };mergeSort(arr, 0, arr.size() - 1);for (int i = 0; i < arr.size(); i++) {std::cout << arr[i] << " ";}std::cout << std::endl;return 0;
}

六, 堆排序.

堆排序是一种选择排序。

堆排序的时间复杂度为O(n log n) ，空间复杂度为O(1) 。它的优点是在最坏情况下性能也较好，缺点是不太稳定。

基本概念：
堆是一种特殊的数据结构，可以分为大顶堆和小顶堆。大顶堆中每个节点的值都不小于其孩子节点的值，小顶堆则相反。

原理：

1. 先将数组构建成一个大顶堆。
2. 不断地将堆顶元素（最大值）与未排序部分的最后一个元素交换，然后调整堆，使其重新成为大顶堆。

具体步骤：

1. 构建大顶堆：从最后一个非叶子节点开始，依次进行调整，使每个节点及其子树都满足大顶堆的性质。
2. 排序过程：
   • 将堆顶元素和未排序部分的最后一个元素交换。
   • 对堆顶进行调整，使其重新成为大顶堆。

以下是堆排序的 C++ 代码示例：

#include <iostream>// 调整堆
void heapify(int arr[], int n, int i) {int largest = i;int l = 2 * i + 1;int r = 2 * i + 2;if (l < n && arr[l] > arr[largest])largest = l;if (r < n && arr[r] > arr[largest])largest = r;if (largest!= i) {std::swap(arr[i], arr[largest]);heapify(arr, n, largest);}
}// 堆排序函数
void heapSort(int arr[], int n) {for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);for (int i = n - 1; i > 0; i--) {std::swap(arr[0], arr[i]);heapify(arr, i, 0);}
}int main() {int arr[] = {12, 11, 13, 5, 6};int n = sizeof(arr) / sizeof(arr[0]);heapSort(arr, n);for (int i = 0; i < n; i++) {std::cout << arr[i] << " ";}return 0;
}