【数据结构】详解空间复杂度

Yan英杰的博客
悟已往之不谏 知来者之可追
目录
空间复杂度
案例1:计算BubbleSort的空间复杂度?
案例2:计算斐波那契额数列的前N项的空间复杂度
案例3:计算阶乘递归Fac的空间复杂度?
案例4:F1和F2两函数是否使用的同一块空间
案例5:计算该程序的空间复杂度
案例6:经典OJ(难度中等)
空间复杂度
 案例1:计算BubbleSort的空间复杂度?
案例1:计算BubbleSort的空间复杂度?
// 1.计算BubbleSort的空间复杂度?void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}提问:
当时我在计算该程序的空间复杂度,有个疑问,为什么不把数组算进去
这是因为,我们在计算之前,就已经开辟了数组的栈帧空间,开始前就给出了,所以不用在空间复杂度内加上数组的大小
 案例2:计算斐波那契额数列的前N项的空间复杂度
案例2:计算斐波那契额数列的前N项的空间复杂度
//计算斐波那契额数列的前N项的空间复杂度long long* Fibonacci(size_t n)
{if (n == 0)return NULL;long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n; ++i){fibArray[i] = fibArray[i - 1] + fibArray[i - 2];}return fibArray;
}分析:
我们当前的变量为0,但是我们要求第N项的空间复杂度,所以我们开辟了n+1块空间,用来计算前N项和的空间复杂度,O(N+1)为其空间复杂度,但是大O的渐进表示法,我们计算出斐波那契额数列前N项和的空间复杂度为O(N)
 案例3:计算阶乘递归Fac的空间复杂度?
案例3:计算阶乘递归Fac的空间复杂度?
//计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
 案例4:F1和F2两函数是否使用的同一块空间
案例4:F1和F2两函数是否使用的同一块空间
//F1和F2两函数是否使用的同一块空间
void F2()
{int b = 0;printf("%p\n",&b);
}
void F1()
{int a = 0;printf("%p\n",&a);
}int main()
{F1();F2();return 0;
}解析:
当调用F1函数时在Main函数低地址处进行压栈,当出了F1函数,函数销毁,同时它用过的栈帧空间返回到内存中,当我们再调用F2时,F2继续在Main函数低地址处压栈,所以他俩所维护的栈帧空间其实是同一块
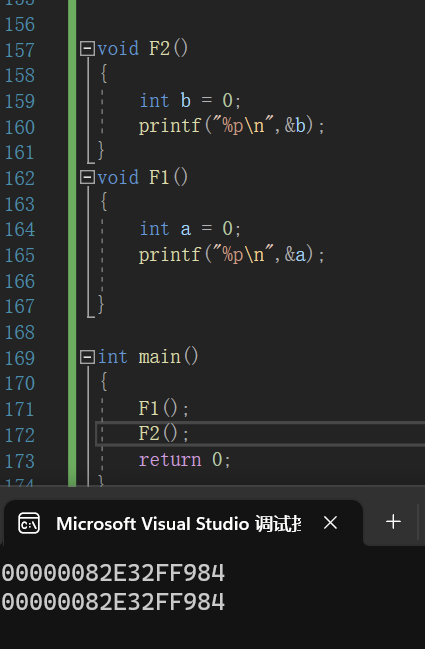
提问:
那如何修改,才能使两个函数指向不同栈帧空间?
分析:
当我们在F1中调用F2时,使得F1函数无法释放栈帧空间,F2就必须在F1低地址处压栈,此时他们两个维护的栈帧空间则不相同
图解:
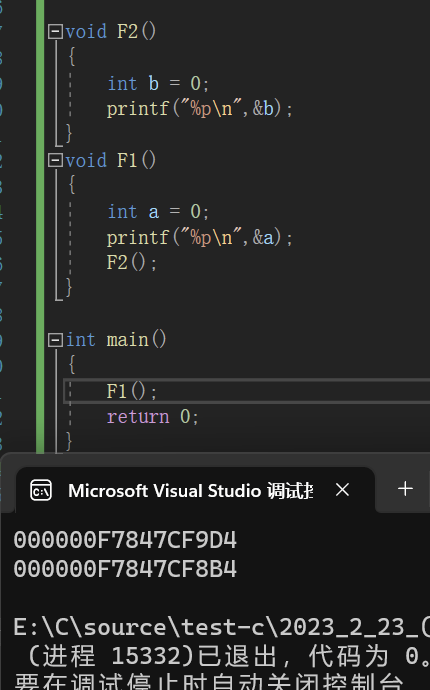
 案例5:计算该程序的空间复杂度
案例5:计算该程序的空间复杂度
//计算该程序的空间复杂度
long long Fib(size_t N)
{if (N<3){return 1;}return Fib(N-1) - Fib(N-2);
}

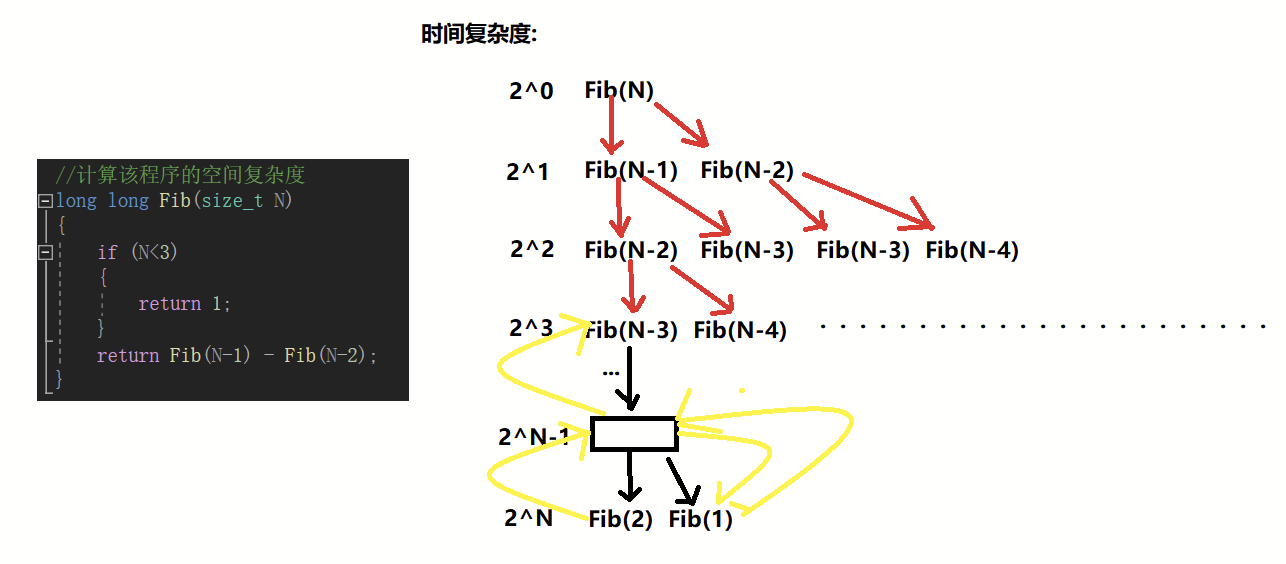
注:时间一去不复返无法重复利用,但是空间用了之后归还,可以重复利用
 案例6:经典OJ(难度中等)
案例6:经典OJ(难度中等)
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
图解:
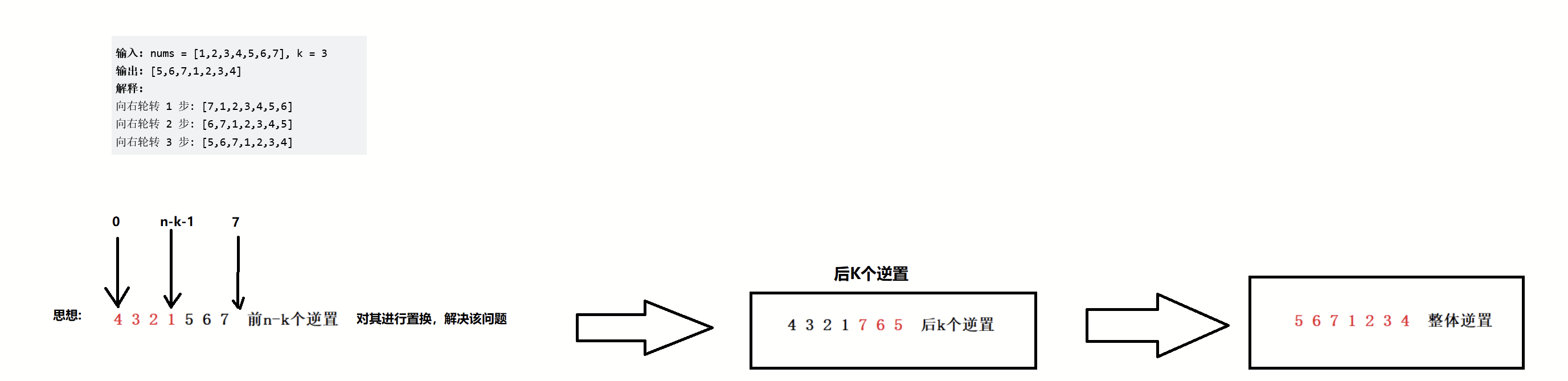
错误示范:
void reverse(int* nums,int begin ,int end) {while (begin < end){int tmp = nums[begin];nums[begin] = nums[end];nums[end] = tmp;begin++;end--;}} void rotate(int* nums, int numsSize, int k) {reverse(nums,0,numsSize-k-1);reverse(nums,numsSize-k,numsSize-1);reverse(nums, 0, numsSize - 1); }
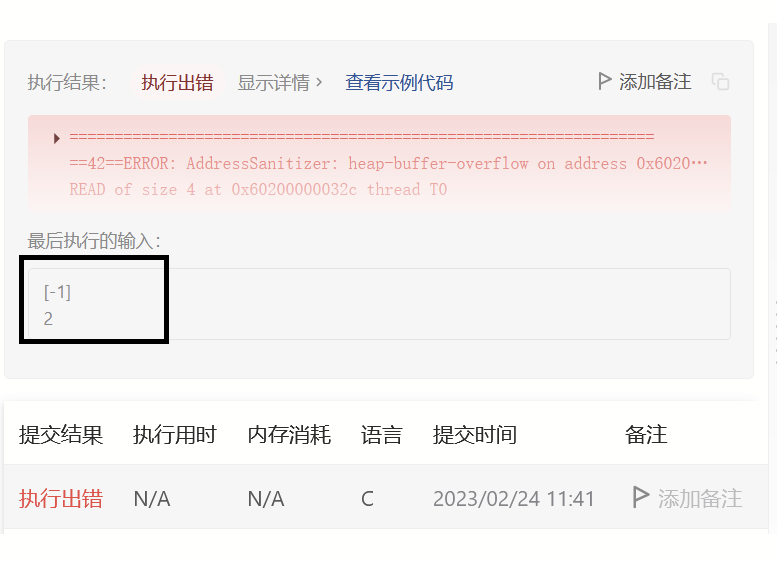
void reverse(int* nums,int begin ,int end)
{while (begin < end){int tmp = nums[begin];nums[begin] = nums[end];nums[end] = tmp;begin++;end--;}}
void rotate(int* nums, int numsSize, int k)
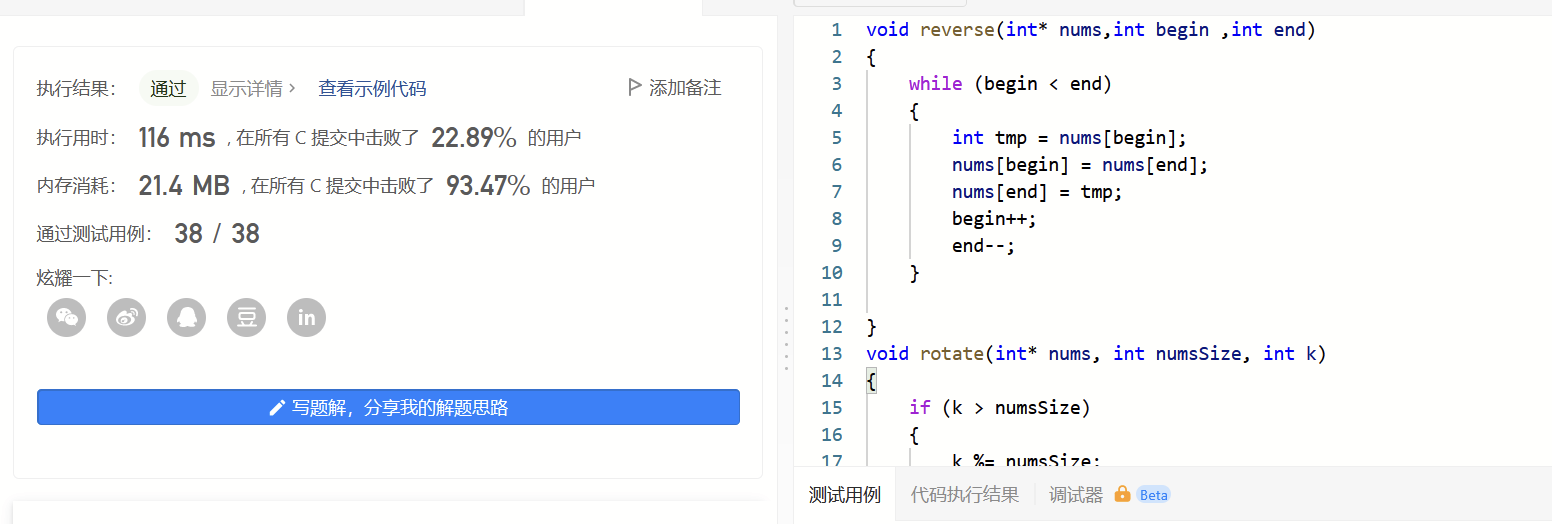
{if (k > numsSize){k %= numsSize;}reverse(nums,0,numsSize-k-1);reverse(nums,numsSize-k,numsSize-1);reverse(nums, 0, numsSize - 1);
}
相关文章:

【数据结构】详解空间复杂度
Yan英杰的博客 悟已往之不谏 知来者之可追 目录 空间复杂度 案例1:计算BubbleSort的空间复杂度? 案例2:计算斐波那契额数列的前N项的空间复杂度 案例3:计算阶乘递归Fac的空间复杂度? 案例4:F1和F2两函数是否使用的同一块空间 案例5:计算该…...
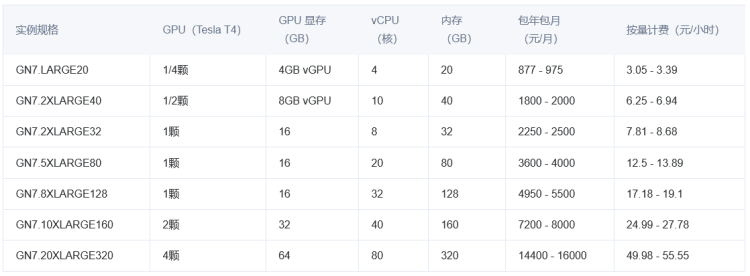
腾讯云GPU游戏服务器/云主机租用配置价格表
用于游戏业务的服务器和普通云服务器和主机空间是不同的,游戏服务器对于硬件的配置、网络带宽有更大的要求,一般游戏服务器根据不同的配置和适用场景会有十几元一小时到几十元一小时,而且可以根据不同的按量计费。而普通的云服务器可能需要几…...
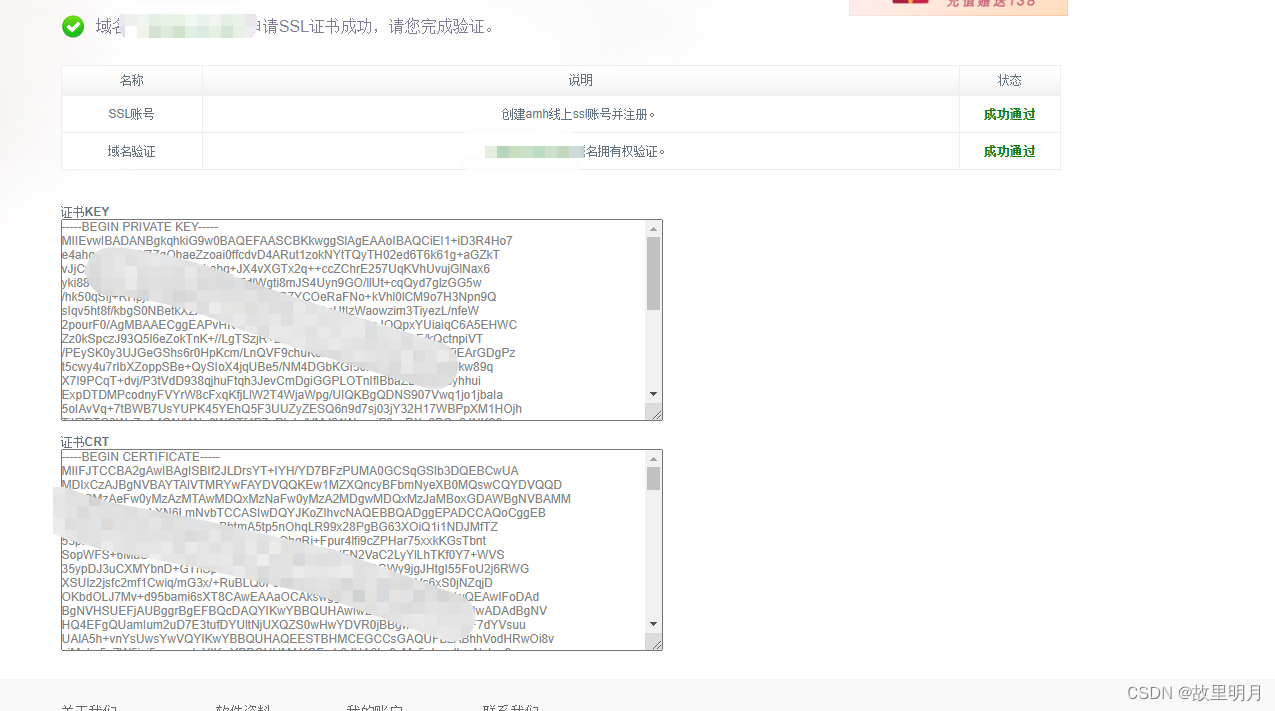
配置临时SSL子域名泛化证书
配置临时SSL子域名泛化证书 三个月有效期第一步:访问SSL证书地址第二步:在华为云上/其他服务器上搜索DNS云解析服务类似的功能第三步:将SSL申请的信息添加到服务器的记录集中第四步:添加完信息进行保存获取key / crt第五步&#x…...

【Linux:环境变量的理解】
目录 1 Z(zombie)-僵尸进程 2 孤儿进程 3 环境变量 3.1 基本概念 3.2 测试HOME 3.3 和环境变量相关的命令 3.4 环境变量的组织方式 3.5 环境变量通常是具有全局属性的 在讲环境变量之前,我们先把上次遗留知识点给总结了(僵尸进程和孤儿进程&…...

python数据类型与数据结构
目录 一、数据类型 1.1变量与常量 1.1.1变量 1.1.2常量 1.2字符串类型 1.3整数与浮点数 1.4List列表 1.5 元组tuple 1.6字典dict 二、字符串格式化 三、数据输入和类型转换 四、简单列表习题练习 一、数据类型 变量类型: 整数int(4字节&#x…...

大数据自学学习技巧?
经常有人说:先别管大数据是什么,现在理解不了没关系,先开始学,等学着学着就明白了,这种学习路线基本是混合的,很难分清楚自己学了这段怎么用在以后项目中,所以会越学越迷茫,但是等你…...

Qt音视频开发22-音频播放QAudioOutput
一、前言 以前一直以为只有Qt5以后才有QAudioOutput播放音频,其实从Qt4.6开始就有,在Qt6中变成了QAudioSink,功能一样。用QAudioOutput播放音频pcm数据极其方便,只需要指定音频播放设备(可能电脑上有多个音频输出设备…...
JavaEE简单示例——Spring的入门程序
简单介绍: 在之前我们简单的介绍了有关于Spring的基础知识,那么现在我们就来一步步的把理论融入到实践中,开始使用这个框架,使用过程也是非常的简单,大致可以分为几个基础的步骤: 1.首先引入Spring的Mave…...

【嵌入式Bluetooth应用开发笔记】第一篇:DBUS概述与蓝牙开发小试牛刀
DBUS概述 DBus(D-Bus)是一个在不同程序之间传递消息的系统总线。DBus为不同的程序之间提供了一种通信机制,这种通信制可以在不需要知道对方程序的情况下进行通信。 DBus可以使用多种编程语言来开发,包括C、C、Python、Java等。在…...
如何在电脑更换新硬盘后迁移window11系统?2种迁移方法分享!
随着时间的流逝,数据量也在逐渐增多,就会导致您的硬盘空间也变得越来越小,因此系统运行速度可能会受到一些影响而越来越慢。为了摆脱这种情况,您可以选择升级到更大的硬盘来使计算机获取更大的磁盘空间,或者迁移系统到…...

6、Elasticsearch优化
一、Elasticsearch集群配置 1、硬件选择 Elasticsearch的基础是 Lucene ,所有的索引和文档数据是存储在本地的磁盘中, 具体的路径可在 ES 的配置文件 ../config/elasticsearch.yml 中配置,如下:磁盘在现代服务器上通常都是瓶颈。…...

给力|这是一个专业的开源快速开发框架!
在低代码开发市场,专业的开源快速开发框架可以助力企业提升办公协作效率,实现提质增效的办公自动化的发展目标。 流辰信息低代码技术开发平台服务商,拥有丰富的技术经验和案例合作经验,针对不同的客户需求,提供个性化、…...

CIMCAI smart shipping company product container damage identify
世界港航人工智能领军者企业CIMCAI,领先智能航运船公司集装箱管理产品ceaspectusS™全球规模化应用落地智能化航运,全球前三船公司认可验箱标准应用。全球港航人工智能领军者企业CIMCAI,是全球第一家完成两百万次人工智能验箱,上亿…...

ego微商小程序项目-接口测试
文章目录 1.接口理论回顾1.1 接口测试相关概念1.2 接口测试流程2.接口测试文档2.1 接口测试文档基础2.2 ego微商小程序的接口文档解析3.设计接口测试用例3.1 接口测试用例基础3.2 ego微商小程序接口测试用例4. 执行测试用例4.1 ego小程序测试用例执行4.1.1 首页-轮播图4.1.2 用…...

excel文件已经损坏怎么办
1. excel文件突然损坏怎么办Excel修复不成功还可以尝试其他修复方式。1、Excel提示文件已损坏可能是受保护视图的问题。如果打开文件碰到此提示,可以先点确定。在按以下步骤操作:1)在空白程序界面,点击功能栏的【文件】࿰…...

Java【数据结构入门OJ题33道】——力扣刷题记录1
文章目录第一天存在重复元素最大子数组和第二天两数之和合并两个有序数组第三天两个数组的交集买卖股票最佳时机第四天重塑矩阵杨辉三角第五天有效的数独矩阵置零第六天字符串中第一个唯一字符救赎金第七天判断链表是否有环合并两个有序链表移除链表元素第八天反转链表删除重复…...
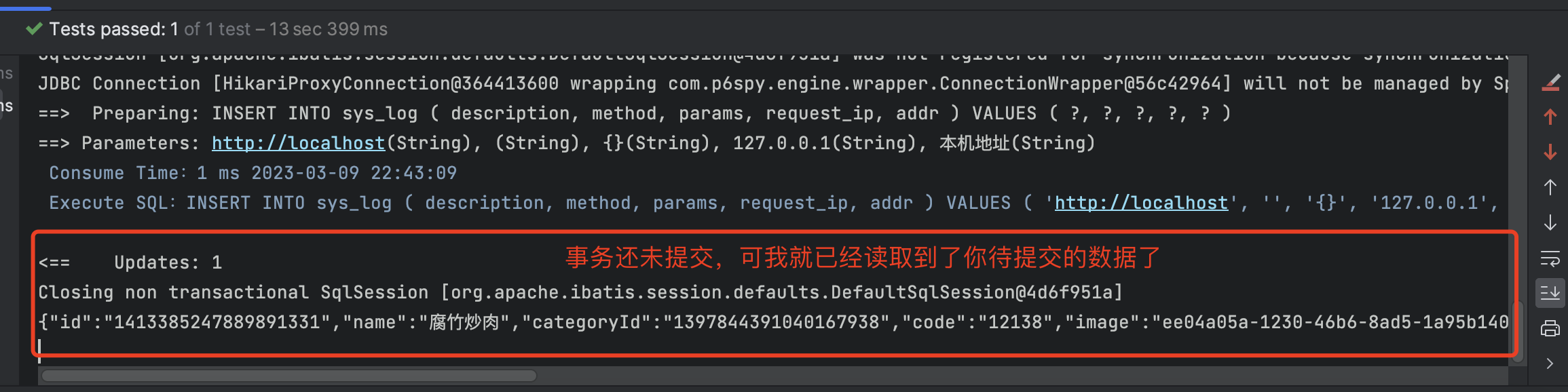
Spring事务介绍
文章目录一、编程式事务二、声明式事务(常用)三、事务实战详解3.1)事务的回滚机制3.2)事务的传播3.3)事务超时时间3.4)事务隔离级别3.5)事务回滚条件Spring中对事务有两种支持方式,分…...

Intellij Idea如何使用VM
打开Run/Debug Configuration 然后在More option 里选择 add VM options 根据要实现的目的选择main class 比如说要建造class diagram 那就选择app.ClassDiagramGenerator 然后在下面那行输入 D:\software-engineering\2023\commons-compress\target\classes true true org.apa…...

基础04-什么时候不能使用箭头函数
箭头函数的缺点 题目 什么时候不能使用箭头函数? 箭头函数的缺点 没有 arguments const fn1 () > {console.log(this, arguments) // 报错,arguments is not defined } fn1(100, 200)无法通过 call apply bind 等改变 this const fn1 () >…...
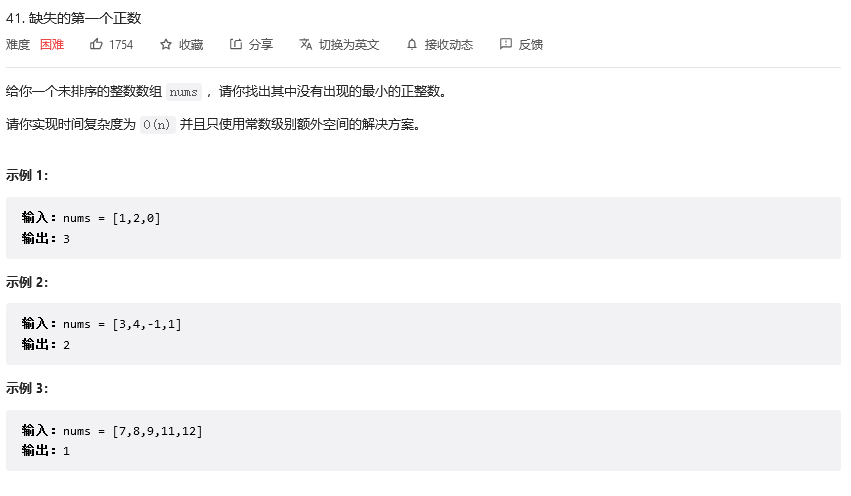
算法小抄5-原地哈希
书接上回,学会了数组中重复数字的解法三,相信接下来的题也难不倒你 找到数组中消失的数字 题目链接 题意 对于一个大小为n的数组,数组中所有的数都在[1,n]内,其中有些数字重复了,由于有些数字重复了,另一些数字就一定会确实,这次需要找到所有缺少的数字并且返回结果 有没有发…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...
