数学题目系列(一)|丑数|各位和|埃氏筛|欧拉筛
一.丑数
链接:丑数

分析:
- 丑数只有2,3,5这三个质因数,num = 2a + 3b + 5c
- 也就是一个丑数是由若干个2,3,5组成,那么丑数除以这若干个数字最后一定变为1
代码
class Solution {public boolean isUgly(int n) {if (n <= 0) return false;int[] factors = { 2, 3, 5 };for (int factor : factors)while (n % factor == 0)n /= factor;return n == 1;}
}
二.丑数II
链接:丑数II

分析
- 最容易想到的思路是暴力解法,因为在上一题中已经知道判断一个丑数的方法,但是时间复杂度太高,不能通过所有样例
暴力解法(无法通过所有样例)
class Solution {private boolean isUgly(int n) {int[] factors = {2,3,5};for(int factor : factors)while(n % factor == 0)n /= factor;return n == 1;}public int nthUglyNumber(int n) {int ret = 0, cnt = 0;for(int i = 1;;i++) {if(isUgly(i)) cnt++;if(cnt == n) return i;}}
}
- 要取出第n大的丑数,可以使用
优先级队列来存储丑数,丑数非常容易获得,就是由前一个丑数分别乘2,3,5所得 - 首先创建最小堆,堆顶元素为最小的丑数
- 初始化最小堆,堆顶元素为最小的丑数1
- 取出堆顶元素x,第几次取出就是第几大的丑数
- x是丑数,那么2x,3x,5x也都是丑数,将这三个数存储到优先级队列之中
- 在这个过程中可能会出现重复元素,可以使用哈希表来去重
- 这样,当第n次取出堆顶元素x时,x就是第n大的丑数
代码
class Solution {public int nthUglyNumber(int n) {int[] factors = {2, 3, 5};Set<Long> set = new HashSet<>();PriorityQueue<Long> q = new PriorityQueue<>();set.add(1L);q.add(1L);for(int i = 1; i < n; i++) {long top = q.poll();for(int factor : factors){long next = top * factor;if(set.add(next))q.add(next); }}return (int)q.poll().longValue();}
}
注意:
- 注意Long和long是不同的,Long是包装类,long是基本类型
- Java中,基本类型之间可以直接进行强制类型转换(int x = (int)long)
- 基本类型和其对应的包装类型在底层是通过方法进行转换的,但是在JDK5之后,编译器会自动帮助我们完成这个过程,也就是拆箱和装箱
- 包装类不能直接转换为另一个包装类或原始数据类型,必须先进行拆箱或装箱
- Long 不能直接转换为 int,因为它们是不同的类型,必须先将 Long 拆箱为 long,然后再转换为 int。
- Long转化为long是通过longvalue方法实现
三.各位相加
链接:各位相加

分析
- 模拟思路:不断获得每一位,然后计算各位和,直到最后的结果是个位数
代码
class Solution {// 求各位和private int bitSum(int n) {int ret = 0;while (n > 0) {ret += n % 10;n /= 10;}return ret;}public int addDigits(int num) {int ret = num;while(ret / 10 != 0) {ret = bitSum(ret);}return ret;}
}
数学方法
看推导:

- 核心在于:
num和其各位和 MOD9同余 - 进而推导出num和最后的结果MOD9同余
代码
class Solution {public int addDigits(int num) {if(num == 0) return 0;if(num % 9 == 0) return 9;return num % 9;}
}
四.计数质数
暴力解法(超时)
class Solution {private boolean isPrime(int n) {for(int i = 2; i <= Math.sqrt(n); i++){if(n % i == 0)return false;}return true;}public int countPrimes(int n) {int cnt = 0;for(int i = 2; i < n; i++)if(isPrime(i))cnt++;return cnt;}
}
埃氏筛
- 核心:如果x是质数,则2x,3x,4x,5x…一定不是质数
- 利用这个原理就能灵活处理很多问题
代码
class Solution {public int countPrimes(int n) {int[] is_prime = new int[n];// 标记第i个数是否是质数Arrays.fill(is_prime,1);// 默认全是质数int ret = 0;// 记录结果for(int i = 2; i < n; i++) {if(is_prime[i] == 1) {ret += 1;if((long)i*i < n)for(int k = i * i; k < n; k += i)is_prime[k] = 0;}}return ret;}
}
线性筛
- 埃氏筛其实还存在冗余的地方,比如12这个数字,被2,4,6都删除过一次,这就是冗余操作,使用线性筛可以解决这个问题
- 线性筛的核心在于:对于一个数x,x乘以小于x的所有质数的结果一定是合数,将这些结果标记为非质数即可,但是发现这样的删除过程仍然存在冗余操作,问题及解决方案如下

代码:
class Solution {public int countPrimes(int n) {List<Integer> list = new ArrayList<>();// 存储之前出现的所有质数int[] is_prime = new int[n];Arrays.fill(is_prime,1);int ret = 0;for(int i = 2; i < n; i++) {if(is_prime[i] == 1){list.add(i);ret++;}for(int k : list){if(k*i >= n) break;is_prime[k*i] = 0;if(i % k == 0) break;// k是i的最小质因数}}return ret;}
}
三种算法的时间复杂度对比(数据量大)
- 线性筛 > 埃氏筛 > 暴力解法
对比实验:求2-n之间所有的质数
代码:
package org.example;import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;// 打印2-n之间的所有质数
public class Demo2 {// 埃氏筛public static void Eratosthenes(int n) {List<Integer> list = new ArrayList<>();int[] is_prime = new int[n + 1];Arrays.fill(is_prime, 1);for(int i = 2; i <= n; i++) {if(is_prime[i] == 1){list.add(i);if((long)i*i <= n)for(int k = i*i; k <= n; k += i)is_prime[k] = 0;}}}// 暴力解法public static void isPrime(int n){List<Integer> list = new ArrayList<>();for(int i = 2; i<= n; i++){if(is_prime(i))list.add(i);}}private static boolean is_prime(int n){for(int i = 2; i <= Math.sqrt(n); i++)if(n % i == 0)return false;return true;}// 线性筛public static void Euler_prime(int n){List<Integer> list = new ArrayList<>();int[] is_prime = new int[n + 1];Arrays.fill(is_prime, 1);for(int i = 2; i <= n; i++) {if(is_prime[i] == 1)list.add(i);for(int k : list){if(k*i > n) break;is_prime[k*i] = 0;if(i % k == 0) break;// k是i的最小质因数}}}public static void main(String[] args) {int n = 200000000;long start1 = System.currentTimeMillis();Eratosthenes(n);long end1 = System.currentTimeMillis();System.out.println("埃氏筛时间:" + (end1 - start1));long start2 = System.currentTimeMillis();isPrime(n);long end2 = System.currentTimeMillis();System.out.println("暴力时间:" + (end2 - start2));long start3 = System.currentTimeMillis();Euler_prime(n);long end3 = System.currentTimeMillis();System.out.println("线性筛时间:" + (end3 - start3));}
}打印结果:

- 只有当数据量特别大时,才符合上述时间复杂度的排序,对于计算机来说,取模%是一个非常耗时的操作
相关文章:

数学题目系列(一)|丑数|各位和|埃氏筛|欧拉筛
一.丑数 链接:丑数 分析: 丑数只有2,3,5这三个质因数,num 2a 3b 5c也就是一个丑数是由若干个2,3,5组成,那么丑数除以这若干个数字最后一定变为1 代码 class Solution {publi…...

k8s学习--Secret详细解释与应用
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 Secret什么是Secret?Secret四种类型及其特点Secret应用案例(1)将明文密码进行base64编码(2)编写创建secret的YAML文…...

功能问题:如何防止接口重复请求?
大家好,我是大澈! 本文约 1400 字,整篇阅读约需 3 分钟。 防止接口重复请求在软件开发中非常重要,重复请求必然会导致服务器资源的浪费。 因为每次请求都需要服务器进行处理,如果请求是重复的,那么服务…...
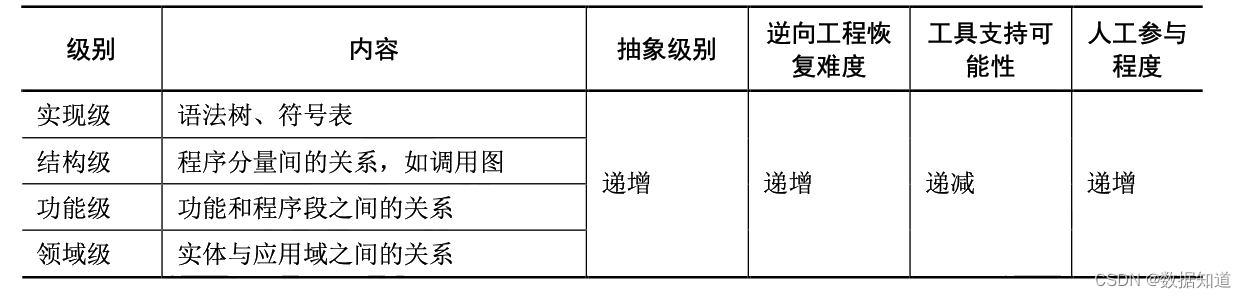
系统架构设计师【第5章】: 软件工程基础知识 (核心总结)
文章目录 5.1 软件工程5.1.1 软件工程定义5.1.2 软件过程模型5.1.3 敏捷模型5.1.4 统一过程模型(RUP)5.1.5 软件能力成熟度模型 5.2 需求工程5.2.1 需求获取5.2.2 需求变更5.2.3 需求追踪 5.3 系统分析与设计5.3.1 结构化方法5.3.2 面向对象…...

嵌入式Linux系统编程 — 2.2 标准I/O库:检查或复位状态
目录 1 检查或复位状态简介 2 feof()函数 2.1 feof()函数简介 2.2 示例程序 3 ferror()函数 4 clearerr()函数 4.1 clearerr()函数简介 4.2 示例程序 1 检查或复位状态简介 调用 fread() 函数读取数据时,如果返回值小于参数 nmemb 所指定的值,这…...
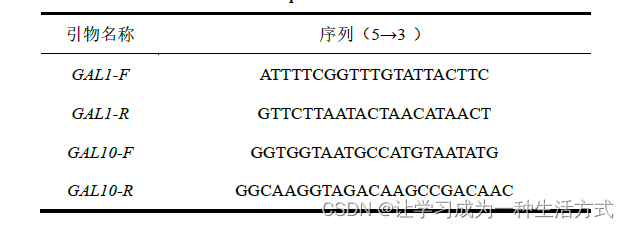
pESC-HIS是什么,怎么看?-实验操作系列-2
01 典型的pESC-HIS质粒遗传图谱 02 介绍 质粒类型:酿酒酵母蛋白表达载体 表达水平:高拷贝 诱导方法:半乳糖 启动子:GAL1和GAL10 克隆方法:多克隆位点,限制性内切酶 载体大小:6706bp 5 测…...
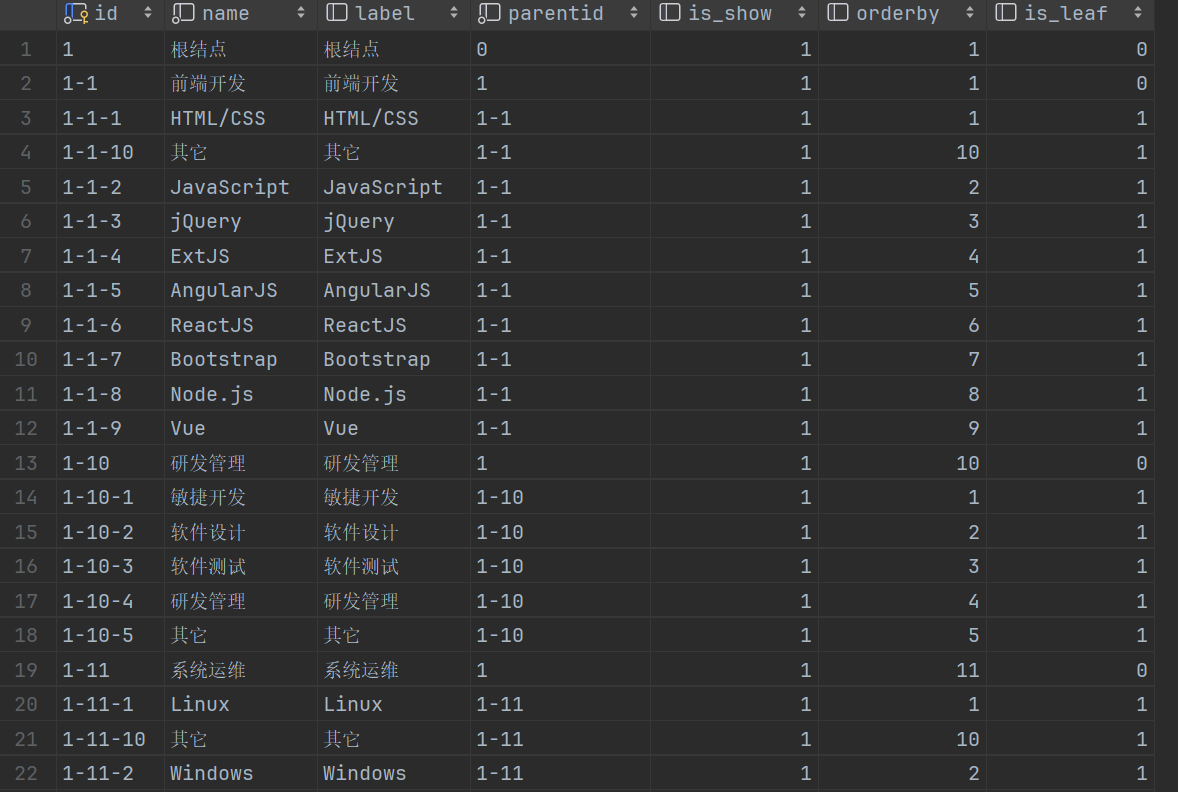
树形表/树形数据接口的开发
数据表格式 需要返回的json格式 点击查看json数据 [{"childrenTreeNodes" : [{"childrenTreeNodes" : null,"id" : "1-1-1","isLeaf" : null,"isShow" : null,"label" : "HTML/CSS","na…...

二叉树的镜像--c++【做题记录】
【问题描述】 给定扩展二叉树的前序序列,构建二叉树。 求这课二叉树的镜像,并输出其前序遍历序列。 【输入形式】 输入扩展二叉树的前序序列。 【输出形式】 输出镜像二叉树的前序遍历序列。 【样例输入】 ab##cd##e## 【样例输出】 镜像后二叉树的前序遍…...
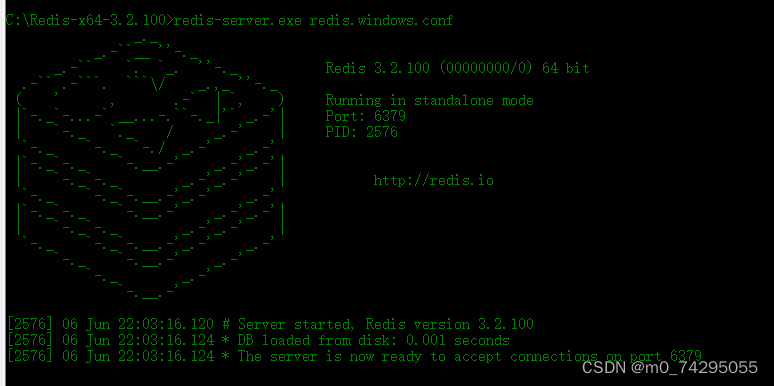
redis安裝启动
1、下载redis解压 https://github.com/tporadowski/redis/releases 2、打开cmd,切换到解压的文件夹 3、redis-server.exe redis.windows.conf 启动redis redis可通过命令行输入config set requirepass password和直接修改redis.config文件中修改 requirepass 来设…...

为什么Java中的main方法必须是public static void的?
当我们创建main方法时,首先都是public、都是static,返回值都是void,方法名都是main,入参都是一个字符串数组。 在以上的方法声明中,唯一可以改变的部分就是方法的参数名,我们可以吧args改成任意我们想要使…...
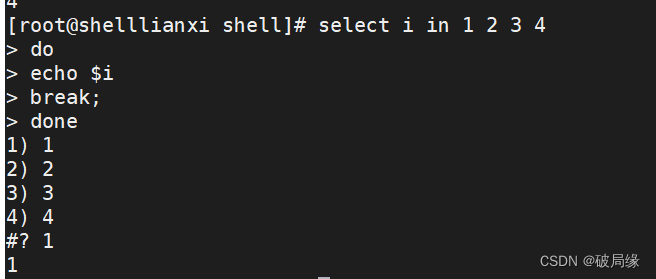
shell的编程方式
文章目录 变量俩种方式第一种方式第二种方式 取消变量数组创建数组获取数组元素的方式 read输出的方式限制输入的方式 流程控制方式for循环输出的方式第一种方式第二种方式while循环输出的方式select选择输出的方式 判断方式判断的四种方式第一种方式第二种方式第三种方式 算术…...
前端面试项目细节重难点(已工作|做分享)想(八)
面试官:请你讲讲你在该项目中遇到的印象深刻的问题是什么? 答:我的回答:该项目的实现过程中我确实遇到了问题:【我会给大家整理回答思路和角度,那那么遇到这样的问题也可借鉴这种思路进行阐述】 第一层面…...

Loguru,一个 Python 日志神器
大家好!我是爱摸鱼的小鸿,关注我,收看每期的编程干货。 一个简单的库,也许能够开启我们的智慧之门, 一个普通的方法,也许能在危急时刻挽救我们于水深火热, 一个新颖的思维方式,也许能激发我们无尽的创造力, 一个独特的技巧,也许能成为我们的隐形盾牌…… 神奇的 Pyth…...

C++ 反转单词
在C中,反转一个字符串中的单词(单词之间通过空格分隔,但单词内部保持原有顺序)可以通过以下步骤实现: 找到字符串中的所有单词,这可以通过查找空格来实现。将单词存储在一个容器中(例如 std::v…...

Apache Doris 基础 -- 数据表设计(表索引)
1、索引概述 索引用于帮助快速过滤或搜索数据。目前,Doris支持两种类型的索引:内置智能索引和用户创建的二级索引。 内置智能索引 排序键和前缀索引:Apache Doris基于排序键以有序的方式存储数据。它为每1024行数据创建一个前缀索引。索引中的键是当前1024行组的…...

资源描述框架的用途及实际应用解析
什么是RDF? RDF代表 资源描述框架 RDF是用于描述网络资源的框架 RDF旨在被计算机阅读和理解 RDF并非设计用于供人阅读 RDF以 XML 编写 示例 描述购物商品的属性,如价格和可用性描述网络活动的时间表描述网页的信息(内容,作者&a…...

工业级物联网边缘网关解决方案-天拓四方
随着工业4.0时代的到来,越来越多的企业开始寻求智能化升级,以提高生产效率、降低运营成本并增强市场竞争力。然而,在实际的转型升级过程中,许多企业面临着数据孤岛、设备兼容性差、网络安全风险高等问题,这些问题严重制…...

认识微服务,认识Spring Cloud
1. 介绍 本博客探讨的内容如下所示 什么是微服务?什么是springcloud?微服务和springcloud有什么关系? 首先,没有在接触springcloud之前,我写的项目都是单体结构, 但随着网站的用户量越来越大,…...
电脑设置密码怎么设置?让你的电脑更安全!
在如今信息化的社会中,保护个人电脑的安全至关重要。设置密码是最基本的电脑安全措施之一,它可以有效防止未经授权的访问和保护个人隐私,可是电脑设置密码怎么设置?本文将介绍三种设置电脑密码的方法,帮助您加强电脑的…...

搜维尔科技:SenseGlove Nova2使用主动接触反馈来模拟手掌的感觉,结合力反馈和振动触觉反馈,使其成为市场上第一款具有手掌反馈的无线触觉手套
SenseGlove Nova2使用主动接触反馈来模拟手掌的感觉,结合力反馈和振动触觉反馈,使其成为市场上第一款具有手掌反馈的无线触觉手套。 搜维尔科技:SenseGlove Nova2使用主动接触反馈来模拟手掌的感觉,结合力反馈和振动触觉反馈&…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
