VOJ 迷阵突围 题解 次短路径 dijkstra算法
迷阵突围
题目描述
小明陷入了坐标系上的一个迷阵,迷阵上有 n 个点,编号从 1 到 n 。小明在编号为 1 的位置,他想到编号为 n 的位置上。小明当然想尽快到达目的地,但是他觉得最短的路径可能有风险,所以他会选择第二短的路径。现在小明知道了 n 个点的坐标,以及哪些点之间是相连的,他想知道第二短的路径长度是多少。
注意,每条路径上不能重复经过同一个点。
输入描述
第一行输入两个整数 n ( 1 ≤ n ≤ 200 1 ≤ n ≤ 200 1≤n≤200 ) 和 m ,表示一共有 n 个点和 m 条边。
接下来输入 n 行,每行输入两个整数 x i x_i xi, y i y_i yi( − 500 ≤ x i −500 ≤ x_i −500≤xi, y i ≤ 500 y_i ≤ 500 yi≤500 ),代表第 i i i 个点的坐标。
接下来输入 m 行,每行输入两个整数 p j p_j pj, q j q_j qj( 1 ≤ p j 1 ≤ p_j 1≤pj, q j ≤ n q_j ≤ n qj≤n ),表示点 p j p_j pj 和点 q j q_j qj 之间相连。
输出描述
输出一行,输出包含一个数,表示第二短的路径长度(小数点后面保留两位),如果第一短路径有多条,则答案就是第一最短路径的长度;如果第二最短路径不存在,则输出 −1 。
样例 #1
样例输入 #1
3 3
1 1
2 2
3 2
1 2
2 3
1 3
样例输出 #1
2.41
思路
求次短路径长度分为两种:一种是可以重复经过一个点的,另一种是不能重复经过一个点的。前者解题策略是用dis1和dis2分别记录最短路长度和次短路长度,并在更新过程中依次判断是否需要更新最短路和次短路;后者解题策略是先统计出最短路径所经过的所有边,然后枚举所有经过的边,在去掉该边的情况下重新求出最短路径长度,并用ans记录重新求出的n个新图上最短路径长度中最小的那个,即为原图上的次短路径长度。对于本题,题目明确说明属于后者。注意,当最短路径不存在时,需要特判,此时次短路径一定不存在,输出 -1。
代码
#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
typedef long long ll;const int maxn = 1e5 + 6;
const int maxm = 1e5 + 6;struct edge
{int to; // to为边的指向double len; // len为边的长度即边权
};vector<edge> e[maxn]; // 存储以点i为起点的边struct node
{double dis; // dis为目前到该点的最短路长度int num; // num为该点序号bool operator>(const node &a) const // 小根堆中的大于号重载{return dis > a.dis;}
};double minDis[maxn]; // 从起点到第i个点的最短路长度
bool vis[maxn]; // 第i个点是否已确定最短路长度
int pre[maxn];
int x, y; // 记录去掉的边的起点x和终点yvoid dijkstra(int n, int s) // n为点的个数,s为起点
{priority_queue<node, vector<node>, greater<node>> pq; // 还未确定最短路长度的点存放在小根堆中// 将最短路距离初始化为无穷大,vis初始化为0for (int i = 1; i <= n; i++){minDis[i] = 1e10;vis[i] = 0;}minDis[s] = 0.0; // 起点到起点的最短路长度为0pq.push({0, s});while (!pq.empty()){int u = pq.top().num; // 有向边的起点pq.pop();if (vis[u]) // 若该点已确定最短路长度,跳过continue;vis[u] = 1;for (edge eg : e[u]) // 遍历以该点为起点的所有有向边{int v = eg.to;if (x == u && y == v) // 遍历到去掉的边就跳过,从而找到次短路径continue;double w = eg.len;if (minDis[v] > minDis[u] + w) // 更新最短路长度{minDis[v] = minDis[u] + w;pre[v] = u; // 用pre记录最短路径中v的前驱upq.push({minDis[v], v});}}}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);// 问题转化为求根1到各个结点的最短路径长度int n, m, s; // 点的个数,有向边的个数,出发点的编号cin >> n >> m;vector<pair<int, int>> a(n + 1); // 点的坐标for (int i = 1; i <= n; i++){cin >> a[i].first >> a[i].second;pre[i] = i;}s = 1; // 起点为根结点int u, v;double w;while (m--){cin >> u >> v;// 在读入无向边的过程中计算每条边的边权,即两点间距离w = sqrt(pow((a[u].first - a[v].first), 2) + pow((a[u].second - a[v].second), 2));e[u].push_back({v, w});e[v].push_back({u, w});}dijkstra(n, s);if (pre[n] == n) // 如果不存在最短路径,那么一定不存在次短路径{cout << -1 << '\n';return 0;}vector<pair<int, int>> path;int tmp = n;while (tmp != 1) // 通过从n向1遍历前驱,即可找出完整的路径{path.push_back({pre[tmp], tmp});tmp = pre[tmp];}double ans = 1e10;for (int i = 0; i < path.size(); i++) // 枚举路径上所有的边,统计去掉该边后的新图上最短路径长度的最小值{x = path[i].first;y = path[i].second;dijkstra(n, s);ans = min(ans, minDis[n]);}if (ans == 1e10) // 如果不存在次短路径,输出-1{cout << -1 << '\n';}else{cout << fixed << setprecision(2) << ans << '\n';}return 0;
}
相关文章:

VOJ 迷阵突围 题解 次短路径 dijkstra算法
迷阵突围 题目描述 小明陷入了坐标系上的一个迷阵,迷阵上有 n 个点,编号从 1 到 n 。小明在编号为 1 的位置,他想到编号为 n 的位置上。小明当然想尽快到达目的地,但是他觉得最短的路径可能有风险,所以他会选择第二短…...

Oracle SQL详解
Oracle SQL是一种用于管理和操作Oracle数据库的编程语言。以下是一些基本的Oracle SQL语法和建表建用户的详解。 创建用户 在Oracle中,创建用户通常需要具有足够权限的用户(通常是具有DBA角色的用户)。以下是一个创建用户的例子:…...

产业,到底需要什么大模型?
[ 产业究竟需要怎样的大模型?关于这个问题,本文作者便提出了他的看法,并总结了产业大模型目前阶段的三点落地挑战。一起来看看,或许可以帮助你更好地理解大模型与行业、与产业的融合。 写下这篇的起因,是前不久的一件事…...
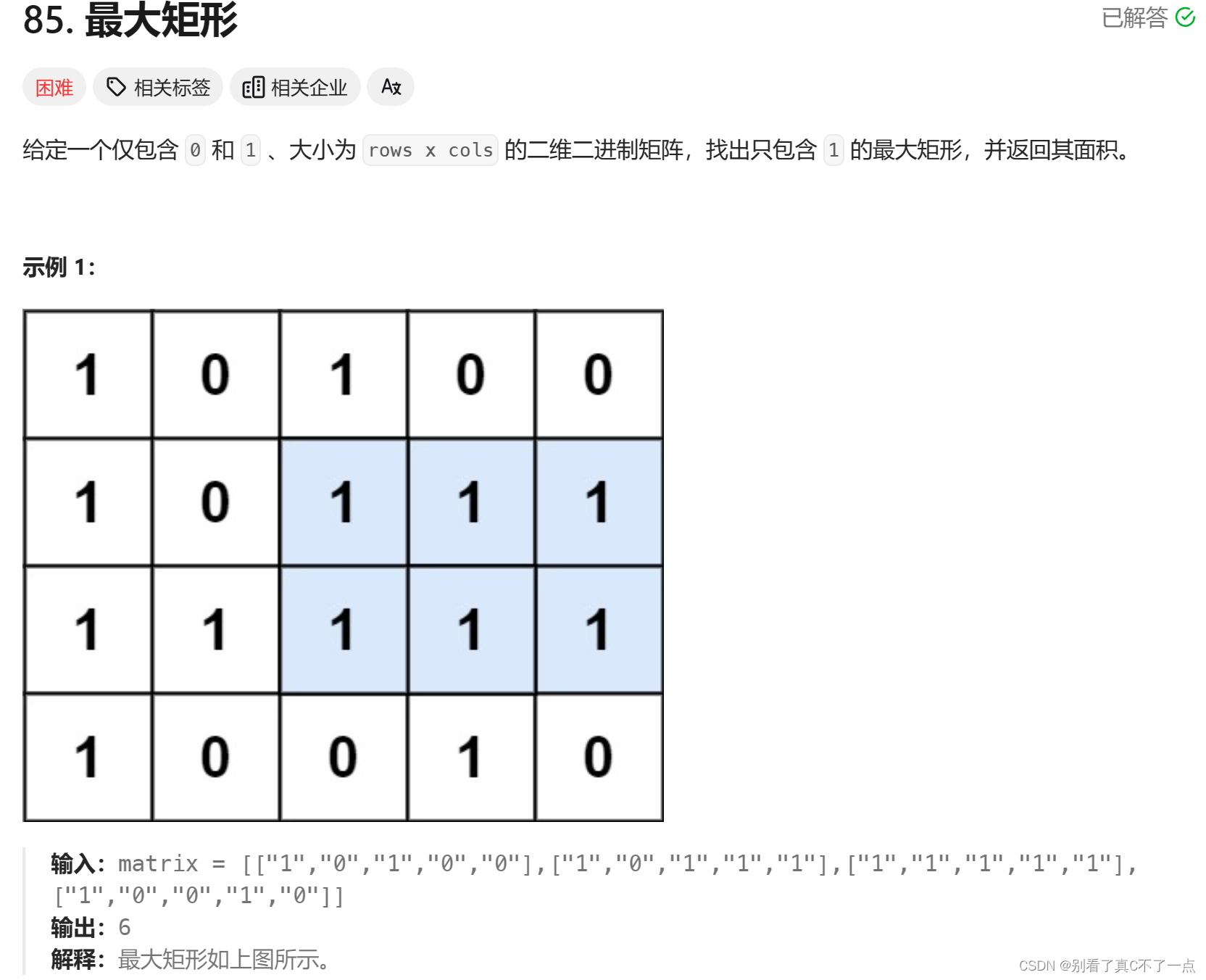
每日5题Day17 - LeetCode 81 - 85
每一步向前都是向自己的梦想更近一步,坚持不懈,勇往直前! 第一题:81. 搜索旋转排序数组 II - 力扣(LeetCode) class Solution {public boolean search(int[] nums, int target) {int n nums.length;if (n…...

后端开发面经系列 --中望C++面经
中望C面经,全部内容! 公众号:阿Q技术站 文章目录 中望C面经,全部内容!一面 8.15 时长45min1、介绍项目相关2、gdb怎么调试的?打断点用什么指令?3、gcc的编译过程4、cmake添加头文件搜索路径用…...
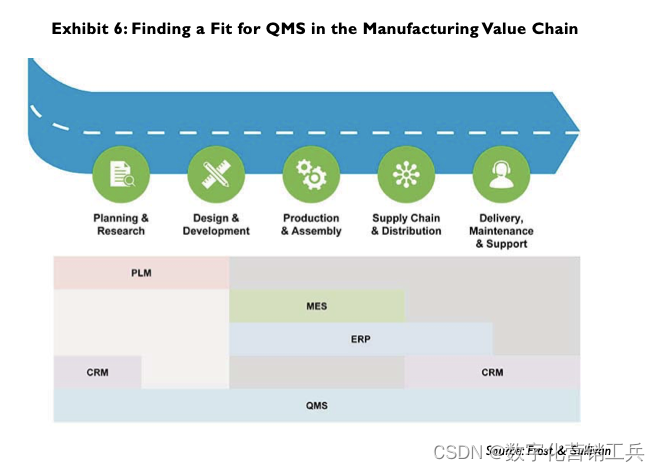
德国西门子论未来质量管理 - 如何与明天相遇?
未来制造业的质量 -- 如何用软件方案满足质量要求 作者:Bill Butcher 翻译&编辑:数字化营销工兵 【前言】在Frost&Sullivan最近发表的一份白皮书中,他们讨论了制造业的质量投资。质量是制造过程的关键要素,但似乎比其他…...
webpack快速入门---webpack的安装和基本使用
webpack是什么 本质上,webpack 是一个用于现代 JavaScript 应用程序的 静态模块打包工具。当 webpack 处理应用程序时,它会在内部从一个或多个入口点构建一个 依赖图(dependency graph),然后将你项目中所需的每一个模块组合成一个或多个 bund…...

后端开发面经系列 -- 华为C++一面面经
HUAWEI – C一面面经 公众号:阿Q技术站 来源:https://www.nowcoder.com/feed/main/detail/b8113ff340d7444985b32a73c207c826 1、计网的协议分几层?分别叫什么? OSI七层模型 物理层 (Physical Layer): 负责物理设备之间的原始比…...
csrf漏洞与ssrf漏洞
环境:用kali搭建的pikachu靶场 一.CSRF 1.CSRF漏洞简介 跨站请求伪造(CSRF)漏洞是一种Web应用程序安全漏洞,攻击者通过伪装成受信任用户的请求来执行未经授权的操作。这可能导致用户在不知情的情况下执行某些敏感操作࿰…...
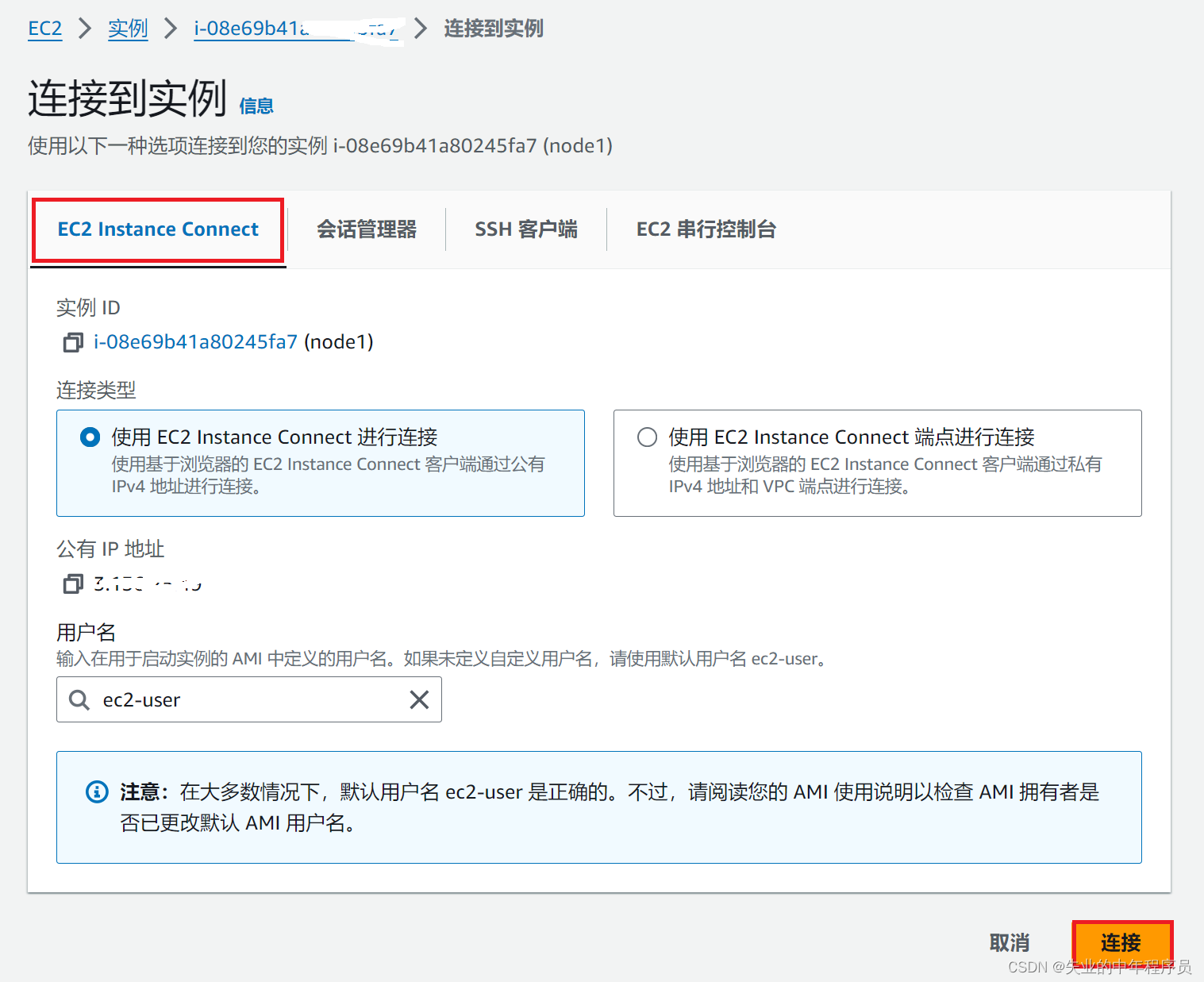
AWS EC2服务器开启root密码,SSH登录
1) EC2 Instance Connect连接,更改root密码 sudo passwd root 2)接着切换到切换到 root 身份,编辑 SSH 配置文件 $ sudo -i$ vi /etc/ssh/sshd_configPasswordAuthentication no,把 no 改成 yes #PermitRootLogin prohibit-passw…...

常见代码版本管理工具
目录 一、引言 二、Gitee (一)优点与特点 (二)缺点 (三)使用报告 三、GitHub 四、SVN 五、总结 一、引言 在软件开发过程中,代码版本控制工具是不可或缺的。Gitee、GitHub和SVN是三种常…...
最新版点微同城源码34.7+全套插件+小程序前后端
带全套插件 自己耐心点配置一下插件 可以H5可以小程序 一款专属的同城服务平台对于企业和个人而言,无疑是拓展业务、提升服务品质的重要一环。点微同城源码搭配全套插件,以及完善的小程序前后端,将为您的业务发展提供强大支持 源码免费下载…...
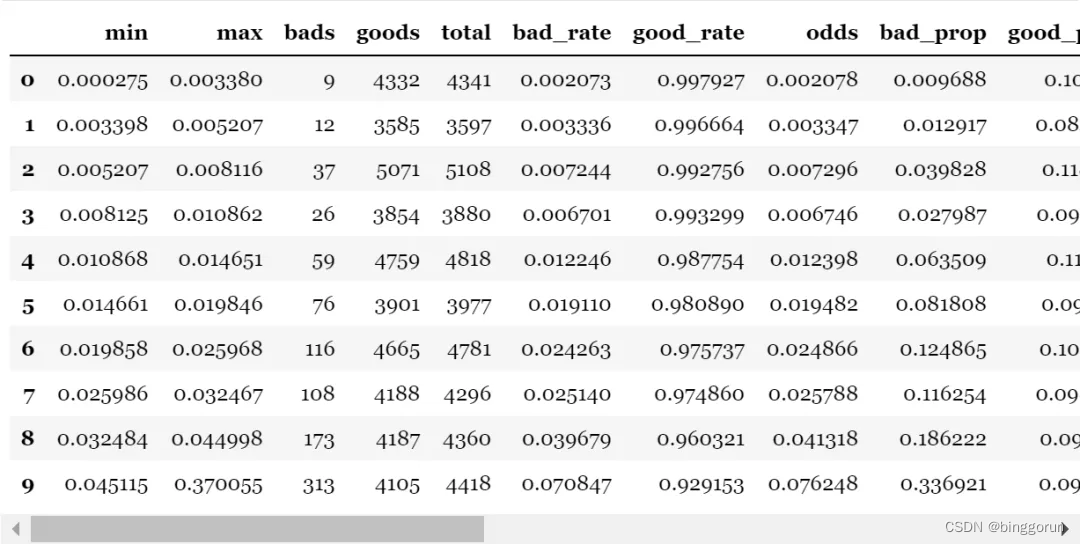
逻辑回归及python实现
概述 logistic回归是一种广义线性回归(generalized linear model),因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同,都具有 w‘xb,其中w和b是待求参数,其区别在于他们的因变量不同&#x…...

大模型押题高考语文作文,带着大模型参加语文高考会怎么样?
前沿 大语言模型通常是指那些经过大量数据训练,能够理解和生成自然语言文本的人工智能系统。这些模型通常具有数百万到数十亿个参数,能够执行多种语言任务,例如语言翻译、文本摘要、问答系统、文本生成等。大语言模型能够捕捉语言的复杂性和细微差别,提供更加准确和自然的…...
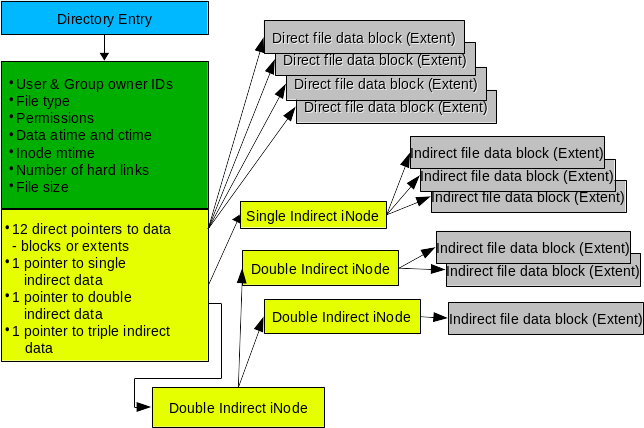
Linux Ext2/3/4文件系统
文章目录 前言一、Linux文件系统简介1.1 简介1.2 Linux File System Structure1.3 Directory Structure 二、Ext2/3/4文件系统2.1 Minix2.2 EXT2.3 EXT22.4 EXT32.5 EXT4 三、EXT Inode参考资料 前言 这篇文章介绍了Linux文件系统的一些基础知识:Linux 文件系统简介…...
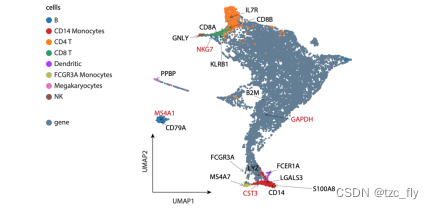
SIMBA方法解读
目录 预处理scRNA-seqscATAC-seq 图构建(5种场景)scRNA-seq分析scATAC-seq分析多模态分析批次整合多模态整合 图学习SIMBA空间中查询实体识别TF-target genes 预处理 scRNA-seq 过滤掉在少于三个细胞中表达的基因。原始计数按文库大小标准化࿰…...

VueRoute url参数
版本 4.x 获取query参数 使用$router.query,可以获取参数对应的json对象。 获取url参数 需要在路由配置中定义。使用$router.param获取。...
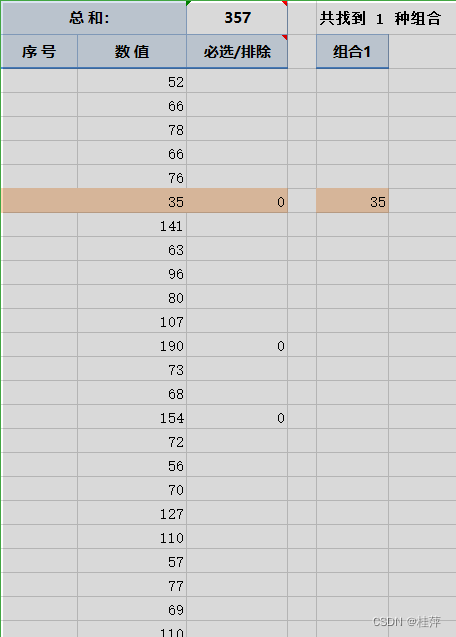
WPS表格插件方方格子【凑数】功能:选出和等于固定数字的数
文章目录 后来发现可以下载方方格子插件,使用【凑数】功能https://ffcell.lanzouj.com/iwhfc1kjhayh【凑数】快速【凑数】 导师让沾发票,需要选出若干个数额的发票,使它们的和等于一个指定数。不知道怎么办了,查了一下,…...

通过SpringCloudGateway中的GlobalFilter实现鉴权过滤
1.pom.xml中加入gateway jar包 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-gateway</artifactId></dependency> 2.创建权限过滤器 SecurityFilter /*** 鉴权过滤***/ Slf4j Component …...

TCP/IP(网络编程)
一、网络每一层的作用 *网络接口层和物理层的作用:屏蔽硬件的差异,通过底层的驱动,会提供统一的接口,供网络层使用 *网络层的作用:实现端到端的传输 *传输层:数据应该交给哪一个任…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
