29、matlab算数运算汇总2:加、减、乘、除、幂、四舍五入
1、乘法:times, .*
语法
C = A.*B 通过将对应的元素相乘来将数组 A 和 B 相乘。
C = times(A,B) 是执行 A.*B 的替代方法,
1)将两个向量相乘
代码及运算
A = [1 0 3];
B = [2 3 7];
C = A.*BC =2 0 21
2) 将两个数组相乘
代码及运算
A = [1 0 3; 5 3 8; 2 4 6];
B = [2 3 7; 9 1 5; 8 8 3];
C = A.*BC =2 0 2145 3 4016 32 182、 mtimes, * 矩阵乘法
语法
语法:C = A*B 是 A 和 B 的矩阵乘积
语法:C = mtimes(A,B) 是执行 A*B 这一操作的替代方法
1)将两个向量相乘
代码及运算
A = [1 1 0 0];
B = [1; 2; 3; 4];
C = A*BC =32) 将两个数组相乘
代码及运算
A = [1 3 5; 2 4 7];
B = [-5 8 11; 3 9 21; 4 0 8];
C = A*BC =24 35 11430 52 1623、prod数组元素的乘积
语法
B = prod(A) 返回 A 的数组元素的乘积。
B = prod(A,"all") 返回 A 的所有元素的乘积
B = prod(A,dim) 返回沿维度 dim 的乘积。
B = prod(___,nanflag) 指定包含还是省略 A 中的 NaN 值。
1)每列中元素的乘积
代码及运算
A=[1:3:7;2:3:8;3:3:9]
B = prod(A)A =1 4 72 5 83 6 9B =6 120 5042) 逻辑输入的乘积
代码及运算
A = [true false; true true]
B = prod(A)A =2×2 logical 数组1 01 1B =1 03) 每行中元素的乘积
代码及运算
A=[1:3:7;2:3:8;3:3:9]
dim = 2;
B = prod(A,dim)A =1 4 72 5 83 6 9B =28801624) 排除缺失值的乘积
代码及运算
A = [1.77 -0.005 NaN -2.95; NaN 0.34 NaN 0.19]
B = prod(A,"omitnan")A =1.7700 -0.0050 NaN -2.9500NaN 0.3400 NaN 0.1900B =1.7700 -0.0017 1.0000 -0.56054、 cumprod 累积乘积
语法
B = cumprod(A) 返回 A 的累积乘积,该累积乘积从 A 中大小大于 1 的第一个数组维度开始计算。
B = cumprod(A,dim) 返回沿维度 dim 计算的元素的累积乘积。
B = cumprod(___,direction) 可在上述任一语法的基础上指定计算方向。
B = cumprod(___,nanflag) 指定包含还是省略 A 中的 NaN 值。
1)向量的累计乘积
说明:说明:计算从 1 到 5 的整数的累积乘积。元素 B(2) 是 A(1) 和 A(2) 的乘积,而 B(5) 是元素 A(1) 至 A(5) 的乘积。
代码及运算
A = 1:5;
B = cumprod(A)B =1 2 6 24 1202) 矩阵列中的累积乘积
代码及运算
A = [1 4 7; 2 5 8; 3 6 9]
B = cumprod(A)A =1 4 72 5 83 6 9B =1 4 72 20 566 120 5043) 矩阵行中的累积乘积
说明:计算 A 的行的累积乘积。元素 B(3) 是 A(1) 和 A(3) 的乘积,而 B(5) 是 A(1)、A(3) 和 A(5) 的乘积。
代码及运算
A = [1 3 5; 2 4 6]
B = cumprod(A,2)A =1 3 52 4 6B =1 3 152 8 484) 不包括缺失值的累积乘积
代码及运算
A = [3 5 NaN 4; 2 6 NaN 9; 1 3 0 NaN]
B = cumprod(A,"omitnan")5、除法rdivide, ./ 数组右除
语法
x = A./B 用 A 的每个元素除以 B 的对应元素。
1)除以两个数值数组
代码及运算
A = [2 4 6 8; 3 5 7 9];
B = 10*ones(2,4);
x = A./Bx =0.2000 0.4000 0.6000 0.80000.3000 0.5000 0.7000 0.90002) 整数除法
代码及运算
a = int16(10);
b = int16([3 4 6]);
x = a./bx =1×3 int16 行向量3 3 23) 数组除以标量
代码及运算
C = 5;
D = magic(3);
x = C./Dx =0.6250 5.0000 0.83331.6667 1.0000 0.71431.2500 0.5556 2.50004) 将行向量和列向量相除
代码及运算
a = 1:2;
b = (1:3)';
a ./ bans =1.0000 2.00000.5000 1.00000.3333 0.66676、 ldivide, .\ 数组左除
语法
x = B.\A 用 A 的每个元素除以 B 的对应元素。
1)除以两个数值数组
代码及运算
A = ones(2,3);
B = [1 2 3; 4 5 6];
x = B.\Ax =1.0000 0.5000 0.33330.2500 0.2000 0.16672) 数值数组除以标量
代码及运算
c = 2;
D = [1 2 3; 4 5 6];
x = D.\cx =2.0000 1.0000 0.66670.5000 0.4000 0.33333) 将行向量和列向量相除
代码及运算
a = 1:2;
b = (1:3)';
b .\ aans =1.0000 2.00000.5000 1.00000.3333 0.66677、power, .^ 按元素求幂
语法
C = A.^B 计算 A 中每个元素在 B 中对应指数的幂。
1)计算向量每个元素的平方
代码及运算
A = 1:5;
C = A.^2C =1 4 9 16 252) 计算每个矩阵元素的倒数
代码及运算
A = [1 2 3; 4 5 6; 7 8 9];
C = A.^-1C =1.0000 0.5000 0.33330.2500 0.2000 0.16670.1429 0.1250 0.11113) 以列向量为指数对行向量按元素求幂
代码及运算
a = [2 3];
b = (1:3)';
a.^bans =2 34 98 274) 计算数的根
代码及运算
A = -1;
B = 1/3;
C = A.^B
C = nthroot(A,3)C =0.5000 + 0.8660iC =-18、mpower, ^ 矩阵幂
语法
C = A^B 计算 A 的 B 次幂并将结果返回给 C。
1)构造方阵
代码及运算
A = [1 2; 3 4];
C = A^2C =7 1015 222)矩阵指数
代码及运算
B = [0 1; 1 0];
C = 2^BC =1.2500 0.75000.7500 1.2500
9、transpose, .' 转置向量或矩阵
语法
B = A.' 返回 A 的非共轭转置,即每个元素的行和列索引都会互换。
1)实矩阵转置
代码及运算
A = magic(4)
B = A.'A =16 2 3 135 11 10 89 7 6 124 14 15 1B =16 5 9 42 11 7 143 10 6 1513 8 12 12) 复矩阵转置
代码及运算
A = [1 3 4-1i 2+2i; 0+1i 1-1i 5 6-1i]
B = A.'A =1.0000 + 0.0000i 3.0000 + 0.0000i 4.0000 - 1.0000i 2.0000 + 2.0000i0.0000 + 1.0000i 1.0000 - 1.0000i 5.0000 + 0.0000i 6.0000 - 1.0000iB =1.0000 + 0.0000i 0.0000 + 1.0000i3.0000 + 0.0000i 1.0000 - 1.0000i4.0000 - 1.0000i 5.0000 + 0.0000i2.0000 + 2.0000i 6.0000 - 1.0000i10、 mod 除后的余数(取模运算)
语法
b = mod(a,m) 返回 a 除以 m 后的余数,其中 a 是被除数,m 是除数
1)标量被除后的余数
代码及运算
b = mod(23,5)b =3
2) 向量被除后的余数
代码及运算
a = 1:5;
m = 3;
b = mod(a,m)b =1 2 0 1 23)正值和负值被除后的余数
代码及运算
a = [-4 -1 7 9];
m = 3;
b = mod(a,m)b =2 2 1 04) 用负除数除后的余数
代码及运算
a = [-4 -1 7 9];
m = -3;
b = mod(a,m)b =-1 -1 -2 05)浮点值被除后的余数
代码及运算
theta = [0.0 3.5 5.9 6.2 9.0 4*pi];
m = 2*pi;
b = mod(theta,m)b =0 3.5000 5.9000 6.2000 2.7168 011、 rem 除后的余数
语法
r = rem(a,b) 返回 a 除以 b 后的余数,其中 a 是被除数,b 是除数。
1)标量被除后的余数
代码及运算
a = 23;
b = 5;
r = rem(a,b)r =32)向量被除后的余数
代码及运算
a = 1:5;
b = 3;
r = rem(a,b)r =1 2 0 1 23) 正值和负值被除后的余数
代码及运算
a = [-4 -1 7 9];
b = 3;
r = rem(a,b)r =-1 -1 1 04) 浮点值被除后的余数
代码及运算
theta = [0.0 3.5 5.9 6.2 9.0 4*pi];
b = 2*pi;
r = rem(theta,b)r =0 3.5000 5.9000 6.2000 2.7168 0
13、idivide 带有舍入选项的整除
语法
C = idivide(A,B) 将 A 的每个元素除以 B 的对应元素,朝零方向舍入到最接近的整数。
C = idivide(A,B,opt) 指定替代舍入选项:'fix'、'floor'、'ceil' 或 'round'。
1)整数除法
代码及运算
A = int16([-7 -4 7 11]);
B = int16(10);
C = idivide(A,B)C =1×4 int16 行向量0 0 0 12)两个整数数组相除
代码及运算
A = int64([-2 3]);
B = int64([3 5]);
C = idivide(A,B)C =1×2 int64 行向量0 03) 整数除法的舍入选项:用默认舍入选项 'fix' 将 A 除以 B 的每个元素。
代码及运算
A = 2.0;
B = int32([-3 3 4]);
C = idivide(A,B)C = idivide(A,B,'floor')
C = idivide(A,B,'ceil')
C = idivide(A,B,'round')C =1×3 int32 行向量0 0 0C =1×3 int32 行向量-1 0 0C =1×3 int32 行向量0 1 1C =1×3 int32 行向量-1 1 1相关文章:

29、matlab算数运算汇总2:加、减、乘、除、幂、四舍五入
1、乘法:times, .* 语法 C A.*B 通过将对应的元素相乘来将数组 A 和 B 相乘。 C times(A,B) 是执行 A.*B 的替代方法, 1)将两个向量相乘 代码及运算 A [1 0 3]; B [2 3 7]; C A.*BC 2 0 212) 将两个数组相乘 代码及运算 A [1 0 3;…...

<Rust><iced>基于rust使用iced库构建GUI实例:动态改变主题色
前言 本专栏是Rust实例应用。 环境配置 平台:windows 软件:vscode 语言:rust 库:iced、iced_aw 概述 本篇构建了这样的一个实例,可以动态修改UI的主题,通过菜单栏来选择预设的自定义主题和官方主题&#…...

k8s——安全机制
一、安全机制说明 Kubernetes作为一个分布式集群的管理工具,保证集群的安全性是其一个重要的任务。API Server是集群内部各个组件通信的中介, 也是外部控制的入口。所以Kubernetes的安全机制基本就是围绕保护API Server来设计的。 比如 kubectl 如果想…...
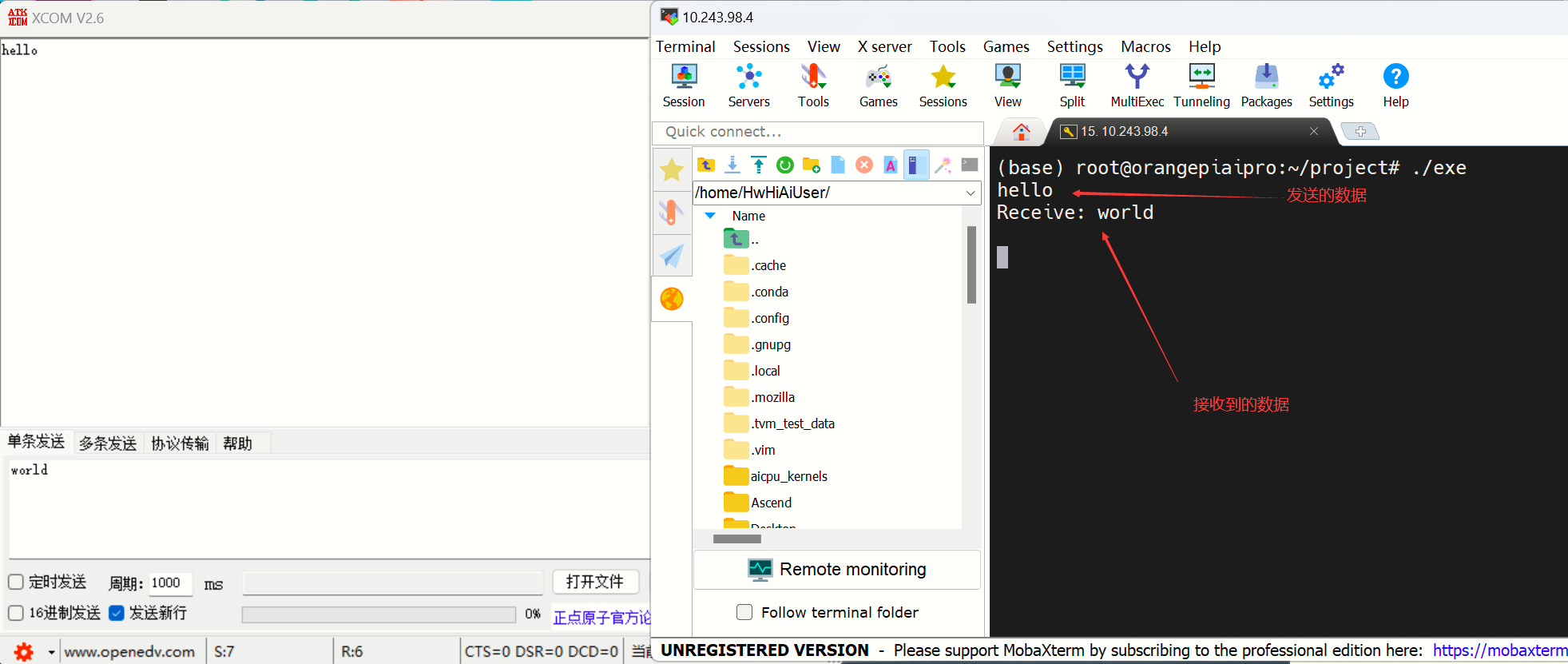
Linux驱动应用编程(三)UART串口
本文目录 前述一、手册查看二、命令行调试串口1. 查看设备节点2. 使用stty命令设置串口3. 查看串口配置信息4. 调试串口 三、代码编写1. 常用API2. 例程线程优化 前述 在开始实验前,请一定要检查测试好所需硬件是否使用正常,不然调试过程中出现的问题&am…...
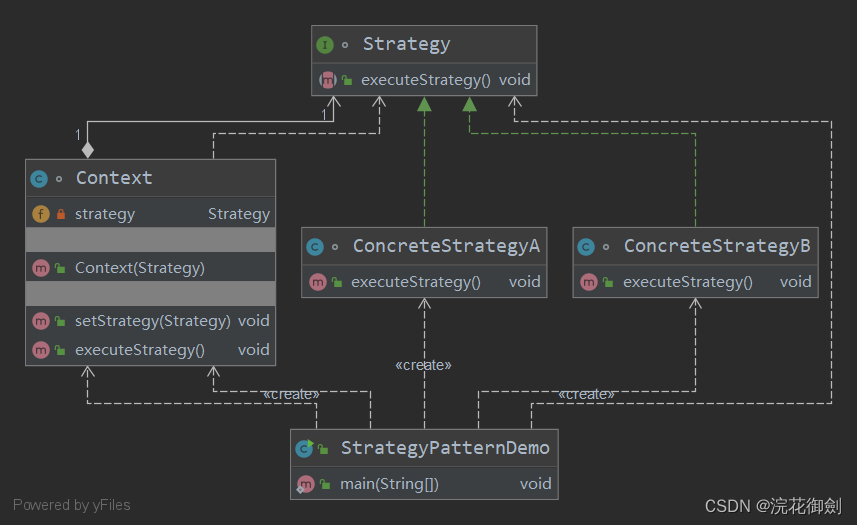
【设计模式深度剖析】【4】【行为型】【策略模式】
文章目录 策略模式定义英文原话直译 角色类图策略接口Strategy:具体策略类上下文类Context测试类 策略模式的应用策略模式的优点策略模式的缺点策略模式的使用场景 策略模式 策略模式(Strategy Pattern) Strategy策略也称作Policy政策。 想…...
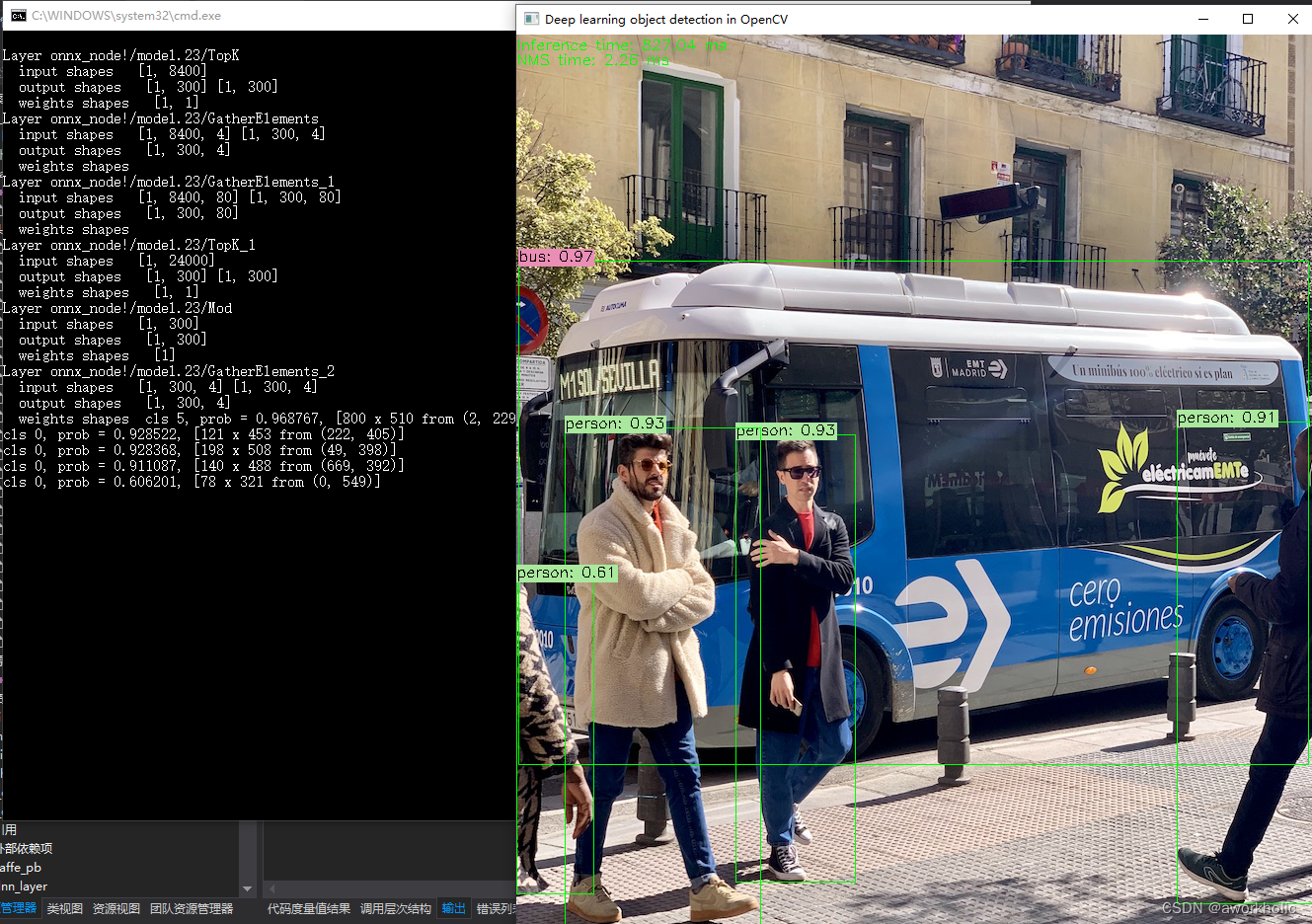
opencv dnn模块 示例(26) 目标检测 object_detection 之 yolov10
文章目录 1、yolov10简要介绍1.1、双标签分配策略1.2、架构改进1.3、性能1.4、预训练模型1.5、网络有关层说明 2、测试2.1、官方测试2.2、opencv dnn2.2.1、仅运行到内部"NMS"步骤之前的层2.2.2、完整代码2.2.2、完整实现所有层 2.3、onnxruntime测试2.4、tensorrt 1…...
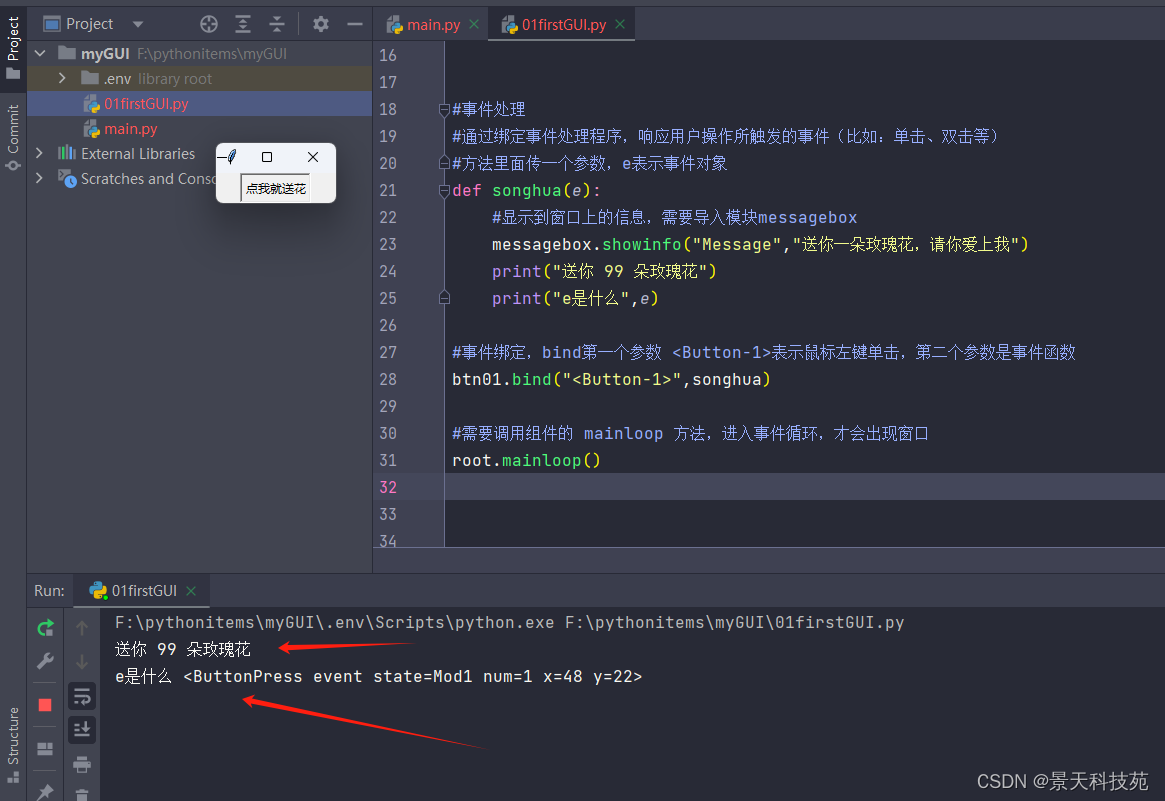
【python进阶】python图形化编程之美--tkinter模块初探
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...
discuz点微同城源码34.7+全套插件+小程序前端
discuz点微同城源码34.7全套插件小程序前后端 模板挺好看的 带全套插件 自己耐心点配置一下插件 可以H5可以小程序...
ActiveMQ 介绍、下载、安装和控制台
ActiveMQ 介绍 Apache ActiveMQ 是一款非常成熟且功能全面的开源消息中间件,由Apache软件基金会维护。它遵循 Java Message Service (JMS) 规范,这意味着它提供了一组标准的 API,允许 Java 应用程序以一种标准化的方式发送和接收消息。 以下…...
MacOS M系列芯片一键配置多个不同版本的JDK
第一步:下载JDK。 官网下载地址:Java Archive | Oracle 选择自己想要下载的版本,一般来说下载一个jdk8和一个jdk11就够用了。 M系列芯片选择这两个,第一个是压缩包,第二个是dmg可以安装的。 第二步:编辑…...
源码文章上传无忧,论坛小程序支持
前言 在数字化时代,知识的分享与传播显得愈发重要。为了满足广大创作者和求知者的需求,我们推出了全新的论坛小程序,不仅支持文章、源码、链接等多样化内容的上传,还实现了付费观看功能,为创作者们提供了一个展示才华…...

Docker面试整理-如何优化Docker容器的性能?
优化Docker容器的性能可以从多个方面入手,以下是一些建议: 选择合适的基础镜像:使用轻量级的基础镜像,如基于Alpine Linux的镜像,可以减少镜像的大小和启动时间。避免使用过于庞大的操作系统镜像。优化Dockerfile:减少Dockerfile中的不必要指令和层,以最小化镜像的大小。…...
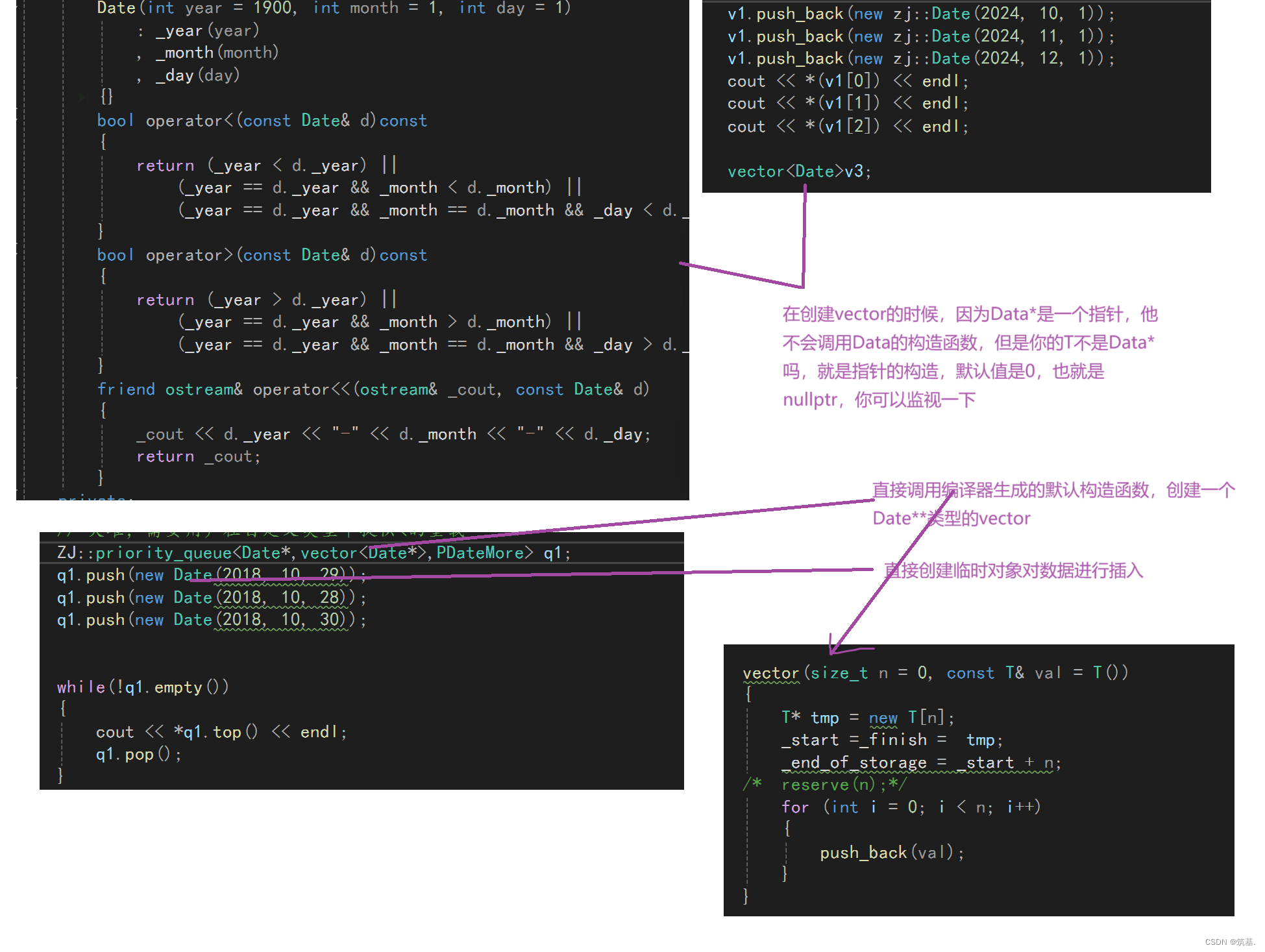
list(二)和_stack_queue
嗨喽大家好,时隔许久阿鑫又给大家带来了新的博客,list的模拟实现(二)以及_stack_queue,下面让我们开始今天的学习吧! list(二)和_stack_queue 1.list的构造函数 2.设计模式之适配器和迭代器 3.新容器de…...
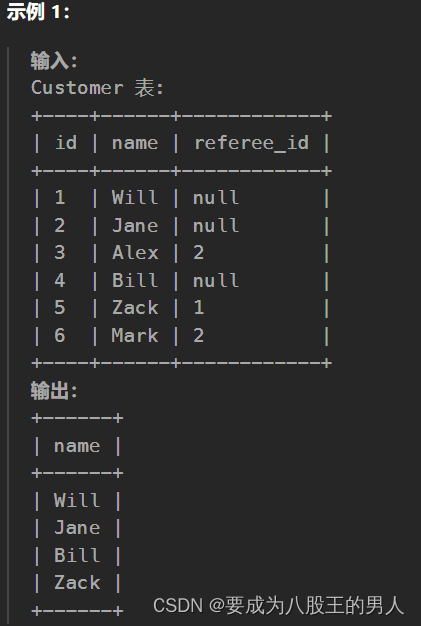
查询SQL02:寻找用户推荐人
问题描述 找出那些 没有被 id 2 的客户 推荐 的客户的姓名。 以 任意顺序 返回结果表。 结果格式如下所示。 题目分析: 这题主要是要看这null值会不会用,如果说Java玩多了,你去写SQL时就会有问题。在SQL中判断是不是null值用的是is null或…...
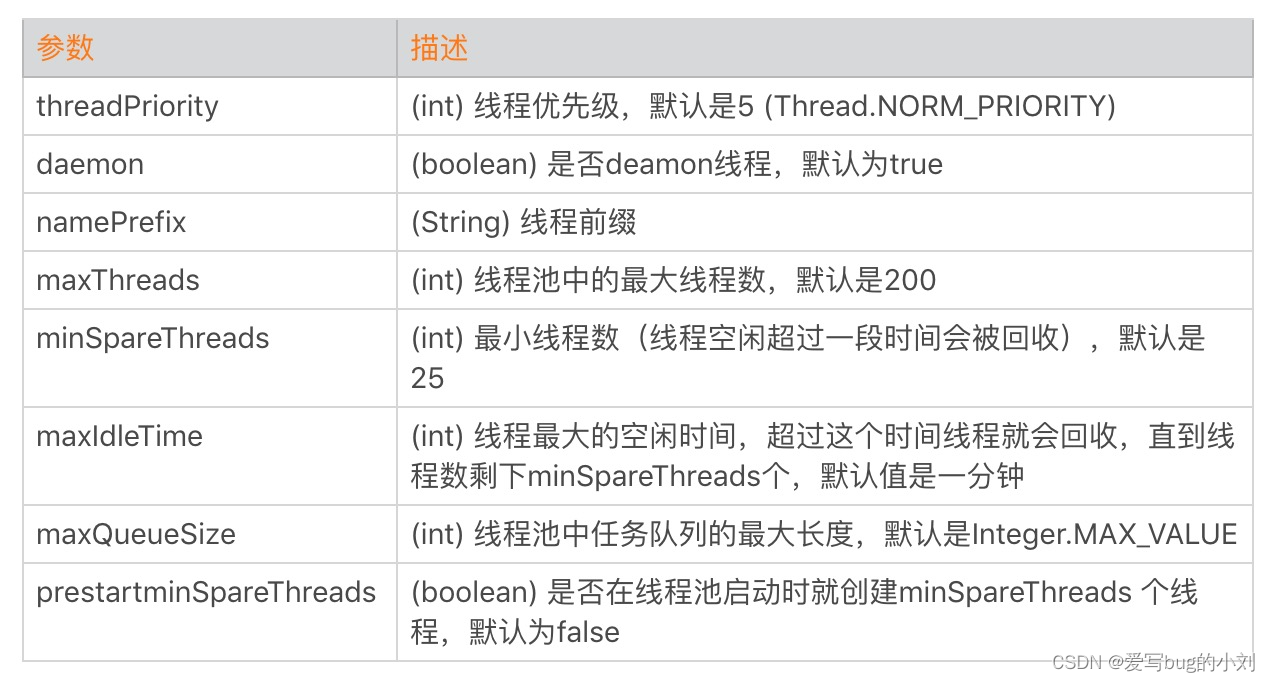
2、Tomcat 线程模型详解
2、Tomcat 线程模型详解 Tomcat I/O模型详解Linux I/O模型详解I/O要解决什么问题Linux的I/O模型分类 Tomcat支持的 I/O 模型Tomcat I/O 模型如何选型 网络编程模型Reactor线程模型单 Reactor 单线程单 Reactor 多线程主从 Reactor 多线程 Tomcat NIO实现Tomcat 异步IO实现 Tomc…...

对硬盘的设想:纸存、执行存
固态硬盘出现后,发现它的擦写次数受限,越是便宜的固态硬盘,擦写次数越少。于是,有了“纸存”的设想,即硬盘上的单元只能改写一次,就像拿钢笔在纸上写字一样。这时,文件系统、数据库该怎么设计&a…...
最新付会进群多群同时变现社群系统V3.5.3版本 详细教程+源码下载
市面1888最新付费进群多群同时变现系统V3.5.3版本 详细教程源码下载介绍: 续男粉变现,相亲群变现后 演化出来的最新多群同时变现系统 可同时进行40个群同时变现 可设置地域群,相亲,男粉变现等多种群 购买后包括详细的 域名服…...
python tk实现标签切换页面
import tkinter as tk from tkinter import ttk# 初始化主窗口 root tk.Tk() root.title("标签页示例")# 设置窗口大小 root.geometry("400x300")# 创建 Notebook 小部件 notebook ttk.Notebook(root) notebook.pack(expandTrue, fill"both")#…...
引擎:UI
一、控件介绍 Button 按钮 创建一个按钮 按钮禁用 精灵模式 颜色模式 缩放模式 绑定点击事件 EditBox 输入框 Layout 布局 支持水平排列、垂直排列、背包排列 PageView 页面视图 ProgressBar 进度条 RichText 富文本 绑定点击事件 事件可以被其它标签包裹 图文混排 Scroll…...

Redis常见异常及优化方案
Redis常见异常及优化方案 Redis集群(redis-cluster)中的三主三从或者哨兵(sentinel)模式配置是一种常见的高可用架构,用于解决单点故障和提高数据可靠性。然而,即使在这样的配置下,仍然可能会遇…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...
