超长正整数的加法
一、引言
在计算机科学中,整数加法是一个基础且重要的操作。然而,当面对超长正整数(即超出计算机内置整数类型表示范围的整数)时,传统的整数加法方法便不再适用。超长正整数通常使用字符串或数组来表示,每一位对应整数的一个数字。因此,实现超长正整数的加法就需要一些特殊的技巧和算法。本文将详细探讨如何实现超长正整数的加法,并提供C++代码示例。
二、算法设计
超长正整数的加法算法可以借鉴手工进行大数加法的思路。具体步骤如下:
- 从最低位(即字符串的末尾或数组的尾部)开始,逐位相加。
- 将每一位的加法结果(0-18)分为两部分:进位(0或1)和当前位的值(0-9)。
- 将进位加到下一位的加法结果中,并重复步骤2,直到所有位都处理完毕。
- 如果最高位仍有进位,需要在结果前添加一个数字“1”。
- 转换回字符串或数组形式,得到最终的加法结果。
三、C++代码实现
下面是一个使用C++实现的超长正整数加法的示例代码:
#include <iostream>
#include <string>
#include <algorithm>// 辅助函数:将两个数字相加并返回结果和进位
std::pair<int, int> addDigits(int a, int b, int &carry) {int sum = a + b + carry;carry = sum / 10;return {sum % 10, carry};
}// 超长正整数加法函数
std::string addBigNumbers(const std::string &num1, const std::string &num2) {// 反转字符串以便从最低位开始相加std::string reversedNum1 = num1;std::string reversedNum2 = num2;std::reverse(reversedNum1.begin(), reversedNum1.end());std::reverse(reversedNum2.begin(), reversedNum2.end());// 确保num1是较长的数if (reversedNum2.size() > reversedNum1.size()) {std::swap(reversedNum1, reversedNum2);}// 初始化结果字符串和进位std::string result;int carry = 0;// 逐位相加for (size_t i = 0; i < reversedNum1.size(); ++i) {int digit1 = reversedNum1[i] - '0';int digit2 = (i < reversedNum2.size()) ? (reversedNum2[i] - '0') : 0;auto [sumDigit, newCarry] = addDigits(digit1, digit2, carry);result.push_back(sumDigit + '0');carry = newCarry;}// 处理最高位的进位if (carry > 0) {result.push_back(carry + '0');}// 反转结果字符串并返回std::reverse(result.begin(), result.end());return result;
}// 主函数
int main() {std::string num1, num2;std::cout << "请输入第一个超长正整数:";std::cin >> num1;std::cout << "请输入第二个超长正整数:";std::cin >> num2;std::string sum = addBigNumbers(num1, num2);std::cout << "两数之和为:" << sum << std::endl;return 0;
}
四、代码解释
addDigits函数:这是一个辅助函数,用于将两个数字和一个进位相加,并返回结果和新的进位。addBigNumbers函数:这是实现超长正整数加法的核心函数。首先,它反转输入的两个字符串,以便从最低位开始相加。然后,它遍历较短的字符串(或两个字符串中的每一位),逐位相加,并使用addDigits函数处理进位。最后,它处理最高位的进位(如果有的话),并反转结果字符串以得到正确的顺序。main函数:这是程序的主入口。它首先接收用户输入的两个超长正整数,然后调用addBigNumbers函数计算它们的和,并输出结果。
五、性能优化与边界情况处理
在实现超长正整数的加法时,除了基本的算法设计外,我们还需要考虑一些性能优化和边界情况的处理。
1. 性能优化
- 预分配内存:在构建结果字符串时,我们可以预先估计结果字符串的长度,并一次性分配足够的内存空间。这样可以避免在添加新字符时频繁地重新分配内存,从而提高性能。
- 避免不必要的字符串反转:在上面的示例代码中,我们对输入字符串进行了两次反转操作(一次是为了从最低位开始相加,另一次是为了得到正确的结果顺序)。我们可以优化这个步骤,只进行一次反转操作,即在生成结果字符串时直接按照正确的顺序添加字符。
2. 边界情况处理
- 空字符串或零值:当输入字符串为空或表示零值时,我们需要特殊处理。例如,如果两个输入字符串都是空字符串或表示零值,则结果也应该是一个空字符串或表示零值。
- 前导零:在生成结果字符串时,我们可能需要删除前导零。虽然前导零在数学上不影响整数的值,但在某些应用中可能需要将它们删除以获得更简洁的表示。
3. 错误处理
- 非法输入:我们应该确保输入字符串只包含有效的数字字符。如果输入包含非数字字符,我们应该能够检测并处理这种错误情况。
- 溢出处理:虽然超长正整数的加法本身不会导致溢出(因为我们可以使用任意长度的字符串或数组来表示结果),但在某些情况下,我们可能需要处理与超长正整数加法相关的溢出问题。例如,当我们试图将结果存储在一个固定长度的变量中时,可能会发生溢出。在这种情况下,我们应该能够检测并处理这种错误情况。
4. 示例代码优化
下面是一个优化后的示例代码,它包含了上述提到的一些改进:
#include <iostream>
#include <string>
#include <stdexcept>// 辅助函数:将两个数字相加并返回结果和进位
std::pair<int, int> addDigits(int a, int b, int &carry) {int sum = a + b + carry;carry = sum / 10;return {sum % 10, carry};
}// 超长正整数加法函数(优化版)
std::string addBigNumbers(const std::string &num1, const std::string &num2) {if (num1.empty() && num2.empty()) {return "0"; // 如果两个数都是空字符串,则返回"0"}// 确保num1是较长的数std::string maxNum = num1;std::string minNum = num2;if (num2.size() > num1.size()) {std::swap(maxNum, minNum);}int carry = 0;std::string result;int i = maxNum.size() - 1, j = minNum.size() - 1;// 逐位相加while (i >= 0) {int digit1 = i >= 0 ? maxNum[i] - '0' : 0; // 处理maxNum的剩余位数int digit2 = j >= 0 ? minNum[j] - '0' : 0; // 处理minNum的剩余位数auto [sumDigit, newCarry] = addDigits(digit1, digit2, carry);result.push_back(sumDigit + '0');carry = newCarry;--i;--j;}// 处理最高位的进位if (carry > 0) {result.push_back(carry + '0');}// 去除前导零(如果有的话)while (!result.empty() && result.front() == '0') {result.erase(0, 1);}return result;
}// 主函数(略)
// ...
在这个优化后的示例代码中,我们添加了对空字符串和零值的特殊处理,并在逐位相加时直接处理了两个输入字符串的剩余位数。此外,我们还添加了一个去除前导零的步骤,以确保结果字符串的简洁性。
相关文章:

超长正整数的加法
一、引言 在计算机科学中,整数加法是一个基础且重要的操作。然而,当面对超长正整数(即超出计算机内置整数类型表示范围的整数)时,传统的整数加法方法便不再适用。超长正整数通常使用字符串或数组来表示,每…...
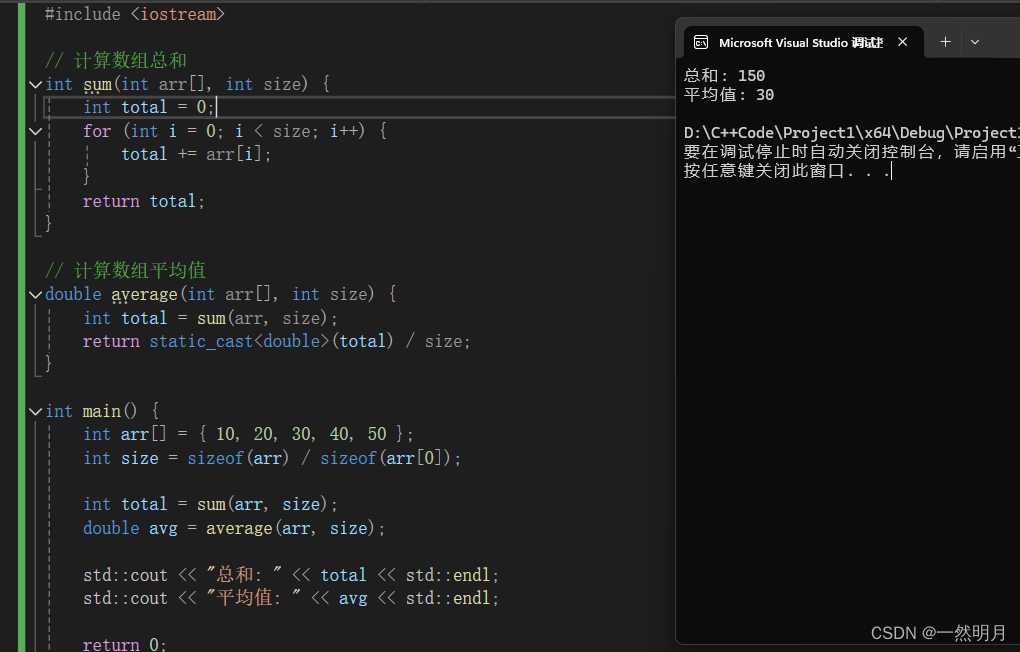
C++ - 查找算法 和 其他 算法
目录 一. 查找算法: 1.顺序查找: 2.二分查找: 二. 其他算法: 1.遍历算法: 2.求和、求平均值等聚合算法。 a.求和算法: b.求平均值算法: 一. 查找算法: 1.顺序查找࿱…...
和槽(SLOT)的宏连接方式弊端)
字符串的信号(SIGNAL)和槽(SLOT)的宏连接方式弊端
字符串的信号(SIGNAL)和槽(SLOT)的宏连接方式在 Qt 4 及早期版本中广泛使用,但这种方法确实存在一些缺点,主要包括以下几点: 类型安全性缺失:由于 SIGNAL 和 SLOT 宏接受的是字符串参…...

Kali linux学习入门
Kali linux学习入门 文章目录 Kali linux学习入门Kali Linux简介Kali Linux工具篇Kali Docker安装Docker 更换国内镜像源Kali 安装 docker compose Kali Linux文档篇Kali Linux 社区篇 Kali Linux简介 Kali Linux是专门用于渗透测试linux操作系统,它由BackTrack发展…...

selenium中,怎么判断是否已选多选框
html文件 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title> </head> <body><p>测试勾选</p><div><input type"checkbox" name"b…...
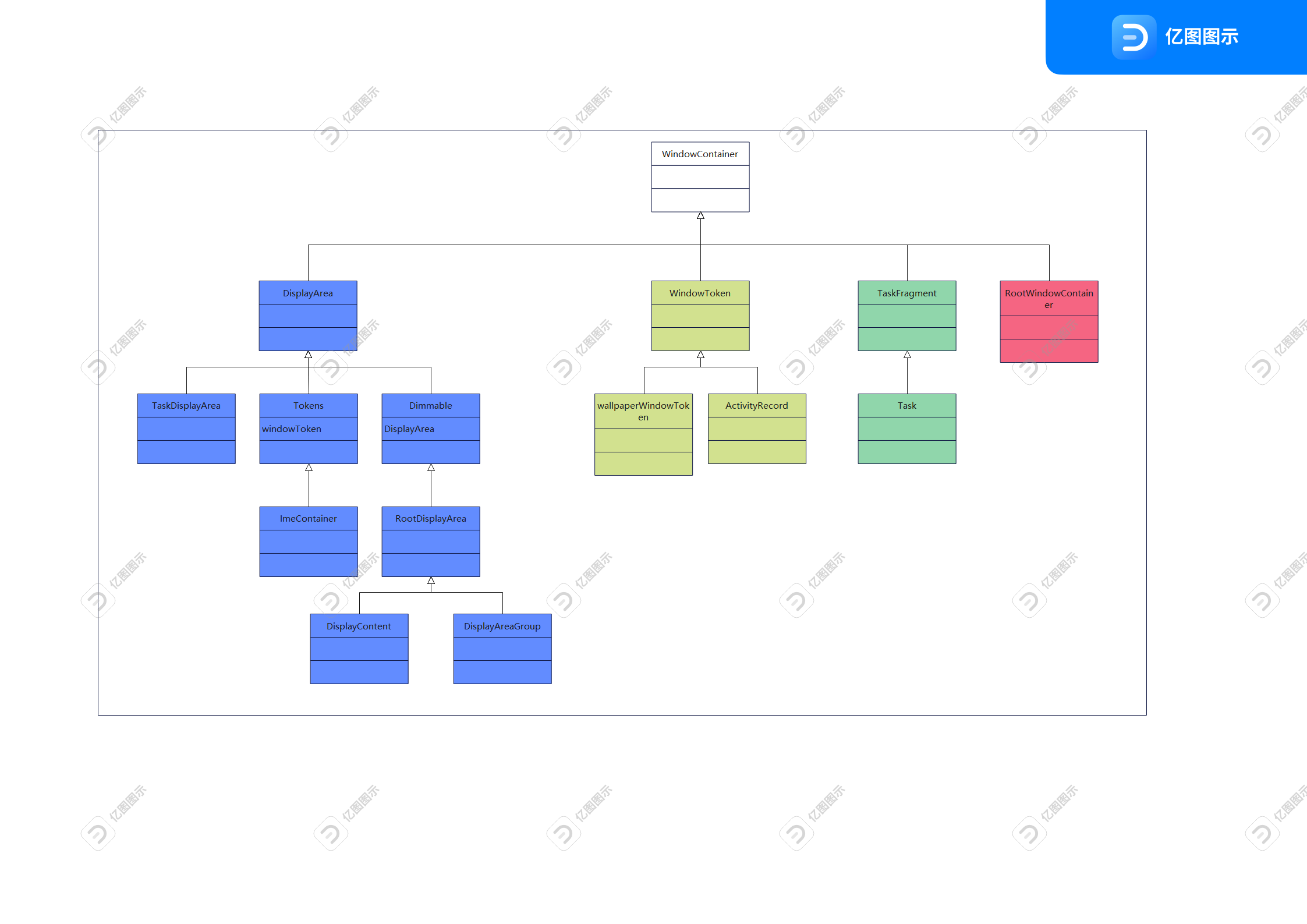
WindowManager相关容器类
窗口中容器类介绍: 本节内容较多,建议结合前面的内容一起阅读: 1、addWindow的宏观概念 2、WindowManager#addView_1 3、WindowManager#addView_2 1)、WindowContainer: class WindowContainer<E extends WindowC…...
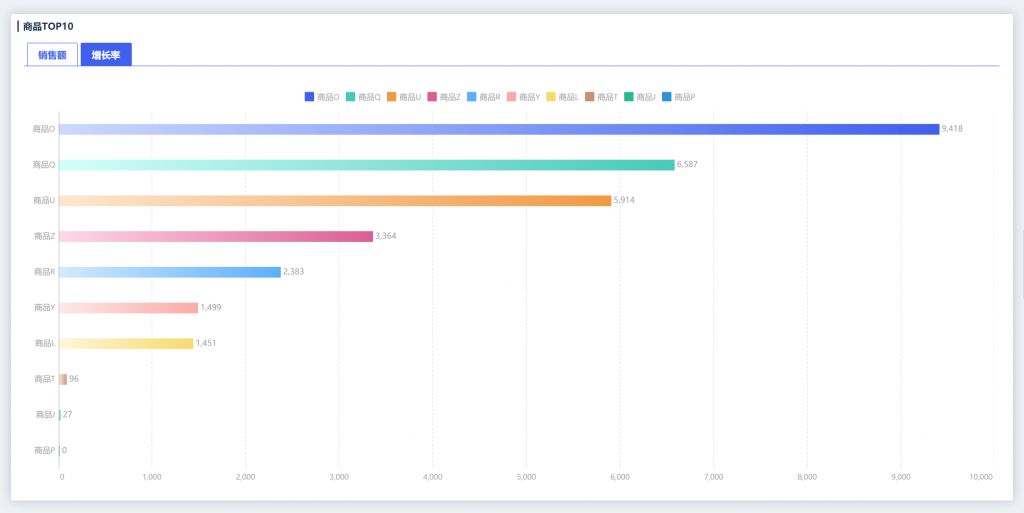
零售行业运营有哪些业务场景?详解各业务场景的分析指标和维度
在当今这个数字化迅速发展的时代,零售行业正经历着前所未有的变革。传统的零售模式正在被新兴的技术和创新的业务场景所颠覆,消费者的需求和购物习惯也在不断地演变。零售行业的运营,作为连接消费者、产品和市场的关键环节,对于零…...

无锡哲讯携手SAP,赋能装备制造业数字化转型
在当今快速发展的工业4.0时代,装备制造业作为国民经济的重要支柱,正面临着前所未有的机遇与挑战。无锡哲讯智能科技有限公司凭借其深厚的行业经验和专业的SAP实施能力,为装备制造业提供全面的数字化解决方案,助力企业实现智能化、…...
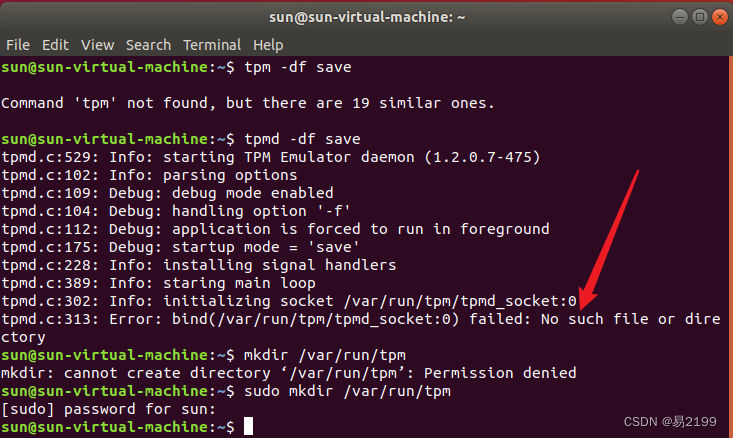
TPM仿真环境搭建
文章目录 背景及注意事项一、CMake二、m4三、GNU MP Library四、TPM_Emulator五、TSS协议栈(trousers-0.3.14.tar.gz)六、 tpm-tools七、查看是否安装成功八、测试 TPM环境(需要开三个终端分别运行)8.1 启动TPM (第一个…...
:使用Processing创作互动艺术:从灵感到实现)
提高篇(五):使用Processing创作互动艺术:从灵感到实现
提高篇(五):使用Processing创作互动艺术:从灵感到实现 引言 互动艺术将观众从被动的观察者转变为主动参与者,通过创意编程和技术手段,让艺术品具备感知和回应的能力。Processing作为一种强大的创意编程工具,提供了丰富的功能和灵活的编程环境,帮助艺术家和设计师实现他…...

华为od-C卷100分题目-3用连续自然数之和来表达整数
华为od-C卷100分题目-3用连续自然数之和来表达整数 题目描述 一个整数可以由连续的自然数之和来表示给定一个整数,计算该整数有几种连续自然数之和的表达式,且打印出每种表达式 输入描述 一个目标整数T(1<T<1000) 输出描述 该整数的所有表达…...

Chrome 自动执行 JS 脚本 | Tampermonkey 插件
文章目录 第 1 步:安装插件 Tampermonkey第 2 步:固定到工具栏第 3 步:在网站上启用 Tampermonkey第 4 步:查看效果第 5 步:调试 JS 代码😂 背景:有个网站,每次进去都要点 3 次才能把相关页面展开。而且,页面经常会自己刷新,导致展开的页面又收回去了。【这一天天的…...

ffmplay 源码解读
stream_open 讲解 // 定义一个静态函数用于初始化并返回VideoState结构体指针,用于管理播放状态 static VideoState* stream_open(const char* filename, AVInputFormat* iformat) {VideoState* is; // 创建VideoState结构体指针// 分配内存并初始化VideoState结构…...

java web如何调用py脚本文件
Controller public class IndexController {RequestMapping("/pythonTest")ResponseBodypublic String pythonTest(){// 假设你的Python脚本名为script.pyString pythonScriptPath "D:\\project\\c1\\hello.py";ProcessBuilder processBuilder new Proce…...

K8s:无状态
无状态服务 无状态服务是指服务的实例之间没有持久化状态,每个实例都是相同的,可以互换使用。 调度器 ReplicationController 简称 RC是 Kubernetes 早期版本中用来确保 Pod 副本始终运行的 API 对象。它通过监控 Pod 副本的数量,确保任何…...
-- 使用 Maven 插件 构建 Docker 镜像)
Docker 入门篇(九)-- 使用 Maven 插件 构建 Docker 镜像
在这篇教程中,我们将学习如何使用 Maven 插件为 Spring Boot 应用构建 Docker 镜像。我们将使用 spring-boot-maven-plugin 和 dockerfile-maven-plugin 这两个插件。 一、前提条件 已安装 Docker。已安装 JDK 8 或以上版本。已安装 Maven。 二 创建一个 Spring …...
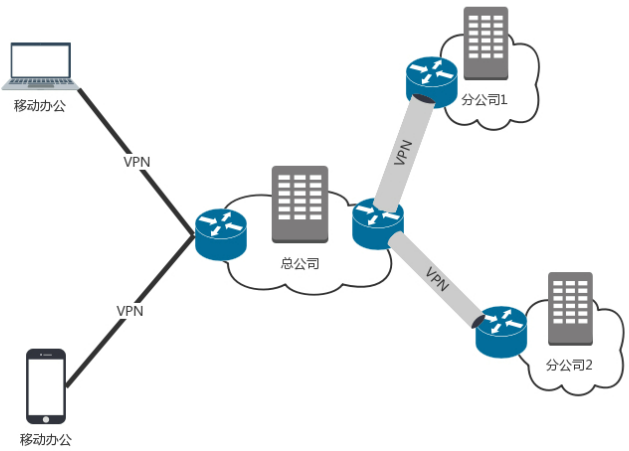
网络协议三
数据中心 一、DNS 现在网站的数目非常多,常用的网站就有二三十个,如果全部用 IP 地址进行访问,恐怕很难记住 根 DNS 服务器 :返回顶级域 DNS 服务器的 IP 地址 顶级域 DNS 服务器:返回权威 DNS 服务器的 IP 地址 …...

LeetCode LRU缓存
题目描述 请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。 实现 LRUCache 类: LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,…...

Parallels Desktop for Mac 19.4.0更新了哪些内容?有什么改进?
带来了重新设计的共享 Mac 文件夹版本,这些文件夹现在是符号链接,像指针一样指向您的 Mac 文件夹中的文件,同时仍然显示在 Windows 的本地磁盘上。 修复了由于共享文件夹问题导致 NinjaTrader 无法正常启动的问题。 修复了由于共享文件夹问…...
Python 将CSV文件转为PDF文件
CSV文件通常用于存储大量的数据,而PDF文件则是一种通用的文档格式,便于与他人共享和打印。将CSV文件转换成PDF文件可以帮助我们更好地管理和展示数据。本文将介绍如何通过Python编程将CSV文件导出为PDF文件。 Python Excel库安装及介绍 在 Python 中&am…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
