【代码训练营】day54 | 392.判断子序列 115.不同的子序列
所用代码 java
判断子序列 LeetCode 392
题目链接:判断子序列 LeetCode 392 - 简单
思路
这题和之前求最长公共子序列一样。
-
dp[i] [j]:以i-1为结尾的字符串s 和 以j-1为结尾的字符串t 组成的相同子序列的长度
-
递推公式:
- 相等
dp[i][j] = dp[i-1][j-1] - 不相等
dp[i][j] = dp[i][j-1]
- 相等
-
初始化:0行0列无意义,初始化为0
-
遍历顺序
-
打印dp
class Solution {public boolean isSubsequence(String s, String t) {int n1 = s.length();int n2 = t.length();int[][] dp = new int[n1+1][n2+1];for (int i = 1; i <= n1; i++) {for (int j = 1; j <= n2; j++) {if (s.charAt(i-1) == t.charAt(j-1)){dp[i][j] = dp[i-1][j-1] + 1;}else {dp[i][j] = dp[i][j-1];}}
// System.out.println(Arrays.toString(dp[i]));}return dp[n1][n2] == n1;}
}
总结
本题和昨天的最长公共子序列几乎一模一样,甚至更简单一点。因为我们只用判断字符串s是不是子序列就行了,而不用去两个字符串里面找相同的子序列。
不同的子序列 LeetCode 115
题目链接:不同的子序列 LeetCode 115 - 困难
思路
无。
s里面如何删除元素可以得到t?
-
dp[i] [j]:以i-1为结尾的s中有以j-1为结尾的t的个数为dp[i] [j]
-
递推公式:
-
相等
if(s[i-1] == t[j-1])- 使用i-1:
dp[i][j] = dp[i-1][j-1] - 不使用i-1:
dp[i-1][j] - 不用考虑是否使用t,因为t是子串
- 使用i-1:
-
不等
else dp[i][j] = dp[i-1][j]
-
-
初始化:
- 第一行(子串空字符串,所以主串只有全部删完的情况)
dp[i][0] = 1 - 第一列(主串s为空串,所以没有能匹配的情况)
dp[0][j] = 0 dp[0][0] = 1
- 第一行(子串空字符串,所以主串只有全部删完的情况)
-
打印dp
class Solution {public int numDistinct(String s, String t) {int n1 = s.length();int n2 = t.length();int[][] dp = new int[n1+1][n2+1];// 初始化// n1=0, 即空串中包含子序列t的情况为0// n2=0, 即s中包含子序列为空串的情况为1// n1=0,n2=2, 即空串中包含空串的情况为1for (int i = 0; i < n1; i++) {dp[i][0] = 1;}
for (int i = 1; i <= n1; i++) {for (int j = 1; j <= n2; j++) {if (s.charAt(i-1) == t.charAt(j-1)){// 相等的情况,由双方的上一位,加上s的上一位决定(删掉s对应的数)dp[i][j] = dp[i-1][j-1] + dp[i-1][j];}else {// 不相等的情况,由s的上一位觉得(删掉s对应的数)dp[i][j] = dp[i-1][j];}}}return dp[n1][n2];}
}
总结
我们可以打印出来dp数组以便更好的理解该题,上侧还有一种i=0的情况全为0(0,0为1)
Finished:Your input:"babgbag""bag"Output:5Expected:5stdout:1 0 0 0[1, 1, 0, 0][1, 1, 1, 0][1, 2, 1, 0][1, 2, 1, 1][1, 3, 1, 1][1, 3, 4, 1][0, 3, 4, 5]
可以看到s的第一个字母b和t的第一个字母b一样,所以匹配成功,即dp[1][1] = 1,
然后s的第一个字母b和t的第二个字母a不匹配,所以应看s的前一个字母(上一行),即dp[1][2] = 0
最后s的第一个字母b和t的第三个字母g不匹配,所以dp[1][2] = 0
…
我们看s取第二个b的时候,也就是第三行数据,由于t的第一个字母也是b,匹配成功,即dp[3][1]等于双方各删一个值的情况(t删了为空串,匹配,结果为1)加 仅s删一个值的情况(回退一位到s取a,此时s为ba.gbgab,也前面也有传递的结果1),所以dp[3][2]= 2
…
…
我们每次都这样往后推,相等即都删掉一个数,不等即为s删掉一个数,把前面的结果往后利用,就可以得到包含所有子串的数量。
相关文章:

【代码训练营】day54 | 392.判断子序列 115.不同的子序列
所用代码 java 判断子序列 LeetCode 392 题目链接:判断子序列 LeetCode 392 - 简单 思路 这题和之前求最长公共子序列一样。 dp[i] [j]:以i-1为结尾的字符串s 和 以j-1为结尾的字符串t 组成的相同子序列的长度 递推公式: 相等dp[i][j] d…...
【unity3D】创建TextMeshPro(TMP)中文字体(解决输入中文乱码问题)
💗 未来的游戏开发程序媛,现在的努力学习菜鸡 💦本专栏是我关于游戏开发的学习笔记 🈶本篇是unity的TMP中文输入显示乱码的解决方式 创建 TextMeshPro 中文字体遇到的问题描述解决方式Font Asset Creator 面板扩展中文字体文本遇到…...

JAVA开发(JAVA中的异常)
在java开发与代码运行过程中,我们经常会遇到需要处理异常的时候。有时候是在用编辑器写代码,点击保存的时候,编辑器就提示我们某块代码有异常,强制需要处理。有时候是我们启动,运行JAVA代码的时候的,日志里…...
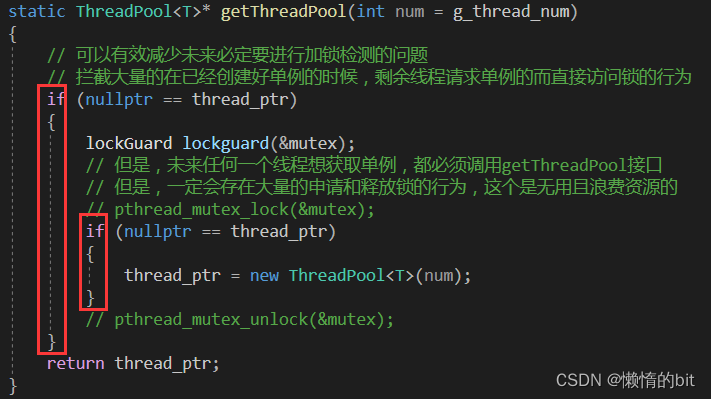
lesson8-Linux多线程
Linux线程概念 线程在进程内部执行,是OS调度的基本单位OS是可以做到让进程进行资源的细粒度划分的物理内存是以4kb为单位的我们的.exe可执行程序本来就是按照地址空间的方式进行编译的页表映射 - 详细图 理解线程 线程在进程的地址空间内运行, 进程内部具有多个执行流的,而线程…...

python的django框架从入门到熟练【保姆式教学】第四篇
在前三篇博客中,我们介绍了Django的模型层、数据库迁移、视图层和URL路由。本篇博客将介绍Django的模板层,讲解如何使用模板来创建美观的Web页面。 模板层(Template) Django的模板层是Django应用程序的另一个核心组件。模板是一…...
)
Codeforces Round 852 (Div. 2)
A Yet Another Promotion 题意:要买n千克物品,第一天的价格为a,第二天的价格为b。第一天有促销活动,每买m千克物品,可以额外获得1千克物品。问最少花费多少可以获得至少n千克的物品。 思路:分类讨论&…...
】7-2 Reversing Linked List)
【PTA Data Structures and Algorithms (English)】7-2 Reversing Linked List
Given a constant K and a singly linked list L, you are supposed to reverse the links of every K elements on L. For example, given L being 1→2→3→4→5→6, if K3, then you must output 3→2→1→6→5→4; if K4, you must output 4→3→2→1→5→6. Input Specif…...

Jetpack Compose 学习汇总
关于 Jetpack Compose 的学习本想只是简单的快速学习一下,结果万万没想到,竟然一下子折腾了好几个月。。。 下面将之前记录的 Jetpack Compose 相关的学习博文进行一个汇总链接整理,方便我以后自己查阅,也希望能帮到一些有正在学…...
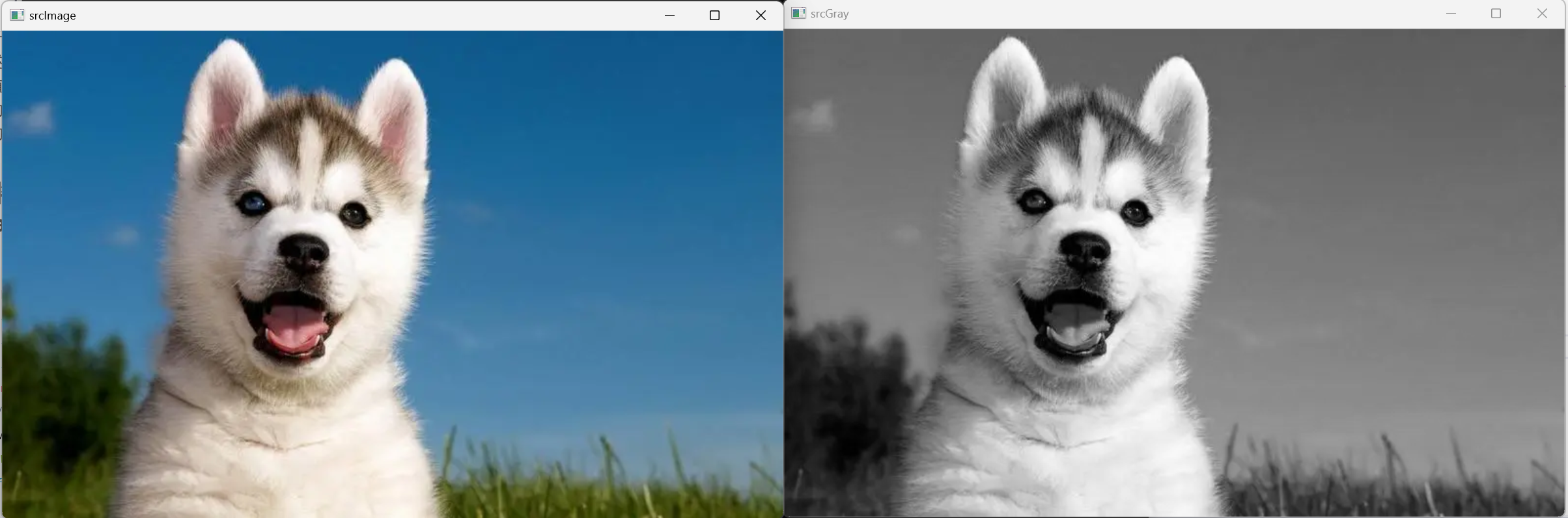
【OpenCv】c++ 图像初级操作 | 图像灰度化
文章目录一、图像1、图像信息2、图像种类1)二值图像:2)灰度图:3)彩色图:二、图像转化1、分离彩色图三个通道2、图像灰度化处理一、图像 1、图像信息 Q:图像在计算机中怎么储存? A:…...

VIT(vision transformer)onnx模型解析
背景:transformer在CV领域的应用论文下载链接:https://arxiv.org/abs/2010.11929Pytorch实现代码: pytorch_classification/vision_transformer(太阳花的小绿豆博主实现的代码)有一些大神在研究关于CNNtransformer或者纯用transformer实现。原…...
红黑树的介绍和实现
文章目录1. 红黑树1.1 红黑树的概念1.2 红黑树的性质1.3 红黑树节点的定义1.4 红黑树的插入1.5 红黑树的验证1.6 红黑树与AVL树的比较1. 红黑树 1.1 红黑树的概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以…...

C/C++每日一练(20230310)
目录 1. 用栈实现队列 ★★ 2. 单词搜索 II ★★★ 3. 直线上最多的点数 ★★★ 1. 用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: v…...

Go语言基础知识
常量//定义方式 const a int12;//指定变量类型 const b12;//不指定变量类型,由编译时go自动确认 const(//多行定义方式a12b23 ) //说到const,不得不得不提到的一个参数iota,初始值为0,在用const多行定义的方式中, 如果第一行定义了…...
案例06-没有复用思想的接口和sql--mybatis,spring
目录一、背景二、思路&方案问题1优化问题2优化三、总结四、升华一、背景 写这篇文章的目的是通过对没有复用思想接口的代码例子优化告诉大家,没有复用思想的代码不要写,用这种思维方式和习惯来指导我们写代码。 项目中有两处没有复用思想代码&#…...

如何将项目部署到服务器:从选择服务器到维护应用程序的全流程指南
将项目部署到服务器是一个重要的技能,对于开发人员来说,它是必不可少的。在本文中,我将介绍一些关于如何将项目部署到服务器的最佳实践。一、选择服务器在部署项目之前,你需要先选择一个适合你的服务器。如果你已经有一个可用的服…...

怎么做才能不丢消息?
现在主流的消息队列产品都提供了非常完善的消息可靠性保证机制,可以做到在消息传递的过程中,即使发生网络中断或者硬件故障,也能确保消息的可靠传递、不丢消息。 绝大部分丢消息的原因都是由于开发者不熟悉消息队列,没有正确使用…...

前端基础(十六)_数组对象
数组对象 1、创建数组 // 字面量创建const arr [1, 2, 3, 4, 5, 6]// 构造函数创建const arr2 new Array(1, 2, 3, 4, 5, 6)const arr3 Array(1, 2, 3, 4, 5, 6)2.push (从数组末尾添加元素) a.数组.push(要添加进数组的数组项) b.作用:将要添加的数组项 添加到…...

数据结构-带头双向循环链表
前言: 链表有很多种,上一章结,我复盘了单链表,这一章节,主要针对双链表的知识点进行,整理复盘,如果将链表分类的话,有很多种,我就学习的方向考察的重点,主要…...

3 问 6 步,极狐GitLab 帮助企业构建高效、安全、合规的 DevSecOps 文化
本文来源:about.gitlab.com 作者:Vanessa Wegner 译者:极狐(GitLab) 市场部内容团队 🔒 安全为何重要?此前,我们分享了: 1. 2023年DevOps发展趋势👉重磅!GitLab 提出五大…...
知多少)
SPA(单页应用)知多少
单页面应用程序将所有的活动局限于一个Web页面中,在该Web页面初始化时加载相应的HTML、JavaScript 和 CSS。一旦页面加载完成,单页面应用不会因为用户的操作而进行页面的重新加载或跳转。取而代之的是利用 JavaScript 动态的变换HTML的内容,从…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
