数据结构:哈夫曼树及其哈夫曼编码
目录
1.哈夫曼树是什么?
2.哈夫曼编码是什么?
3.哈夫曼编码的应用
4.包含头文件
5.结点设计
6.接口函数定义
7.接口函数实现
8.哈夫曼编码测试案列
哈夫曼树是什么?
哈夫曼树(Huffman Tree)是一种特殊的二叉树,由David A. Huffman在1952年发明的,用于数据压缩领域。哈夫曼树是一种最优的二叉树,因为它具有最小的加权路径长度。这里的“最优”是指在给定的一组权重(通常是字符出现频率)下,哈夫曼树的加权路径长度(即树中所有叶节点的权重乘以其到根节点的距离)是最小的,以下是哈夫曼树的特点:
1.完全二叉树:除了最后一层外,每一层都是满的
2.加权路径长度最小:所有叶节点的权重乘以其到根节点的距离之和是最小的
3.每个节点都有权重:叶节点代表单个字符,非叶节点代表字符的集合
哈夫曼编码是什么?
哈夫曼编码是一种使用哈夫曼树进行编码的方法。它将每个字符映射为一个唯一的二进制串,这些二进制串的长度不同,且是根据字符出现频率来确定的。频率越高的字符,其编码越短;频率越低的字符,其编码越长。这种编码方式可以有效地减少数据的存储空间或传输时间。实现哈夫曼编码的步骤如下:
1.统计字符频率:首先统计数据集中每个字符出现的频率
2.构建哈夫曼树:
1.将每个字符及其频率作为叶子节点放入优先队列(通常是最小堆)
2.从队列中取出两个权重最小的节点,创建一个新的内部节点,其权重为这两个节点权重之和
3.将新节点重新加入队列。重复上述步骤,直到队列中只剩下一个节点,这个节点就是哈夫曼树的根节点
3.生成编码:从根节点开始,向左子树走标记为0,向右子树走标记为1,直到到达叶节点,此时叶节点对应的字符的路径标记就是其哈夫曼编码
哈夫曼编码的应用
哈夫曼编码是一种非常实用的编码技术,它通过利用数据的内在特性来优化存储和传输效率:
1.数据压缩:用于无损数据压缩,特别是在文本压缩中非常有效。
2.文件压缩:如ZIP文件格式就使用了哈夫曼编码。
3.通信协议:在某些通信协议中,用于减少传输数据的大小。
包含头文件
#include<stdio.h>
#include<stdlib.h>
#include<string.h>结点设计
#define Initsize 100
typedef int Elemtype;
int Node[Initsize][2]; //定义二维数组Node存储输入的字符和字符所含的权值
int NodeValue[Initsize]; //定义一维数组NodeValue存储经排序过的字符的权值
int Hand = 0; //定义整形变量Hand作为数组NodeValue的头指针
int CodeHead = 0; //定义int类型变量CodeHead作为指针数组Code的头指针typedef struct HTree {Elemtype value; //存储结点权值Elemtype Lvalue, Rvalue; //存储孩子标识struct HTree* lchild; //存储左孩子树struct HTree* rchild; //存储右孩子树
}HTree,*HfmTree;HfmTree Head; //定义全局变量Head作为哈夫曼树的根节点指针
HfmTree Code[Initsize]; //定义HTree类型的指针数组Code,存储结点的地址接口函数定义
void InitHTree(HfmTree& A); //用于初始化哈夫曼树
void InsertNode(int A); //用于输入字符和其权值
void SortNodeV(int A); //用于对输入的权值进行排序
void InitLHfm(HfmTree& A); //用于哈夫曼树的左子树进行初始化并赋值
void InitRHfm(HfmTree& A); //用于哈夫曼树的右子树进行初始化并赋值
void InsertHTree(HfmTree& A,int B); //用于创建哈夫曼树
void PostOrder(HfmTree A); //用于对哈夫曼树进行后序遍历
void InputBTree(HfmTree A); //用于对哈夫曼树的结点权值输出
void SeekHTreeL(HfmTree A, int B); //用于单独寻找哈夫曼树的左子树的字符及权值
void SeekHTreeR(HfmTree A, int B); //用于寻找哈夫曼树的右子树的字符及权值
void InputHfmCode(HfmTree A,int B); //用于输出哈夫曼编码
void InitRootHfm(HfmTree& A,HfmTree &B,HfmTree &C); //用于对哈夫曼树的根结点进行初始化并赋值接口函数实现
void InputHfmCode(HfmTree A,int B) { //用于输出哈夫曼编码int i,j;while (A != NULL) { //对哈夫曼树的左子树进行进栈操作Code[CodeHead] = A;A = A->lchild;CodeHead++;}printf("\n");SeekHTreeL(A, B); //使用函数SeekHtreeL对其哈夫曼树进行寻找左子树的字符及权值for (i = 1; i < CodeHead; i++) {printf("%d", Code[i]->Lvalue); //对栈里结点所含的Lvalue进行输出(从根结点开始输出其含有的LvaLue)}CodeHead--; //出栈操作while (CodeHead != 0) { //判断栈是否为空printf("\n");SeekHTreeR(A, B); //使用函数SeekHTreeR对其哈夫曼树进行寻找右子树的字符及权值for (i = 0; i <= CodeHead - 1; i++) { //对栈里结点所含的Lvalue进行输出(从根结点开始输出其含有的LvaLue)if (i == CodeHead - 1) { //若为栈尾结点则输出其右子树printf("%d", Code[i]->Rvalue); break;}printf("%d", Code[i]->Lvalue);}CodeHead--; //出栈操作}
}void SeekHTreeR(HfmTree A, int B) { //用于寻找哈夫曼树的右子树的字符及权值int i,j;for (i = CodeHead - 1; i >= 0; i++){ //遍历栈if (i == CodeHead-1) { //判断是否为栈的倒数第二个结点(跟定义的结点的有关)for (j = 0; j < B; j++) { //遍历存储字符及权值的数组,寻找对应的字符和权值if (Node[j][1] == Code[i]->rchild->value) {Node[j][1] = -1; //未防止字符不一样,但权值相同的出现,造成输出哈夫曼编码错误printf("%c的哈夫曼编码为:", Node[j][0]);break; }}}break; }
}void SeekHTreeL(HfmTree A, int B){ //用于单独寻找哈夫曼树的左子树的字符及权值int i,j;for (i = 0; i < CodeHead; i++) { //遍历栈if (i == CodeHead - 1) { //判断是否为栈的倒数第二个结点(跟定义的结点的有关)for (j = 0; j < B; j++) { //遍历存储字符及权值的数组,寻找对应的字符和权值if (Node[j][1] == Code[i]->value) { Node[j][1] = -1; //未防止字符不一样,但权值相同的出现,造成输出哈夫曼编码错误printf("%c的哈夫曼编码为:", Node[j][0]);break;}}}}
}void InputBTree(HfmTree A) { //用于对哈夫曼树的结点权值输出 printf("%d ", A->value);
}void PostOrder(HfmTree A) { //用于对哈夫曼树进行后序遍历 if (A != NULL) {PostOrder(A->lchild); PostOrder(A->rchild); InputBTree(A); }
}void InsertHTree(HfmTree& A,int B) {//用于创建哈夫曼树if(Hand<B-1){ //判断是否已将所有字符及权值进行构建对应的哈夫曼树的结点if (A == NULL) { HfmTree Q = (HTree*)malloc(sizeof(HTree)); HfmTree W = (HTree*)malloc(sizeof(HTree)); InitLHfm(Q); //使用函数InitLHfm对其左子树初始化Hand++;InitRHfm(W); //使用函数InitRHfm对其右子树初始化InitRootHfm(A, Q, W); //使用函数InitRootHfm对其根结点初始化Head = A; //更新哈夫曼树的头指针的指向InsertHTree(A, B); }else {HfmTree Q = (HTree*)malloc(sizeof(HTree)); HfmTree W = (HTree*)malloc(sizeof(HTree)); Hand++;InitRHfm(Q); //使用函数InitRHfm对其右子树初始化InitRootHfm(W, A, Q); //使用函数InitRootHfm对其根结点初始化Head = W;InsertHTree(W, B);}}
}void InitRootHfm(HfmTree& A, HfmTree& B, HfmTree& C) {//用于对哈夫曼树的根结点进行初始化并赋值A = (HTree*)malloc(sizeof(HTree));A->value = B->value + C->value; //根结点的权值为两个子结点的权值之和A->Lvalue = 1; //添加左子树标识A->Rvalue = 0;A->lchild = B; //添加根结点指向的左子树A->rchild = C; //添加根结点指向的右子树printf("新建的根结点的权值数据为%d\n", A->value);
}void InitRHfm(HfmTree& A) { //用于哈夫曼树的右子树进行初始化并赋值A->value = NodeValue[Hand]; //对结点所含的权值进行更新A->Lvalue = 0;A->Rvalue = 1; //添加右子树标识A->lchild = NULL; A->rchild = NULL;printf("新建的右孩子的权值数据为%d\n", A->value);
}void InitLHfm(HfmTree& A) { //用于哈夫曼树的左子树进行初始化并赋值A->value = NodeValue[Hand]; //对结点所含的权值进行更新A->Lvalue = 1; //添加左子树标识A->Rvalue = 0;A->lchild = NULL;A->rchild = NULL;printf("新建的左孩子的权值数据为%d\n", A->value);
}void SortNodeV(int A) { //用于对输入的权值进行排序int i, j, Q;for (i = 0; i < A - 1; i++) { //冒泡排序for (j = 0; j < A - 1 - i; j++)if (NodeValue[j] > NodeValue[j + 1]) {Q = NodeValue[j];NodeValue[j] = NodeValue[j + 1];NodeValue[j + 1] = Q;}}
}void InsertNode(int A) { //用于输入字符和其权值int i, j;char Q;for (i = 0; i < A; i++) {j = 0;printf("请输入结点的字符");getchar(); //清除缓冲区,防止赋值脏数据Q=getchar();Node[i][j] = (int) Q;j++;printf("请输入结点的权值");scanf_s("%d", &Node[i][j]);NodeValue[i] = Node[i][j];}
}void InitHTree(HfmTree& A) { //用于初始化哈夫曼树A = NULL;printf("初始化哈夫曼树成功\n");
}哈夫曼编码测试案列
void main() {int NodeSize,i;HfmTree X;InitHTree(X);printf("请问需要输入多少个字符");scanf_s("%d", &NodeSize);InsertNode(NodeSize);SortNodeV(NodeSize);InsertHTree(X, NodeSize);printf("创建哈夫曼树成功\n");printf("后序遍历的哈夫曼树为:");PostOrder(Head);printf("\n");InputHfmCode(Head,NodeSize);
}相关文章:

数据结构:哈夫曼树及其哈夫曼编码
目录 1.哈夫曼树是什么? 2.哈夫曼编码是什么? 3.哈夫曼编码的应用 4.包含头文件 5.结点设计 6.接口函数定义 7.接口函数实现 8.哈夫曼编码测试案列 哈夫曼树是什么? 哈夫曼树(Huffman Tree)是一种特殊的二叉树…...
微信如何防止被对方拉黑删除?一招教你解决!文末附软件!
你一定不知道,微信可以防止被对方拉黑删除,秒变无敌。只需一招就能解决!赶快来学!文末有惊喜! 惹到某些重要人物(比如女朋友),被删除拉黑一条龙,那真的是太令人沮丧了&a…...

jar增量打包
jar增量打包 Linux环境下: 1.解压缩 jar -xvf jarname.jar(解压)2.打包 这时可以把要替换的lib包的内容粘帖进去,然后重新打jar包 jar -cvf0M jarname.jar .(重新压缩,-0是主要的)jar命令: …...

智慧医院物联网建设-统一管理物联网终端及应用
近年来,国家卫健委相继出台的政策和评估标准体系中,都涵盖了强化物联网建设的内容。物联网建设已成为智慧医院建设的核心议题之一。 作为医院高质量发展的关键驱动力,物联网的顶层设计与网络架构设计规划,既需要结合现代信息技术的…...

Debian的常用命令
Debian作为一个稳定、安全且高效的Linux发行版,被广泛应用于服务器和桌面操作系统中。对于系统管理员和开发者来说,熟练掌握Debian的常用命令能够大大提升工作的效率和系统的管理水平。本文将详细介绍一些常见且实用的Debian命令,帮助新手更好地管理和操作Debian系统。 系统…...

矩阵1-范数与二重求和的求和可交换
矩阵1-范数与二重求和的求和可交换 1、矩阵1-范数 A [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] A \begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots …...

Python笔记 - *args和**kwargs
探索Python的*args和**kwargs 在Python中,函数可以接受任意数量的参数,而这要归功于*args和**kwargs的强大功能。这两个特性使得函数在处理不同数量的输入时变得更加灵活和高效。在这篇博客中,我们将详细介绍*args和**kwargs,并展…...

微信小程序实现图片转base64
在微信小程序中,图片转base63可以引入第三方插件; 也可以通过下边的方法转base64。 转换方法: imgToBase64(filePath) {return new Promise((resolve, reject) > {let baseFormat data:image/png;base64,let base64 wx.getFileSystem…...

os和os.path模块
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 目录也称文件夹,用于分层保存文件。通过目录可以分门别类地存放文件。我们也可以通过目录快速找到想要的文件。在Python中,并…...
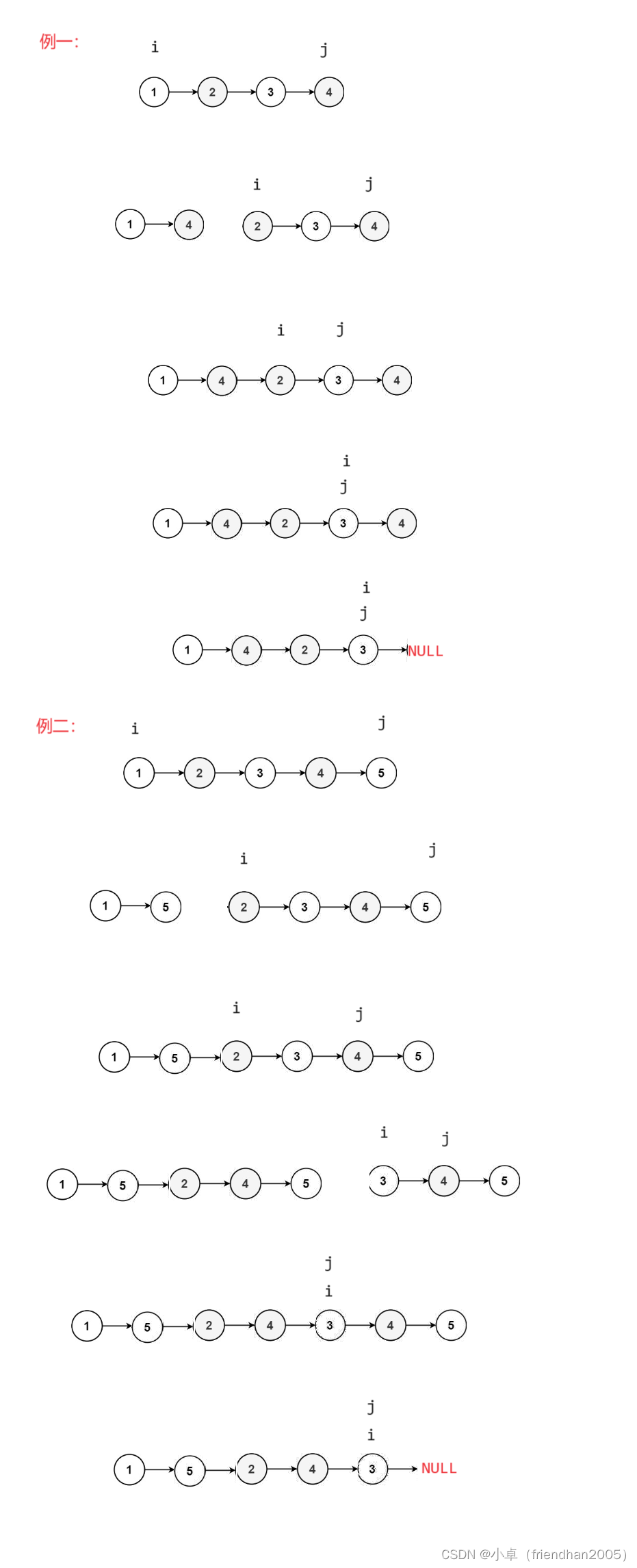
链表题目练习----重排链表
这道题会联系到前面写的一篇文章----快慢指针相关经典问题。 重排链表 指针法 这道题乍一看,好像有点难处理,但如果仔细观察就会发现,这道题是查找中间节点反转链表链表的合并问题,具体细节有些不同,这个在反装中间链…...

【杂记-浅谈XSS跨站脚本攻击】
一、什么是XSS? XSS,Cross-site Scripting,跨站脚本攻击,是一种典型的Web程序漏洞利用攻击,攻击者利用Web程序对用户输入检查不足的漏洞将可执行恶意脚本注入网站或Web应用,当用户访问网页时触发恶意脚本的…...
VMware虚拟机与MobaXterm建立远程连接失败
VMware虚拟机与MobaXterm建立远程连接失败 首先可以检查一下是不是虚拟机的ssh服务并不存在 解决方法: 1.更新镜像源 yum -y update 这个过程会有点久,请耐心等待 2.安装ssh yum install openssh-server 3.启动ssh systemctl restart sshd 4.查…...

mysql undolog管理
在MySQL中,Undo Log(撤销日志)用于支持事务的回滚和MVCC(多版本并发控制)。为了避免Undo Log不断增长,影响系统性能,需要进行合理的清理。MySQL的Undo Log清理策略主要依赖于系统的配置参数和后…...

【Linux】进程2——管理概念,进程概念
1.什么是管理? 那在还没有学习进程之前,就问大家,操作系统是怎么管理进行进程管理的呢? 很简单,先把进程描述起来,再把进程组织起来! 我们拿大学为例子 最典型的管理者——校长最典型的被管理…...

【C++】植物大战僵尸杂交版自动存档——防闪退存档消失
植物大战僵尸杂交版现已更新到v2.0.88,闪退问题还是偶有发生,参考网上现有的方案,简单实现了一个。 原理就是监控存档目录的文件变化,一旦有新的存档,则将其备份。如发生闪退,则还原备份即可。 原目录&…...
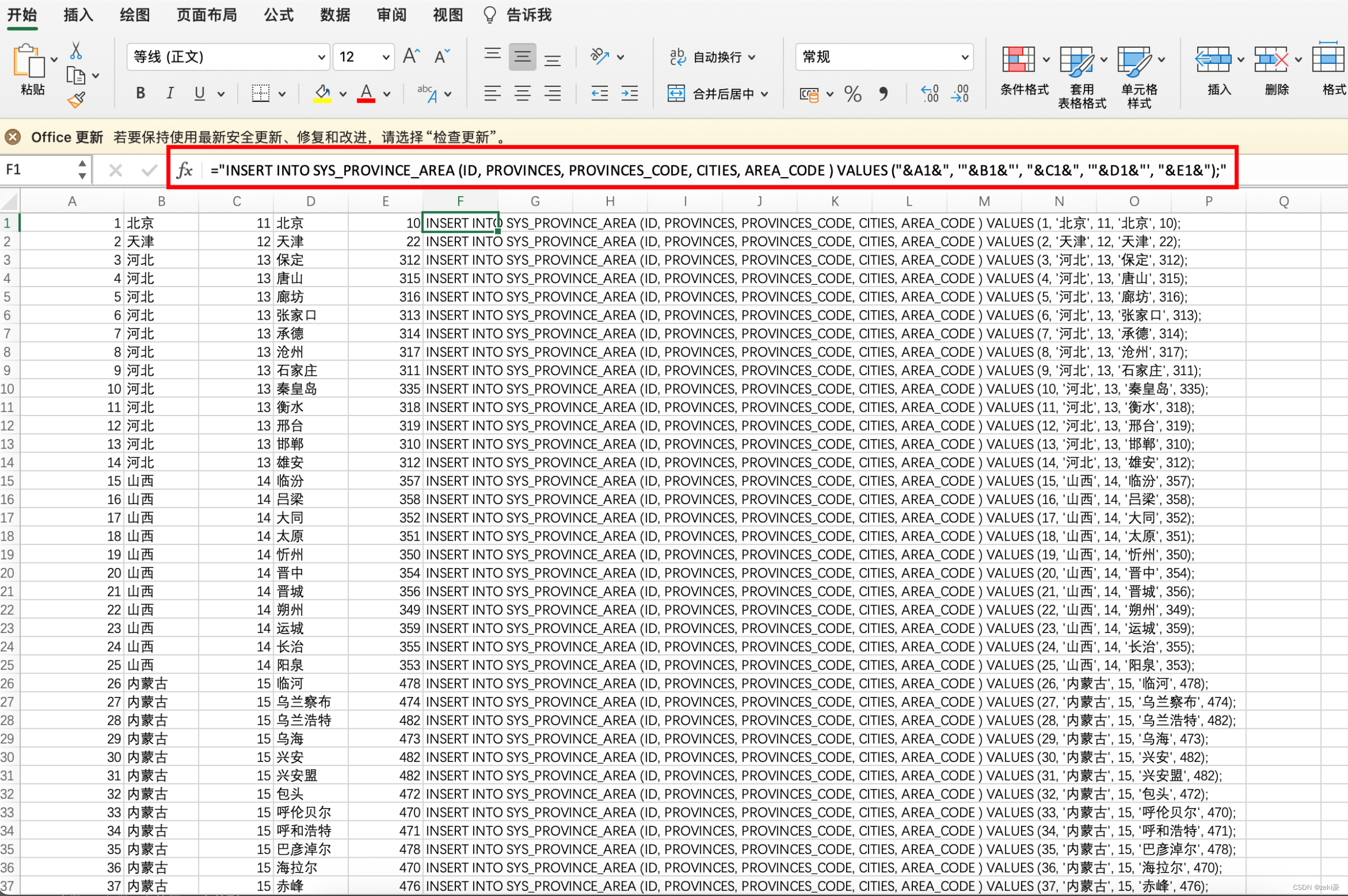
通过Excel,生成sql,将A表数据插入B表
文章目录 投机取巧的方式,进行表数据初始化通过navicat搜索A表数据,然后复制进excel中通过excel的函数方式,将该批量数据自动生成插入B表的sql语句然后一次性拷贝生成的sql语句,放进navicat中一次执行,直接完成数据初始化...

如何在MySQL中实现upsert:如果不存在则插入?
目录 1 使用 REPLACE 2 使用 INSERT ... ON DUPLICATE KEY UPDATE 使用 INSERT IGNORE 有效会导致 MySQL 在尝试执行语句时忽略执行错误 INSERT 。这意味着 包含 索引或 字段 INSERT IGNORE 中重复值的语句 不会 产生错误,而只是完全忽略该特定 命令。其明显目的是…...
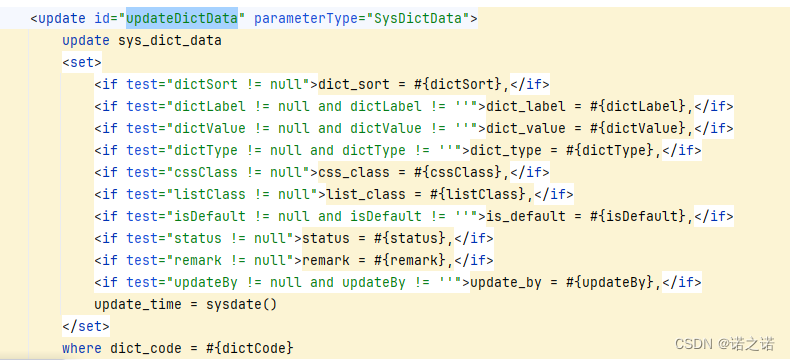
MyBatis中 set标签
1、set标签特点: set标签用于更新语句中set标签解析为set关键字set可以去除跟新语句中无用的逗号通常是和if标签一起使用 2、set标签的使用 编写接口方法编写sql语句 注意 当set标签中有条件成立时就会附加set关键字,字段为null时该列不会被更新。se…...

mysql自带分页
select 查询列表 from 表 limit offset,pagesize; offset代表的是起始的条目索引,默认从0开始size代表的是显示的条目数offset(n-1)*pagesize -- 第-页 limit 0 5 -- 第二页 limit 5,5 -- 第三页 limit 10,5 -- 第n页limit(n-1)*pagesize,pagesize -- pages…...

小学一年级数学上册,我终于学完了
目录 一、背景二、过程1.我对课程中的一些知识的思考2.我对于产品的思考3.我对自己儿子与知识产品结合的思考4.产品反馈的那些有意思的数据 三、总结 一、背景 简约而不简单,即是曾经的再现,也是未来的延伸,未来已来,就在脚下。 …...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...

使用python进行图像处理—图像变换(6)
图像变换是指改变图像的几何形状或空间位置的操作。常见的几何变换包括平移、旋转、缩放、剪切(shear)以及更复杂的仿射变换和透视变换。这些变换在图像配准、图像校正、创建特效等场景中非常有用。 6.1仿射变换(Affine Transformation) 仿射变换是一种…...

Qt 按钮类控件(Push Button 与 Radio Button)(1)
文章目录 Push Button前提概要API接口给按钮添加图标给按钮添加快捷键 Radio ButtonAPI接口性别选择 Push Button(鼠标点击不放连续移动快捷键) Radio Button Push Button 前提概要 1. 之前文章中所提到的各种跟QWidget有关的各种属性/函数/方法&#…...

八、【ESP32开发全栈指南:UDP客户端】
1. 环境准备 安装ESP-IDF v4.4 (官方指南)确保Python 3.7 和Git已安装 2. 创建项目 idf.py create-project udp_client cd udp_client3. 完整优化代码 (main/main.c) #include <string.h> #include "freertos/FreeRTOS.h" #include "freertos/task.h&…...
