多源最短路径算法–Floyd算法
多源最短路径算法–Floyd算法
Floyd算法是为了求出每一对顶点之间的最短路径
它使用了动态规划的思想,将问题的求解分为了多个阶段
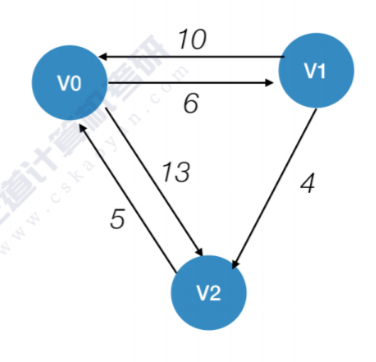
先来个例子,这是个有向图
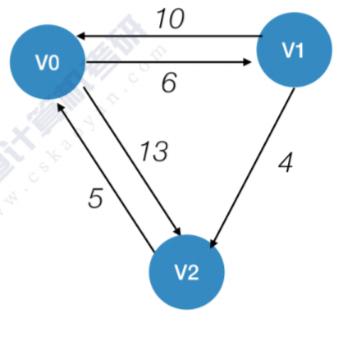
Floyd算法的运行需要两个矩阵
最短路径矩阵
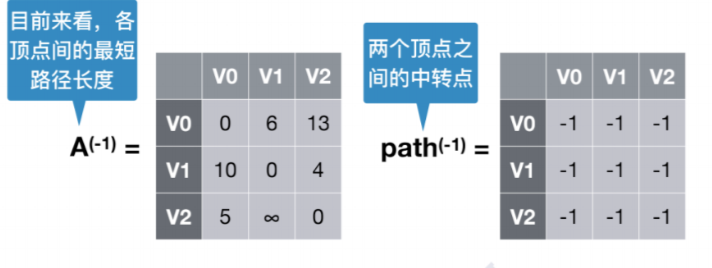
从当前这个状态看各顶点间的最短路径长度
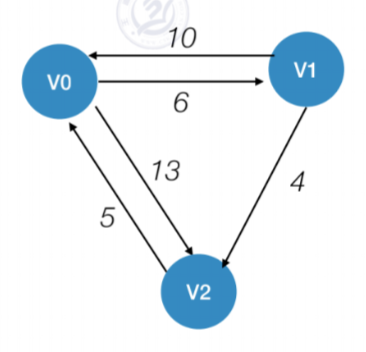
例如初始状态
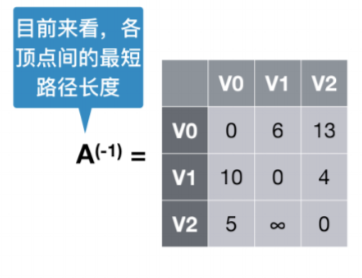
可以看出这是该有向图的邻接矩阵
顶点之间中转点矩阵
初始状态都没有中转点
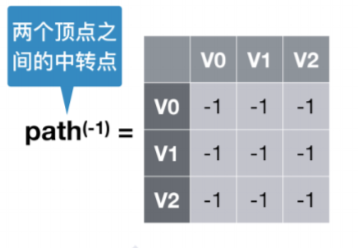
引入中转点
A(k-1)代表引入顶点k-1时,各个顶点的最短路径状态
path(k-1)代表引入顶点k-1后,各个顶点的最短路径需要经过哪个结点

判断顶点i到顶点j,如果经过顶点k,是否会更短?
如果更短,改变A(k-1)数组中i结点到j结点的最短路径,同时更改path(k)数组,表明经过顶点k,顶点i到顶点j路径更短
- 允许在V0中转,计算出当前的最短路径
顶点2到顶点1
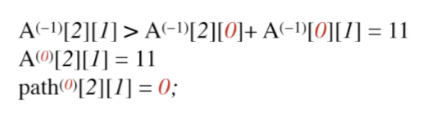
可以看到原来顶点2到顶点1是没有路径的,通过V0之后,最短路径变为11,那么更新A(0)数组,A(0)数组代表引入V0之后个顶点之间的最短路径,同是更新path(0)数组,代表V2到V1经过了V0

- 允许在V0,V1中转,计算出当前的最短路径
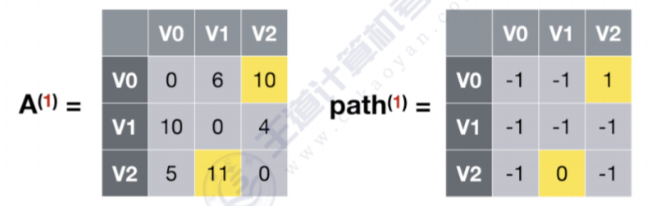
顶点0到顶点2
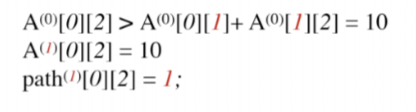
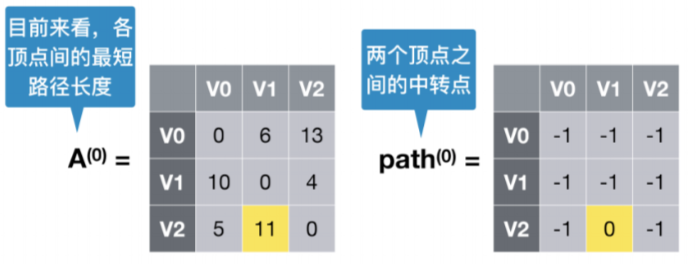
可以看到原来顶点0到顶点2的距离是13,通过V1之后,最短路径变为10,那么更新A(1)数组,A(1)数组代表引入V1之后个顶点之间的最短路径,同是更新path(1)数组,代表V0到V2经过了V1
- 允许在V0,V1,V2中转,计算出当前的最短路径
顶点1到顶点0
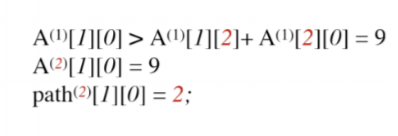

可以看到原来顶点1到顶点0的距离是10,通过V1之后,最短路径变为9,那么更新A(2)数组,A(2)数组代表引入V2之后个顶点之间的最短路径,同是更新path(2)数组,代表V1到V0经过了V2
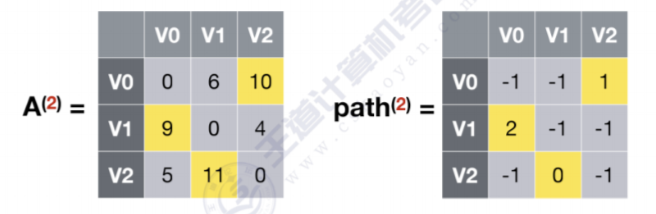
- 最终结果

- 核心代码

再看一个新的例子
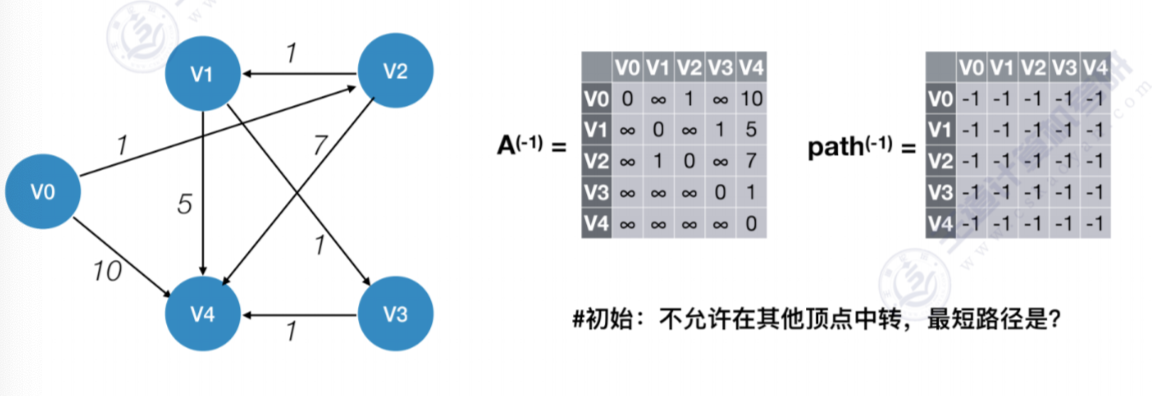
- 允许在V0中转,k=0

所有结点之间都不能通过V0获得更短的路径,故不更新A(0)数组和path(0)数组
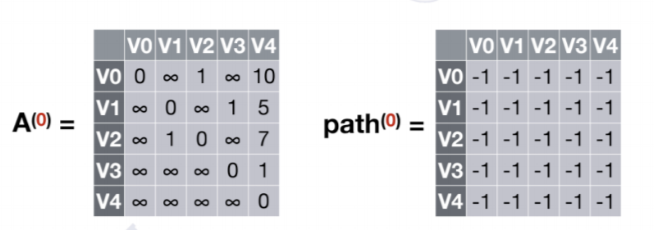
- 允许在V0,V1中转,k=1


V2到V3和V2到V4经过V0,V1中转有更短的路径,故更新A(1)数组和path(1)数组
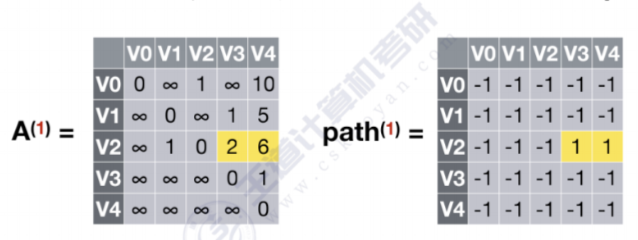
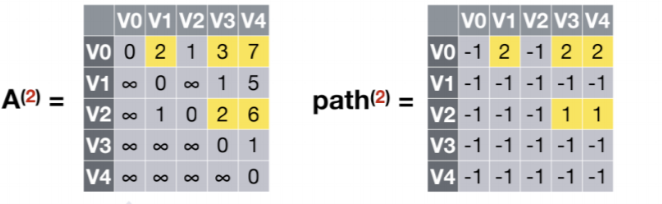
- 允许在V0,V1,V2中转,k=2


V0到V1,V0到V3,V0到V4经过V0,V1,V2中转有更短的路径,故更新A(2)数组和path(2)数组
- 允许在V0,V1,V2,V3中转,k=3


V0到V4,V1到V4,V2到V4经过V0,V1,V2,V3中转有更短的路径,故更新A(3)数组和path(3)数组
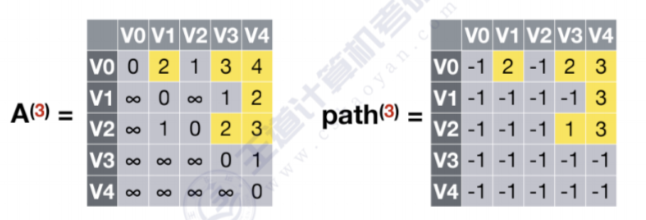
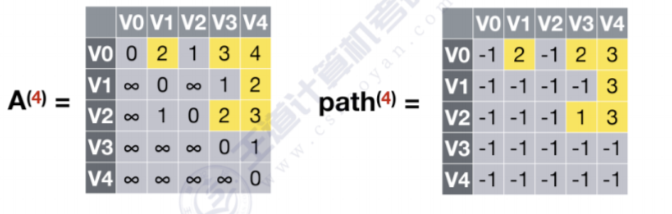
- 允许在V0,V1,V2,V3,V4中转,k=4

所有结点之间都不能通过V4获得更短的路径,故不更新A(4)数组和path(4)数组
注意
- Floyd算法不能解决带有“负权回路”的图,这种图可能没有最短路径
相关文章:

多源最短路径算法–Floyd算法
多源最短路径算法–Floyd算法 Floyd算法是为了求出每一对顶点之间的最短路径 它使用了动态规划的思想,将问题的求解分为了多个阶段 先来个例子,这是个有向图 Floyd算法的运行需要两个矩阵 最短路径矩阵 从当前这个状态看各顶点间的最短路径长度 例…...
使用Redis缓存实现短信登录逻辑,手机验证码缓存,用户信息缓存
引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId></dependency> 加配置 spring:redis:host: 127.0.0.1 #redis地址port: 6379 #端口password: 123456 #密码…...

探索未来制造,BFT Robotics引领潮流
“买机器人,上BFT” 在这个快速变化的时代,创新和效率是企业发展的关键。BFT Robotics,作为您值得信赖的合作伙伴,专注于为您提供一站式的机器人采购和自动化解决方案。 产品系列: 协作机器人:安全、灵活、…...
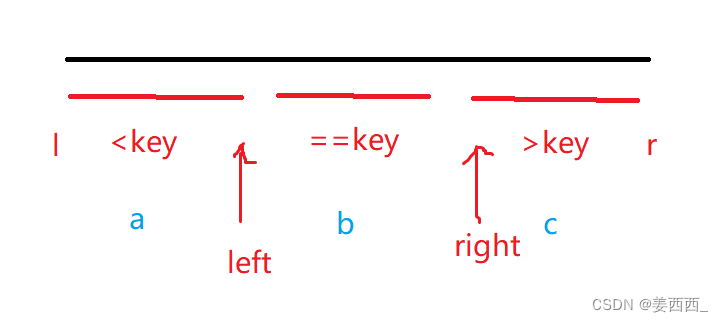
数组中的第K个最大元素 ---- 分治-快排
题目链接 题目: 分析: 这道题很明显是一个top-K问题, 我们很容易想到用堆排序来解决, 堆排序的时间复杂度是O(N*logN), 不符合题意, 所以我们可以用另一种方法:快速选择算法, 他的时间复杂度为O(N)快速选择算法, 其实是基于快排, 进行修改而成, 我们还是使用将"将数组分…...

函数或变量 ‘tfrstft‘ 无法识别
参考博客 Matlab时频工具箱tftb下载及安装_tftb工具箱-CSDN博客 解决。...

在推荐四款软件卸载工具,让流氓软件无处遁形
Revo Uninstaller Revo Uninstaller是一款电脑软件、浏览器插件卸载软件,目前已经有了17年的历史了。可以扫描所有window用户卸载软件后的残留物,并及时清理,避免占用电脑空间。 Revo Uninstaller可以通过命令行卸载软件,可以快速…...
)
「前端+鸿蒙」核心技术HTML5+CSS3(十一)
1、CSS3 简介 CSS3 是层叠样式表的最新标准,它引入了许多新特性来增强网页的表现力。CSS3 不仅增强了现有CSS属性的功能,还引入了新的布局方式、动画、渐变、阴影、边框效果等。 2、CSS3 长度单位 CSS3 引入了一些新的单位,包括但不限于: vw(视口宽度的百分比)vh(视口…...

【高频】如何优化一个SQL语句
使用合适的索引:确保查询中涉及的字段上有合适的索引,避免全表扫描。可以通过 EXPLAIN 命令来查看查询执行计划,判断是否使用了索引。 避免使用通配符查询:尽量避免在查询条件中使用通配符(如 %)ÿ…...
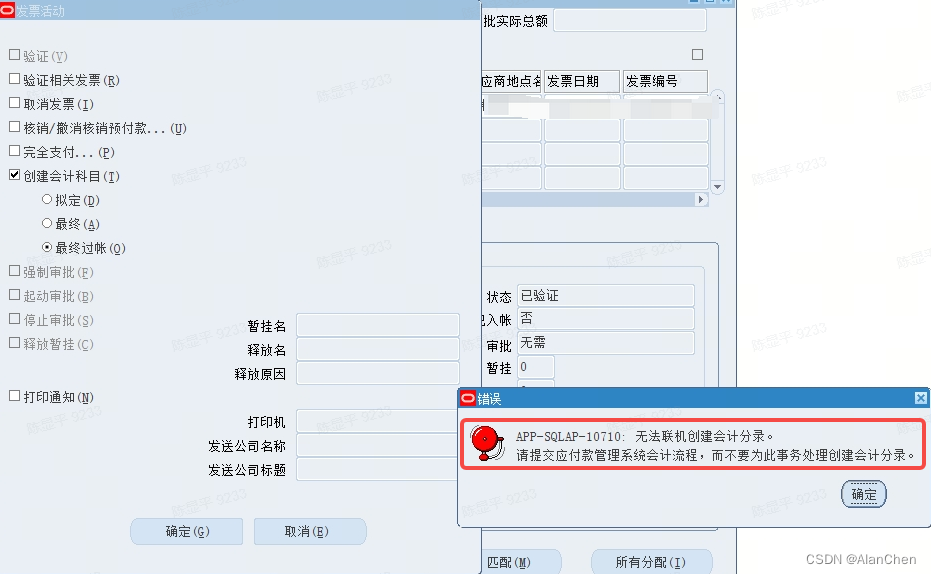
Oracle EBS AP发票创建会计科目提示:APP-SQLAP-10710:无法联机创建会计分录
系统版本 RDBMS : 12.1.0.2.0 Oracle Applications : 12.2.6 问题症状: 提交“创建会计科目”请求提示错误信息如下: APP-SQLAP-10710:无法联机创建会计分录。 请提交应付款管理系统会计流程,而不要为此事务处理创建会计分录解决方法 数据修复SQL脚本: UPDATE ap_invoi…...

T-Pot多功能蜜罐实践@debian12@FreeBSD
T-Pot介绍 T-Pot是一个集所有功能于一身的、可选择分布式的多构架(amd64,arm64)蜜罐平台,支持20多个蜜罐和很多可视化选项,使用弹性堆栈、动画实时攻击地图和许多安全工具来进一步改善欺骗体验。GitHub - telekom-sec…...

Sed流编辑器总结
sed 是 Unix 和 Linux 系统中的一个强大的流编辑器。它用于对文本进行基本的修改和处理。以下是关于 sed 的详细解说,包括其基本语法,常见用法和一些高级用法。 基本语法 sed [选项] 命令 输入文件常见选项 -e:指定要执行的 sed 命令。-f&a…...

智合同丨AIGC如何助力合同智能应用
#AIGC #合同智能应用 #智合同 AIGC,即人工智能生成内容技术(Artificial Intelligence Generated Content),近期在各个领域发展可谓是如火如荼,那么它在合同智能应用方面可以提供哪些助力? 让我们和智合…...

CSRF 令牌的生成过程和检查过程
在 Django 中,CSRF 令牌的生成和检查过程是通过 Django 的 CSRF 中间件 (CsrfViewMiddleware) 和模板标签 ({% csrf_token %}) 自动处理的。以下是详细的生成和检查过程: CSRF 令牌的生成过程 用户访问页面: 当用户第一次访问页面时,Django 会为用户创建一个会话。如果用户…...

计算机网络学习记录 网络层 Day4(下)
计算机网络学习记录 网络层 Day4 (下) 你好,我是Qiuner. 为记录自己编程学习过程和帮助别人少走弯路而写博客 这是我的 github https://github.com/Qiuner ⭐️ gitee https://gitee.com/Qiuner 🌹 如果本篇文章帮到了你 不妨点个赞吧~ 我…...
3、前端本地环境搭建
前端本地环境搭建 安装node [node下载地址] https://nodejs.org/en/download/prebuilt-installer 选择LTS的版本进行下载 下载后直接双击点击,选择自己想要安装到的目录一直点下一步即可(建议不要安装到c盘) 安装完成后配置环境变量&am…...

Python爬取城市空气质量数据
Python爬取城市空气质量数据 一、思路分析1、寻找数据接口2、发送请求3、解析数据4、保存数据二、完整代码一、思路分析 目标数据所在的网站是天气后报网站,网址为:www.tianqihoubao.com,需要采集武汉市近十年每天的空气质量数据。先看一下爬取后的数据情况: 1、寻找数据…...

【MyBatisPlus条件构造器】
文章目录 什么是条件构造器?使用步骤1. 引入 MyBatisPlus 依赖2. 创建实体类3. 使用条件构造器查询4. 执行查询 示例代码 什么是条件构造器? 条件构造器是 MyBatisPlus 提供的一种灵活的查询条件设置方式,它可以帮助开发者构建复杂的查询条件…...

容器多机部署eureka及相关集群服务出现 Request execution failed with message: AuthScheme is null
预期部署方案:两个eureka三个相关应用 注册时应用出现:Request execution failed with message: Cannot invoke “Object.getClass()” because “authScheme” is null,一开始认为未正确传递eureka配置的账户密码,例:…...

Qt Graphics View Framework 使用教程
欢迎来到 Qt Graphics View Framework 的世界!本教程将引导您了解这一强大工具的基础知识,并教您如何开始使用它来创建丰富的 2D 图形界面。无论您是编程新手还是经验丰富的开发者,本教程都将帮助您快速上手。 基本概念 Qt Graphics View F…...
【调试笔记-20240606-Linux-为 OpenWrt 的 nginx 服务器添加Shell CGI 支持】
调试笔记-系列文章目录 调试笔记-20240606-Linux-为 OpenWrt 的 nginx 服务器添加Shell CGI 支持 文章目录 调试笔记-系列文章目录调试笔记-20240606-Linux-为 OpenWrt 的 nginx 服务器添加Shell CGI 支持 前言一、调试环境操作系统:Windows 10 专业版调试环境调试…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
