数据结构复习指导之外部排序
目录
外部排序
复习提示
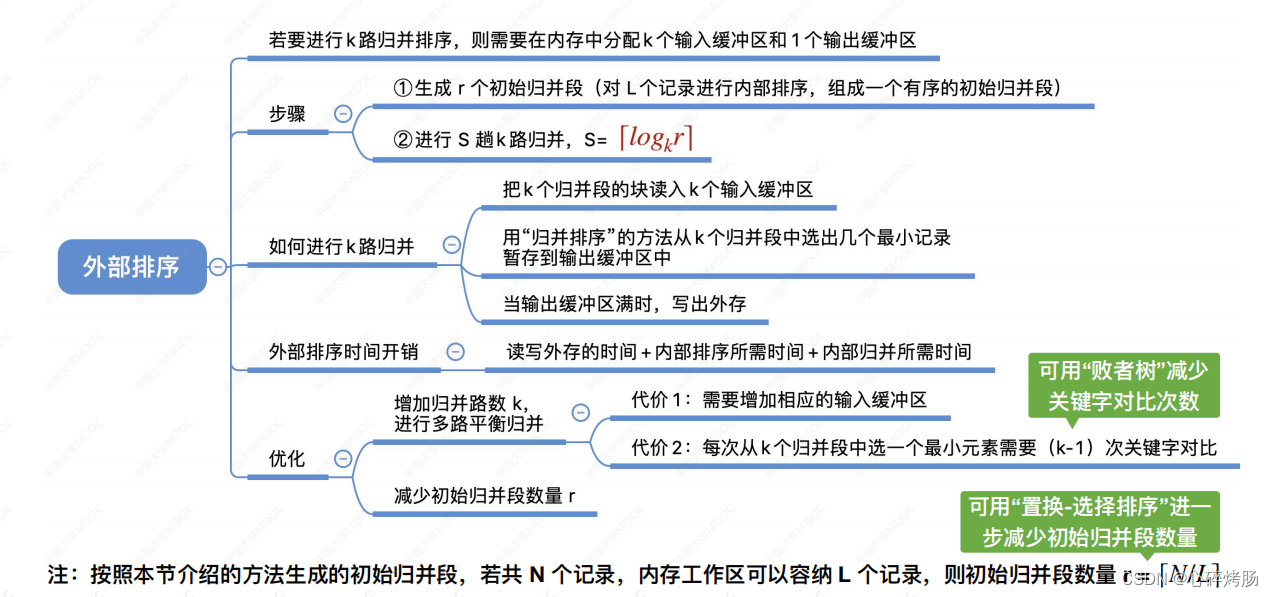
1.外部排序的基本概念
2.外部排序的方法
2.1对大文件排序时使用的排序算法(2016)
3.多路平衡归并与败者树
4.置换-选择排序(生成初始归并段)
4.1置换-选择排序生成初始归并段的实例(2023)
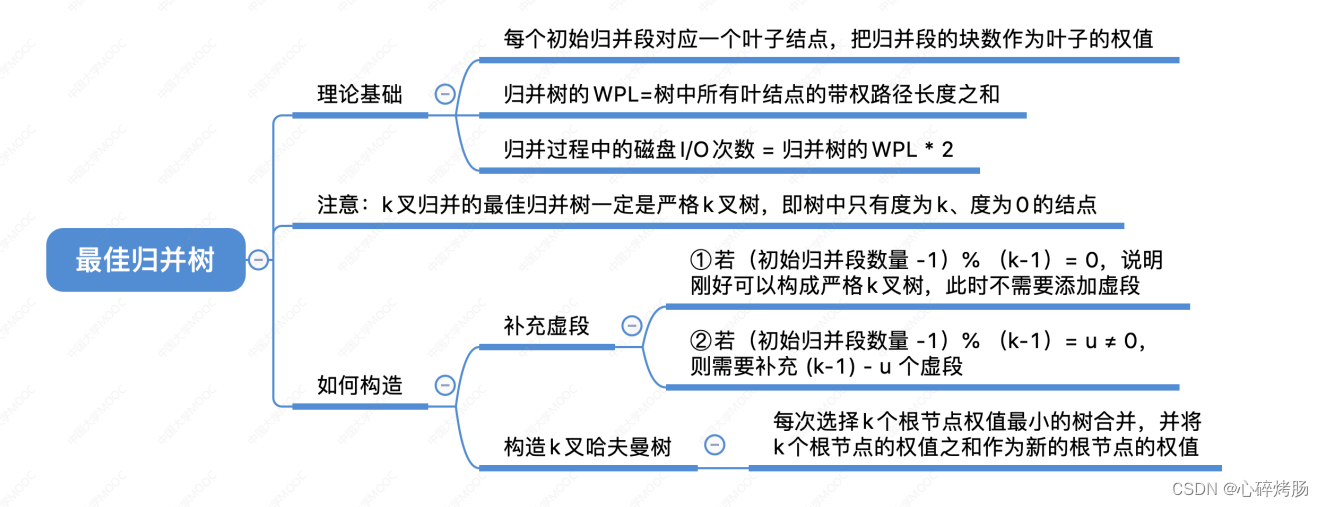
5.最佳归并树
5.1构造三叉哈夫曼树及相关的分析和计算(2013)
5.2实现最佳归并时需补充的虚段数量的分析(2019)
知识回顾
外部排序
复习提示
外部排序可能会考查相关概念、方法和排序过程,外部排序的算法比较复杂,不会在算法设计上进行考查。
本节的主要内容有:
① 外部排序指的是大文件的排序,即待排序的记录存储在外存中,待排序的文件无法一次性装入内存,需要在内存和外存之间进行多次数据交换,以达到排序整个文件的目的。
② 为减少平衡归并中外存读/写次数所采取的方法:增大归并路数和减少归并段个数。
③ 利用败者树增大归并路数。
④ 利用置换-选择排序增大归并段长度来减少归并段个数。
⑤ 由长度不等的归并段进行多路平衡归并,需要构造最佳归并树。
1.外部排序的基本概念
前面介绍过的排序算法都是在内存中进行的(称为内部排序)。
而在许多应用中,经常需要对大文件进行排序,因为文件中的记录很多,无法将整个文件复制进内存中进行排序。
因此,需要将待排序的记录存储在外存上,排序时再把数据一部分一部分地调入内存进行排序,在排序过程中需要多次进行内存和外存之间的交换。
这种排序算法就称为外部排序。
2.外部排序的方法
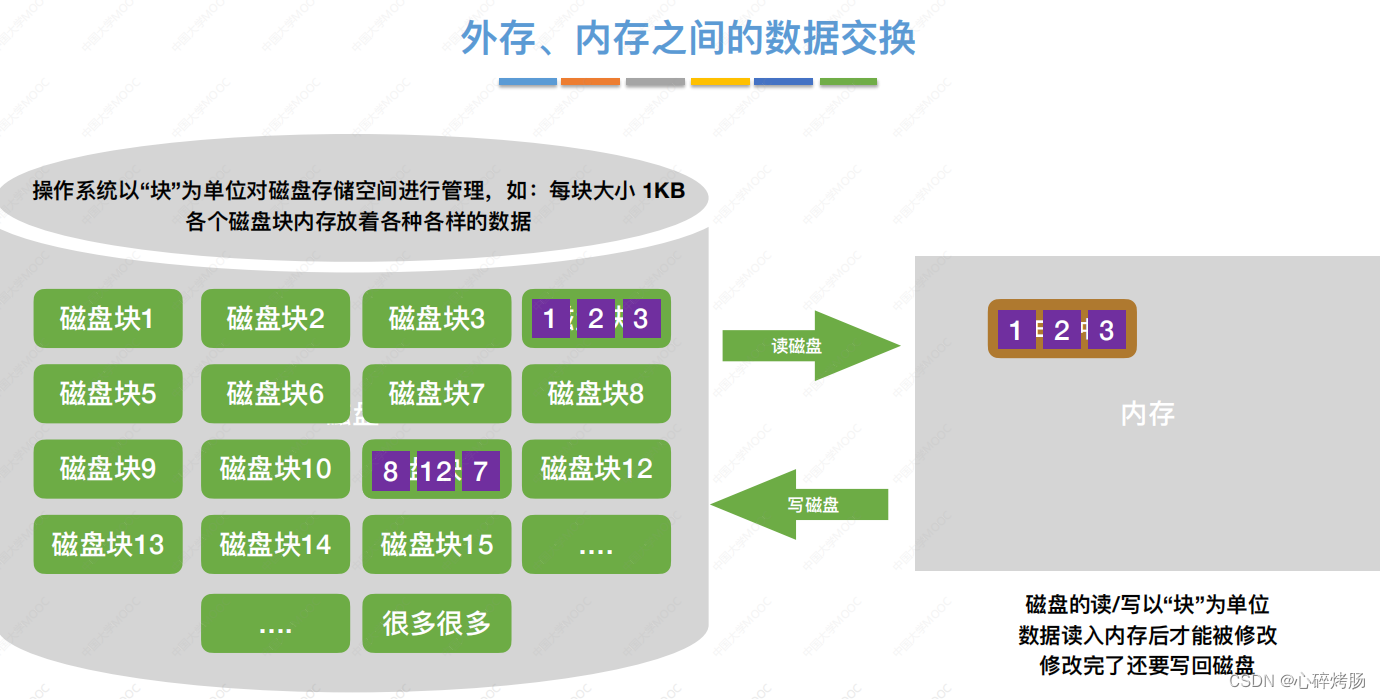
文件通常是按块存储在磁盘上的,操作系统也是按块对磁盘上的信息进行读/写的。
因为磁盘读/写的机械动作所需的时间远远超过在内存中进行运算的时间(相比而言可以忽略不计),
因此在外部排序过程中的时间代价主要考虑访问磁盘的次数,即I/O次数。
2.1对大文件排序时使用的排序算法(2016)
外部排序通常采用归并排序算法。它包括两个阶段:
- ① 根据内存缓冲区大小,将外存上的文件分成若干长度为 L 的子文件,依次读入内存并利用内部排序算法对它们进行排序,并将排序后得到的有序子文件重新写回外存,称这些有序子文件为归并段或顺串;
- ② 对这些归并段进行逐趟归并,使归并段(有序子文件)逐渐由小到大,直至得到整个有序文件为止。
例如,一个含有 2000个记录的文件,每个磁盘块可容纳 125 个记录,首先通过8次内部排序得到 8个初始归并段 R1~R8,每段都含 250 条记录。
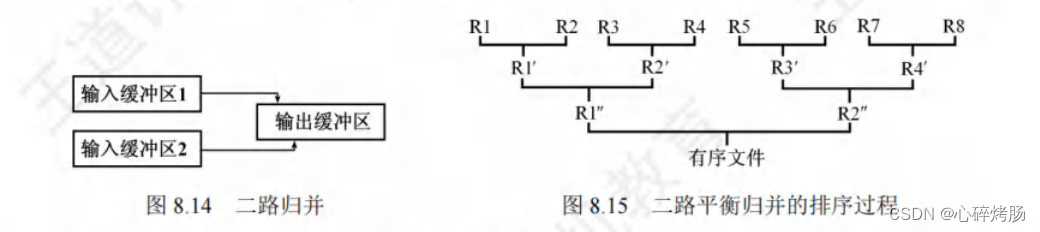
然后对该文件做如图 8.15 所示的两两归并,直至得到一个有序文件。
可以把内存工作区等分为三个缓冲区,如图8.14所示,其中的两个为输入缓冲区,一个为输出缓冲区。
首先,从两个输入归并段R1和 R2 中分别读入一个块,放在输入缓冲区1和输入缓冲区2中。
然后,在内存中进行二路归并,归并后的对象顺序存放在输出缓冲区中。
若输出缓冲区中对象存满,则将其顺序写到输出归并段(R1')中,再清空输出缓冲区,继续存放归并后的对象。
若某个输入缓冲区中的对象取空,则从对应的输入归并段中再读取下一块,继续参加归并。
如此继续,直到两个输入归并段中的对象全部读入内存并都归并完成为止。
当 R1 和 R2 归并完后,再归并 R3 和 R4、R5 和 R6、最后归并 R7和 R8,这是一趟归并。
再把上趟的结果 R1'和 R2'、R3'和 R4'两两归并,这又是一趟归并。
最后把 R1"和 R2"两个归并段归并,得到最终的有序文件,一共进行了3趟归并。
在外部排序中实现两两归并时,由于不可能将两个有序段及归并结果段同时存放在内存中,因此需要不停地将数据读出、写入磁盘,而这会耗费大量的时间。
一般情况下:
外部排序的总时间 = 内部排序的时间 + 外存信息读/写的时间 + 内部归并的时间
显然,外存信息读/写的时间远大于内部排序和内部归并的时间,因此应着力减少 I/O 次数。
由于外存信息的读/写是以“磁盘块”为单位的,因此可知每趟归并需进行 16 次读和 16 次写,3趟归并加上内部排序时所需进行的读/写,使得总共需进行 32x3 +32=128 次读/写。
若改用 4 路归并排序,则只需2趟归并,外部排序时的总读/写次数便减至 32x2+32=96。
因此,增大归并路数,可减少归并趟数,进而减少总的磁盘 I/O 次数,如图 8.16 所示。

一般地,对 r 个初始归并段,做 k 路平衡归并(即每趟将 k 个或 k 个以下的有序子文件归并成一个有序子文件)。
第一趟可将 r 个初始归并段归并为个归并段,以后每趟归并将 m 个归并段归并成
个归并段,直至最后形成一个大的归并段为止。
树的高度-1=
= 归并趟数S。
可见,只要增大归并路数k,或减少初始归并段个数r,都能减少归并趟数 S,进而减少读/写磁盘的次数,达到提高外部排序速度的目的。

3.多路平衡归并与败者树
增加归并路数 k 能减少归并趟数 S,进而减少 I/O 次数。
然而,增加归并路数 k 时,内部归并的时间将增加。
做内部归并时,在 k 个元素中选择关键字最小的元素需要k-1次比较。
每趟归并 n 个元素需要做 (n-1)(k-1) 次比较,S趟归并总共需要的比较次数为
式中,随 k 增长而增长,因此内部归并时间亦随 k 的增长而增长。
这将抵消因增大 k 而减少外存访问次数所得到的效益。因此,不能使用普通的内部归并排序算法。
为了使内部归并不受 k 的增大的影响,引入了败者树。
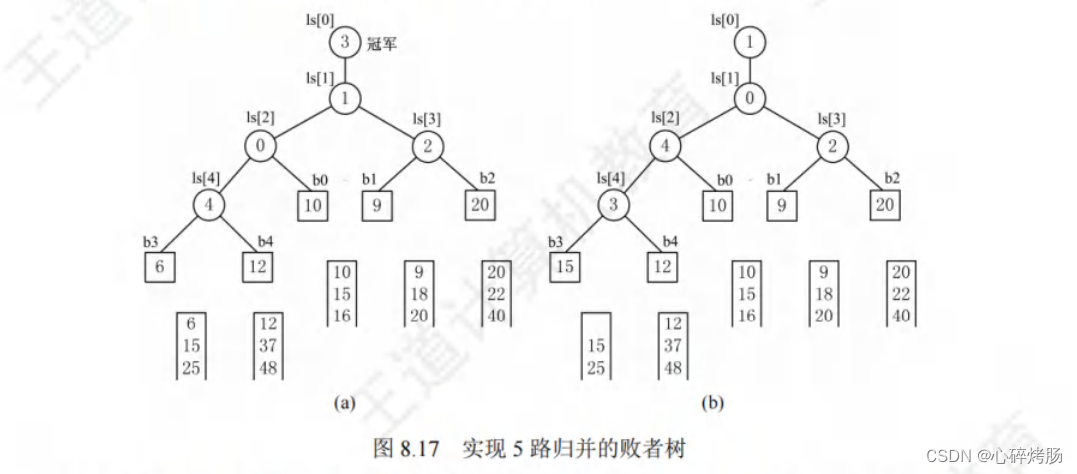
败者树是树形选择排序的一种变体,可视为一棵完全二叉树。
k 个叶结点分别存放 k 个归并段在归并过程中当前参加比较的元素,内部结点用来记忆左右子树中的“失败者”,而让胜利者往上继续进行比较,一直到根结点。
若比较两个数,大的为失败者、小的为胜利者,则根结点指向的数为最小数。
如图 8.17(a) 所示,
- b3 与 b4 比较,b4 是败者,将段号 4 写入父结点 ls[4](l为小写的L,并非大写的i,下面同理)。
- b1 与 b2 比较,b2 是败者,将段号 2 写入 ls[3]。
- b3 与 b4的胜者 b3 与 b0 比较,b0 是败者,,将段号0写入 Is[2]。
- 最后两个胜者 b3 与 b1 比较,b1是败者,将段号1写入Is[1]。
- 而将胜者b3 的段号3写入 ls[0] 此时,根结点 Is[0] 所指的段的关键字最小。
对于k路归并,初始构造败者树需要k-1次比较。
b3 中的 6 输出后,将下一关键字填入 b3,继续比较。
因为 k 路归并的败者树深度为,所以从 k 个记录中选择最小关键字,仅需进行
次比较。
因此总的比较次数约为
可见,使用败者树后,内部归并的比较次数与 k 无关了。
因此,只要内存空间允许,增大归并路数 k 将有效地减少归并树的高度,从而减少 I/O 次数,提高外部排序的速度。
值得说明的是,归并路数 k 并不是越大越好。
归并路数 k 增大时,相应地需要增加输入缓冲区的个数。
若可供使用的内存空间不变,势必要减少每个输入缓冲区的容量,使得内存、外存交换数据的次数增大。
当k值过大时,虽然归并趟数会减少,但读/写外存的次数仍会增加。
4.置换-选择排序(生成初始归并段)
从 《外部排序的方法》节的讨论可知,减少初始归并段个数,也可以减少归并趟数 S。
若总的记录个数为n,每个归并段的长度为 l(此l为小写的L,并非大写的i),则归并段的个数。
采用内部排序算法得到的各个初始归并段长度都相同(除最后一段外),它依赖于内部排序时可用内存工作区的大小。
因此,必须探索新的方法,用来产生更长的初始归并段,这就是本节要介绍的置换-选择算法。
4.1置换-选择排序生成初始归并段的实例(2023)
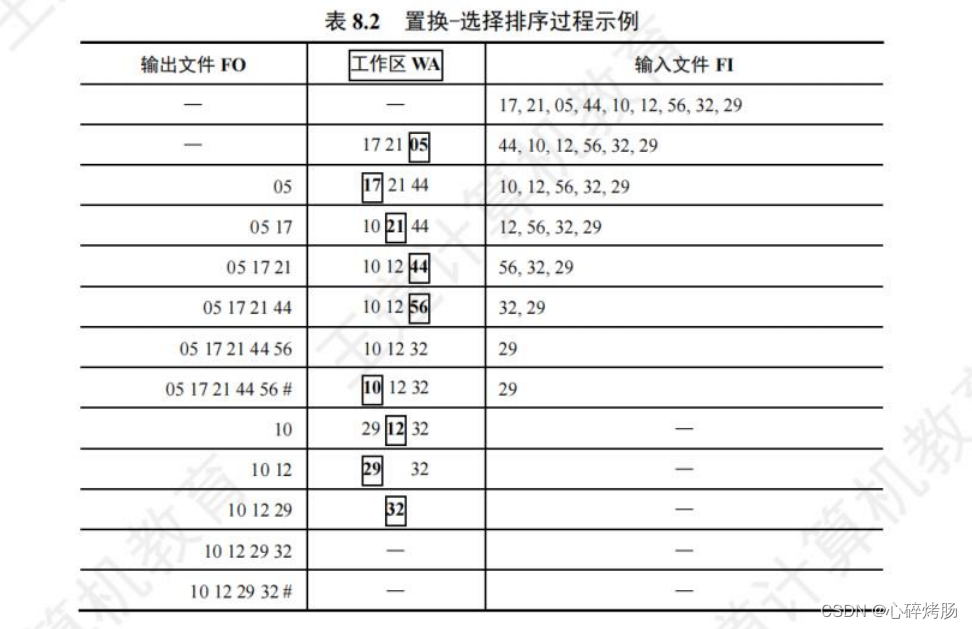
设初始待排文件为FI(此I为大写的i,非小写的L),初始归并段输出文件为FO,内存工作区为 WA,FO 和 WA 的初始状态为空,WA可容纳 w 个记录。
置换-选择算法的步骤如下:
1) 从 FI 输入 w 个记录到工作区 WA。
2) 从 WA 中选出其中关键字取最小值的记录,记为 MINIMAX 记录。
3) 将 MINIMAX 记录输出到 FO 中去。
4) 若 FI 不空,则从 FI 输入下一个记录到 WA 中。
5) 从 WA 中所有关键字比 MINIMAX 记录的关键字大的记录中选出最小关键字记录,作为新的 MINIMAX 记录。
6) 重复 3)~5),直至在 WA 中选不出新的 MINIMAX 记录为止,由此得到一个初始归并段,输出一个归并段的结束标志到FO中去。
7) 重复 2)~6),直至 WA 为空。由此得到全部初始归并段。
设待排文件 FI={17,21,05,44,10,12,56,32,29},WA 容量为3,排序过程如表 8.2 所示。
上述算法,在 WA 中选择 MINIMAX记录的过程需利用败者树来实现。
5.最佳归并树
文件经过置换-选择排序后,得到的是长度不等的初始归并段。
下面讨论如何组织长度不等的初始归并段的归并顺序,使得 I/O 次数最少。
假设由置换-选择排序得到 9个初始归并段,其长度(记录数)依次为9,30,12,18,3,17,2,6,24。
现做 3 路平衡归并,其归并树如图 8.18 所示。
在图 8.18中,各叶结点表示一个初始归并段,上面的权值表示该归并段的长度,叶结点到根的路径长度表示其参加归并的趟数,各非叶结点代表归并成的新归并段,根结点表示最终生成的归并段。
树的带权路径长度 WPL为归并过程中的总读记录数,所以I/O 次数=2xWPL=484。
5.1构造三叉哈夫曼树及相关的分析和计算(2013)
显然,归并方案不同,所得归并树不同,树的带权路径长度(I/O次数)亦不同。
为了优化归并树的 WPL,可以将哈夫曼树的思想推广到 m 又树的情形,在归并树中,让记录数少的初始归并段最先归并,记录数多的初始归并段最晚归并,就可以建立总的 I/O 次数最少的最佳归并树。
上述 9 个初始归并段可构造成一棵如图 8.19 所示的归并树,按此树进行归并,仅需对外存进行446 次读/写,这棵归并树便称为最佳归并树。

图 8.19 中的哈夫曼树是一棵严格 3 叉树,即树中只有度为 3 或 0 的结点。
若只有8个初始归并段,如上例中少了一个长度为 30 的归并段。
若在设计归并方案时,缺额的归并段留在最后,即除最后一次做二路归并外,其他各次归并仍是 3 路归并,此归并方案的 I/O 次数为 386。
显然这不是最佳方案。
正确的做法是:若初始归并段不足以构成一棵严格 k 叉树(也称正则 k 叉树)时,需添加长度为 0的“虚段”,按照哈夫曼树的原则,权为0的叶子应离树根最远。
因此,最佳归并树应如图 8.20 所示,此时的 I/O 次数仅为 326。

如何判定添加虚段的数目?
设度为 0 的结点有个,度为k的结点有
个,归并树的结点总数为n,则有:
(总结点数 = 度为k的结点数 +度为 0 的结点数)
(总结点数 = 所有结点的度数之和+1)
因此,对严格 k 叉树有,由此可得
。
若(n0-1)%(k-1)=0(%为取余运算),则说明这n0个叶结点(初始归并段)正好可以构造 k 叉归并树。此时,内结点有个。
若(n0-1)%(k-1)=u≠0,则说明对于这 n0个叶结点,其中有u个多余,不能包含在 k叉归并树中。
为构造包含所有 n0 个初始归并段的 k 叉归并树,应在原有 个内结点的基础上再增加 1 个内结点。
它在归并树中代替了一个叶结点的位置,被代替的叶结点加上刚才多出的 u 个叶结点,即再加上k-u-1个空归并段,就可以建立归并树。
5.2实现最佳归并时需补充的虚段数量的分析(2019)
以图 8.19 为例,用 8 个归并段构成 3 叉树,(n0-1)%(k-1)=(8-1)%(3-1)=1,说明7个归并段刚好可以构成一棵严格 3叉树(假设把以5为根的树视为一个叶子)。
为此,将叶子5变成一个内结点,再添加 3-1-1=1个空归并段,就可以构成一棵严格3叉树。
知识回顾

相关文章:

数据结构复习指导之外部排序
目录 外部排序 复习提示 1.外部排序的基本概念 2.外部排序的方法 2.1对大文件排序时使用的排序算法(2016) 3.多路平衡归并与败者树 4.置换-选择排序(生成初始归并段) 4.1置换-选择排序生成初始归并段的实例(2023) 5.最佳…...

【Python报错】已解决TypeError: can only concatenate str (not “int“) to str
解决Python报错:TypeError: can only concatenate str (not “int”) to str 在Python中,字符串连接是常见的操作,但如果你尝试将整数(int)与字符串(str)直接连接,会遇到TypeError: …...

Log4j日志级别介绍
Log4j 是一个广泛使用的 Java 日志记录框架,提供了多种日志级别,用于控制日志输出的详细程度。每个日志级别代表一种特定的重要性和紧急程度。 以下是 Log4j 的常见日志级别及其解读: FATAL(致命) 解释:表…...

[MQTT]服务器EMQX搭建SSL/TLS连接过程(wss://)
👉原文阅读 💡章前提示 本文采用8084端口进行连接,是EMQX 默认提供了四个常用的监听器之一,如果需要添加其他类型的监听器,可参考官方文档🔗管理 | EMQX 文档。 本文使用自签名CA,需要提前在L…...
【纯血鸿蒙】——响应式布局如何实现?
前面介绍了自适应布局,但是将窗口尺寸变化较大时,仅仅依靠自适应布局可能出现图片异常放大或页面内容稀疏、留白过多等问题。此时就需要借助响应式布局能力调整页面结构。 响应式布局 响应式布局是指页面内的元素可以根据特定的特征(如窗口…...

深入理解Django Serializer及其在Go语言中的实现20240604
深入理解Django Serializer及其在Go语言中的实现 在现代Web开发中,前后端分离已成为主流架构模式。作为开发者,我们经常需要处理数据的序列化和反序列化,以便在前后端之间传递数据。在Django中,Serializer是一个强大的工具&#…...

电子纸在日化行业的全新应用
电子纸在日化行业的全新应用 项目背景 在一日化龙头企业他们的洗衣粉产线在AGV小车取料到运输到产品包装工序时,因为取料粉车无明显区分标识,但是产品系列有十大类。在未采用晨控电子纸之前现场采用一个转盘分为十个区域,取料工序上方会有一…...

【Redis】Redis的双写问题
在分布式系统中,双写问题通常是指数据在多个存储系统(例如数据库和缓存)中更新时出现的不一致性。这种问题在使用 Redis 作为缓存层时尤为常见。具体来说,当数据在数据库和 Redis 缓存中存在副本时,任何对数据的更新操…...

生气时,你的“心”会发生什么变化?孟德尔随机化分析猛如虎,结果都是套路...
“不生气不生气,气出病来无人替”,不少人遇事常这样宽慰自己。事实上,“气死”真不是危言耸听。越来越多的研究证明了情绪稳定对健康的重要性,那么,当情绪频繁波动时,我们的心血管究竟会发生什么变化&#…...

页面加载性能分析时,有哪些常见的性能瓶颈需要特别注意?
在进行页面加载性能分析时,以下是一些常见的性能瓶颈,需要特别注意: 长页面加载时间: 页面加载时间超过行业标准或用户期望,导致用户流失。 高 CPU 使用率: 某些脚本或操作导致 CPU 使用率飙升,…...

Scanner
Java 有一个 Scanner 类,用这个类可以接受键盘输入。 步骤: 导入该类所在的包(要使用一个类的话就必须先导入该类所在的包)创建该类的对象调用里面的功能 Scanner 有两套系统。 第一套系统: nextInt(); nextDoubl…...

vue3实现录音与录像上传功能
录音 <script setup lang"ts"> import { onMounted, reactive, ref } from vue; import useInject from /utils/useInject;const props: any defineProps<{params?: any; }>();const recObj: any reactive({blob: null, });const { $global, $fn } …...

PHP小方法
一、随机生成姓名 二、随机获取身份证 三、随机获取手机号 四、随机获取省 五、通过身份证获取生日和性别 六、通过身份证获取年龄 七、获取访问IP 八、获取访问URL地址 九、陆续增加 //一、随机生成姓名 function generateName(){$arrXing getXingList();$numbXing …...
gulimall-search P125 springboot整合elasticsearch版本冲突
一、问题 spring-boot.version 2.2.4.RELEASE,在gulimall-search pom.xml中添加elasticsearch.version 7.4.2后,发现出现如下问题:elasticsearch版本是springboot引入的6.8.6,没有变为7.4.2。 二、原因 在gulimall-search 的pom文件中&#…...

如何在Coze中实现Bot对工作流的精准调用(如何提高Coze工作流调用的准确性和成功率)
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 工作流(workflow)📒📝 创建设计工作流📝 添加工作流📝 调用工作流⚓️ 相关链接 ⚓️📖 介绍 📖 在使用Coze平台创建智能Bot时,您可能会遇到一个常见问题:即便添加了正确的工作流,Bot却没有按照预期调用它们。…...
毫米波雷达阵列天线设计综合1(MATLAB仿真)
1 天线设计目标 毫米波雷达探测目标的距离、速度和角度,其中距离和角度和天线设计相关性较强。天线增益越高,则根据雷达方程可知探测距离越远;天线波束越窄,则角度分辨率越高;天线副瓣/旁瓣越低,则干扰越少…...

Freemarker
Freemarker简介 Freemarker是一个用Java语言编写的模板引擎,用于基于模板和数据生成文本输出。它可以用于生成HTML网页、XML文档、电子邮件、配置文件等任何格式的文本。Freemarker将业务逻辑与表示逻辑分离,使得开发人员可以专注于功能实现,…...

基于Zero-shot实现LLM信息抽取
基于Zero-shot方式实现LLM信息抽取 在当今这个信息爆炸的时代,从海量的文本数据中高效地抽取关键信息显得尤为重要。随着自然语言处理(NLP)技术的不断进步,信息抽取任务也迎来了新的突破。近年来,基于Zero-shot&#x…...
【python】tkinter GUI编程经典用法,Label标签组件应用实战详解
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...
国产操作系统上给麒麟虚拟机安装virtualbox增强工具 _ 统信 _ 麒麟 _ 中科方德
原文链接:国产操作系统上给麒麟虚拟机安装virtualbox增强工具 | 统信 | 麒麟 | 中科方德 Hello,大家好啊!昨天给大家带来了一篇在国产操作系统上给VirtualBox中的Win7虚拟机安装增强工具的文章,今天我们将继续深入,介绍…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
