代码随想录算法训练营day41
题目:01背包理论基础、416. 分割等和子集
参考链接:代码随想录
动态规划:01背包理论基础
思路:01背包是所有背包问题的基础,第一次看到比较懵,完全不知道dp数据怎么设置。具体分析还是dp五部曲,首先是dp数据,先想本题需要求的内容,即给定背包容量下,求能放置物品的最大价值和,因此想到的数据存放内容肯定是最大价值和,但本题有容量和物品两个维度,而之前的题目都只有一个维度,故需要用到二维数据,dp[i][j]表示从下标0-i物品中选择任意物品放入容量为j的背包中,能得到的最大价值和;
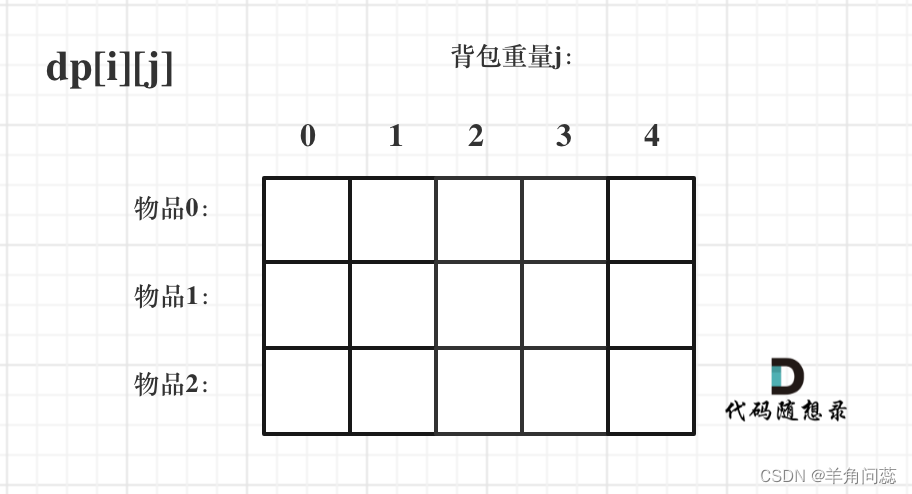
然后第二步递推公式,要递推考虑第i个物品,有两种情况,首先是不放i物品,这时候dp[i][j]=dp[i-1][j],与前i-1个物品的结果相同,然后是放i物品,这时候背包还剩下的重量为j-weight[i],然后在这些重量中放置前i-1个物品,dp[i][j]=dp[i-1][j-weight[i]]+value[i],最终递推即在这两个里取最大值,如果物品i本来就放不进去,那么就只有第一种情况;第三部dp初始化,首先是j=0的时候,背包放不了任何东西,故dp[i][0]=0,然后是i=0即只有物品0的时候,这时候就是看背包能不能放下weight[0],如果放得下则为weight[0],否则为0,其他都被初始化为0;第四步为确定遍历顺序,先遍历物品和背包都可以,因为都是左上推右下,我们就先遍历物品;举例略。时间复杂度O(mn)。
#include<iostream>
#include<cstring>
using namespace std;int maxValue(int n,int m,int space[],int value[]){int dp[m][n+1];//空间需要0-n,物品从0-m-1即可memset(dp,0,sizeof(dp));for(int i=1;i<=n;i++){//初始化物品0if(space[0]<=i){//物品0可以放进背包了dp[0][i]=value[0];}}for(int i=1;i<m;i++){for(int j=1;j<=n;j++){if(space[i]>j){//物品i无法先放进去dp[i][j]=dp[i-1][j];}else{//先放物品idp[i][j]=max(dp[i-1][j],dp[i-1][j-space[i]]+value[i]);}}}return dp[m-1][n];
}int main(){int n,m;while(cin >> m >> n){int space[m],value[m];for(int i=0;i<m;i++){cin >> space[i];}for(int i=0;i<m;i++){cin >> value[i];}cout << maxValue(n,m,space,value) << endl;}return 0;
}
我比较喜欢的ACM写法是把解题过程抽象成一个函数,数据输入全部在main中完成,标答是在solve()中处理输入。
看标答发现可以把数据压缩成一维,因为递推公式的i都是i-1,我们可以只保留每一行,也就是滚动数组。新的一维dp数组dp[j]表示容量为j的背包能装入的最大价值;递归公式,还是看物品i能不能先放进去,如果不能,那么dp[j]就不变,如果能放先放进去,那么就比较当前dp[j]和dp[j-weight[i]]+value[i],取最大值;初始化,只初始化一行,dp[0]肯定为0,其他下标位置,也初始化为0,因为后面递推过程中会逐渐取最大值;遍历顺序,这是一维写法比较困难的地方,必须从背包容量从大到小遍历,因为如果从小到大,会把前面的背包放入两次,比如w[0]=1,v[0]=15,在计算dp[1]的过程中即为dp[0]+v[0]=15,而对dp[2],如果取dp[1]+value[0]=30,会算两次物品0,而从大到小遍历,我们一开始没有放入物品,dp[0]初始化均为0,dp[2]=dp[1]+value[0]=15,因为在这一次遍历中,还没有考虑到dp[1],后续计算dp[1]=dp[0]+value[0]=15,故不会重复放入,而之前的二维数组,每一次dp[i][j]都由上一层计算而来,本层的没有被覆盖过,因此不存在重复计算问题;举例略。主要就是为了避免本层覆盖的问题,因为dp数组都是由上一层计算的。一维滚动数组写法的代码如下:
int maxValue(int n,int m,int space[],int value[]){int dp[n+1]={0};for(int i=1;i<=n;i++){//初始化if(space[0]<=i){//物品0可以放进背包了dp[i]=value[0];}}for(int i=1;i<m;i++){for(int j=n;j>=0;j--){if(space[i]<=j){//物品i能先放进去dp[j]=max(dp[j],dp[j-space[i]]+value[i]);}}}return dp[n];
}
真正理解需要画图分析。一维写法空间复杂度大幅下降,需要掌握。
416. 分割等和子集
思路:本题的第一想法就是使用回溯暴力搜索和为sum/2的所有元素,如果找到返回true。能不能套用01背包问题呢,把数组中所有元素对应为物品,每个物品只能放入一次,背包的容量为sum/2,放入的物品重量为元素的数值,价值也为元素的数值,需要保证背包正好装满。对应dp五部曲,首先是dp数组,dp[j]表示背包容量为j时,能放入最大价值,若背包容量为target,则dp[target]即背包装满后的容量,dp[target]=target即装满,如果装不满,即价值未达到要求,dp[target]<target;递推公式,物品i能放进去的时候,dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]),因为物品i的weight和value都是nums[i];初始化,由于题目的价值都是非负,dp直接全初始化为0即可;递推顺序,按重量从大到小;举例略。时间复杂度O(nm),m为和。
class Solution {
public:bool canPartition(vector<int>& nums) {int sum=accumulate(nums.begin(),nums.end(),0);//库函数求和if(sum%2==1){//和为奇数直接排除return false;}int target=sum/2;vector<int> dp(20001,0);//由题意知最大的和不会超过20000int n=nums.size();for(int i=0;i<n;i++){for(int j=target;j>=nums[i];j--){dp[j]=max(dp[j],dp[j-nums[i]]+nums[i]);}}if(dp[target]==target){//容量为target的背包装完后价值恰好为target,即表示装满return true;}return false;}
};
本题的难点就在于将原问题和01背包对应起来,主要是装满如何想到,即把价值和重量都定义成元素的值,装满target重量即为target容量的背包能装的最大价值恰好为target,即dp[target]=target。
相关文章:

代码随想录算法训练营day41
题目:01背包理论基础、416. 分割等和子集 参考链接:代码随想录 动态规划:01背包理论基础 思路:01背包是所有背包问题的基础,第一次看到比较懵,完全不知道dp数据怎么设置。具体分析还是dp五部曲ÿ…...

从0~1开发财务软件
1.获取图形验证码接口 功能要求 1、随机生成6位字符 2、将字符生成base64位格式的图片,返回给前端 3、将生成的字符存储到redis中,用匿名身份id(clientId)作为key,验证码作为value。 clientId通过/login/getClien…...
Python实现连连看9
(2)标识选中的图片 在判断出玩家选中的是哪一张图片之后,接下来就可以标识选中的图片了,即在该选中的图片外围画矩形。代码如下所示。 FIRSTCLICK True #FIRSTCLICK是全局变量 if(click_col>0 and click_row>0) and \(no…...

项目验收总体计划书(实际项目验收原件参考Word)
测试目标:确保项目的需求分析说明书中的所有功能需求都已实现,且能正常运行;确保项目的业务流程符合用户和产品设计要求;确保项目的界面美观、风格一致、易学习、易操作、易理解。 软件全套文档过去进主页。 一、 前言 ࿰…...

C++基础与深度解析 | 异常处理 | 枚举与联合 | 嵌套类与局部类 | 嵌套名字空间与匿名名字空间 | 位域与volatile关键字
文章目录 一、异常处理二、枚举与联合三、嵌套类与局部类四、嵌套名字空间与匿名名字空间五、位域与volatile关键字 一、异常处理 异常处理用于处理程序在调用过程中的非正常行为。 传统的处理方法:传返回值表示函数调用是否正常结束。 例如,返回 0 表示…...

番外篇 | 利用华为2023最新Gold-YOLO中的Gatherand-Distribute对特征融合模块进行改进
前言:Hello大家好,我是小哥谈。论文提出一种改进的信息融合机制Gather-and-Distribute (GD) ,通过全局融合多层特征并将全局信息注入高层,以提高YOLO系列模型的信息融合能力和检测性能。通过引入MAE-style预训练方法,进一步提高模型的准确性。🌈 目录 🚀1.论文解…...

python记录之字符串
在Python中,字符串是一种非常常见且重要的数据类型,用于存储文本信息。下面,我们将对Python字符串进行深入的讲解,包括其基本操作、常见方法、格式化以及高级特性。 1. 字符串的创建 在Python中,字符串可以通过单引号…...
Elasticsearch 认证模拟题 - 15
一、题目 原索引 task1 的字段 title 字段包含单词 The,查询 the 可以查出 1200 篇文档。重建 task1 索引为 task1_new,重建后的索引, title 字段查询 the 单词,不能匹配到任何文档。 PUT task1 {"mappings": {"…...

g++ 预处理 编译 汇编 链接 命令
g 预处理 编译 汇编 链接 命令 在命令行中使用 g 预处理、编译、汇编和链接源代码文件通常遵循以下步骤: 预处理(Preprocessing):将源代码文件转换为经过预处理器处理的中间文件。 g -E source.cpp -o source.i 编译ÿ…...

计算机视觉中的low-level与 high-level任务
文章目录 low-level任务high-level任务区别联系others参考在计算机视觉领域中,low-level任务和high-level任务是两个重要的概念,他们分别涉及图像处理和分析的不同的层次。 low-level任务 low-level任务主要关注的是图像的底层特征,如颜色、纹理、边缘、形状等。通常涉及对…...

安徽京准NTP时钟系统:GPS北斗卫星授时下的生活重塑
安徽京准NTP时钟系统:GPS北斗卫星授时下的生活重塑 安徽京准NTP时钟系统:GPS北斗卫星授时下的生活重塑 时间的流逝自古以来时钟都是人类生活与活动的基础。然而,随着科技的进步,我们对时间管理和测量的方法已经发生了翻天覆地的变…...

图论第8天
685.冗余连接II 这题需要考虑两种情况: 1.两个输入 2.没有两个输入就是有成环 class Solution { public:static const int N 1005;int father[N];int n;void init(){for (int i 0; i < n; i){father[i] i;}}int find(int x){return x father[x] ? x : f…...

Python怎么配置环境变量:深度探索与实战指南
Python怎么配置环境变量:深度探索与实战指南 在Python编程的世界中,环境变量的配置是一个至关重要的步骤。它不仅影响着Python解释器的运行,还关系到各种第三方库和工具的使用。本文将带你深度探索如何配置Python的环境变量,并为…...

计网期末复习指南(六):应用层(DNS、FTP、URL、HTTP、SMTP、POP3)
前言:本系列文章旨在通过TCP/IP协议簇自下而上的梳理大致的知识点,从计算机网络体系结构出发到应用层,每一个协议层通过一篇文章进行总结,本系列正在持续更新中... 计网期末复习指南(一):计算…...

HTML做成一个炫酷跳动爱心的页面
大家好,今天制作制作一个炫酷跳动爱心的页面! 先看具体效果: 要创建一个炫酷跳动爱心的HTML页面,你可以使用HTML、CSS和JavaScript的组合。以下是一个简单的示例,它使用CSS动画和JavaScript来实现跳动效果。 首先&…...
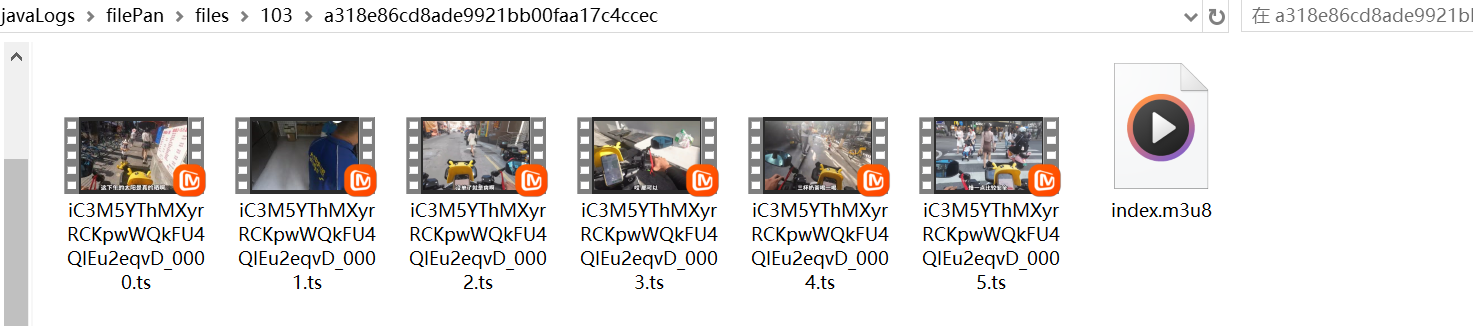
React + SpringBoot实现图片预览和视频在线播放,其中视频实现切片保存和分段播放
图片预览和视频在线播放 需求描述 实现播放视频的需求时,往往是前端直接加载一个mp4文件,这样做法在遇到视频文件较大时,容易造成卡顿,不能及时加载出来。我们可以将视频进行切片,然后分段加载。播放一点加载一点&am…...

Suse Linux ssh配置免密后仍需要输入密码
【问题描述】 Suse Linux已经配置了ssh免密,但无法ssh到目标服务器。 对自身的ssh登陆也需要输入密码。 系统–Suse 15 SP5 【重现步骤】 1.使用ssh-keygen -t rsa生产key文件 2.使用ssh-copy-id拷贝public key到目标机器(或者自身) 3.配置成功后ssh 目标时仍需要输…...
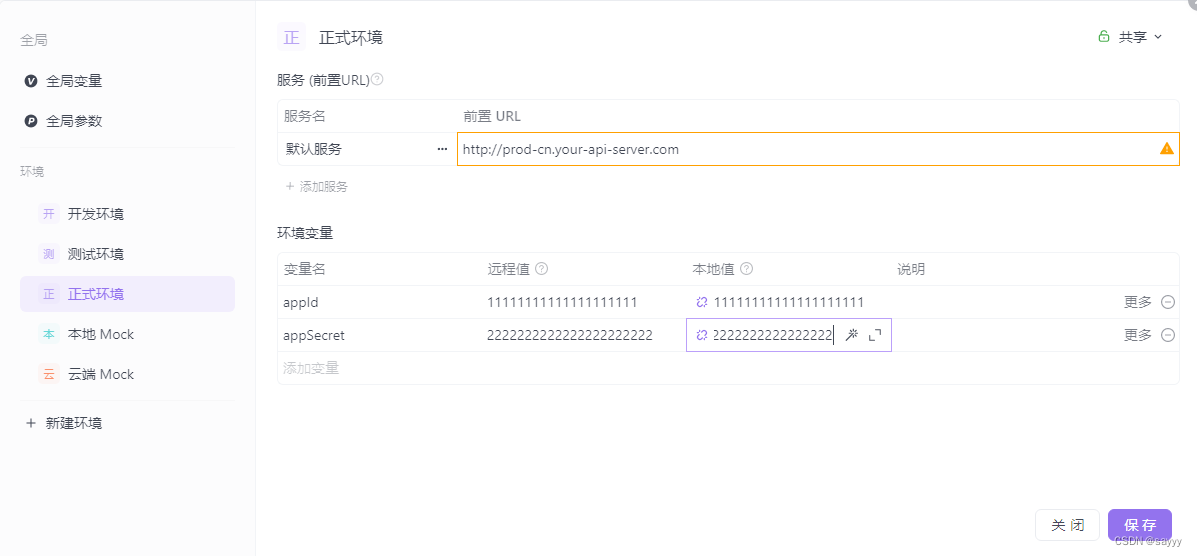
apifox 生成签名
目录 前言准备编写签名脚本签名说明捋清思路编码获取签名所需的参数生成签名将签名放到合适的位置完整代码 在apifox中配置脚本新增公共脚本引用公共脚本添加环境变量 参考 前言 略 准备 查看apifox提供的最佳实践文章:接口签名如何处理 编写签名脚本 签名说明…...

介绍建造者模式
建造者模式 将一个复杂对象的创建与它的表示分离,使得同样的构建过程可以创建不同的表示 四种角色 Product 产品角色 指的是一个具体的产品对象Builder 抽象建造者 创建一个产品对象的各个部件的接口/抽象类ConcreteBuilder 具体建造者 实现或继承抽象建造者接口…...
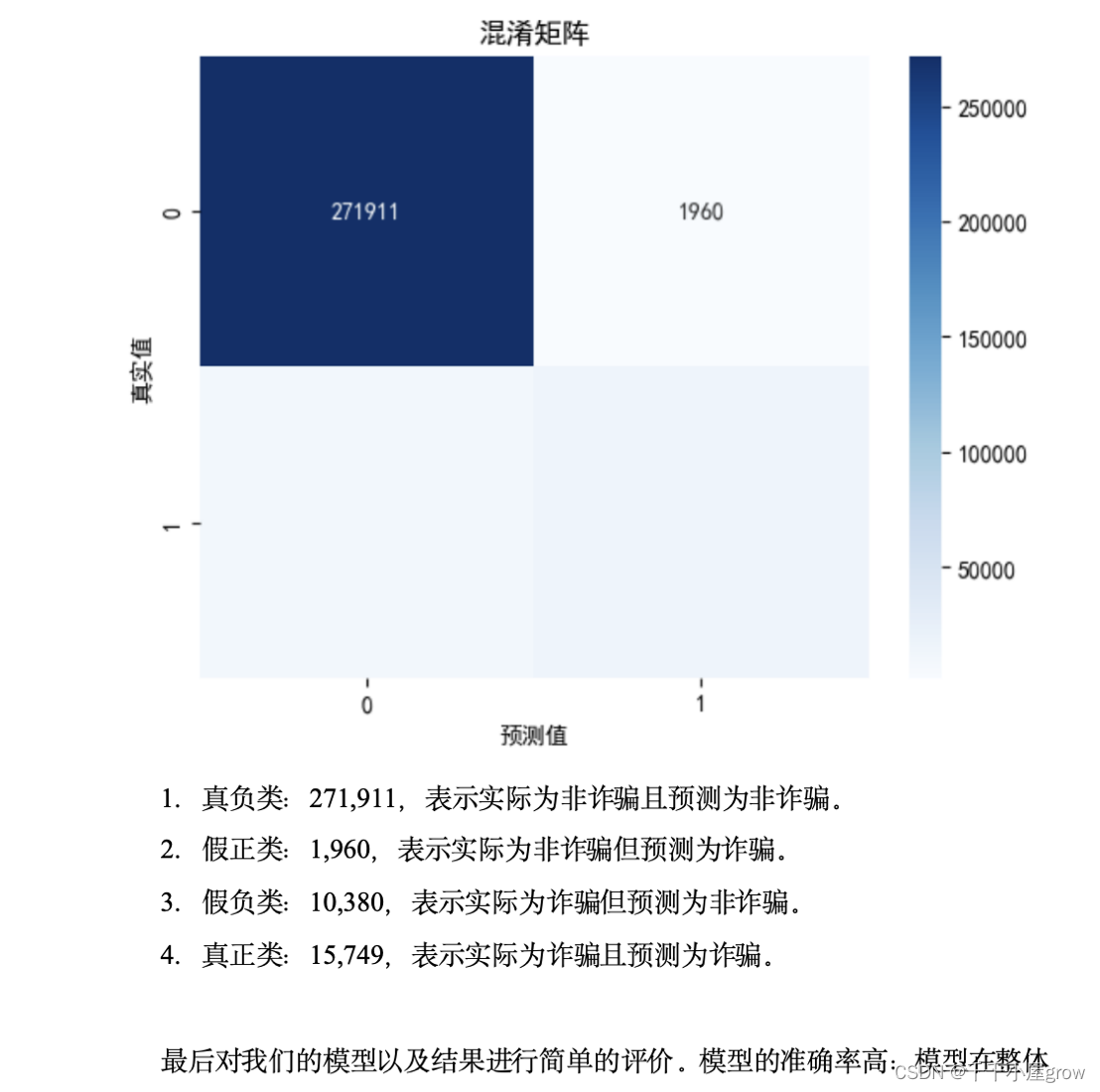
【全部更新完毕】2024全国大学生数据统计与分析竞赛B题思路代码文章教学数学建模-电信银行卡诈骗的数据分析
电信银行卡诈骗的数据分析 摘要 电信银行卡诈骗是当前社会中严重的犯罪问题,分析电信银行卡交易数据,找出高风险交易特征,建立预测模型,将有助于公安部门和金融机构更好地防范诈骗行为,保障用户的财产安全。 针对问…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
