windows系统 flutter 开发环境配置
1、管理员运行powershell,安装:Chocolatey 工具,粘贴复制运行下列脚本:
Chocolatey 官方安装文档
Set-ExecutionPolicy Bypass -Scope Process -Force; [System.Net.ServicePointManager]::SecurityProtocol = [System.Net.ServicePointManager]::SecurityProtocol -bor 3072; iex ((New-Object System.Net.WebClient).DownloadString('https://community.chocolatey.org/install.ps1'))
2、使用choco(Chocolatey 工具) 安装dart-sdk
choco install dart-sdk
3、使用choco安装 fvm (flutter 版本管理工具)
choco install fvm
4、使用fvm 安装 flutter
fvm 命令官方文档
## 查看所有可用的 Flutter SDK 发行版:
fvm releases## 安装对应版本的 flutter
fvm install 3.22.1## 使用 flutter 3.22.1
fvm use 3.22.1## 查看已经使用的flutter版本
fvm flutter --version## 设置flutter 全局版本
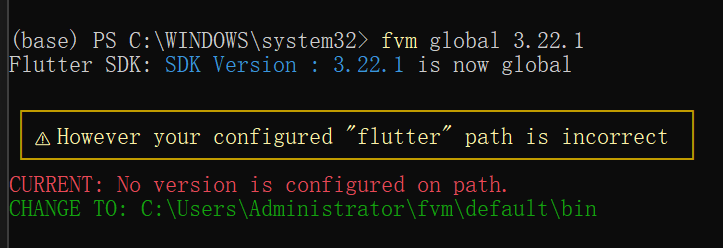
fvm global 3.22.1
##首次设置全局版本,需要配置flutter环境变量,补充见注意部分;
## 查询 flutter版本信息
flutter --version
注意:
首次设置全局版本,需要配置flutter环境变量:
复制 路径,并配置环境变量:
至此,flutter 开发环境配置完成!
相关文章:

windows系统 flutter 开发环境配置
1、管理员运行powershell,安装:Chocolatey 工具,粘贴复制运行下列脚本: Chocolatey 官方安装文档 Set-ExecutionPolicy Bypass -Scope Process -Force; [System.Net.ServicePointManager]::SecurityProtocol [System.Net.ServicePointManage…...
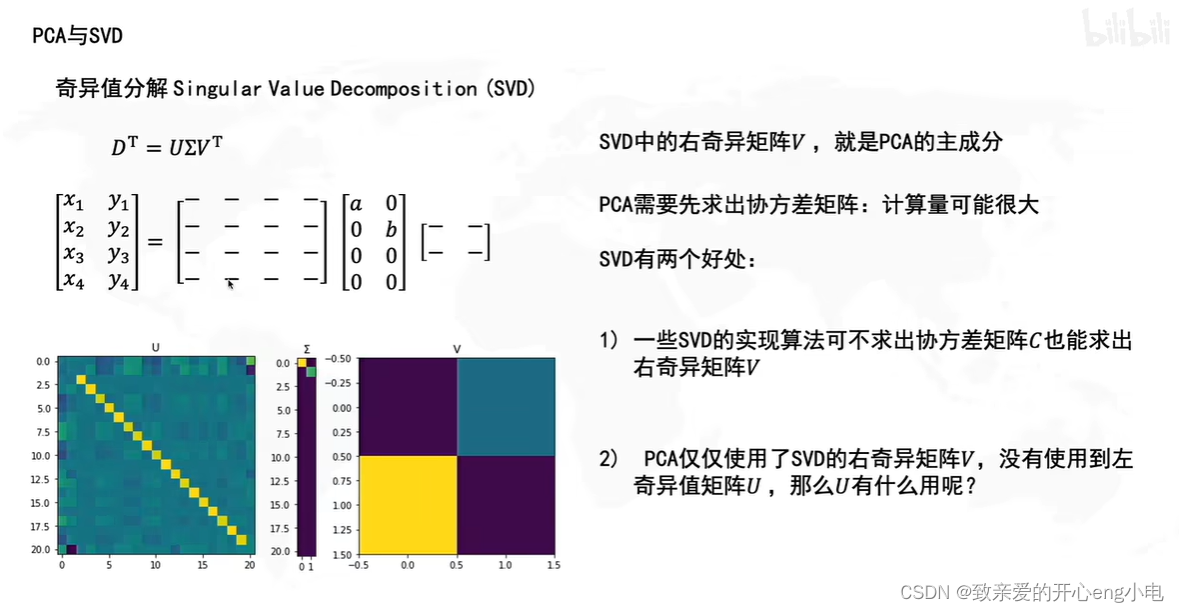
【线性代数】SVDPCA
用最直观的方式告诉你:什么是主成分分析PCA_哔哩哔哩_bilibili 奇异值分解singular value decomposition,SVD principal component analysis,PCA 降维操作 pca就是降维后使得信息损失最小 投影在坐标轴上的点越分散,信息保留越多 pca的实现…...

1.Vue2使用ElementUI-初识及环境搭建
目录 1.下载nodejs v16.x 2.设置淘宝镜像源 3.安装脚手架 4.创建一个项目 5.项目修改 代码地址:source-code: 源码笔记 1.下载nodejs v16.x 下载地址:Node.js — Download Node.js 2.设置淘宝镜像源 npm config set registry https://registry.…...
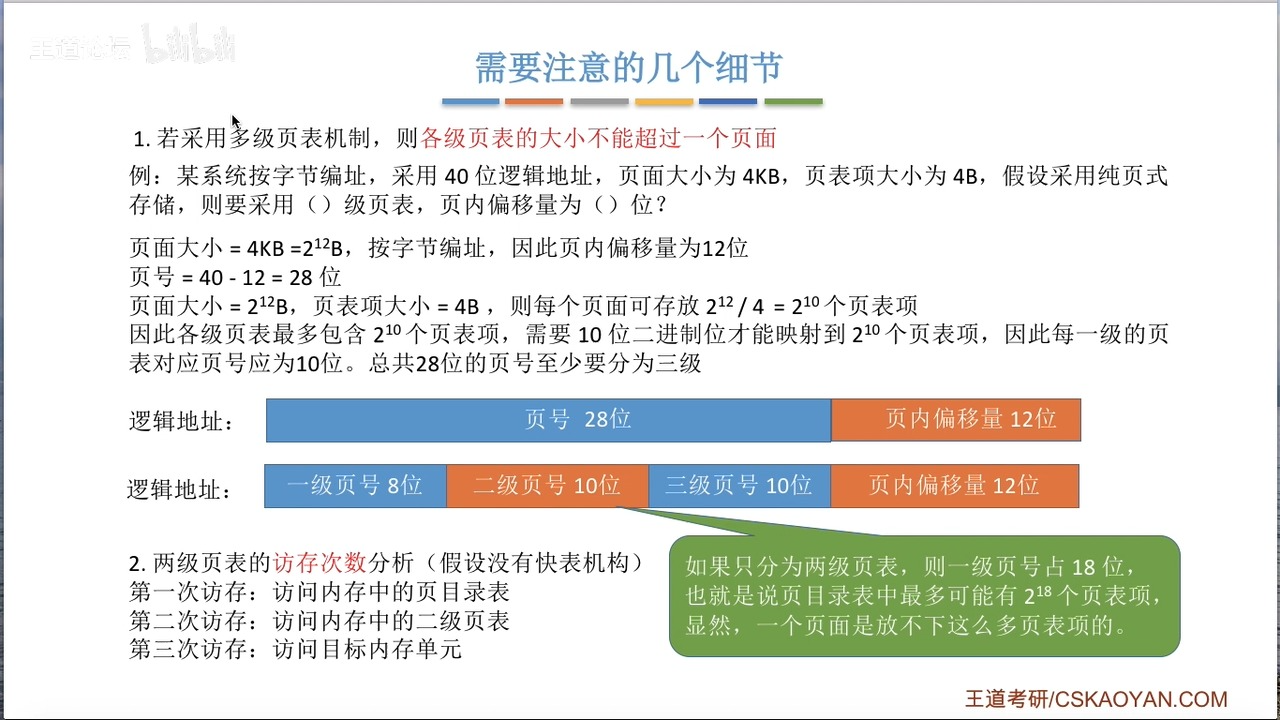
OS复习笔记ch7-3
承接上文我们讲完了页式管理和段式管理,接下来让我们深入讲解一下快表和二级页表 快表 快表和计算机组成原理讲的Cache原理如出一辙。为了减少访存的次数,OS在访问页面的时候创建了快表(Translation Lookaside Buffer ,简称TLB&…...
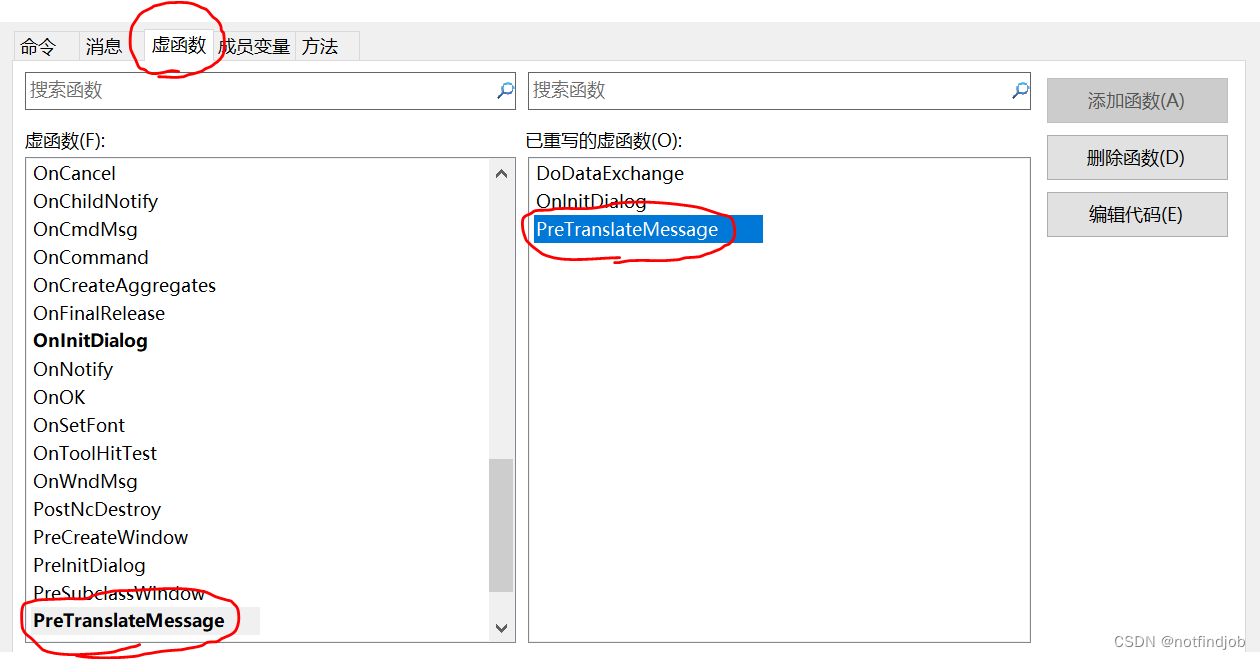
MFC 教程-回车时窗口退出问题
【问题描述】 MFC窗口默认时,按回车窗口会退出 【原因分析】 默认调用OnOK() 【解决办法】 重写虚函PreTranslateMessage BOOL CTESTMFCDlg::PreTranslateMessage(MSG* pMsg) {// TODO: 在此添加专用代码和/或调用基类// 修改回车键的操作反应 if (pMsg->…...
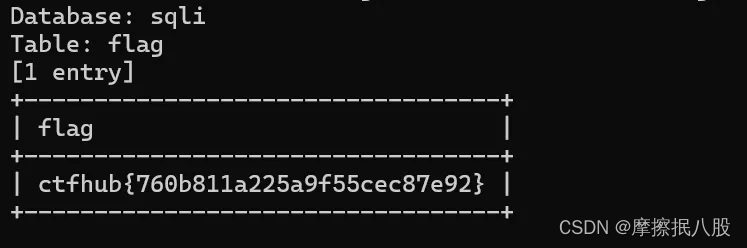
CTFHUB-SQL注入-字符型注入
目录 查询数据库名 查询数据库中的表名 查询表中数据 总结 此题目和上一题相似,一个是整数型注入,一个是字符型注入。字符型注入就是注入字符串参数,判断回显是否存在注入漏洞。因为上一题使用手工注入查看题目 flag ,这里就不…...

Docker配置Redis集群以及主从扩容与缩容
基础镜像拉取 docker run -p 6379:6379 -d redis:6.0.8 配置文件以及数据卷挂载 # 开启密码验证(可选) requirepass 1234 # 允许redis外地连接,需要注释掉绑定的IP # bind 127.0.0.1 # 关闭保护模式(可选) protected-m…...

【计算机网络】 传输层
一、传输层提供的服务 1.1 传输层的功能 1.1.1 传输层的功能如下: 传输层提供应用进程之间的逻辑通信(即端到端的通信)。与网络层的区别是:网络层提供的是主机之间的逻辑通信。 1.1.2 复用和分用 传输层要还要对收到的报文进行…...

山东大学软件学院项目实训-创新实训-基于大模型的旅游平台(二十七)- 微服务(7)
11.1 : 同步调用的问题 11.2 异步通讯的优缺点 11.3 MQ MQ就是事件驱动架构中的Broker 安装MQ docker run \-e RABBITMQ_DEFAULT_USERxxxx \-e RABBITMQ_DEFAULT_PASSxxxxx \--name mq \--hostname mq1 \-p 15672:15672 \-p 5672:5672 \-d \rabbitmq:3-management 浏览器访问1…...

Java Web应用,IPv6问题解决
在Java Web程序中,如果使用Tomcat并遇到了IPv6相关的问题,可以通过以下几种方式来解决: 1. 配置Tomcat以使用IPv4 默认情况下,Java可能会优先使用IPv6。如果你希望Tomcat使用IPv4,最简单的方法是通过设置系统属性来强…...
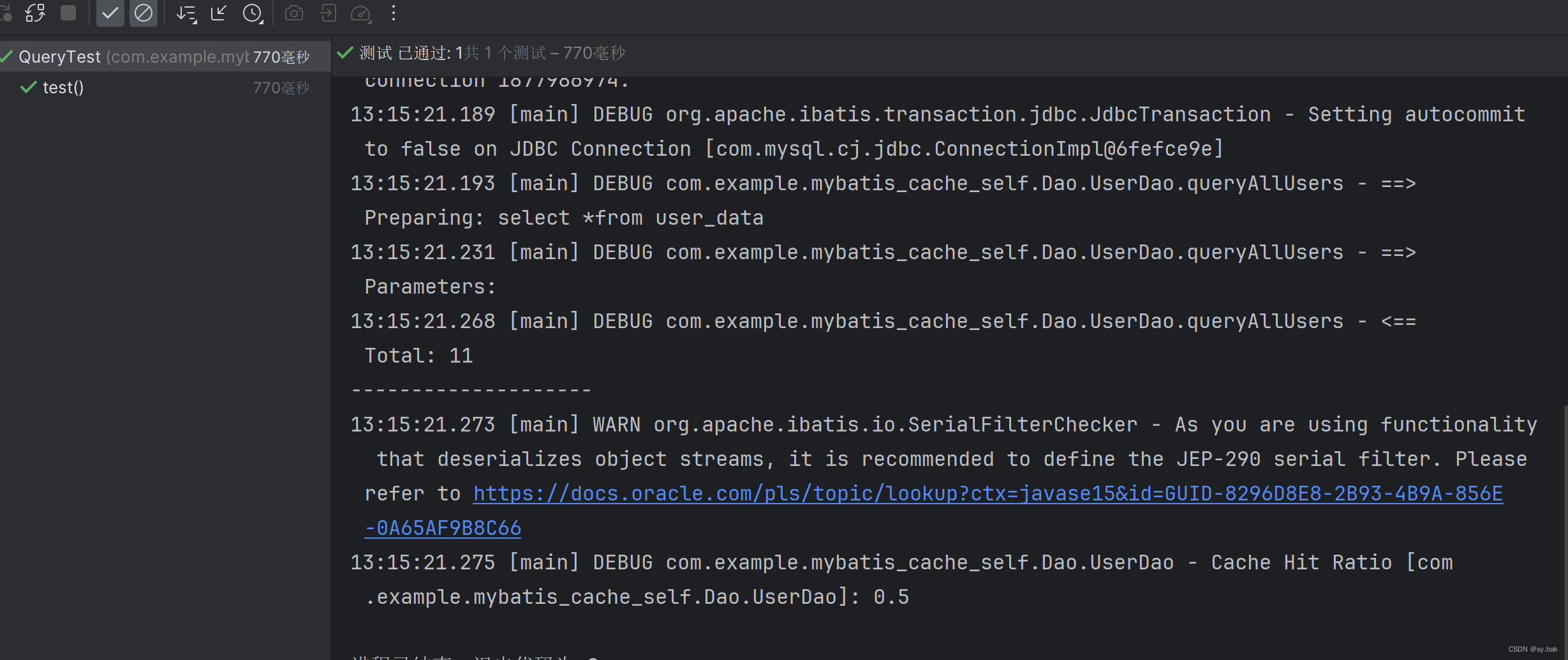
MyBatis二级缓存开启条件
MyBatis缓存为俩层体系。分为一级缓存和二级缓存。 一级缓存: 一级缓存默认开启,一级缓存的作用域是SqlSession级别的,这意味着当你更换SqlSession之后就不能再利用原来的SqlSession的一级缓存了。不同的SqlSession之间的一级缓存是隔离的。…...

golang 不用sleep如何实现实现每隔指定时间执行一次for循环?
今天介绍的是在go语言里面不用time.Sleep, 使用for range 定时器管道 来实现按照我们指定的时间间隔来执行for循环, 即: for range ticker.C { } 这样就实现了for每隔指定时间执行一次,除非管道被关闭,否则for而且会一直柱塞当前线…...

【el-tooltips改造】Vue实现文本溢出才显示el-tooltip,否则不显示el-tooltips
实现原理: 使用disabled属性控制el-tooltip的content显示与隐藏; 目标: 1行省略、多行省略、可缩放页面内的文本省略都有效。 实现方式: 1、自定义全局指令,tooltipAutoShow.js代码如下(参考的el-table中的…...
【Python数据类型的奥秘】:构建程序基石,驾驭信息之海
文章目录 🚀Python数据类型🌈1. 基本概念⭐2. 转化👊3. 数值运算💥4. 数值运算扩展(math库常用函数) 🚀Python数据类型 🌈1. 基本概念 整数(int):整数是没有小数部分的数…...

vue使用html2canvas截图下载时,存在svg或者img或者特殊字体时截图不全的解决办法
使用html2canvas进行div截图时,存在svg和img的解决办法 写在前面:vue使用html2canvas截图时,存在svg或者img或者特殊字体时截图时空白,或者不全解决办法如下第一步,svg或者img先转base64(如果是特殊字体&am…...

机器学习----奥卡姆剃刀定律
奥卡姆剃刀定律(Occam’s Razor)是一条哲学原则,通常表述为“如无必要,勿增实体”(Entities should not be multiplied beyond necessity)或“在其他条件相同的情况下,最简单的解释往往是最好的…...

【设计模式】行为型设计模式之 模板方法模式
介绍 GOF 定义 模板方法模式 Template Method Design Pattern :模板方法模式在一个方法中定义一个算法骨架,并将某些步骤推迟到子类中去实现;模板方法在不改变算法整体结构的情况下,可以重新定义算法中的某些步骤。 代码举例 …...

智能合约中断言失败
断言失败: 断言(assert)在智能合约中用于确保内部逻辑的一致性和正确性,但如果使用不当,确实可能导致意外的合约终止或资金锁定。这是因为assert主要用于检测程序内部的错误,例如算法错误或逻辑错误&#…...

flink读取hive写入http接口
目录 0、创建hive数据 1、pom.xml 2、flink代码 3、sink 4、提交任务jar 5、flink-conf.yaml 6、数据接收 flink-1.17.2jdk1.8hive-3.1.3hadoop3.3.6passwordhttp0、创建hive数据 /cluster/hive/bin/beeline !connect jdbc:hive2://ip:10000 create database demo; d…...
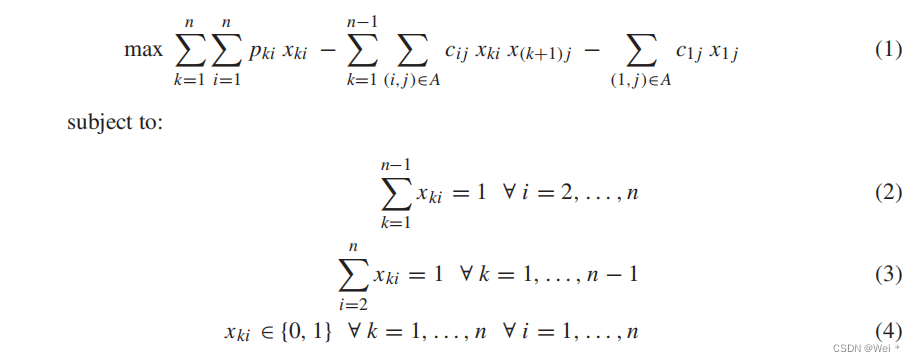
【论文阅读】MODELING AND SOLVING THE TRAVELING SALESMAN PROBLEM WITH PRIORITY PRIZES
文章目录 论文基本信息摘要1.引言2. INTEGER QUADRATIC PROGRAM FOR TSPPP3. MIXED INTEGER LINEAR PROGRAMS FOR TSPPP4. TABU SEARCH ALGORITHM FOR TSPPP5. COMPUTATIONAL RESULTS6. CONCLUDING REMARKS补充 论文基本信息 《MODELING AND SOLVING THE TRAVELING SALESMAN P…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

【Redis】Redis从入门到实战:全面指南
Redis从入门到实战:全面指南 一、Redis简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的键值存储系统,它可以用作数据库、缓存和消息代理。由Salvatore Sanfilippo于2009年开发,因其高性能、丰富的数据结构和广泛的语言支持而广受欢迎。 Redis核心特点:…...