贪心算法-加油站
一、题目描述
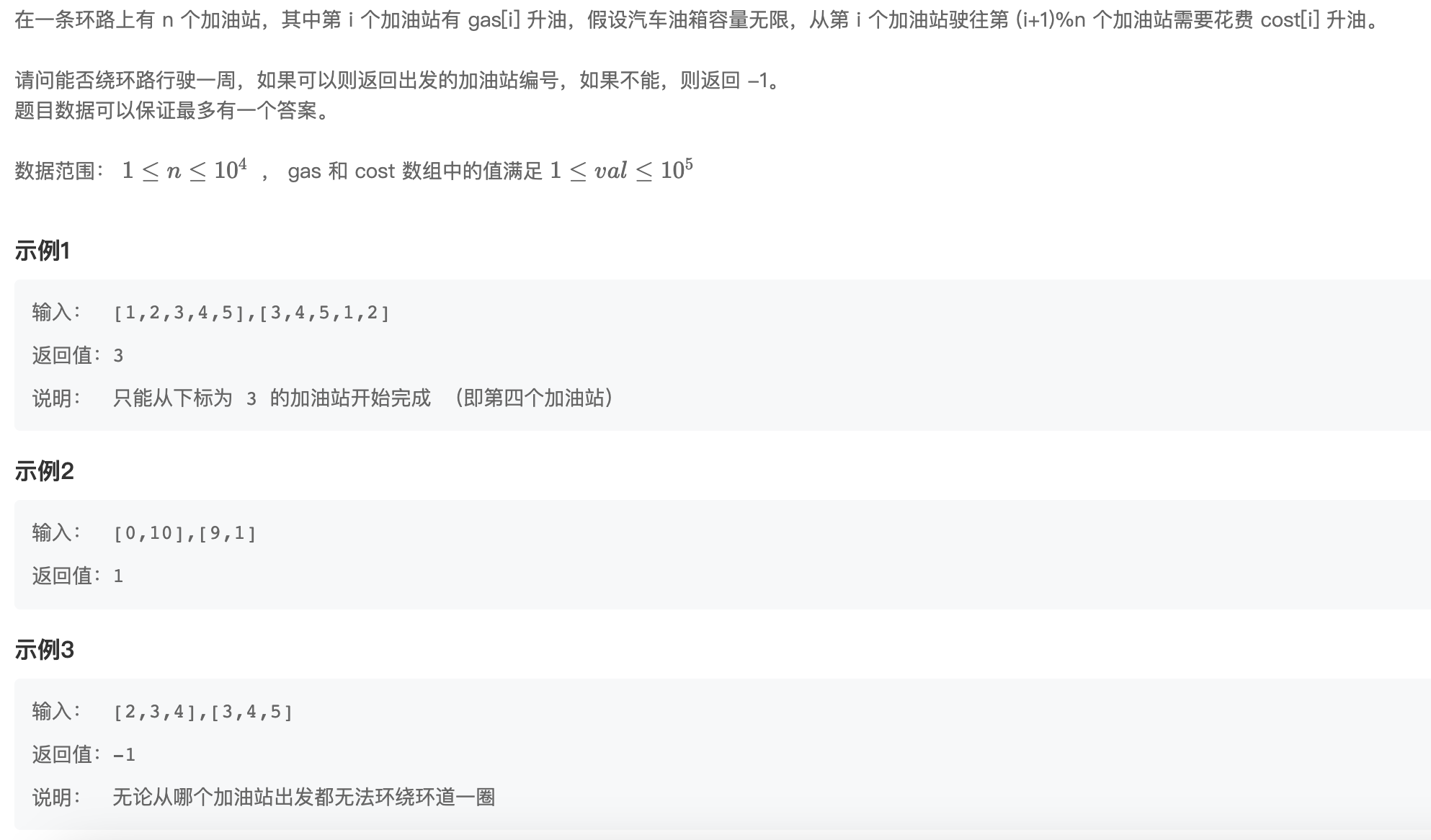
二、解题思路
1.运动过程分析
这里需要一个油箱剩余油量的变量resGas,初始化resGas=0;还需要一个标记从什么位置当做初始位置的startIdx,初始化startIdx=0。
我们从数组下标idx=0处开始向后遍历,初始时startIdx=0,遇到下标为idx的加油站时,看邮箱内此时剩余油量能否到达下一个油站:
resGas=resGas+gas[i]-cost[i]
当resGas>=0时,可以到达下一个油站;
当resGas<0时,不可以到达下一个油站,此时也意味着从startIdx开始运动到达不了idx位置,从startIdx到idx之间的所有位置也同样不可达idx。此时把startIdx设置为idx+1。
这里用startIdx->idx小车运动不可达的图示解释一下上面标注黄色部分:

2.可以循环的条件判断
这里需要注意的是,小车从startIdx->加油站数组末尾时,如果可达,需要将idx=(idx+1)%gas.length,如果整个过程一直可达,等到二次循环idx+1==startidx时,意味着从startIdx开始行驶一定可以循环一周,返回startIdx。所以我们还要添加一个变量标注一下此时是否已经二次循环,实现代码内用newloop来标识。
3.不可以循环的条件判断
不存在循环一周的情况:当二次循环过程中还是出现了不可达的情况,那么就意味着不存在循环的情况,返回-1,图示:
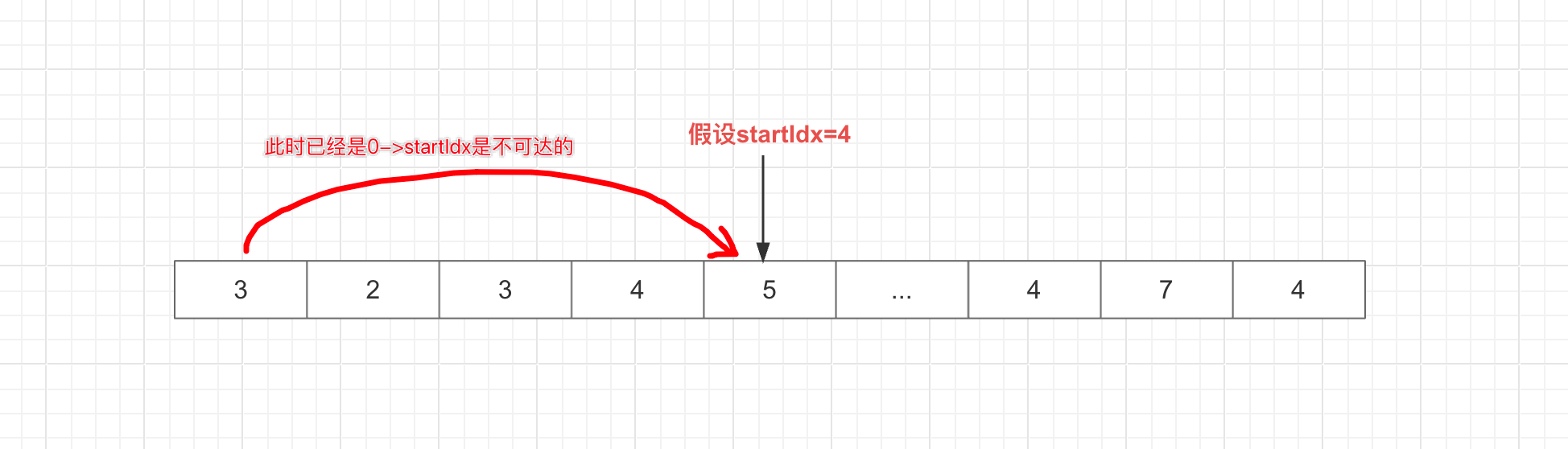

就意味着从startIdx到末尾之间的元素和下标0到下标3之间的所有元素到下标3都不可达,此前已经确定了从下标0到下标4之间的元素已经不可达,所以肯定不能形成循环。
整个过程需要执行两次数组遍历,所以时间复杂度为O(n),效率还是可以的。
三、代码实现
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param gas int整型一维数组 * @param cost int整型一维数组 * @return int整型*/public int gasStation (int[] gas, int[] cost) {// 就从0开始寻找,设置油箱剩余量resGas,int len=gas.length;int startidx=0,residx=0;int resGas=0;//初始时油箱剩余油量为0int nowidx=0;boolean newloop=false;while(nowidx<len){int nowGas=resGas+gas[nowidx]-cost[nowidx];if(nowidx+1==len){newloop=true;}if(nowGas<0){//表示从startidx开始到达不了startidx=(nowidx+1)%len;resGas=0;if(newloop){residx=-1;break;}}else{//表示当前油量还可以支撑往后走resGas=nowGas;if(newloop&&((nowidx+1)%len==startidx)){residx=startidx;break;}}nowidx=(nowidx+1)%len;}return residx;}
}四、刷题链接
加油站_牛客题霸_牛客网
相关文章:

贪心算法-加油站
一、题目描述 二、解题思路 1.运动过程分析 这里需要一个油箱剩余油量的变量resGas,初始化resGas0;还需要一个标记从什么位置当做初始位置的startIdx,初始化startIdx0。 我们从数组下标idx0处开始向后遍历,初始时startIdx0&#…...
)
【ArcGIS微课1000例】0116:将度-分-秒值转换为十进制度值(字段计算器VBA)
相关阅读:【ArcGIS微课1000例】0087:经纬度格式转换(度分秒转度、度转度分秒) 文章目录 一、计算方法二、计算案例一、计算方法 将度分秒转换为十进制度的简单等式: DD = (Seconds/3600) + (Minutes/60) + Degrees如果角度值是负数,则转换方法不同。其中一种方法是: …...
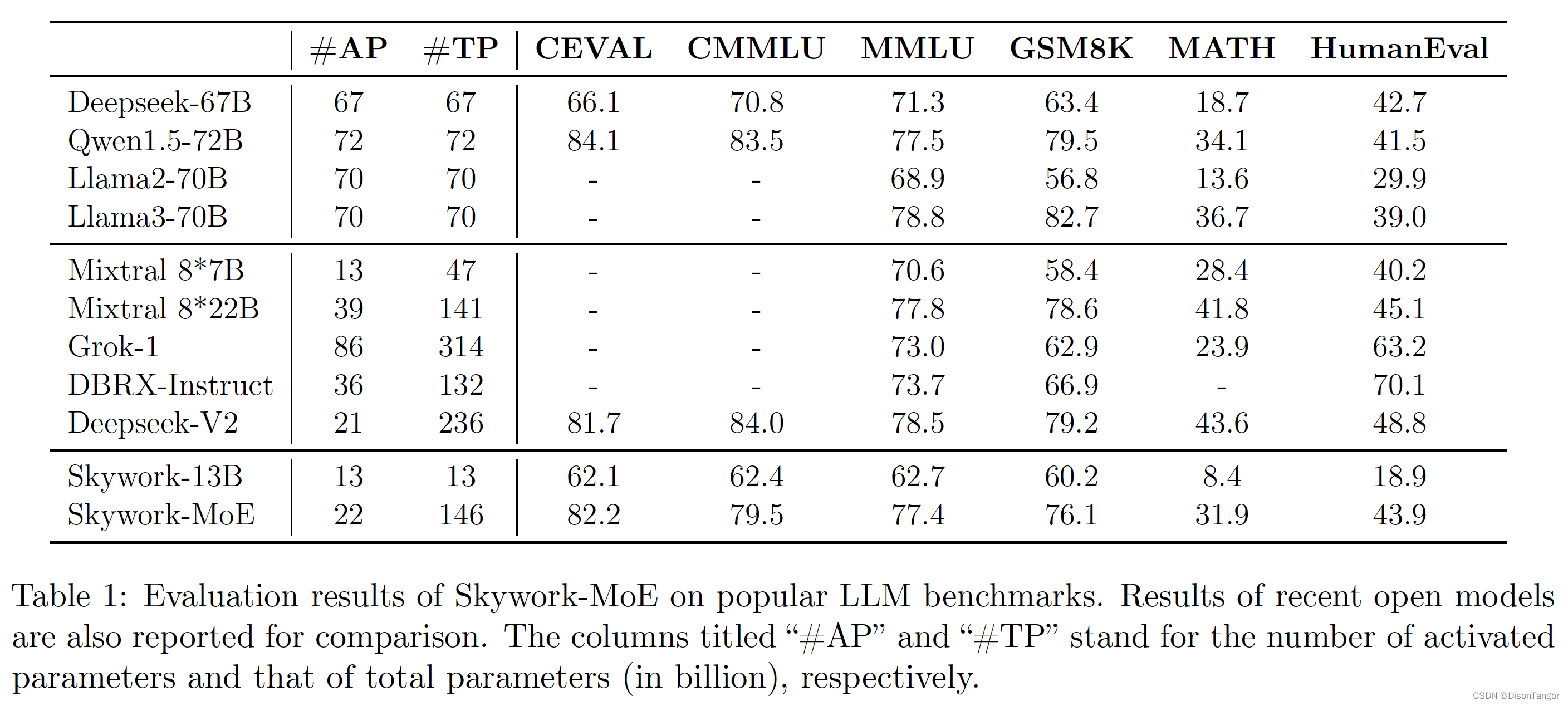
【中国开源生态再添一员】天工AI开源自家的Skywork
刚刚看到《AI高考作文出圈,网友票选天工AI居首》,没想到在Huggingface中发现了Skywork大模型。天工大模型由昆仑万维自研,是国内首个对标ChatGPT的双千亿级大语言模型,天工大模型通过自然语言与用户进行问答式交互,AI生…...
【机器学习300问】109、什么是岭回归模型?
在进行回归任务时间,可以能会遇到特征数量多于观测数量或某些特征变量之间相关性较高(几乎线性相关)时,标准的线性回归模型的系数估计可能非常不精确,可以理解成独立方程个数小于未知数个数此时方程有无穷多解。 例如&…...
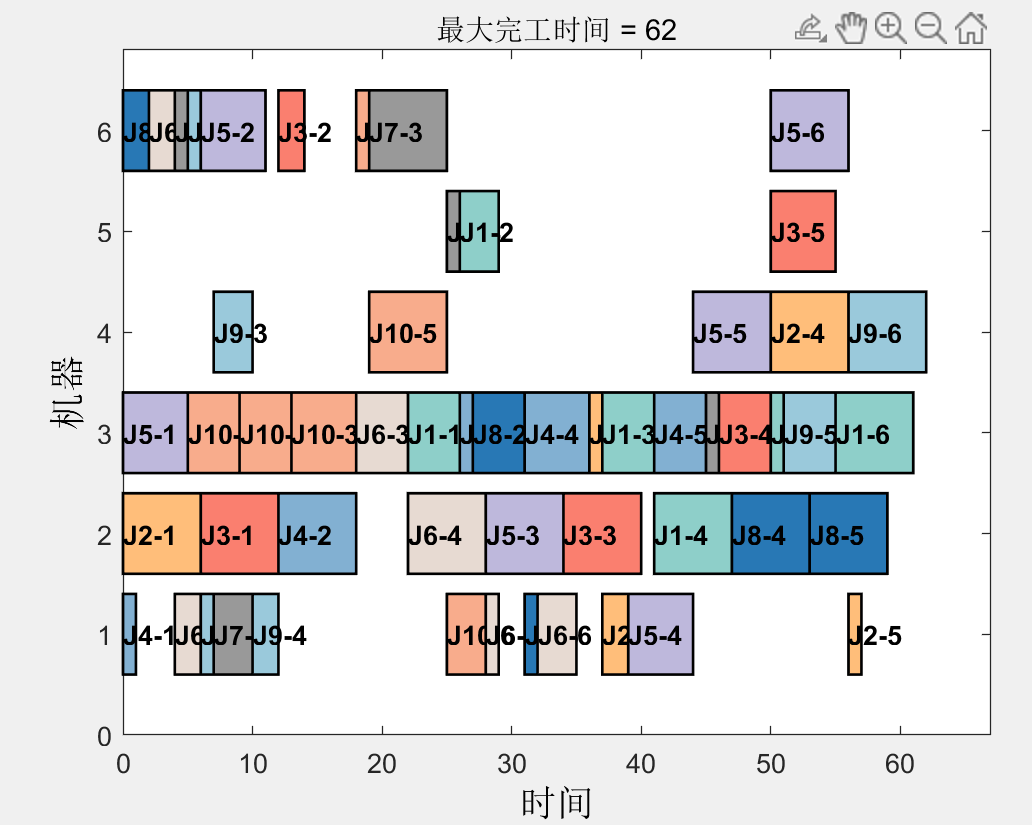
FJSP:烟花算法(FWA)求解柔性作业车间调度问题(FJSP),提供MATLAB代码
一、烟花算法介绍 参考文献: Tan, Y. and Y. Zhu. Fireworks Algorithm for Optimization. in Advances in Swarm Intelligence. 2010. Berlin, Heidelberg: Springer Berlin Heidelberg. 二、烟花算法求解FJSP 2.1FJSP模型介绍 柔性作业车间调度问题(Flexible …...

C++11 列表初始化(initializer_list),pair
1. {} 初始化 C98 中,允许使用 {} 对数组进行初始化。 int arr[3] { 0, 1, 2 };C11 扩大了 {} 初始化 的使用范围,使其可用于所有内置类型和自定义类型。 struct Date {int _year;int _month;int _day;Date(int year, int month, int day):_year(year…...
 和 endswith())
Python3 笔记:字符串的 startswith() 和 endswith()
1、startswith() 方法用于检查字符串是否是以指定子字符串开头,如果是则返回 True,否则返回 False。如果参数 beg 和 end 指定了值,则在指定范围内检查。 语法:str.startswith(substr, beg0,endlen(string)) 参数: s…...

Web前端安全问题分类综合以及XSS、CSRF、SQL注入、DoS/DDoS攻击、会话劫持、点击劫持等详解,增强生产安全意识
前端安全问题是指发生在浏览器、单页面应用、Web页面等前端环境中的各类安全隐患。Web前端作为与用户直接交互的界面,其安全性问题直接关系到用户体验和数据安全。近年来,随着前端技术的快速发展,Web前端安全问题也日益凸显。因此,…...
下列关于脚本的说法不正确的是( )。本题得分: 2分正确答案: A2.单选题 (2分)软件测试自动化的局限性不包含( )。本题得分: 2分)
1.单选题 (2分)下列关于脚本的说法不正确的是( )。本题得分: 2分正确答案: A2.单选题 (2分)软件测试自动化的局限性不包含( )。本题得分: 2分
1.单选题 (2分) 下列关于脚本的说法不正确的是( )。 A 线性脚本是最复杂的脚本 B 结构化脚本具有较好的可读性、可重用性,易于维护 C 关键字驱动脚本在开发时,不关心基础函数,直接使用已定义好的关键字 D 数据驱动脚本将测试脚本和数据进行分离,同一个脚本可以针对不同的输…...

【Docker系列】跨平台 Docker 镜像构建:深入理解`--platform`参数
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

力扣1248.统计优美子数组
力扣1248.统计优美子数组 同930. 哈希表法 求前缀和 class Solution {public:int numberOfSubarrays(vector<int>& nums, int k) {int n nums.size();unordered_map<int,int> cnt;int res0,sum0;for(int i0,j0;i<n;i){cnt[sum] ;if(nums[i] & 1) …...

AI2THOR 2.1.0使用教程
一、安装和入门 1.1 AI2-THOR使用要求 操作系统: Mac OS X 10.9, Ubuntu 14.04显卡:DX9(着色器型号 3.0)或 DX11,功能级别为 9.3。CPU:支持 SSE2 指令集。Python 2.7 或 Python 3.5Linux 用户…...

在Nginx中配置php程序环境。
1、前言。 我一开始是想 搭建 Tomcat PHP 环境。 Tomcat并不能直接运行PHP,因为Tomcat是一个Java Web服务器,主要用于运行Java应用程序。但是,我们可以通过一些配置和工具来使Tomcat能够运行PHP。 在配置Tomcat支持PHP 项目的时…...

!力扣70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 1. 递归(超时) class Solution { public:int climbStairs(int n) {if(n1){return 1;}if(n2){return 2;}return climbStairs…...
Spring boot+vue前后端分离
目录 1、前端vue的搭建 2、后端项目的构建 pom文件中引入的jar包 yml文件用来配置连接数据库和端口的设置 application.property进行一些整合 service层 imp层 mapper 实体类 额外写一个类、解决跨域问题 3、测试 1、前端vue的搭建 建立项目的过程略 开启一个建立好…...

Python基础总结之列表转字符串
Python基础总结之列表转字符串 在Python中,将列表转换为字符串有多种方法,最常用的是使用str.join()方法。这里有一些示例: 使用str.join()方法 这是将列表转换为字符串的最直接和最常用的方法。你需要确保列表中的所有元素都是字符串类型…...

二分【1】二分查找框架 查找指定元素
目录 二分查找 基本思想 几种情况汇总 一。严格递增序列 1.查找本身 2.查找第一个大于等于自己的 3.查找第一个大于自己的 4.严格递减序列 二。有重复元素 1.取其中第一个出现的 2.取其中最后一个出现的 二分查找 基本思想 几种情况汇总 一。严格递增序列 1.查找本身…...

Python 中如何使用 lambda 函数
在 Python 中,可以使用 lambda 函数来创建匿名函数。lambda 函数的语法是:lambda 参数: 表达式。以下是一些使用 lambda 函数的例子: 通过 lambda 函数来计算两个数的和: add lambda x, y: x y print(add(2, 3)) # 输出 5通过…...
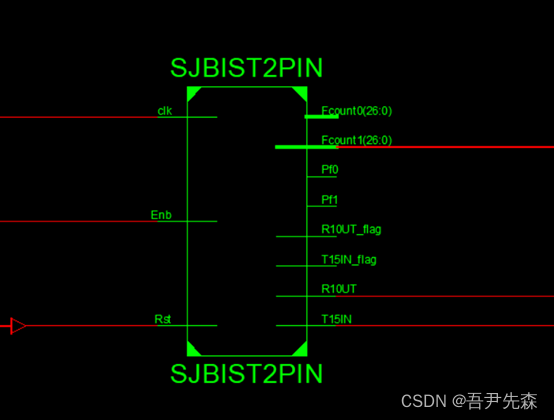
关于焊点检测(SJ-BIST)模块实现
关于焊点检测(SJ-BIST)模块实现 语言 :Verilg HDL 、VHDL EDA工具:ISE、Vivado、Quartus II 关于焊点检测(SJ-BIST)模块实现一、引言二、焊点检测功能的实现方法(1) 输入接口&#x…...

关于修改Python中pip默认安装路径的终极方法
别想了,终极方法就是手动复制,不过我可以给你参考一下手动复制的方法 关于手动移动pip安装包的方法 别想了,终极方法就是手动复制,不过我可以给你参考一下手动复制的方法一、首先确认一下pip默认安装路径二、再确认一下需要移动到…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
