2024.6.9刷题记录
目录
一、1103. 分糖果 II
1.模拟
2.数学
二、312. 戳气球
1.递归-记忆化搜索
2.区间dp
三、2. 两数相加
1.迭代
2.递归-新建节点
3.递归-原节点
四、4. 寻找两个正序数组的中位数
1.堆
2.双指针+二分
五、5. 最长回文子串
1.动态规划
2.中心扩展算法
六、6. Z 字形变换
1.模拟-规律
2.巧设flag
七、7. 整数反转
1.模拟
2.考虑溢出问题-模拟一下(错误代码)
一、1103. 分糖果 II
1.模拟
class Solution:def distributeCandies(self, candies: int, num_people: int) -> List[int]:# 模拟ans = [0] * num_peoplenum = 1while candies > 0:i = (num - 1) % num_peopleans[i] += min(num, candies)candies -= numnum += 1return ans2.数学
来自灵神题解(. - 力扣(LeetCode))。将添加操作分为“完整行”、“完整数”(最后一行中)、“不完整数”(最后一格)三个部分进行处理。
class Solution:def distributeCandies(self, candies: int, num_people: int) -> List[int]:# 数学# m = sqrt(8 * candies + 1) - 1) // 2 # 是错误的,当被除数为浮点数时,整除结果还是为浮点数m = int((sqrt(8 * candies + 1) - 1) / 2) # 前面完整的项数k, extra = divmod(m, num_people)ans = [(k - 1) * k * num_people // 2 + k * (i + 1) + \(k * num_people + i + 1 if i < extra else 0) \for i in range(num_people)]ans[extra] += candies - m * (m + 1) // 2return ans二、312. 戳气球
1.递归-记忆化搜索
来自官方题解(. - 力扣(LeetCode))。
class Solution:def maxCoins(self, nums: List[int]) -> int:# 递归-记忆化搜索# 逆向思维,将搓破气球改为放入气球n = len(nums)val = [1] + nums + [1]@cachedef solve(left: int, right: int) -> int:# 开区间,返回最大数量if left >= right - 1:# 空区间return 0best = 0for i in range(left + 1, right):# 遍历区间值得最大值total = val[left] * val[i] * val[right]# 在区间内放入一个,左右都是固定的total += solve(left, i) + solve(i, right) # 在左右分别放入best = max(best, total)return bestreturn solve(0, n + 1) # 现在是针对于val数组2.区间dp
来自官方题解。
class Solution:def maxCoins(self, nums: List[int]) -> int:# 区间dp# 使用二维数组表示区间n = len(nums)dp = [[0] * (n + 2) for _ in range(n + 2)]val = [1] + nums + [1]# dp要由小到大蔓延for i in range(n - 1, -1, -1):# 开区间, j - i > 1for j in range(i + 2, n + 2):for k in range(i + 1, j):total = val[i] * val[k] * val[j]total += dp[i][k] + dp[k][j]dp[i][j] = max(dp[i][j], total)return dp[0][n + 1]三、2. 两数相加
1.迭代
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:# 迭代carry = 0dummy = ListNode()cur = dummywhile l1 or l2 or carry:if l1: carry += l1.vall1 = l1.nextif l2:carry += l2.vall2 = l2.nextcur.next = ListNode(val = carry % 10)cur = cur.nextcarry //= 10return dummy.next2.递归-新建节点
判断边界的时候只想着有carry的情况,而没有返回无carry的情况(None)导致运行超时,修改后运行通过。我当时还以为我递归写错了,参考了灵神的递归才发现问题。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:# 递归-新建节点def addTwo(l1, l2, carry = 0):if not l1 and not l2:return ListNode(val = carry) if carry else Nonecarry += (l1.val if l1 else 0) + (l2.val if l2 else 0)nxt = addTwo(l1.next if l1 else None, l2.next if l2 else None, carry // 10)return ListNode(val = carry % 10, next = nxt)return addTwo(l1, l2)3.递归-原节点
来自灵神题解(. - 力扣(LeetCode))。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode], carry = 0) -> Optional[ListNode]:# 递归-原节点# 均在l1表的基础上修改if not l1 and not l2:# 这里是关键,一定还得记得Nonereturn ListNode(val = carry) if carry else Noneif not l1:l1, l2 = l2, l1carry += l1.val + (l2.val if l2 else 0)l1.val = carry % 10l1.next = self.addTwoNumbers(l1.next, l2.next if l2 else None, carry // 10)return l1四、4. 寻找两个正序数组的中位数
1.堆
时复O(m + n), 空复O(m + n)。但是堆没有运用到本身已经有序的这一特点。
class Solution:def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:# 堆# 时复O(m + n), 空复O(m + n)m, n = len(nums1), len(nums2)q = nums1 + nums2heapq.heapify(q) # 原地堆化for _ in range((m + n - 1) // 2):heapq.heappop(q)return (heapq.heappop(q) + heapq.heappop(q)) / 2 if (m + n) % 2 == 0 else heapq.heappop(q)2.双指针+二分
时复O(log(min(m,n))),空复O(1)。来自题解(. - 力扣(LeetCode))。题解作者使用的是左闭右开区间,博主本人二分习惯使用闭区间,所以改为了闭区间写法。
class Solution:def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:# 双指针+二分# 时复O(log(min(m,n))),空复O(1)n1 = len(nums1)n2 = len(nums2)if n1 > n2:# 使查找较短数组return self.findMedianSortedArrays(nums2, nums1)k = (n1 + n2 + 1) // 2left = 0right = n1 - 1# 二分留在左边的nums1的个数while left <= right:# 闭区间m1 = (left + right) // 2m2 = k - m1 # 留在左边的nums2的个数# 当nums2划分多了的时候,左边的nums2最后一位是大于右边nums1的第一位if nums1[m1] < nums2[m2 - 1]: # checkleft = m1 + 1else:right = m1 - 1m1 = leftm2 = k - m1# 左边最大值# m1是个数,m1 - 1是下标# 注意,划分个数是确定了,但是大小没有确定c1 = max(nums1[m1 - 1] if m1 > 0 else float("-inf"), nums2[m2 - 1] if m2 > 0 else float("-inf"))if (n1 + n2) % 2 == 1:return c1c2 = min(nums1[m1] if m1 < n1 else float("inf"), nums2[m2] if m2 < n2 else float("inf"))return (c1 + c2) / 2五、5. 最长回文子串
不会,均来自官方题解(. - 力扣(LeetCode))。
1.动态规划
class Solution:def longestPalindrome(self, s: str) -> str:# 动态规划n = len(s)if n < 2:return smax_len = 1begin = 0# dp[i][j] 表示 s[i..j] 是否是回文串dp = [[False] * n for _ in range(n)]# 记得初始化for i in range(n):# 长度为1是回文dp[i][i] = True# 递推# 先枚举子串长度,从小到大for L in range(2, n + 1):# 枚举左边界for i in range(n):# 右边界j - i + 1 = Lj = L + i - 1# 右边界越界if j >= n:breakif s[i] != s[j]:dp[i][j] = Falseelse:if j - i < 3:dp[i][j] = Trueelse:dp[i][j] = dp[i + 1][j - 1] # 内串是否为回文串# 更新if dp[i][j] and j - i + 1 > max_len:max_len = j - i + 1begin = i # 记录起始位置,方便返回return s[begin: begin + max_len]2.中心扩展算法
class Solution:def expandAroundCenter(self, s: str, left: int, right: int):# 中心扩展算法while left >= 0 and right < len(s) and s[left] == s[right]:left -= 1right += 1return left + 1, right - 1 # 符号条件的def longestPalindrome(self, s: str) -> str:# 中心扩展算法start, end = 0, 0for i in range(len(s)):# 边界条件1,初始中心串长度为1left1, right1 = self.expandAroundCenter(s, i, i)# 边界条件2,初始中心串长度为2left2, right2 = self.expandAroundCenter(s, i, i + 1)if right1 - left1 > end - start:start, end = left1, right1if right2 - left2 > end - start:start, end = left2, right2return s[start: end + 1]六、6. Z 字形变换
1.模拟-规律
class Solution:def convert(self, s: str, numRows: int) -> str:# 模拟-规律# 将每一条竖线(斜线)分开看# 第一行和最后一行为重叠部分if numRows == 1:return sans = []n = len(s)for row in range(numRows):if row != 0 and row != numRows - 1:# 普通竖线(斜线)for j in range(row, n, (numRows - 1)* 2):# 竖线ans.append(s[j])# 斜线idx = j + 2 * (numRows - 1 - row)if idx < n:ans.append(s[idx])else:# 第一行和最后一行,重叠部分,特判for j in range(row, n, (numRows - 1)* 2):ans.append(s[j])return ''.join(ans)2.巧设flag
来自题解(. - 力扣(LeetCode))。很妙!
class Solution:def convert(self, s: str, numRows: int) -> str:# 巧设flag# 行数先增后减,使用flag模拟if numRows < 2:return sans = ["" for _ in range(numRows)]i, flag = 0, -1 # flag代表增减ifor c in s:ans[i] += c# 边界处转换if i == 0 or i == numRows - 1: flag = -flagi += flagreturn ''.join(ans)七、7. 整数反转
1.模拟
python一般不会出现溢出的问题,所以实际上并没有受到限制,题主也就并没有答到考点。
class Solution:def reverse(self, x: int) -> int:# 模拟x, flag = (x, 1) if x >= 0 else (-x, -1)ans = 0while x > 0:ans *= 10 # 进位ans += x % 10x //= 10return flag * ans if - 2 ** 31 <= flag * ans <= 2 ** 31 - 1 else 02.考虑溢出问题-模拟一下(错误代码)
来自题解(. - 力扣(LeetCode)),讲解非常通俗易懂。虽然python不用考虑,但是还是应该学习一下。
class Solution:def reverse(self, x: int) -> int:# 考虑溢出问题-模拟一下(错误代码)# 由于python的自动转换机制,并不能实现# 该代码是运行错误的INT_MAX_VALUE = 2 * 31 - 1 # 错误问题出在这里INT_MIN_VALUE = - 2 ** 31ans = 0while x != 0:pop = x % 10if ans > INT_MAX_VALUE // 10 or (ans == INT_MAX_VALUE // 10 and pop > 7):return 0if ans < INT_MIN_VALUE // 10 or (ans == INT_MIN_VALUE // 10 and pop < -8):return 0ans = ans * 10 + popx //= 10return ans完
感谢你看到这里!一起加油吧!
相关文章:

2024.6.9刷题记录
目录 一、1103. 分糖果 II 1.模拟 2.数学 二、312. 戳气球 1.递归-记忆化搜索 2.区间dp 三、2. 两数相加 1.迭代 2.递归-新建节点 3.递归-原节点 四、4. 寻找两个正序数组的中位数 1.堆 2.双指针二分 五、5. 最长回文子串 1.动态规划 2.中心扩展算法 六、6. Z…...
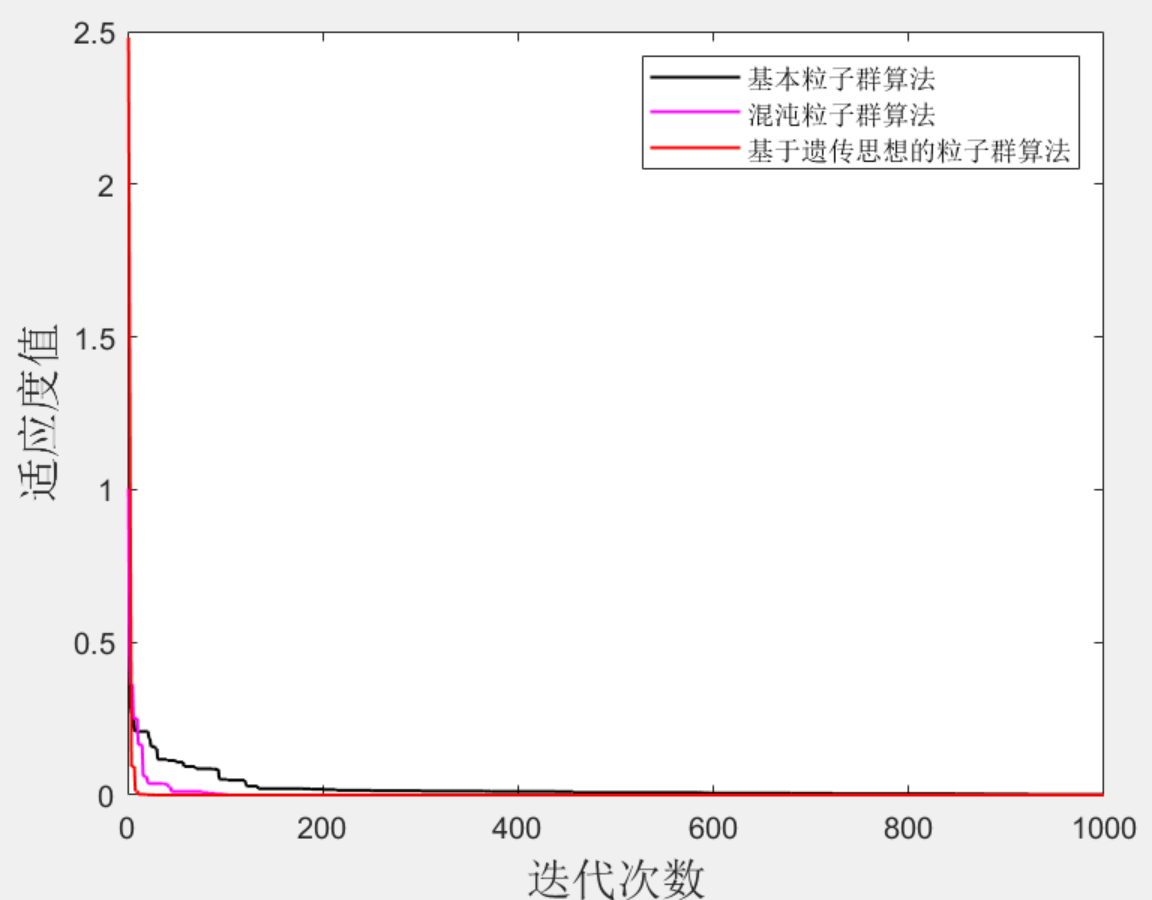
Matlab|遗传粒子群-混沌粒子群-基本粒子群
目录 1 主要内容 2 部分代码 3 效果图 4 下载链接 1 主要内容 很多同学在发文章时候最犯愁的就是创新点创新点创新点(重要的事情说三遍),对于采用智能算法的模型,可以采用算法改进的方式来达到提高整个文章创新水平的目的&…...
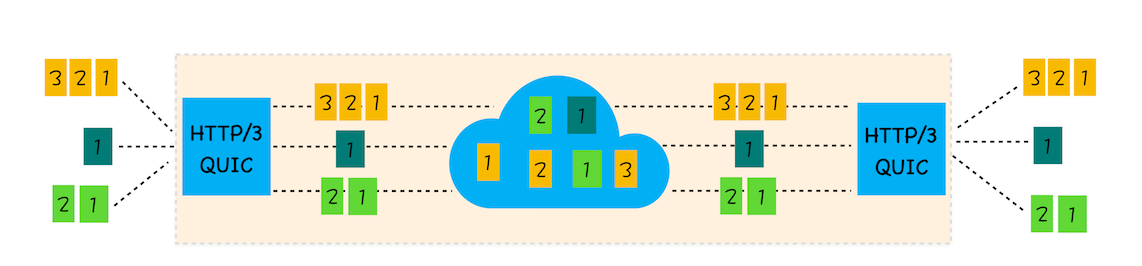
31|HTTP3:甩掉TCP、TLS 的包袱,构建高效网络
前面两篇文章我们分析了HTTP/1和HTTP/2,在HTTP/2出现之前,开发者需要采取很多变通的方式来解决HTTP/1所存在的问题,不过HTTP/2在2018年就开始得到了大规模的应用,HTTP/1中存在的一大堆缺陷都得到了解决。 HTTP/2的一个核心特性是…...
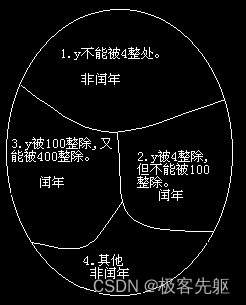
2 程序的灵魂—算法-2.2 简单算法举例-【例 2.3】
【例 2.3】判定 2000 — 2500 年中的每一年是否闰年,将结果输出。 润年的条件: 1. 能被 4 整除,但不能被 100 整除的年份; 2. 能被 100 整除,又能被 400 整除的年份; 设 y 为被检测的年份,则算法可表示如下…...
模块)
Python中的上下文管理器(contextlib)模块
Python中的contextlib模块提供了一些用于创建和管理上下文管理器(context managers)的工具。上下文管理器是实现了__enter__()和__exit__()方法的对象,它们通常用于确保在代码块执行前后执行某些操作,比如资源获取与释放、设置和重…...

C语言:定义和使用结构体变量
定义和使用结构体变量 介绍基础用法1.定义结构体2. 声明结构体变量3. 初始化和访问结构体成员4. 使用指针访问结构体成员5. 使用结构体数组 高级用法6. 嵌套结构体7. 匿名结构体8. 结构体和动态内存分配9. 结构体作为函数参数按值传递按引用传递 介绍 在C语言中,结…...

Vue3学习第二天记录
Vue3学习第二天记录 背景说明截图记录一个简单的JS文件Vue3的watch()函数Vue3的toRef()/toRefs()函数前端数据类型的分类前端写一个对外暴露的函数前端的...语法Vue3中watch()函数的总结Vue3中watchEffect()函数Vue3中watch()函数的坑Vue3中computed()函数 背景 最近在学习尚硅…...
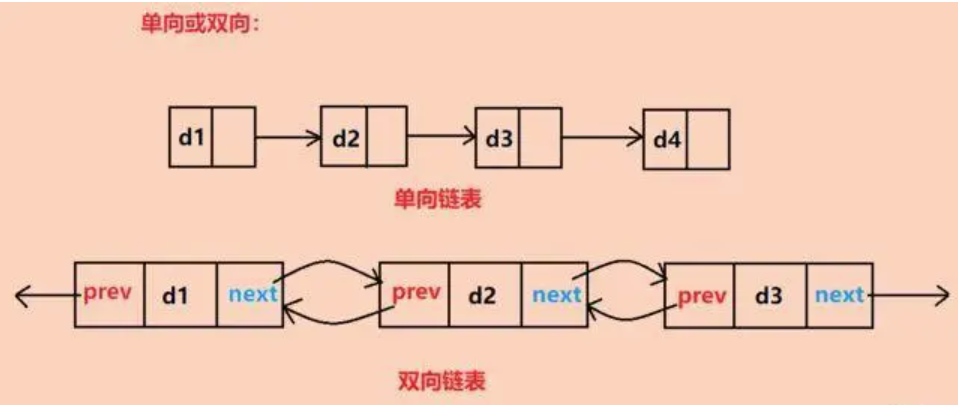
C语言:双链表
一、什么是双链表? 双链表,顾名思义,是一种每个节点都包含两个链接的链表:一个指向下一个节点,另一个指向前一个节点。这种结构使得双链表在遍历、插入和删除操作上都表现出色。与单链表相比,双链表不仅可以…...

Java物业管理系统+数据库应用程序开发[JavaSE+JDBC+idea控制台+MySQL]
背景: 使用JavaSEJDBCMySQL技术实现一个物业管理系统,具体要求如下 物业管理系统需求: 需求分析 1.1用户需求分析 在进入系统之前,要进行身份确认,只有用户名和用户密码都相符的用户方可进入本系统,为…...
未在本地计算机上注册“Microsoft.ACE.OLEDB.12.0”提供程序。.net 读取excel的时候报错(实测有效)
1. 下载AccessDatabaseEngine.exe 下载链接 添加链接描述 2. office excel是64为的需要安装【AccessDatabaseEngine.exe】、32位的【AccessDatabaseEngine_X64.exe】 3. 我的是64为,跳过32位安装检测 1. 找到下载的安装包 2.输入安装包文件全称并在后面加上/pas…...
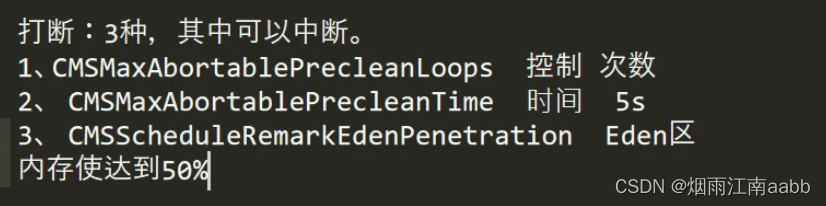
JVM垃圾收集器和性能调优
目标: 1.JVM垃圾收集器有哪几种? 2.CMS垃圾收集器回收步骤。 一、JVM常见的垃圾回收器 为什么垃圾回收的时候需要STW? 标记垃圾的时候,如果不STW,可能用户线程就会不停的产生垃圾。 1.1 单线程收集 Serial和SerialOld使用单…...
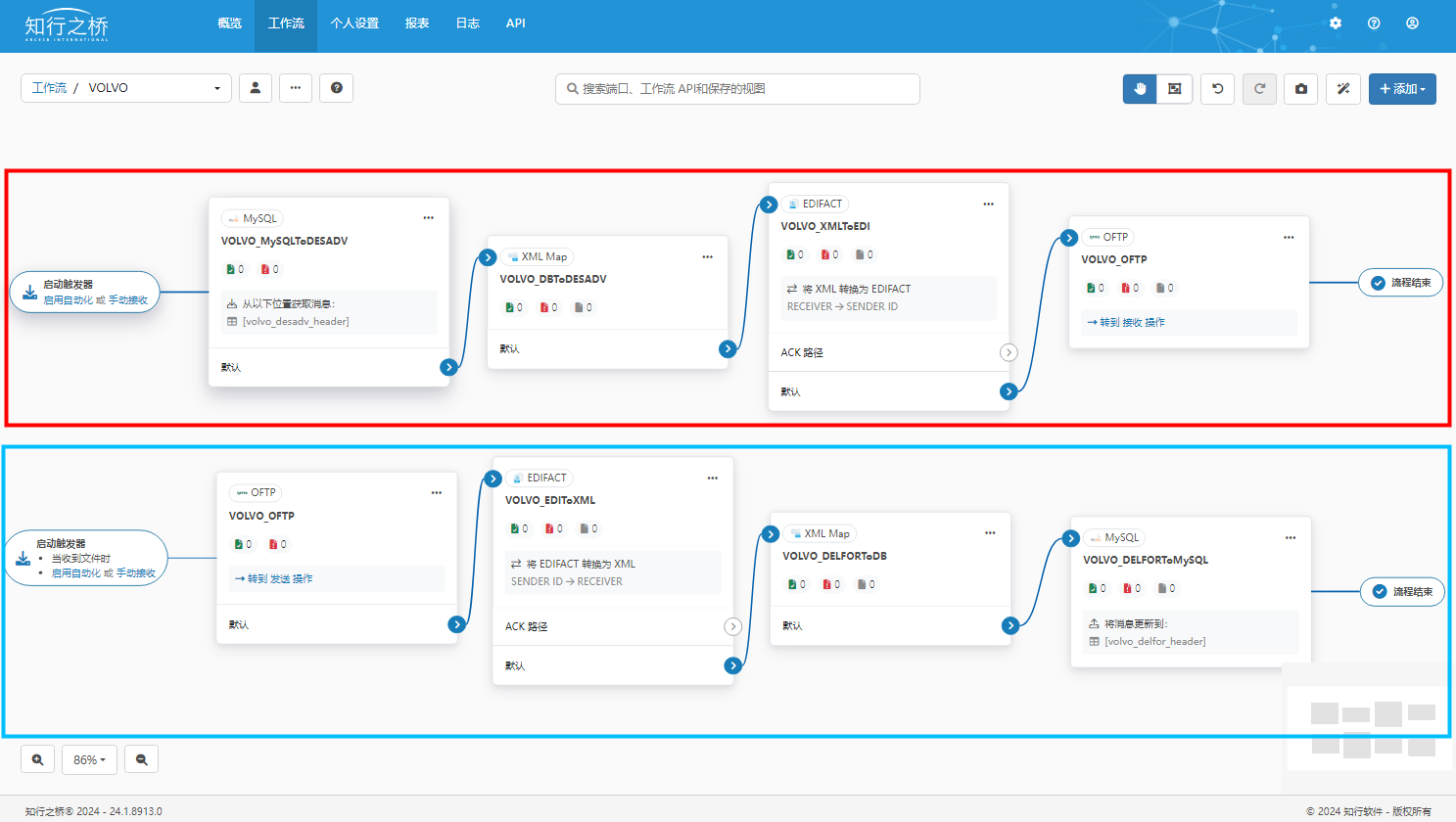
汽车EDI——Volvo EDI 项目案例
项目背景 作为Volvo的长期合作伙伴,C公司收到Volvo的EDI对接邀请,需要实现EDI对接。C公司将会面临哪些挑战?又应该相应地选择何种EDI解决方案呢? 汽车行业强调供需双方的高效协同(比如研发设计、生产计划、物流信息等…...

Qt应用程序发布
一、静态编译发布 1.0:以Release模式构建工程 1.1:查看当前构建生成路径,并将所生成的.exe单独拷贝出来 1.2:将可执行文件*.exe拷贝至任一目标文件夹:D:\Temporary\QQIF 2:查看安装Qt时发布工具windeployqt.exe所在的目录 windeployqt.exe在Qt开发套件的bin目录下。Qt的每…...

Python 机器学习 基础 之 【常用机器学习库】 NumPy 数值计算库
Python 机器学习 基础 之 【常用机器学习库】 NumPy 数值计算库 目录 Python 机器学习 基础 之 【常用机器学习库】 NumPy 数值计算库...
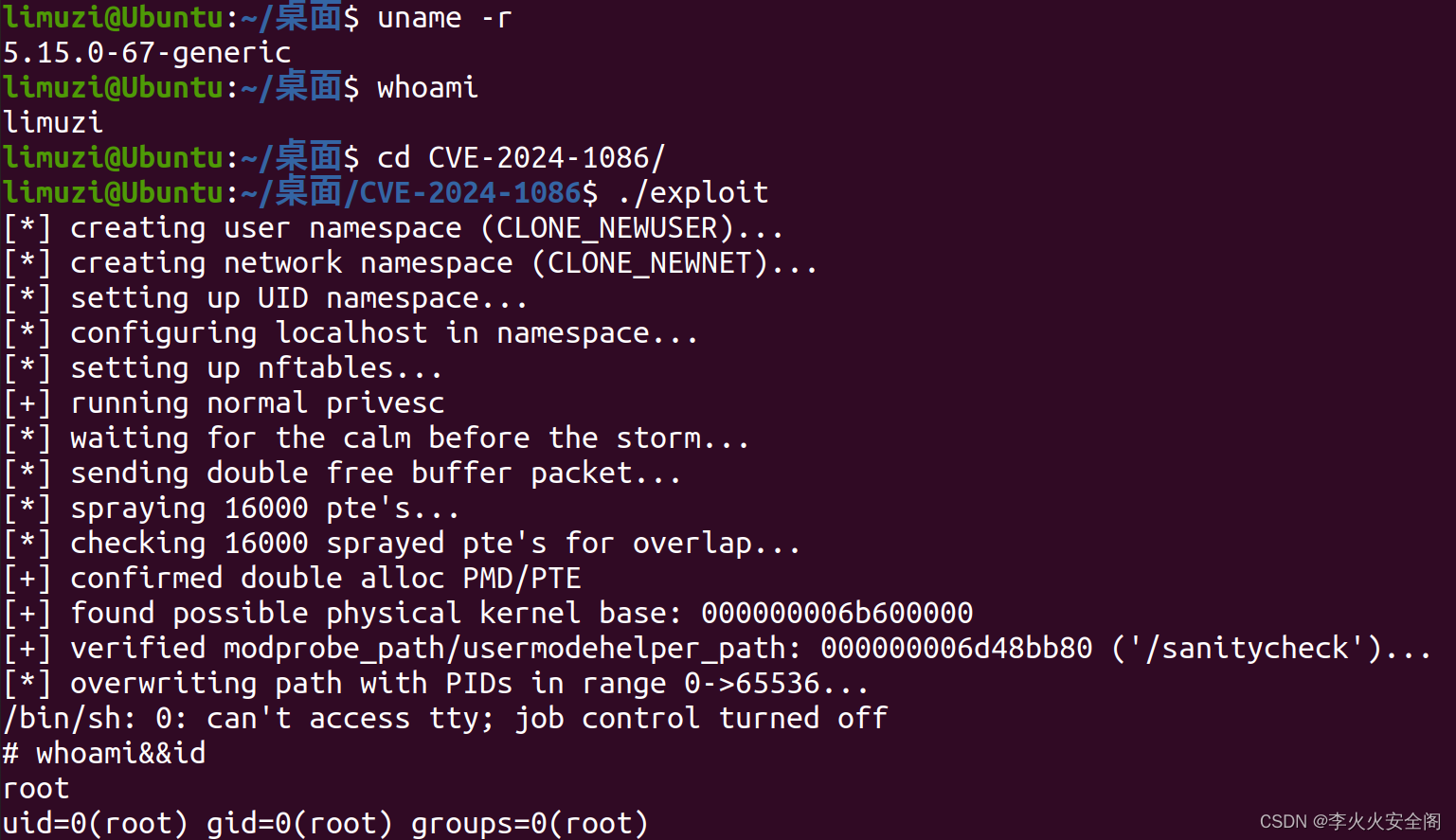
Linux Kernel nf_tables 本地权限提升漏洞(CVE-2024-1086)
文章目录 前言声明一、netfilter介绍二、漏洞成因三、漏洞危害四、影响范围五、漏洞复现六、修复方案临时解决方案升级修复方案 前言 2024年1月,各Linux发行版官方发布漏洞公告,修复了一个 netfilter:nf_tables 模块中的释放后重用漏洞(CVE-…...

[word] word如何清除超链接 #媒体#笔记#知识分享
word如何清除超链接 办公中,少不了使用word,这个是大家必备的软件,今天给大家分享下word如何清除超链接的操作办法,一起来学习下吧! 1、清除所有超链接 按下组合键CtrlshiftF9,就可以将网上复制带有超链…...
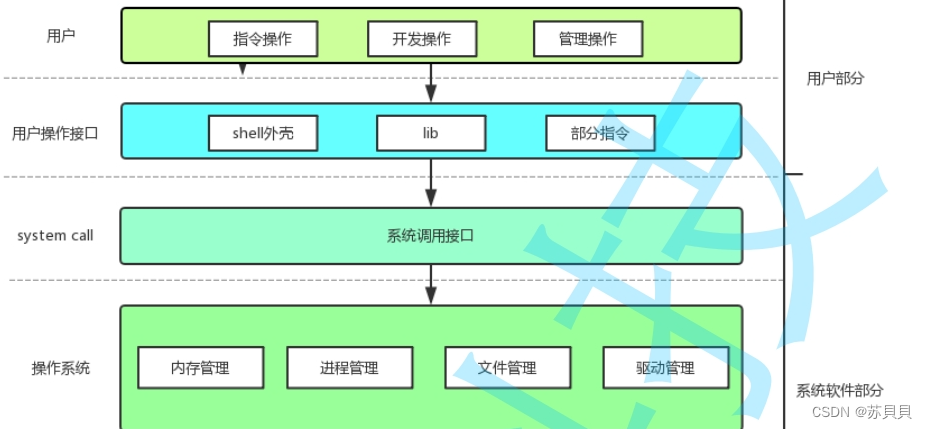
【Linux】进程(9):进程控制1
大家好,我是苏貝,本篇博客带大家了解Linux进程(9)进程控制1,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 1 fork函数2 进程终止(A)终止是…...
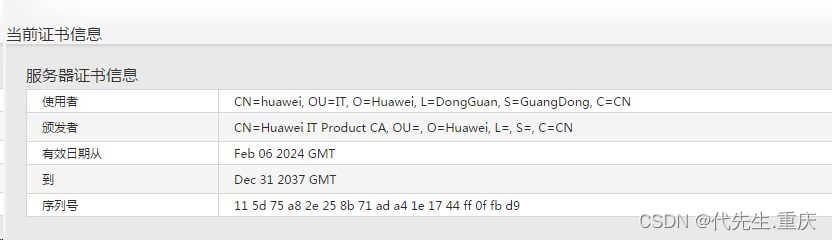
华为RH2288H V3服务器iBMC的SSL证书续期
本文对华为RH2288H V3服务器iBMC的SSL证书续期,以避名登录告警提示及主机状态异常。 一、检查现网服务器iBMC的SSL证书到期时间 登录iBMC,点击配置--SSL证书,如下: 可以看到本服务器SSL证书将于今年7月22日到期。 二、联系厂家…...

ubuntu开机黑屏
BusyBox v1.30.1 (Ubuntu 1:1.30.1-4ubuntu6.1) built-in shell (ash) Enter help for a list of built-in commands. 解决: help 看看哪个盘出问题了 fsck -y /dev/sda1 (出问题的磁盘/分区) reboot 就可以进入系统了 fsck命令…...

【risc-v】arm和riscv有什么关系或者联系?
ARM和RISC-V都是基于精简指令集计算(RISC)原理的处理器架构,它们在设计理念上有一定的联系,但同时存在一些关键的区别: 设计理念:ARM和RISC-V都采用了RISC的核心设计原则,即通过简化指令集来提高…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...
