IGraph使用实例——线性代数计算（blas）

 1 概述

在图论中，BLAS（Basic Linear Algebra Subprograms）并不直接应用于图论的计算，而是作为一套线性代数计算中通用的基本运算操作函数集合，用于进行向量和矩阵的基本运算。然而，这些基本运算在图论的相关计算中可能会被用到，尤其是涉及到矩阵运算的时候。

BLAS主要包含以下三个级别的函数：

1. Level 1 BLAS函数：
   • 处理单一向量的线性运算，如向量的加、减、数乘等。
   • 处理两个向量的二元运算，如点积、向量外积等。
2. Level 2 BLAS函数：
   • 处理矩阵与向量的运算，如矩阵与向量的乘积、矩阵的秩1更新等。
   • 包含线性方程求解计算，如使用高斯消元法解线性方程组。
3. Level 3 BLAS函数：
   • 包含矩阵与矩阵的运算，如矩阵乘法、矩阵的三角分解等。

在图论中，如果涉及到矩阵表示的图（如邻接矩阵）、线性方程组的求解（如网络流问题中的势能法）或者特征值问题（如图的谱分析）等，就可能会使用到BLAS库中的函数。

2 运行环境

操作系统：win10 64位

编程语言：C/C++

编译平台：vs2019  x64 debug | release

igraph版本： 0.10.12

3 示例代码

在IGraph中的blas.c文件中提供了丰富的功能来处理图和网络数据结构。这个特定的文件包含了一些使用BLAS（Basic Linear Algebra Subprograms）库的函数，用于执行线性代数操作，如矩阵-向量乘法、矩阵-矩阵乘法、向量的欧几里得范数计算和向量的点积。

文件中定义了几个函数，每个函数都与特定的线性代数操作相关：

1. igraph_blas_dgemv：执行矩阵-向量乘法，使用BLAS库中的dgemv函数。它支持矩阵的转置操作，并允许用户指定alpha和beta系数。

2. igraph_blas_dgemm：执行矩阵-矩阵乘法，使用BLAS库中的dgemm函数。它同样支持矩阵的转置操作，并允许用户指定alpha和beta系数。

3. igraph_blas_dgemv_array：与igraph_blas_dgemv类似，但是它接受C语言数组作为输入，而不是IGraph库中的向量对象。

4. igraph_blas_dnrm2：计算向量的欧几里得范数，使用BLAS库中的dnrm2函数。

5. igraph_blas_ddot：计算两个向量的点积，使用BLAS库中的ddot函数。

3.1 示例1

 在下列代码中使用了igraph库，特别是它的线性代数部分（通过igraph_blas函数集）来进行一些基本的矩阵和向量运算。

#include <igraph.h>  // 引入igraph库的头文件  int main(void) {  // 定义igraph的矩阵和向量对象  igraph_matrix_t m;  igraph_vector_t x, y, z;  igraph_real_t xz, xx;  // 用于存储计算结果的两个实数变量  // 初始化向量x，包含3个元素，分别为1.0, 2.0, 3.0  igraph_vector_init_real(&x, 3, 1.0, 2.0, 3.0);  // 初始化向量y，包含4个元素，分别为4.0, 5.0, 6.0, 7.0  // 注意：虽然y之后会被用于计算，但这里先初始化为一些值  igraph_vector_init_real(&y, 4, 4.0, 5.0, 6.0, 7.0);  // 初始化向量z，包含3个元素，分别为-1.0, 0.0, 0.5  igraph_vector_init_real(&z, 3, -1.0, 0.0, 0.5);  // 初始化一个4x3的矩阵m，并为其赋值  igraph_matrix_init(&m, 4, 3);  // 填充矩阵m的元素  MATRIX(m, 0, 0) = 1;MATRIX(m, 0, 1) = 2;MATRIX(m, 0, 2) = 3;MATRIX(m, 1, 0) = 2;MATRIX(m, 1, 1) = 3;MATRIX(m, 1, 2) = 4;MATRIX(m, 2, 0) = 3;MATRIX(m, 2, 1) = 4;MATRIX(m, 2, 2) = 5;MATRIX(m, 3, 0) = 4;MATRIX(m, 3, 1) = 5;MATRIX(m, 3, 2) = 6;// 计算 2 * m.x + 3 * y，并将结果存储在y中  // 注意：这里的操作会改变y的内容  igraph_blas_dgemv(/* transpose= */ 0, /* alpha= */ 2, &m, &x, /* beta= */ 3, &y);  // 打印向量y的新内容  igraph_vector_print(&y);  // 计算向量x的模的平方（即x与自身的点积），存储在xx中  igraph_blas_ddot(&x, &x, &xx);  // 计算向量x和z的点积，存储在xz中  igraph_blas_ddot(&x, &z, &xz);  // 打印结果  printf("x.x = %g, x.z = %g\n", xx, xz);  // 销毁之前创建的矩阵和向量对象，释放内存  igraph_matrix_destroy(&m);  igraph_vector_destroy(&z);  igraph_vector_destroy(&y);  igraph_vector_destroy(&x);  return 0;  
}

3.2 示例2

 以下代码使用BLAS（Basic Linear Algebra Subprograms）库中的dgemm（Double-precision General Matrix Multiply）函数来执行两个矩阵的乘法，并将结果存储在第三个矩阵中。

// 引入igraph库的头文件  
#include <igraph.h>  int main(void) {  // 声明三个igraph_matrix_t类型的变量a, b, c，用于存储矩阵  igraph_matrix_t a, b, c;  // 初始化一个2x2的矩阵a，并为其分配内存  igraph_matrix_init(&a, 2, 2);  // 设置矩阵a的元素  MATRIX(a, 0, 0) = 1;  // a[0][0] = 1  MATRIX(a, 0, 1) = 2;  // a[0][1] = 2  MATRIX(a, 1, 0) = 3;  // a[1][0] = 3  MATRIX(a, 1, 1) = 4;  // a[1][1] = 4  // 初始化一个2x2的矩阵b，并为其分配内存  igraph_matrix_init(&b, 2, 2);  // 设置矩阵b的元素  MATRIX(b, 0, 0) = 5;  // b[0][0] = 5  MATRIX(b, 0, 1) = 6;  // b[0][1] = 6  MATRIX(b, 1, 0) = 7;  // b[1][0] = 7  MATRIX(b, 1, 1) = 8;  // b[1][1] = 8  // 初始化一个2x2的矩阵c，用于存储a和b的乘法结果  igraph_matrix_init(&c, 2, 2);  // 使用igraph_blas_dgemm函数计算a和b的乘积，并将结果乘以0.5后存储在c中  // 第一个和第二个参数分别是矩阵a和b的alpha（这里是1，即不缩放）  // 第三个参数是缩放因子（这里是0.5）  // 第四和第五个参数是矩阵a和b的指针  // 第六个参数是矩阵c的beta（这里是0，即不使用c的原始值）  // 第七个参数是结果矩阵c的指针  igraph_blas_dgemm(1, 1, 0.5, &a, &b, 0, &c);  // 打印矩阵c的内容  igraph_matrix_printf(&c, "%g");  // 释放矩阵a, b, c所占用的内存  igraph_matrix_destroy(&a);  igraph_matrix_destroy(&b);  igraph_matrix_destroy(&c);  // 程序正常退出  return 0;  
}

4 运行结果

4.1 结果1

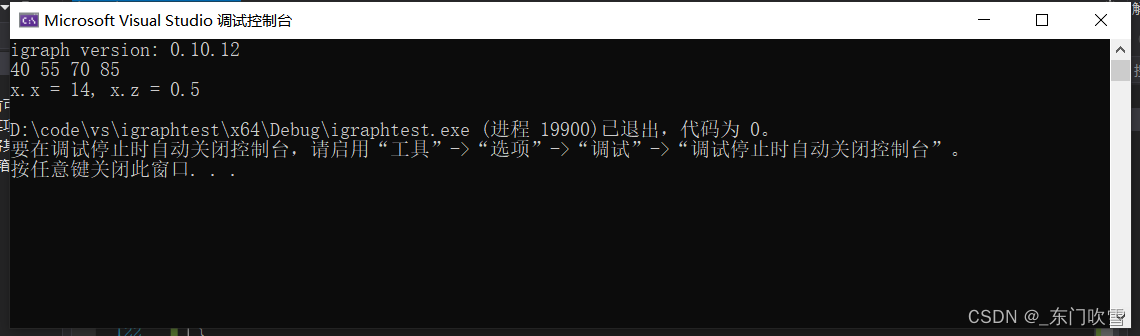
首先，我们初始化了几个向量x, y, z和一个矩阵m。然后为矩阵m赋值了一个4x3的矩阵。

在第一个igraph_blas_dgemv函数调用中，我们试图计算2 * m * x + 3 * y并将结果存储在y中。但是，请注意，由于igraph_blas_dgemv的默认操作是y = alpha * A * x + beta * y（其中A是矩阵，x和y是向量，alpha和beta是标量），因此，实际上是在更新y的值，而不是简单地计算结果。由于y的初始值不为零，这会影响最终结果。

y向量初始化为[4.0, 5.0, 6.0, 7.0]。在调用igraph_blas_dgemv后，y将被更新为2 * m * x + 3 * y。

矩阵m与向量x的乘法结果是一个4x1的向量，其值为[1*1 + 2*2 + 3*3, 2*1 + 3*2 + 4*3, 3*1 + 4*2 + 5*3, 4*1 + 5*2 + 6*3]，即[14, 20, 26, 32]。

然后，我们将这个结果与y的初始值相加，并乘以相应的系数：

• y[0] 变为 2 * 14 + 3 * 4.0 = 28 + 12 = 40
• y[1] 变为 2 * 20 + 3 * 5.0 = 40 + 15 = 55
• y[2] 变为 2 * 26 + 3 * 6.0 = 52 + 18 = 70
• y[3] 变为 2 * 32 + 3 * 7.0 = 64 + 21 = 85

因此，y向量的最终值是[40, 55, 70, 85]。

接下来，我们使用igraph_blas_ddot来计算x与x的点积（即x.x），以及x与z的点积（即x.z）。这些计算的结果是：

• x.x 是 [1.0, 2.0, 3.0] 与 [1.0, 2.0, 3.0] 的点积，即 1*1 + 2*2 + 3*3 = 14
• x.z 是 [1.0, 2.0, 3.0] 与 [-1.0, 0.0, 0.5] 的点积，即 1*(-1) + 2*0 + 3*0.5 = -1 + 1.5 = 0.5

因此输出x.x = 14, x.z = 0.5。

4.2 结果2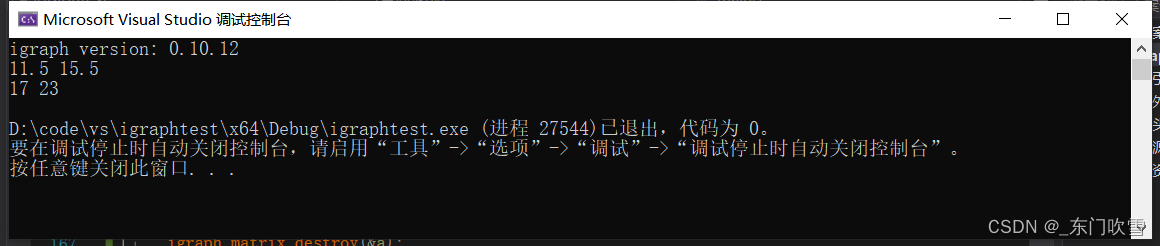 

根据矩阵乘法的定义和给定的代码，矩阵a和b的乘积再乘以0.5会得到矩阵c，其元素计算如下：

a = [1 2; 3 4]

b = [5 6; 7 8]

c = 0.5 * (a * b)

矩阵乘法a * b的结果为：

[1*5 + 2*7 1*6 + 2*8; 3*5 + 4*7 3*6 + 4*8] = [1 + 14 6 + 16; 15 + 28 18 + 32] = [15 22; 43 50]

然后，我们将这个结果乘以0.5得到矩阵c：

c = [15*0.5 22*0.5; 43*0.5 50*0.5] = [7.5 11; 21.5 25]

最后程序执行结果如下：

11.5 15.5

17 23