基于JavaScript 如何实现爬山算法以及优化方案
前言
爬山算法(Hill Climbing Algorithm)是一种常见的启发式搜索算法,常用于解决优化问题。其核心思想是从一个初始状态出发,通过逐步选择使目标函数值增大的邻近状态来寻找最优解。接下来,我们将通过 JavaScript 实现一个简单的爬山算法,帮助大家理解其原理和应用。
什么是爬山算法?
爬山算法的基本步骤如下:
- 从一个初始状态开始。
- 评估当前状态的目标函数值。
- 在当前状态的邻居中选择一个目标函数值更大的状态。
- 如果找到了更优的邻居,则移动到该邻居并重复步骤2和步骤3。
- 如果没有更优的邻居,则算法结束,当前状态即为局部最优解。
JavaScript 实现爬山算法
为了简单起见,我们将使用一个一维函数来进行优化。假设我们的目标函数是 f(x) = -x^2 + 4x,我们希望找到使该函数值最大的 x。
代码实现
// 定义目标函数
function objectiveFunction(x) {return -x * x + 4 * x;
}// 定义爬山算法函数
function hillClimbing(initialState, stepSize, maxIterations) {let currentState = initialState;let currentValue = objectiveFunction(currentState);for (let i = 0; i < maxIterations; i++) {let nextState = currentState + stepSize;let nextValue = objectiveFunction(nextState);if (nextValue > currentValue) {currentState = nextState;currentValue = nextValue;} else {// 尝试向另一方向移动nextState = currentState - stepSize;nextValue = objectiveFunction(nextState);if (nextValue > currentValue) {currentState = nextState;currentValue = nextValue;} else {// 没有更优的邻居,算法结束break;}}}return { state: currentState, value: currentValue };
}// 使用爬山算法寻找目标函数的最大值
let initialState = 0; // 初始状态
let stepSize = 0.1; // 步长
let maxIterations = 100; // 最大迭代次数let result = hillClimbing(initialState, stepSize, maxIterations);console.log(`最优状态: ${result.state}`);
console.log(`最优值: ${result.value}`);
代码解析
-
目标函数:
function objectiveFunction(x) {return -x * x + 4 * x; }这是我们要优化的目标函数。
-
爬山算法函数:
function hillClimbing(initialState, stepSize, maxIterations) {// 初始化当前状态和当前值let currentState = initialState;let currentValue = objectiveFunction(currentState);for (let i = 0; i < maxIterations; i++) {// 尝试向正方向移动let nextState = currentState + stepSize;let nextValue = objectiveFunction(nextState);if (nextValue > currentValue) {currentState = nextState;currentValue = nextValue;} else {// 尝试向反方向移动nextState = currentState - stepSize;nextValue = objectiveFunction(nextState);if (nextValue > currentValue) {currentState = nextState;currentValue = nextValue;} else {// 没有更优的邻居,算法结束break;}}}return { state: currentState, value: currentValue }; }在这个函数中,我们定义了爬山算法的逻辑,包括初始化状态、评估邻居状态,并选择最优邻居的过程。
-
运行算法:
let initialState = 0; // 初始状态 let stepSize = 0.1; // 步长 let maxIterations = 100; // 最大迭代次数let result = hillClimbing(initialState, stepSize, maxIterations);console.log(`最优状态: ${result.state}`); console.log(`最优值: ${result.value}`);最后,我们设置初始状态、步长和最大迭代次数,并运行爬山算法。打印出最优状态和最优值。
改进措施
虽然基本的爬山算法已经能够解决一些简单的优化问题,但它存在一些不足,如容易陷入局部最优解和对初始状态敏感。为了提升算法的性能,我们可以进行一些改进和扩展。
1. 随机重启爬山算法
随机重启爬山算法(Random Restart Hill Climbing)通过多次随机选择初始状态来避免陷入局部最优解。每次从不同的初始状态开始运行爬山算法,并记录每次运行的最优解,最终返回所有运行中的全局最优解。
function randomRestartHillClimbing(numRestarts, stepSize, maxIterations) {let bestState = null;let bestValue = -Infinity;for (let i = 0; i < numRestarts; i++) {let initialState = Math.random() * 10 - 5; // 生成随机初始状态let result = hillClimbing(initialState, stepSize, maxIterations);if (result.value > bestValue) {bestState = result.state;bestValue = result.value;}}return { state: bestState, value: bestValue };
}let numRestarts = 10; // 重启次数
let result = randomRestartHillClimbing(numRestarts, stepSize, maxIterations);console.log(`全局最优状态: ${result.state}`);
console.log(`全局最优值: ${result.value}`);
2. 模拟退火算法
模拟退火算法(Simulated Annealing)是一种带有随机性的优化算法,通过允许算法跳出局部最优解来寻找全局最优解。模拟退火的核心在于控制温度的下降,在高温时允许接受较差解,在低温时趋向于接受更优解。
function simulatedAnnealing(initialState, stepSize, maxIterations, initialTemperature, coolingRate) {let currentState = initialState;let currentValue = objectiveFunction(currentState);let temperature = initialTemperature;for (let i = 0; i < maxIterations; i++) {let nextState = currentState + (Math.random() * 2 - 1) * stepSize;let nextValue = objectiveFunction(nextState);if (nextValue > currentValue || Math.exp((nextValue - currentValue) / temperature) > Math.random()) {currentState = nextState;currentValue = nextValue;}// 降低温度temperature *= coolingRate;}return { state: currentState, value: currentValue };
}let initialTemperature = 100;
let coolingRate = 0.99;
let resultSA = simulatedAnnealing(initialState, stepSize, maxIterations, initialTemperature, coolingRate);console.log(`模拟退火获得的最优状态: ${resultSA.state}`);
console.log(`模拟退火获得的最优值: ${resultSA.value}`);
实际应用场景
爬山算法及其改进版本在实际生活中有广泛的应用,如:
- 路径规划:寻找到达目的地的最短路径。
- 参数优化:在机器学习模型训练中,优化模型参数以提高模型性能。
- 组合优化:解决背包问题、旅行商问题等组合优化问题。
结语
通过上述代码,我们可以看到爬山算法在解决一维优化问题上的应用。虽然爬山算法简单易懂,但它只能找到局部最优解,不能保证找到全局最优解。在实际应用中,我们通常会结合其他策略(如多次随机初始化)来增强其性能。
爬山算法是理解启发式搜索算法的一个重要起点。尽管它有局限性,但其简单性和直观性使其在许多实际问题中仍然具有价值。通过改进和结合其他技术,如随机重启和模拟退火,我们可以提升算法性能,从而在更复杂的优化问题中找到更优解。
相关文章:

基于JavaScript 如何实现爬山算法以及优化方案
前言 爬山算法(Hill Climbing Algorithm)是一种常见的启发式搜索算法,常用于解决优化问题。其核心思想是从一个初始状态出发,通过逐步选择使目标函数值增大的邻近状态来寻找最优解。接下来,我们将通过 JavaScript 实现…...

Redisson分布式锁原理解析
前言 首先Redis执行命令是单线程的,所以可以利用Redis实现分布式锁,而对于Redis单线程的问题,是其线程模型的问题,本篇重点是对目前流行的工具Redisson怎么去实现的分布式锁进行深入理解;开始之前,我们可以…...
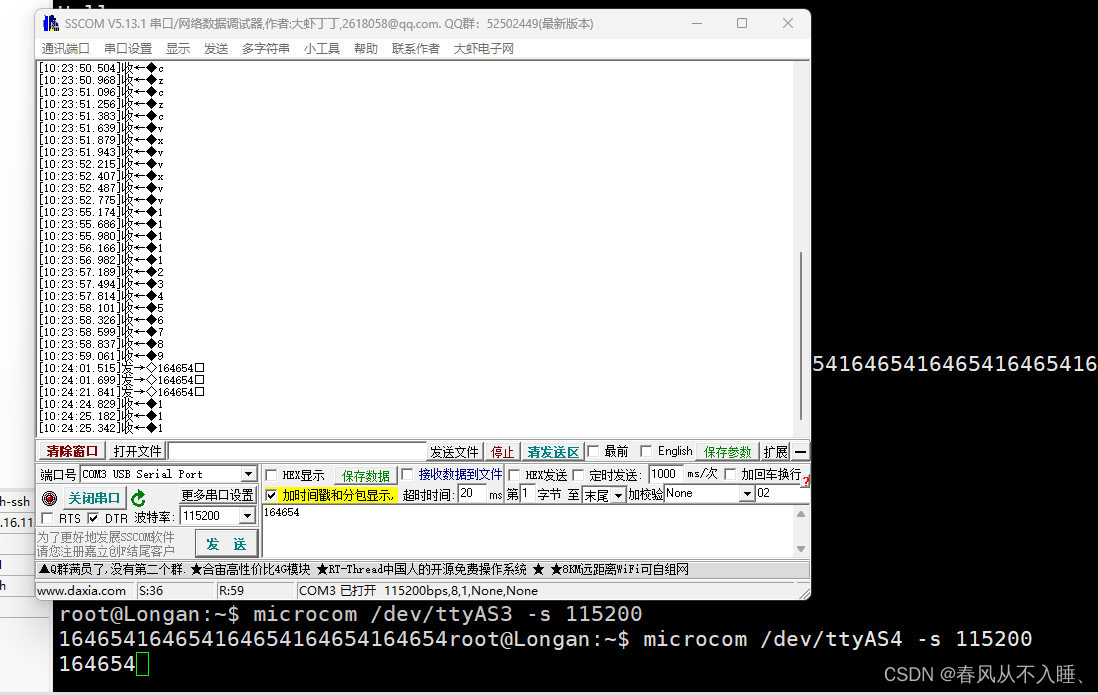
Linux RS232
一、确认硬件信息 RS232: 引脚信息: 二、软件配置 1、pinctrl信息: 2、设备树节点: 3、修改串口支持的模式 三、驱动 bsp/drivers/uart/sunxi-uart.c 四、烧录测试 查看串口参数: stty -F /dev/ttyAS3 -a stty -F…...
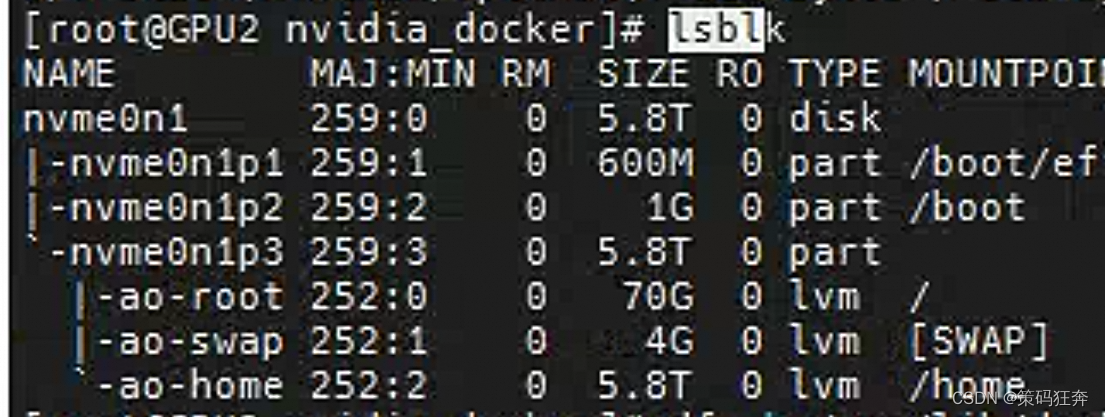
英伟达Docker 安装与GPu镜像拉取
获取nvidia_docker压缩包nvidia_docker.tgz将压缩包上传至服务器指定目录解压nvidia_docker.tgz压缩包 tar -zxvf 压缩包执行rpm安装命令: #查看指定rpm包安装情况 rpm -qa | grep libstdc #查看指定rpm包下的依赖包的版本情况 strings /lib64/libstdc |grep GLI…...

智慧交通的神经中枢:利用ARMxy进行实时交通流数据采集
气候变化和水资源日益紧张,精准农业成为了提高农业生产效率、节约资源的关键。在这一变革中,ARMxy工业计算机扮演了核心角色,特别是在智能灌溉系统的实施中。 背景介绍: 某大型农场面临着灌溉效率低、水资源浪费严重的问题。传统的…...

文心一言使用技巧
前言 文心一言是一款基于人工智能技术的自然语言处理工具,它可以帮助用户生成、编辑和优化各种类型的文本。无论是写作、翻译、总结,还是进行信息提取和数据分析,文心一言都能提供强大的支持。本文将详细介绍文心一言的使用技巧,…...

技术人如何打造研发团队
技术人作为写代码一路走上来,其实不像销售岗位,售后交付岗位与人的打交道那么多。主要是很简单的技术沟通,在慢慢走上管理岗位后,也是依据自己的经验,自己的感觉来管理团队,很多时候自己的事情不但没少&…...

月薪6万,想离职...
大家好,我是无界生长,国内最大AI付费社群“AI破局俱乐部”初创合伙人。这是我的第 39 篇原创文章——《月薪6万,想离职...》 是的,你没有看错,我月薪6万,却想离职,很不可思议吧?周围…...
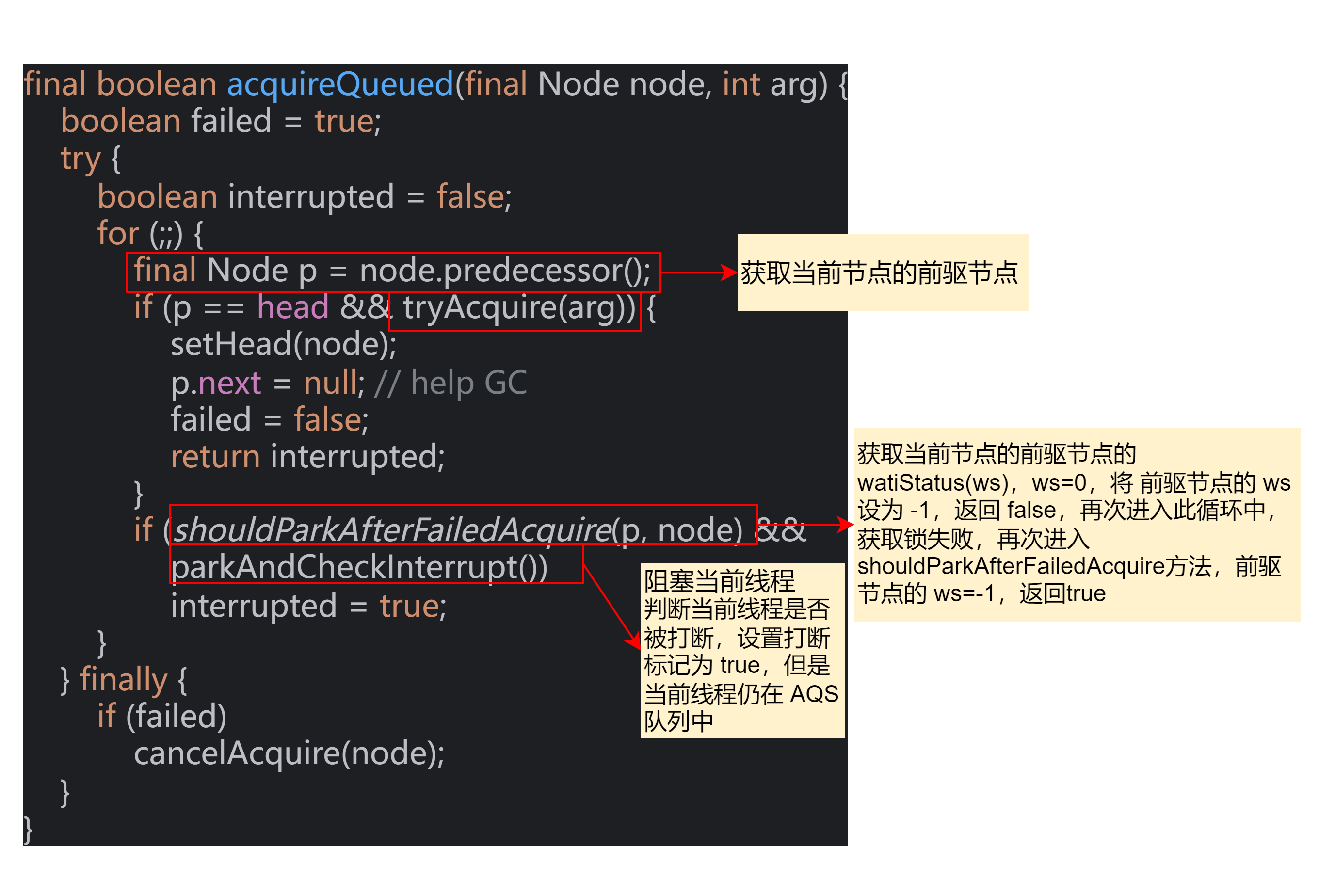
ReentrantLock底层原理
ReentrantLock public ReentrantLock() {sync new NonfairSync(); }public ReentrantLock(boolean fair) {sync fair ? new FairSync() : new NonfairSync(); }ReentrantLock 的默认实现是非公平锁,实际上 ReentrantLock 中的方法,几乎都让 sync 实现…...
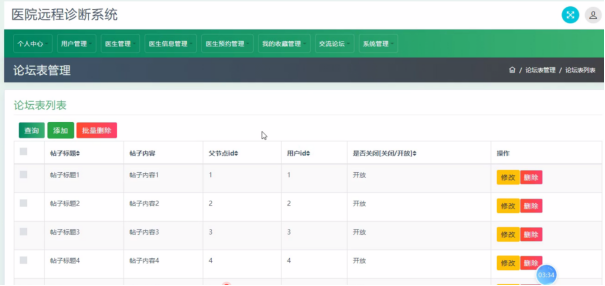
基于JSP的医院远程诊断系统
开头语: 你好呀,我是计算机学长猫哥!如果有相关需求,文末可以找到我的联系方式。 开发语言: Java 数据库: MySQL 技术: JSP Servlet JSPBean 工具: IDEA/Eclipse、Navica…...
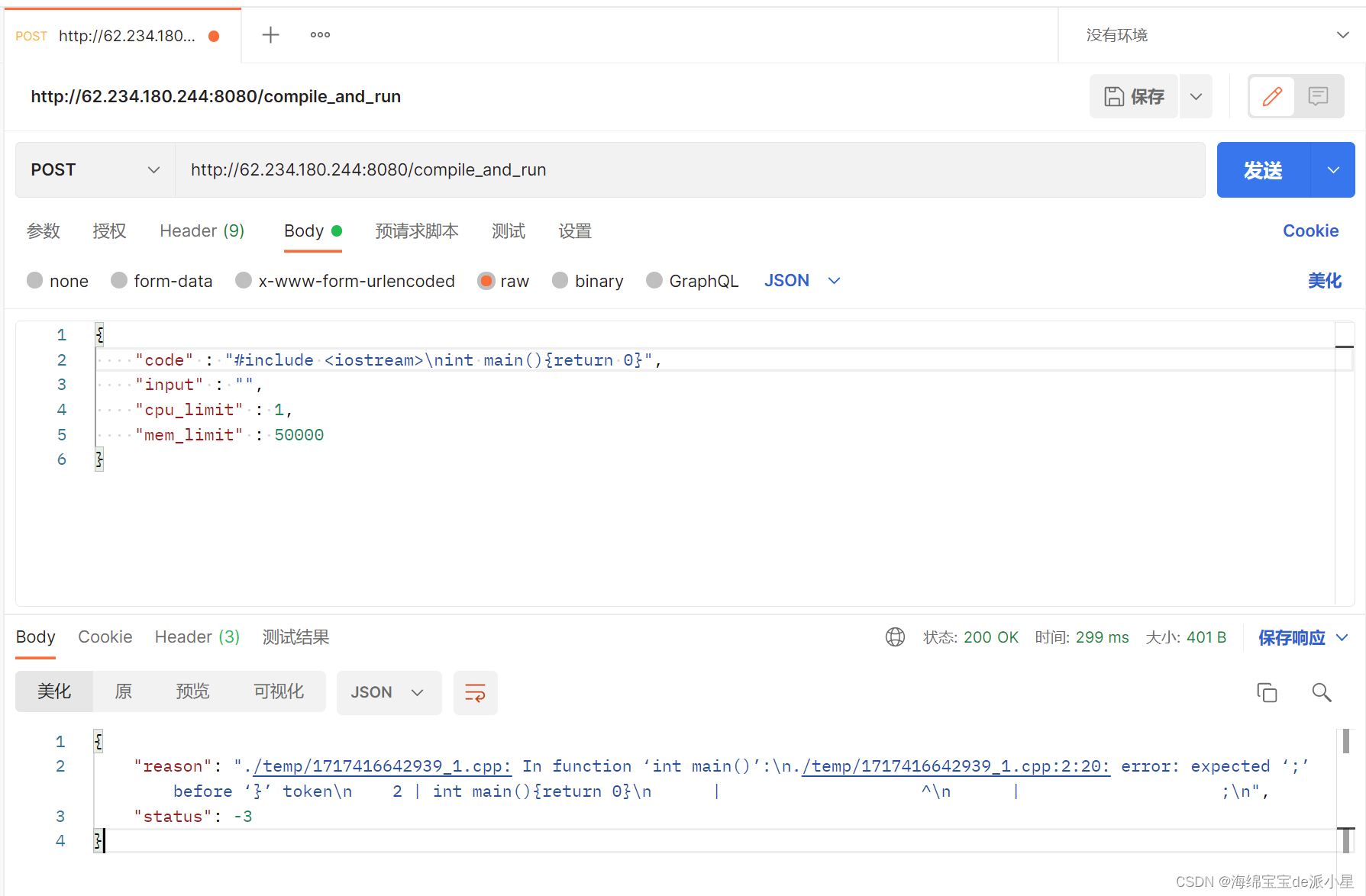
项目:基于httplib/消息队列负载均衡式在线OJ
文章目录 写在前面关于组件开源仓库和项目上线其他文档说明项目亮点 使用技术和环境项目宏观结构模块实现compiler模块runner模块compile_run模块compile_server模块 基于MVC结构的OJ服务什么是MVC?用户请求服务路由功能Model模块view模块Control模块 写在前面 关于…...

详解python中的pandas.read_csv()函数
😎 作者介绍:我是程序员洲洲,一个热爱写作的非著名程序员。CSDN全栈优质领域创作者、华为云博客社区云享专家、阿里云博客社区专家博主。 🤓 同时欢迎大家关注其他专栏,我将分享Web前后端开发、人工智能、机器学习、深…...

速盾:DDoS高防IP上设置转发规则
DDoS攻击是一种网络攻击方式,攻击者通过大量请求使目标服务器或网络资源超负荷运行,导致服务不可用。为了保护网络安全,减少DDoS攻击对网络的影响,使用DDoS高防IP可以是一种解决方案。而在DDoS高防IP上设置转发规则可以提高网络的…...
)
京东一面测开(KPI)
京东一面测开凉经(笔试ak) 3.8 面试官:你很优秀啊,你不用谦虚 没问技术相关,问了如何设计测试用例步骤一些理论: 什么是软件测试?其目的是什么? 软件测试有哪些类型?请列…...

Django框架中级
Django框架中级 – 潘登同学的WEB框架 文章目录 Django框架中级 -- 潘登同学的WEB框架 中间件自定义中间件常用中间件process_view() 使用中间件进行URL过滤 Django生命周期生命周期分析 Django日志日志配置filter过滤器自定义filter 日志格式化formatter Django信号内置信号定…...

cordova-plugin-inappbrowser内置浏览器插件
一、InAppBrowser(内置浏览器) 允许在在单独的窗口中加载网页。例如要向应用用户展示其他网页。当然可以很容易地在应用中加载网页内容并管理,但有时候需要不同的用户体验,InAppBrowser加载网页内容,应用用户可以更方便的直接返回到主应用。 二、安装命令: cordova pl…...

打造智慧工厂核心:ARMxy工业PC与Linux系统
智能制造正以前所未有的速度重塑全球工业格局,而位于这场革命核心的,正是那些能够精准响应复杂生产需求、高效驱动自动化流程的先进设备。钡铼技术ARMxy工业计算机,以其独特的设计哲学与卓越的技术性能,正成为众多现代化生产线背后…...

Java File IO
Java File IO ~主要介绍四个类 InputStream OutputStream FileReader FileWriter~ InputStream (字节流读取File) public static void main(String[] args) throws IOException {String filePath "D:\\Javaideaporject\\JavaBaseSolid8\\File\\t…...
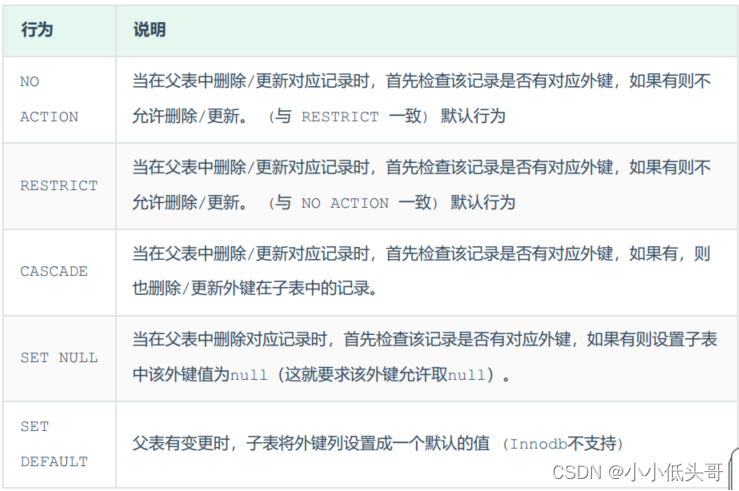
MySQL 函数与约束
MySQL 函数与约束 文章目录 MySQL 函数与约束1 函数1.1 字符串函数1.2 数值函数1.3 日期函数1.4 流程函数 2 约束2.1 概述2.2 约束演示2.3 外键约束2.4 删除/更新行为 1 函数 函数是指一段可以直接被另一程序调用的程序或代码。 1.1 字符串函数 MySQL中内置了很多字符串函数&…...

12_1 Linux Yum进阶与DNS服务
12_1 Linux Yum进阶与DNS服务 文章目录 12_1 Linux Yum进阶与DNS服务[toc]1. Yum进阶1.1 自定义yum仓库1.2 网络Yum仓库 2. DNS服务2.1 为什么要使用DNS系统2.2 DNS服务器的功能2.3 DNS服务器分类2.4 DNS服务使用的软件及配置2.5 搭建DNS服务示例2.6 DNS特殊解析 1. Yum进阶 1…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
