C++经典150题
经典150题
数组/字符串
文章目录
- 经典150题
- 数组/字符串
- 88. 合并两个有序数组
- 27.移除元素
- 26.删除有序数组中的重复项
- 80.删除有序数组重点重复项II
- 169.多数元素
- 189.轮转数组
- 121.买卖股票的最佳时机
- 123.买卖股票的最佳时机 III
- 55.跳跃游戏
- 45.跳跃游戏II
88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
解法1:先合并后排序
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {for (int i = 0; i<n ; i++){nums1[m+i] = nums2[i];}sort(nums1.begin(),nums1.end());}
};
时间复杂度为 O((m+n)log(m+n)) (快速排序–对数级时间复杂度)
空间复杂度为 O(log(m+n)) (快速排序–对数级空间复杂度)
解法2:双指针
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {vector<int> result;int p1 = 0, p2 = 0;int cur;while ( p1<m || p2<n ){if (p1==m){cur = nums2[p2++];}else if (p2 == n){cur = nums1[p1++];}else if (nums1[p1] <= nums2[p2]){cur = nums1[p1++];}else{cur = nums2[p2++];}result.push_back(cur);}for (int i = 0; i<m+n; i++){nums1[i] = result[i];}}
};
时间复杂度为O(m+n)
空间复杂度为O(m+n)
解法3:==逆向双指针(==从后向前遍历)
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {int p1=m-1,p2=n-1;int index = m+n-1;while (p1>=0 || p2>=0){if (p1 ==-1){nums1[index--] = nums2[p2--];}else if (p2 == -1){nums1[index--] = nums1[p1--];}else if (nums1[p1]<=nums2[p2]){nums1[index--] = nums2[p2--];}else{nums1[index--] = nums1[p1--];}}}
};
时间复杂度为O(m+n)
空间复杂度为O(1)
27.移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
class Solution {
public:int removeElement(vector<int>& nums, int val) {int slow = 0;for(int fast = 0 ; fast < nums.size() ; fast++ ){if(nums[fast] != val){nums[slow] = nums[fast];slow++;}}return slow;}
};
时间复杂度O(n)
空间复杂度O(1)
26.删除有序数组中的重复项
给你一个 非严格递增排列 的数组 nums ,请你** 原地** 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
- 更改数组
nums,使nums的前k个元素包含唯一元素,并按照它们最初在nums中出现的顺序排列。nums的其余元素与nums的大小不重要。 - 返回
k。
class Solution {
public:int removeDuplicates(vector<int>& nums) {if (nums.size()==0){return 0;}int slow=1, fast =1;for (;fast<nums.size();fast++){if (nums[fast]!=nums[fast-1]){nums[slow++] = nums[fast];}}return slow;}
};
时间复杂度:O(n)
空间复杂度:O(1)
80.删除有序数组重点重复项II
给你一个有序数组 nums ,请你** 原地** 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
class Solution {
public:int removeDuplicates(vector<int>& nums) {if (nums.size()<=2){return nums.size();}int slow = 2,fast = 2;for (;fast<nums.size();fast++){if (nums[slow-2]!=nums[fast]){nums[slow++] = nums[fast];}}return slow;}
};
//拓展:将原问题的【保留2位】改为【保留k位】,则判断条件为 nums[slow-k]!=nums[fast]
时间复杂度O(n)
空间复杂度O(1)
169.多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
解法1:哈希表
class Solution {
public:int majorityElement(vector<int>& nums) {unordered_map<int, int> counts;int majority = 0, cnt = 0;for (int num: nums) {counts[num]++;if (counts[num] > cnt) {majority = num;cnt = counts[num];}}return majority;}
};时间复杂度O(n)
空间复杂度O(1)
解法2:排序,中间的数一定是多数元素
class Solution {
public:int majorityElement(vector<int>& nums) {sort(nums.begin(),nums.end());return nums[nums.size()/2];}
};
时间复杂度O(nlogn)
空间复杂度O(logn)
其他方法:随机化、分治、Boyer - Moore投票算法
189.轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
解法1:数组翻转
class Solution {
public:void rotate(vector<int>& nums, int k) {k%=nums.size();reverseList(nums,0,nums.size());reverseList(nums,0,k);reverseList(nums,k,nums.size());}void reverseList(vector<int>& nums, int start, int end){reverse(nums.begin()+start,nums.begin()+end);}
};
时间复杂度O(n)
空间复杂度O(1)
121.买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
class Solution {
public:int maxProfit(vector<int>& prices) {int inf = 1e9;int minprice = inf;int maxprofit = 0;for (int price:prices){minprice = min(minprice,price);maxprofit = max(maxprofit,price-minprice);}return maxprofit;}//数组开始递减的时候会找最小值,只有开始递增的时候计算差值
};
时间复杂度O(n)
空间复杂度O(1)
123.买卖股票的最佳时机 III
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润
class Solution {
public:int maxProfit(vector<int>& prices) {int profit = 0;for (int i =1; i<prices.size(); i++){if (prices[i]>prices[i-1]){profit+=prices[i]-prices[i-1];}}return profit;}//贪心算法
};
时间复杂度O(n)
空间复杂度O(1)
55.跳跃游戏
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
解法1:遍历数组,判断能到达的最远距离
class Solution {
public:bool canJump(vector<int>& nums) {int reach = 0;for (int i = 0; i<nums.size(); i++){if (i>reach){return false;}reach = max(reach, i+nums[i]);}return true;}
};
时间复杂度O(n)
空间复杂度O(1)
解法2:找从早从哪里出发
class Solution {
public:bool canJump(vector<int>& nums) {int last= nums.size()-1;for (int i = nums.size()-2; i>=0; i--){if (nums[i]+i>=last){last = i;}return last==0;}}
};
时间复杂度O(n)
空间复杂度O(1)
45.跳跃游戏II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
class Solution {
public:int jump(vector<int>& nums) {int maxPos=0, end=0;int step = 0;for (int i=0;i<nums.size()-1;i++){maxPos = max(nums[i]+i,maxPos);if (i==end){end = maxPos;step++;}}return step;}
};
时间复杂度O(n)
空间复杂度O(1)
相关文章:

C++经典150题
经典150题 数组/字符串 文章目录 经典150题数组/字符串88. 合并两个有序数组27.移除元素26.删除有序数组中的重复项80.删除有序数组重点重复项II169.多数元素189.轮转数组121.买卖股票的最佳时机123.买卖股票的最佳时机 III55.跳跃游戏45.跳跃游戏II 88. 合并两个有序数组 给…...

超详解——Python 序列详解——基础篇
目录 1. 序列的概念 字符串(String) 列表(List) 元组(Tuple) 2. 标准类型操作符 连接操作符() 重复操作符(*) 索引操作符([]) …...

DVWA-DC-6
靶机IP:192.168.20.140 kaliIP:192.168.20.128 网络有问题的可以看下搭建Vulnhub靶机网络问题(获取不到IP) 信息收集 nmap扫描靶机端口及版本信息 dirsearch扫目录 发现是个wordpress建站 我们去访问前端界面 存在重定向,修改hosts文件,加入192.168…...

ubuntu早期版本以及18.04后的版本,通过rc.local配置开机自启
在ubuntu早期版本以及18.04后的版本,还是支持在rc.local中进行操作开机自启。 1、编辑rc.local文件 cat <<EOF >/etc/rc.local #!/bin/sh -e # rc.local # This script is executed at the end of each multiuser runlevel. # Make sure that the script…...

【环境搭建】1.阿里云ECS服务器 安装jdk8
在阿里云服务器上安装 JDK 8 可以通过以下步骤完成。假设你使用的是 CentOS 或者其他基于 Red Hat 的发行版或Alibaba Cloud Linux 3.2104 LTS 64位。 1.更新系统软件包 sudo yum update -y2.安装 OpenJDK 8 使用 yum 包管理器安装 OpenJDK 8 sudo yum install -y java-1.8…...
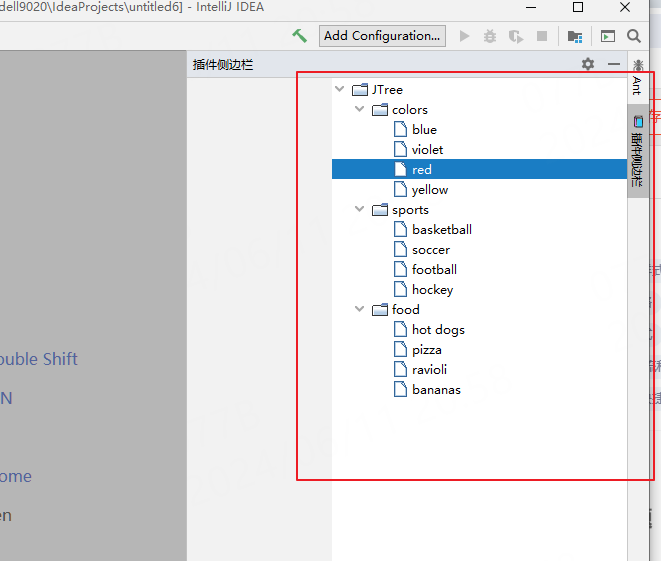
idea插件开发之定义侧边栏
写在前面 看下如何在侧边栏定义窗口,如下的效果: 1:正戏 先来定义UI,随便拖拽个组件,就看个效果: 接着定义一个工厂类来创建这个UI,需要实现接口com.intellij.openapi.wm.ToolWindowFactor…...

HarmonyOS未来五年的市场展望
一、引言 随着科技的不断进步和消费者对于智能化设备需求的日益增长,操作系统作为连接硬件与软件的核心平台,其重要性愈发凸显。HarmonyOS(鸿蒙系统),作为华为自主研发的分布式操作系统,自诞生以来便备受瞩…...
?)
R语言:什么是向量化操作(Vectorization)?
在R语言中,向量化操作是一个非常重要且强大的概念。它不仅提高了代码的简洁性和可读性,还大大提升了代码的执行效率。本文将详细介绍什么是向量化操作,并通过几个示例来展示其应用。 什么是向量化操作? 向量化操作是指在不使用显…...

Python 机器学习 基础 之 【实战案例】中药数据分析项目实战
Python 机器学习 基础 之 【实战案例】中药数据分析项目实战 目录 Python 机器学习 基础 之 【实战案例】中药数据分析项目实战 一、简单介绍 二、中药数据分析项目实战 三、数据处理与分析实战 1、数据读取 2、中药材数据集的数据处理与分析 2.1数据清洗 2.2、 提取别…...

python中报错“ModuleNotFoundError: No module named ‘docx2txt‘”
python中from langchain_community.document_loaders import Docx2txtLoader报错“ModuleNotFoundError: No module named ‘docx2txt’” 问题描述: python中from langchain_community.document_loaders import Docx2txtLoader报错“ModuleNotFoundError: No module named ‘…...

json.dumps参数
json.dumps()是 Python 中json 模块的一个函数,用于将 Python 对象编码成 JSON格式的字符串。这个函数有几个常用的参数,下面是一些主要的参数及其描述: 1. **obj**: 必需。要转换的 Python 对象。 2. *…...

未来已来,划时代革命性产品——全息数字人管家系统,全网首发
尊敬的投资人、亲爱的网友们: 大家好,我是数字人管家项目总设计师,我叫William wang。在这个科技日新月异的时代,我们正站在一个前所未有的交汇点上,数字与现实的边界日益模糊,智能技术正以前所未有的方式…...

psql导入数据报错排查
问题:采用pg_dump导出表数据后,用psql导入表数据,导入时报错 无效的命令 \N定位该问题的方法 --进入psql \set ON_ERROR_STOP on --退出psqlpsql -U postgres -d test -v ON_ERROR_STOPon < /home/postgres/test.dmp参考文章:…...
项目:双人五子棋对战-对战模块(6)
完整代码见: 邹锦辉个人所有代码: 测试仓库 - Gitee.com 当玩家进入到游戏房间后, 就要开始一局紧张而又刺激的五子棋对战了, 本文将就前端后端的落子与判断胜负的部分作详细讲解. 模块详细讲解 约定前后端交互的接口 首先是建立连接后, 服务器需要生成一些游戏的初始信息(可…...
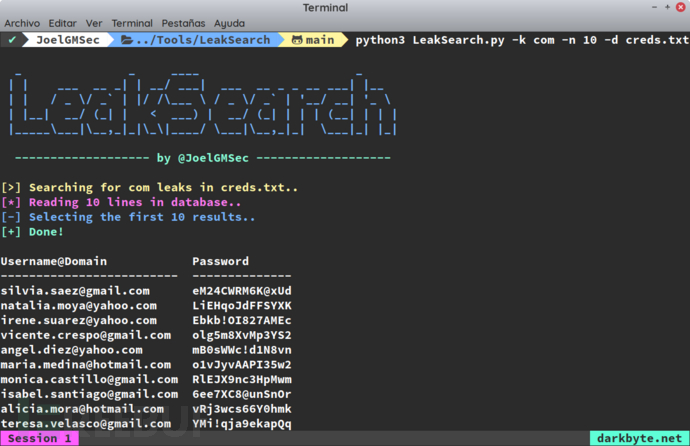
LeakSearch:针对网络公开凭证的安全扫描与检测工具
关于LeakSearch 在红队演戏过程中,往往需要获取到针对目标域的访问权限。在这个过程中,很多红队人员会选择使用暴露在互联网上的代理服务器来实现目标域的访问,那么此时就需要在互联网上收集公开暴露的凭证信息。 对于蓝队来说,…...
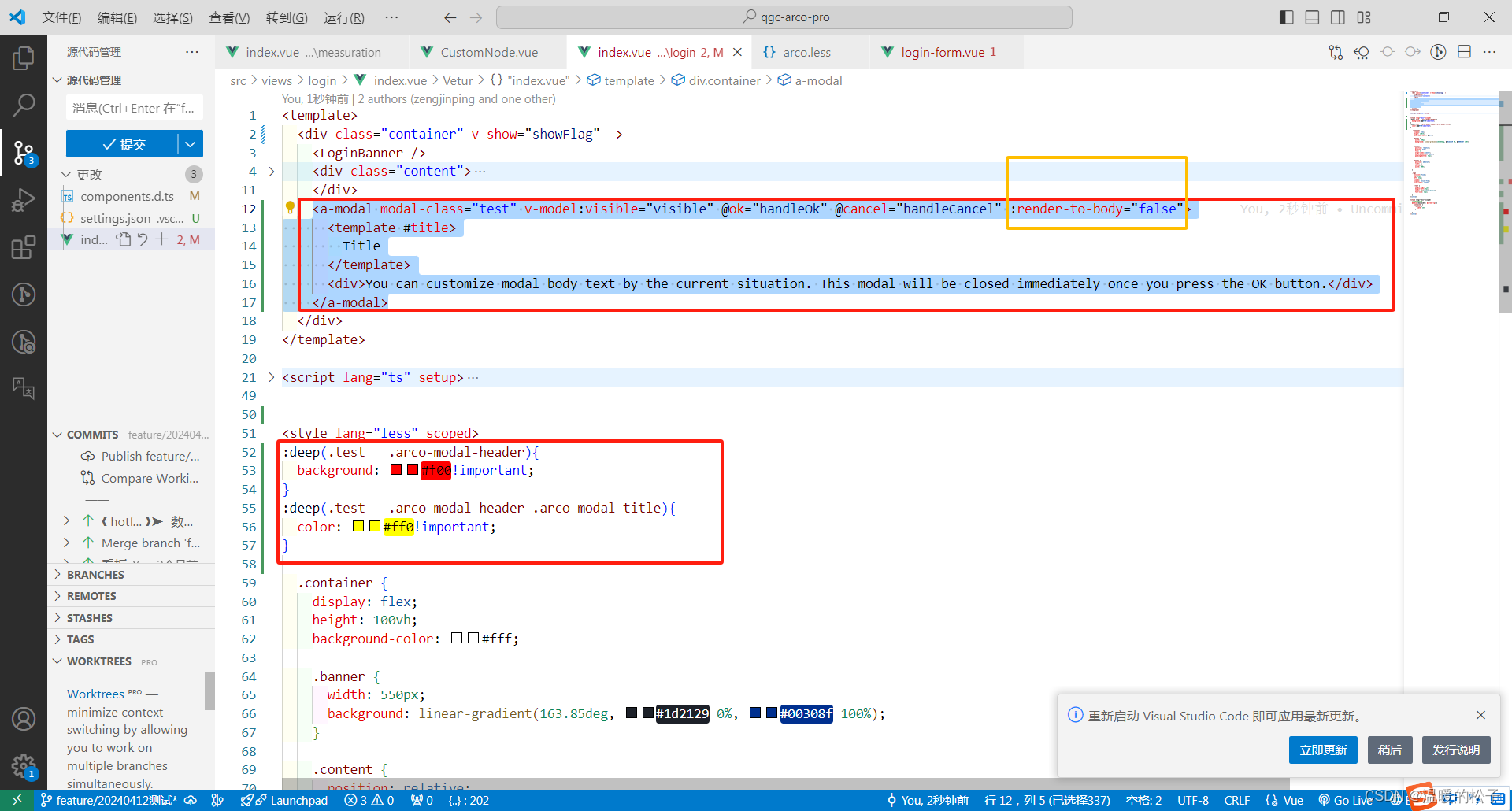
ArcoDesgin a-model中自定义样式model-class无效
增加黄框代码解决 原因是,动态加载的组件默认渲染在body下面,与#app平级。样式设置无效 加上:render-to-body“false”,让组件不渲染到body下,渲染在app下面,样式设置生效...
)
持续总结中!2024年面试必问 20 道分布式、微服务面试题(十)
上一篇地址:持续总结中!2024年面试必问 20 道分布式、微服务面试题(九)-CSDN博客 十九、请描述一种微服务部署策略。 微服务部署策略是确保微服务架构中各个独立服务能够高效、稳定地部署到生产环境中的方法。以下是一些常见的微…...
北航第四次数据结构与程序设计编程题复习
到期末了,所以再来复习一下以前的作业。 北航第四次数据结构与程序设计编程题 一、栈操作(栈-基本题)二、C程序括号匹配检查三、计算器(表达式计算-后缀表达式实现,结果为浮点)四、文本编辑操作模拟&#…...

golang调用外部程序包os/exec中的 Command和CommandContext 函数创建的Cmd对象的区别
在go语言中,我们可以通过os/exec包中的Command和CommandContext 函数创建对应的外部程序执行Cmd对象, 这2个函数创建的cmd命令执行对象是有区别的,CommandContext创建的对象可以携带上下文,这个主要用于我们通过cancel函数给对应的…...
Redis进阶知识个人汇总
持久化 三种方式实现它的持久化: RDB持久化 全称Redis数据备份文件,又称Redis数据快照 这种就是将Redis内存中所有数据记录到磁盘中,当实例出故障后,从磁盘中读快照文件进行恢复数据。 一般使用bgsave指令实现 复制主线程得到一…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
