数据结构习题(快期末了)
一个数据结构是由一个逻辑结构和这个逻辑结构上的一个基本运算集构成的整体。
从逻辑关系上讲,数据结构主要分为线性结构和非线性结构两类。
数据的存储结构是数据的逻辑结构的存储映像。
数据的物理结构是指数据在计算机内实际的存储形式。
算法是对解题方法和步骤的描述。
若一个算法中的语句频度之和为T(n)=6n+3nlog2n,则算法的时间复杂度为 O(nlog2n)
若一个算法中的语句频度之和为T(n)=3n+nlog2n+n2,则算法的时间复杂度为O(n2)
一个算法的时间复杂性是算法 输入规模 的函数。
算法的空间复杂度是指该算法所耗费的存储空间,它是该算法求解问题规模n的函数。
数据有逻辑结构和 (物理结构 )两种结构。
数据逻辑结构除了集合以外,还包括:线性结构、树形结构和( 图形结构 )
数据结构按逻辑结构可分为两大类,它们是线性结构和(非线性结构 )
在树形结构中,除了树根结点以外,其余每个结点只有(一 )个前驱结点。
在图形结构中,每个结点的前趋结点数和后续结点数可以有(多 )个。
数据的存储结构又叫(物理结构 )
数据的存储结构形式包括:顺序存储、链式存储、索引存储和( 哈希存储 )
线性结构中的元素之间存在( 一对一 )的关系。
树形结构结构中的元素之间存在( 一对多 )的关系。
数据结构主要研究数据的逻辑结构、存储结构和(算法 )三个方面的内容。
数据在计算机存储器内表示时,物理地址和逻辑地址相同并且是连续的,称之为( 顺序存储结构 )
链式存储的存储结构所占存储空间(分两部分,一部分存放结点的值,另一部分存放表示结点间关系的指针 )
算法的计算量大小称为算法的时间复杂性
每个结点只含有一个数据元素,所有存储结点相继存放在一个连续的存储区里,这种存储结构称为顺序结构
算法分析的两个主要方面是空间复杂性和时间复杂性
数据结构是一门研究在非数值计算的程序设计问题中所涉及的( 数据元素)以及它们之间的关系和运算的科学。
在Data_Structure=(D,R)中,D是(数据元素 )的有限集合。
线性结构中结点形成一对一的关系
树形结构具有分支和层次的特点,其形态有些像自然界中的树
图形结构中的元素按其逻辑关系互相连接,每个结点都可能与其他结点邻接
从逻辑上可将数据结构分为线性结构和非线性结构
在存储数据时,通常不仅需要存储数据元素的值,还要存储数据元素之间的关系
线性结构的特点是元素之间的关系是( 一对一)的关系。
数据的基本单位是数据元素。
在数据结构中,与所使用的计算机无关的是(逻辑结构 )
数据元素之间关系最弱的是( 集合)



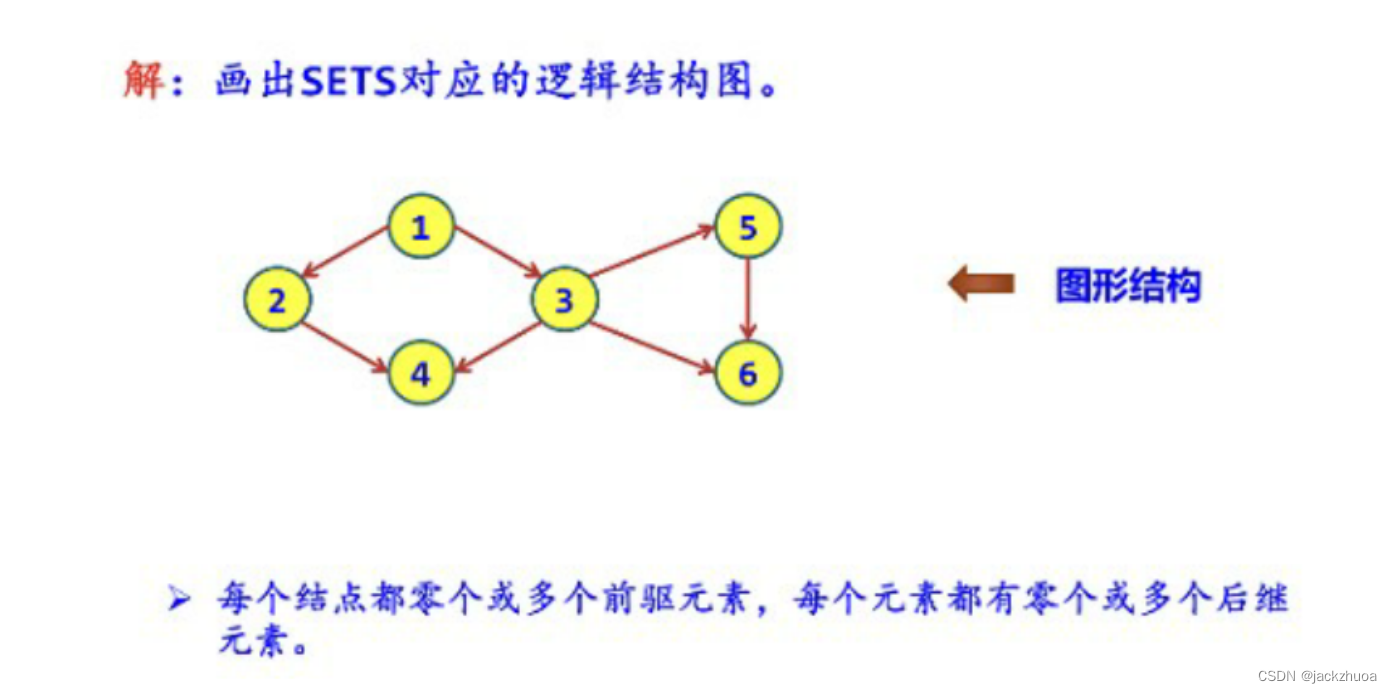
数据在计算机存储器内表示时,物理地址和逻辑地址相同并且是连续的,称之为 顺序存储结构 。
设a、b、c为三个结点,p、10、20分别代表它们的地址,则如下的存储结构称为 单链表。
![]()
用链表存储的线性表,其优点是 便于插入和删除 。
线性表采用链式存储时,结点的存储地址连续与否均可 。
线性表采用顺序存储必须占用一片连续的存储空间
线性表采用链式存储不必占用一片连续的存储空间
线性表采用链式结构便于插入和删除的操作
在一个单链表中,若q所指结点是p所指结点的前驱结点,若在q与p之间插入一个s所指的结点,则执行 s→next=p; q→next=s; 。
如果线性表中的表元素既没有直接前驱,也没有直接后继,则该线性表中应有(1 )个表元素。
在长度为n的顺序表的表尾插入一个新元素的时间复杂度为( O(1))。
顺序表的优点是存储密度高,但插入与删除运算的时间效率低
设一个顺序表中有n个元素,则读取第i个数组元素的平均时间复杂度为O(1)
在一个长度为n的顺序存储线性表中,向第i个元素(1....i....n)之前插入一个新元素时,需要从后向前依次后移(n-i+1)个元素。
设一条单链表的头指针变量为head且该链表没有头节点,则其判空条件是(Head = = 0)
线性结构中的元素之间存在( 一对一 )的关系。
在线性表的顺序存储中,若一个元素的下标为i,则它的前驱元素的下标为(i-1 ),后继元素的下标为(i+1 )
当线性表的数据元素在物理位置上是连续存储的时候,用(顺序表 )比用链表好,其特点是可以进行随机存取。
在线性表的单链接存储结构中,若一个元素所在结点的地址为p,则其后继结点的地址为( p->next )。
在线性表的单链接存储结构中,每个结点包含有两个域,一个叫(数据 )域,另一个叫( 指针 )域。
栈和队列
假设一个栈的输入序列是1,2,3,4,则不可能得到的输出序列是4,1,2,3

其中4,3,2,1可以,1,3,2,4可以,1,2,3,4,也可以
已知一个栈的进栈序列为1,2,.....,n,其输出序列是p1,p2,...pn。若p1=3,则p2的值可能是2

当利用大小为n的数组顺序存储一个栈时,假定用top==n表示栈空,则向这个栈插入一个元素时,首先应执行(top - -)语句修改top指针
如果进栈元素依次为13,20,15,43,38,65,47,现退出4个元素,再插入1个元素,则43的位置是不在栈内
栈和队列的共同特点是(只允许在端点处插入和删除元素 )。
若进队的序列为:A,B,C,D,则出队的序列是(A,B,C,D )。

栈的插入和删除操作在(栈顶 )进行。
设数组data[m]作为循环队列SQ的存储空间,front为队头指针,rear为队尾指针,则执行出队操作后其头指针front值为(front=(front+1)%(m+1))。

链栈与顺序栈相比,有一个比较明显的优点是通常不会出现栈满的情况
插入和删除只能在一端进行的线性表,称为(栈 )。
队列通常采用两种存储结构是顺序存储结构和链式存储结构
个队列的入队顺序是1,2,3,4,5,则队列的输出顺序是( 1,2,3,4,5)
先进先出
顺序存储的循环队列sq中,假定front和rear分别为队头指针和队尾指针,则入队操作为(sq.rear=(sq.rear+1)%maxsize;sq.data[sq.rear]=x;)。
顺序存储的循环队列sq中,假定front和rear分别为队头指针和队尾指针,则出队操作为(sq.front=(sq.front+1)%maxsize)。

在具有m个单元的顺序存储的循环队列中,假定front和rear分别为队头指针和队尾指针,则判断队满的条件为(D.(rear+1) % m==front )。
在具有m个单元的顺序存储的循环队列中,假定front和rear分别为队头指针和队尾指针,则判断队空的条件为(rear = = front )。
设顺序循环队列Q[0:M-1]的头指针和尾指针分别为F和R,头指针F总是指向队头元素的前一位置,尾指针R总是指向队尾元素的当前位置,则该循环队列中的元素个数为((R-F+M)%M )。
在一个顺序循环队列中,队头指针指向队头元素的(前一个 )位置。
顺序存储的循环队列sq中,假定front和rear分别为队头指针和队尾指针,则读队头元素时所执行的操作为(x=sq.data[(sq.front+1)%maxsize] )。
链栈与顺序栈相比,有一个比较明显的优点,即(通常不会出现栈满的现象)
用链接方式存储的队列,在进行删除运算时(头、尾指针可能都要修改)
用单链表表示的链队列的队头在链表的( 链头 )位置。
一个链队列q的队头和队尾指针是front和rear,该链队列已经存储有3个元素,现在有结点P要入队,入队操作是(q->rear->next=p; q->rear=p;)。
个链队列q的队头和队尾指针是front和rear,该链队列已经存储有3个元素,指针t 指向队头结点。如果做出队操作,出队结点的值要赋值给e, 出队操作是(q->front=q->front->next; e=t->data; free(t);)。
已知表达式,求它的后缀表达式是( 栈 )的典型应用。
一个栈的输入序列是abcde,则栈的输出序列dceab(不可能 )(填可能/不可能)
最后不可能时ab
栈可以看成是一种运算受限制的线性表,其中可以进行插入和删除的一端称为(栈顶 )
往栈中插入元素的操作方式是(入栈 )
删除栈中的元素的操作方式是( 出栈 )
当栈中的最大长度难以估计时,栈最好采用(链式 )存储结构
栈结构通常采用的两种存储结构是(顺序栈 )和( 链栈)
( 栈 )可作为实现递归函数调用的一种数据结构。
什么是队列的上溢现象和假溢出现象,解决它们有什么方法

二叉树的第k层的结点数最多为2k-1
对任意一棵树,设它有n个结点,这n个结点的度数之和为n-1 。
结点的总数目=所有结点度数之和+1;
既然是一颗树,那么总的节点数=总的边数+1
在一棵度为3的树中,度为3的结点个数为2,度为2 的结点个数为1,则度为0的结点个数为6 。
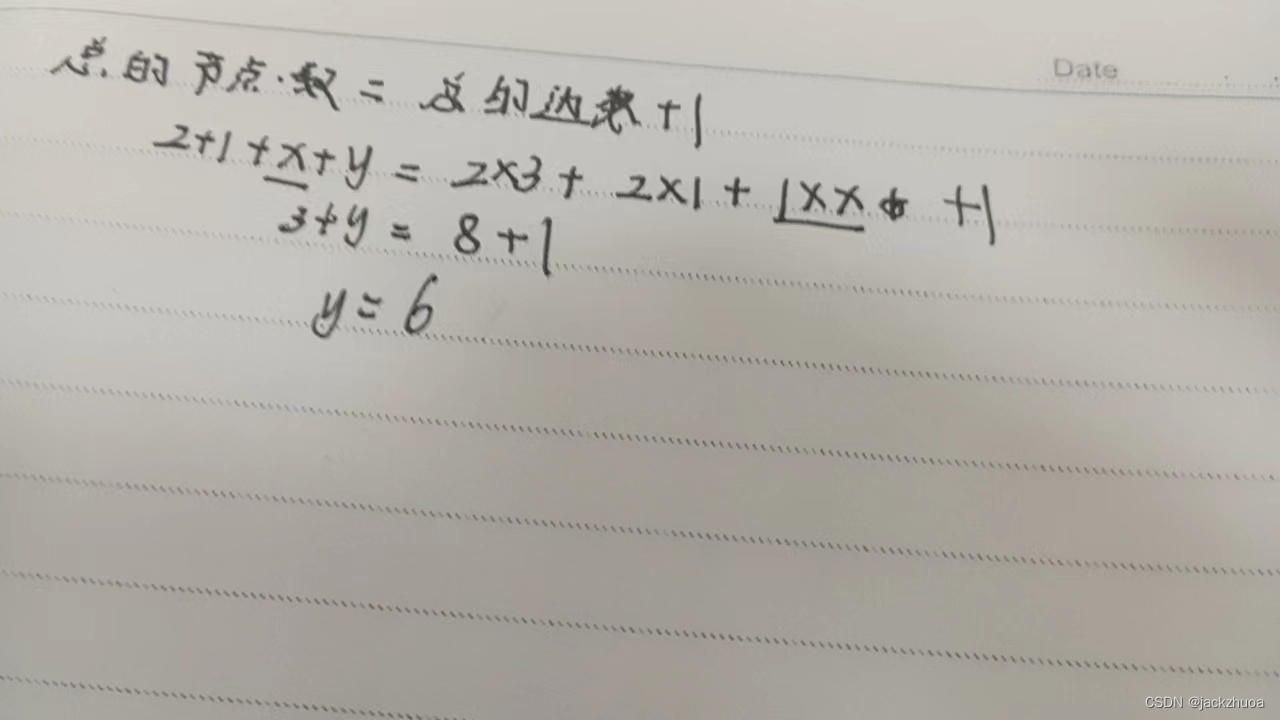
二叉树中第i(i≥1)层上的结点数最多有2i-1 个。
设结点A有3个兄弟结点且结点B为结点A的双亲结点,则结点B的度数数为4
(度数好像就是有几个子节点)
权值分别为11,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为71 。
二叉树的先序遍历序列中,任意一个结点均处在其孩子结点的前面,这种说法( )。正确
(根左右,肯定后面是孩子节点啊)
设高度为h的二叉树上只有度为0和度为2的结点,则此类二叉树中所包含的结点数最多为( )。

由于二叉树中每个结点的度最大为2,所以二叉树是一种特殊的树,这种说法( 正确)。
假定在一棵二叉树中,双分支结点数为15,单分支结点数为30,则叶子结点数为(16 )个。
在二叉树中:n0=n2+1。n0为出度为0的结点数,n2为度为2的结点数。因为双分支结点数为15个,所以叶子结点数为n0=n2+1=15+1=16个。
某二叉树的先序遍历序列是abdgcefh,中序遍历序列是dgbaechf,则其后序遍历序列是( )。
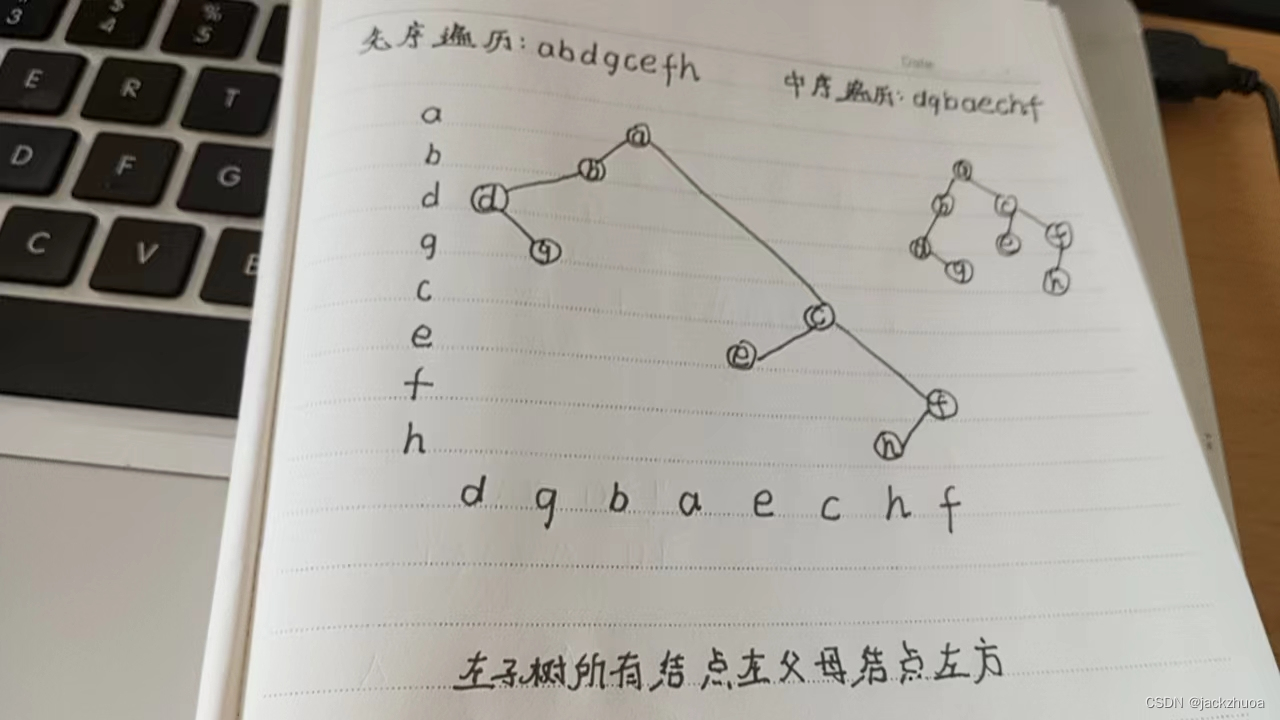
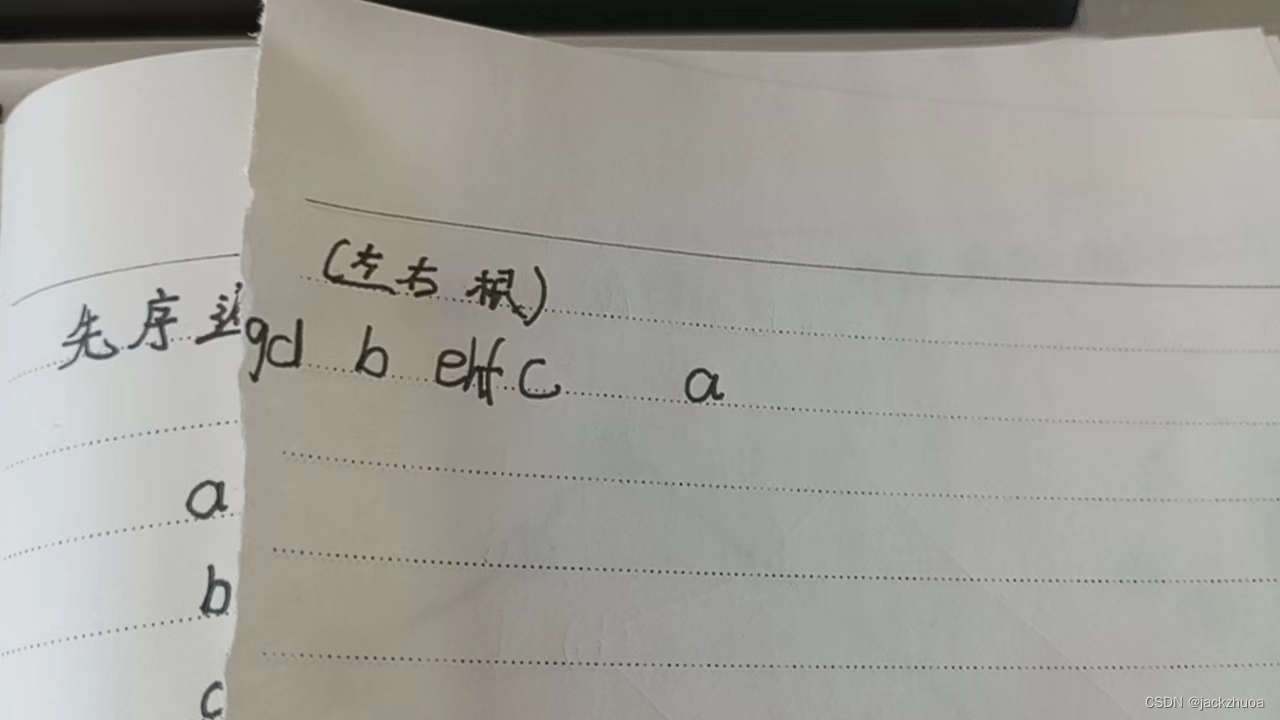
设树T的度为4,其中度为1,2,3和4的结点个数分别为4,2,1,1 则T中的叶子数为(8 ) 。
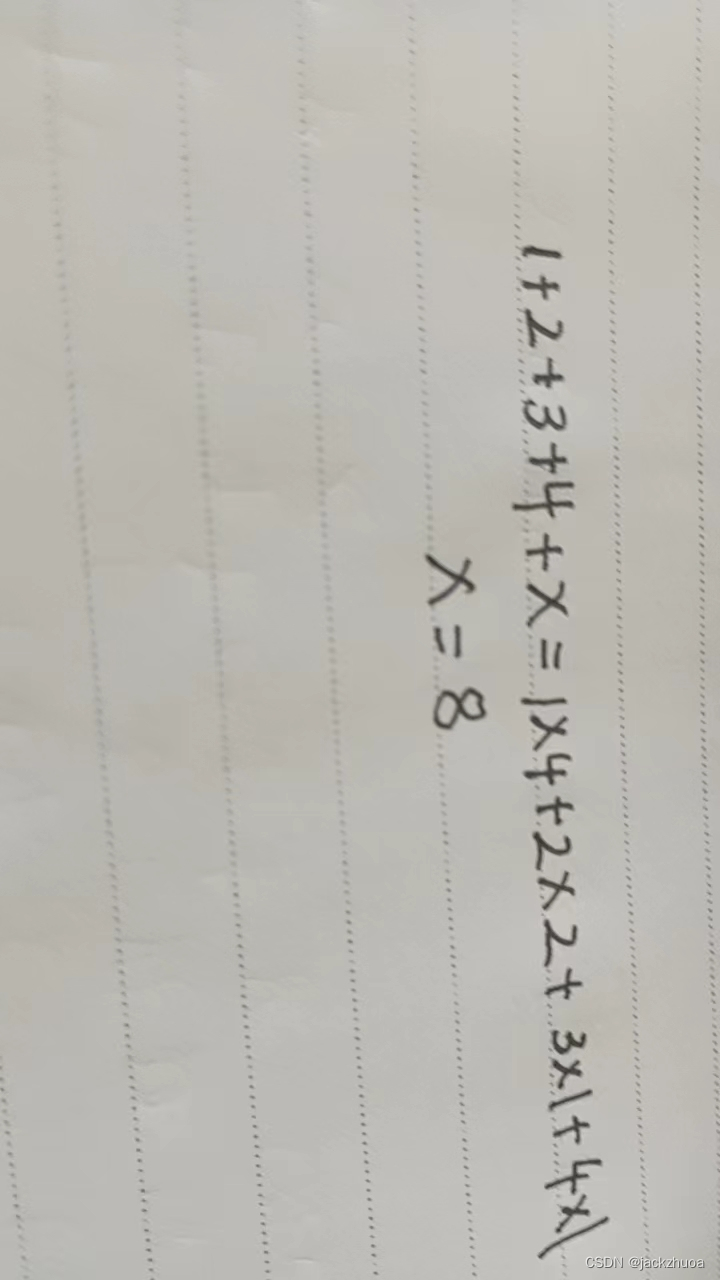
若一棵二叉树具有10个度为2的结点,5个度为1的结点,则度为0的结点个数是(11 )。
10+1=11
具有10个叶结点的二叉树中有(9 )个度为2的结点,。
10-1=9
一棵完全二叉树上有1001个结点,其中叶子结点的个数是(501 )
对于完全二叉树来说,n为偶数,叶子节点的个数为n/2,如果n为奇数,叶子节点的个数为n/2+1
二叉树中度为0的叶子结点个数为n0,度为1结点个数为n1,度为2结点个数为n2,于是n0 + n1 + n2 = 1001 根据二叉树性质:n0 = n 2 + 1,代入得到,2n2 + 1+ n1 = 1001 由于完全二叉树的n1 只能是0或者1,为满足2n2 + 1 + n1 = 1001,n1 =0,因此n2 = 500 所以n0 = 501,即叶子个数是501个
设给定权值总数有n 个,其哈夫曼树的结点总数为(2n_1 )。
哈夫曼树中权值所在的节点一定是叶子节点,有哈夫曼树的构造决定的。 因此“给定权值总数有n个”,也就是说叶子节点有n个,则度为2的节点个数为(n-1),哈夫曼树总结点个数为n+ (n-1)=2n-1
有关二叉树下列说法正确的是(一棵二叉树的度可以小于2 )。
二叉树的第I层上最多含有结点数为( ![]() ) 。
) 。
一棵二叉树高度为h,所有结点的度或为0,或为2,则这棵二叉树最多有(2 的h-1 )结点。
对于有n 个结点的完全二叉树, 其高度为( ![]() +1)
+1)
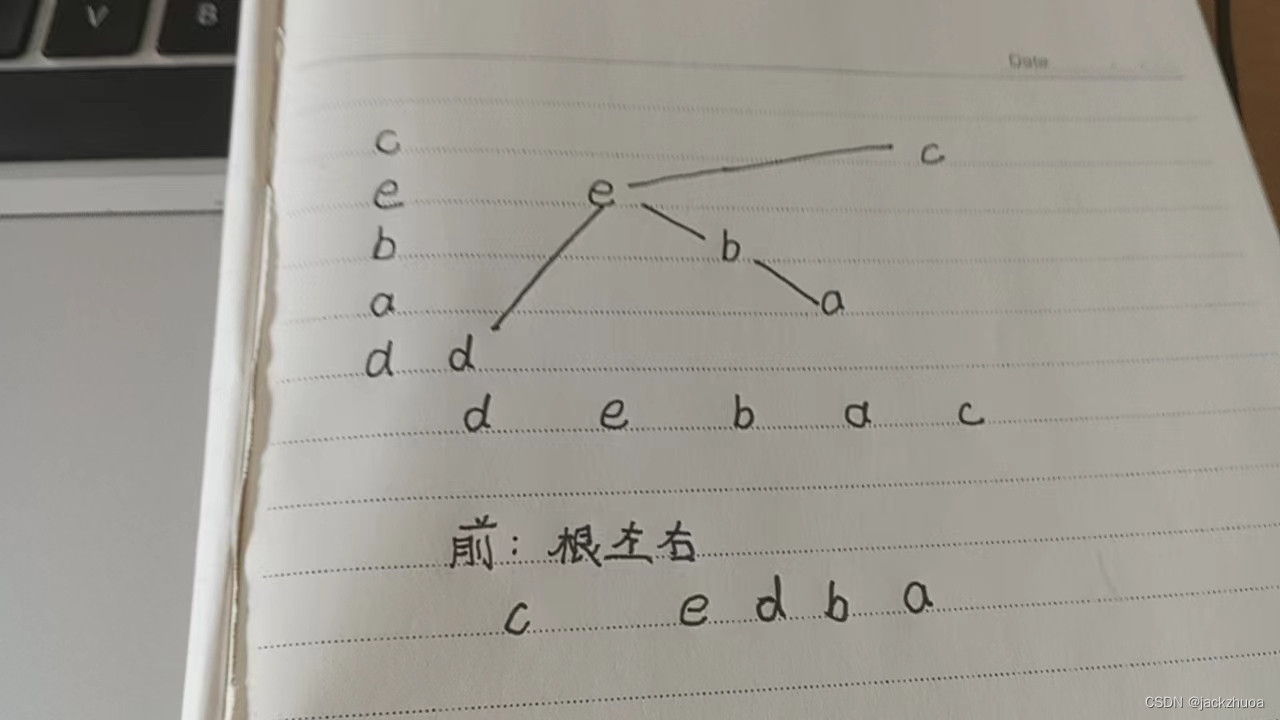
已知某二叉树的后序遍历序列是dabec, 中序遍历序列是debac , 它的前序遍历是( )。
二叉树的先序遍历和中序遍历如下: 先序遍历:EFHIGJK,中序遍历: HFIEJKG 。该二叉树根的右子树的根是:g\
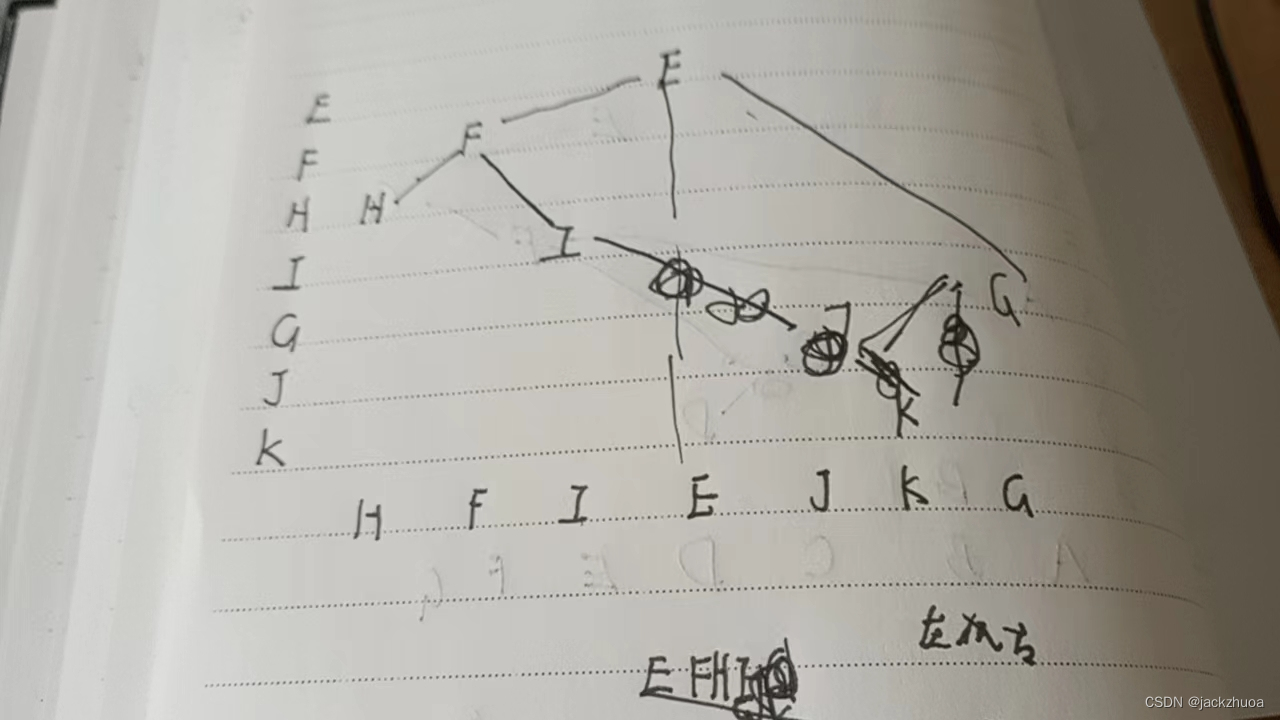
在二叉树结点的先序序列,中序序列和后序序列中,所有叶子结点的先后顺序( 完全相同)。
某二叉树的前序序列和后序序列正好相反,则该二叉树一定是( 高度等于其结点数)的二叉树。
在完全二叉树中,若一个结点是叶结点,则它没(左子结点和右子结点 )。
在下列情况中,可称为二叉树的是( 哈夫曼树)。
100个结点的完全二叉树的叶子结点数( 50 )个
完全二叉树的第6层有10个结点,那么共有(41)个结点。
前五层有2的5次方减1,为31,加上第六层,为41
完全二叉树的第6层有10个结点,那么有()个叶子结点。
相关文章:

数据结构习题(快期末了)
一个数据结构是由一个逻辑结构和这个逻辑结构上的一个基本运算集构成的整体。 从逻辑关系上讲,数据结构主要分为线性结构和非线性结构两类。 数据的存储结构是数据的逻辑结构的存储映像。 数据的物理结构是指数据在计算机内实际的存储形式。 算法是对解题方法和…...

Http协议:Http缓存
文章目录 Cookie和Session缓存有效性检查整体流程总结Cookie和Session Cookie 客户端的缓存 Session 服务端的缓存,存储服务器与客户端一次会话的过程中的数据/资源 两者区别 是服务端与客户端的不同需求造成的 有效期 Cookie的有效期很长,Session的较短 原因:服务…...

idea插件开发之hello idea plugin
写在前面 最近一直想研究下自定义idea插件的内容,这样如果是想要什么插件,但又一时找不到合适的,就可以自己来搞啦!这不终于有时间来研究下,但过程可谓是一波三折,再一次切身体验了下万事开头难。那么&…...

Sm4【国密4加密解密】
当我们开发金融、国企、政府信息系统时,不仅要符合网络安全的等保二级、等保三级,还要求符合国密的安全要求,等保测评已经实行很久了,而国密测评近两年才刚开始。那什么是密码/国密?什么是密评?本文就关于密…...

git如果将多次提交压缩成一次
将N个提交压缩到单个提交中有两种方式: git reset git reset的本意是版本回退,回退时可以选择保留commit提交。我们基于git reset的作用,结合新建分支,可以实现多次commit提交的合并。这个不需要vim编辑,很少有冲突。…...

android用Retrofit进行网络请求和解析
Retrofit 的原理 Retrofit的核心原理包括动态代理与Service Method的构建、注解解析与请求配置、网络请求执行与响应处理等。它是一个类型安全的HTTP客户端,用于Android和Java平台,通过将HTTP API转化为Java接口的方式,简化了网络请求的编写…...

list容器的基本使用
目录 前言一,list的介绍二,list的基本使用2.1 list的构造2.2 list迭代器的使用2.3 list的头插,头删,尾插和尾删2.4 list的插入和删除2.5 list 的 resize/swap/clear 前言 list中的接口比较多,与string和vector类似&am…...

34万汉语词语成语反义词ACCESS\EXCEL数据库
反义词就是两个意思相反的词,包括:绝对反义词和相对反义词。分为成对的意义相反、互相对立的词。如:真——假,动——静,拥护——反对。这类反义词所表达的概念意义互相排斥。或成对的经常处于并举、对待位置的词。如&a…...

yum方式更新Jenkins
目的 使用yum方式更新Jenkins。 步骤 查看最新可用版本 $ yum list jenkins Last metadata expiration check: 0:03:44 ago on Fri Jun 14 06:10:01 2024. Installed Packages jenkins.noarch 2.452.1-1.1 jenkins Available Pa…...

欢乐钓鱼大师保姆级教程,云手机辅助攻略解析!
在这份攻略中,我们将为大家详细介绍如何在《欢乐钓鱼大师》中快速提升钓鱼技能和游戏进展,避免常见的新手误区和不必要的资源浪费。无论是钓鱼点的选择、装备的合理使用还是技能的优化,我们都会一一为您详细解析,帮助您成为一名优…...
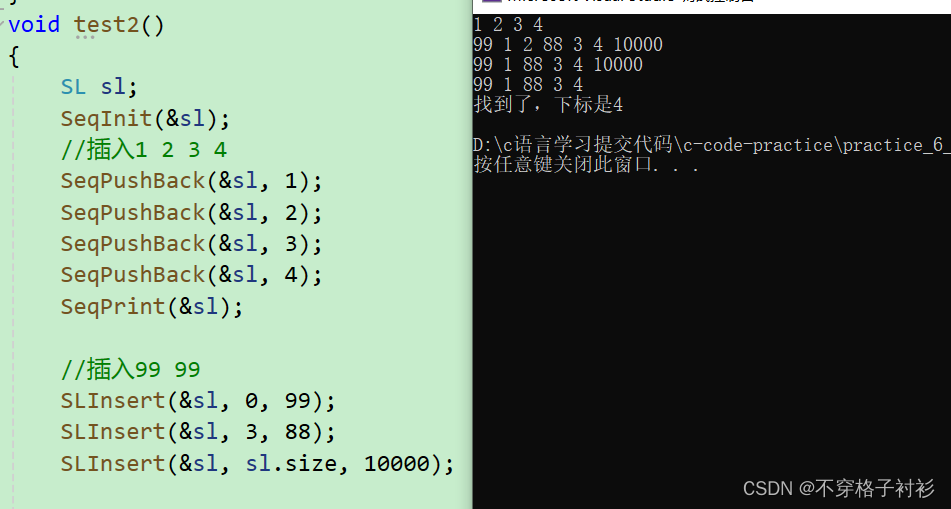
数据结构:手撕代码——顺序表
目录 1.线性表 2.顺序表 2.1顺序表的概念 2.2动态顺序表实现 2.2-1 动态顺序表实现思路 2.2-2 动态顺序表的初始化 2.2-3动态顺序表的插入 检查空间 尾插 头插 中间插入 2.2-4 动态顺序表的删除 尾删 头删 中间删除 2.2. 5 动态顺序表查找与打印、销毁 查找 …...

jenkins使用注意问题
1.在编写流水线时并不知道当前处在哪个目录,导致名使用不当,以及文件位置不清楚 流水线任务默认路径是,test4_mvn为jenkins任务名 [Pipeline] sh (hide)pwd /var/jenkins_home/workspace/test4_mvn maven任务也是,看来是一样的…...

Kaggle -- Titanic - Machine Learning from Disaster
新手kaggle之旅:1 . 泰坦尼克号 使用一个简单的决策树进行模型构建,达到75.8%的准确率(有点低,但是刚开始) 完整代码如下: import pandas as pd import numpy as npdf pd.read_csv("train.csv&quo…...

蓝牙音频解码芯片TD5163介绍,支持红外遥控—拓达半导体
蓝牙芯片TD5163A是一颗支持红外遥控、FM功能和IIS音频输出的蓝牙音频解码芯片,此颗芯片的亮点在于同时支持真立体声&单声道、TWS功能、PWM、音乐频谱和串口AT指令控制等功能,芯片在支持蓝牙无损音乐播放的同时,还支持简单明了的串口发送A…...
windows 下 docker 入门
这里只是具体过程,有不清楚的欢迎随时讨论 1、安装docker ,除了下一步,好像也没有其他操作了 2、安装好docker后,默认是运行在linux 下的,这时我们需要切换到windows 环境下, 操作:在右下角d…...

《别让“想太多”挡了你的骑行路,对比一下更丝滑》
在探索骑行的世界时,我们往往会被一些先入为主的想法所束缚。本文将带你对比骑行与其他运动和生活方式,揭示那些阻碍你爱上骑行的认知误区。 一、年龄不是界限:骑行与跑步的比较与跑步相比,骑行同样适合所有年龄段,但它…...
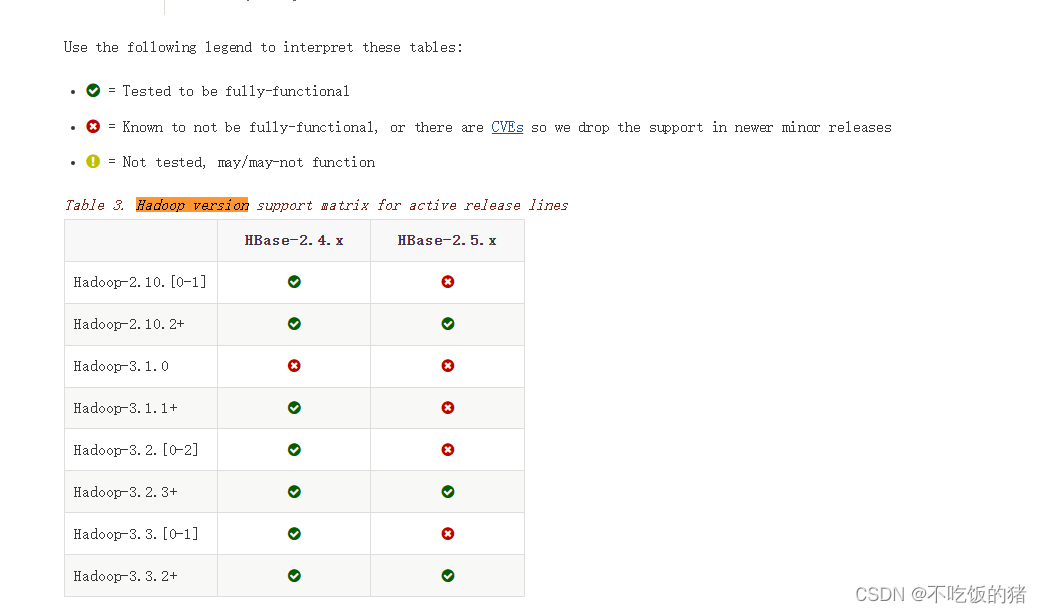
hadoop和hbase对应版本关系
https://hbase.apache.org/book.html#configuration...
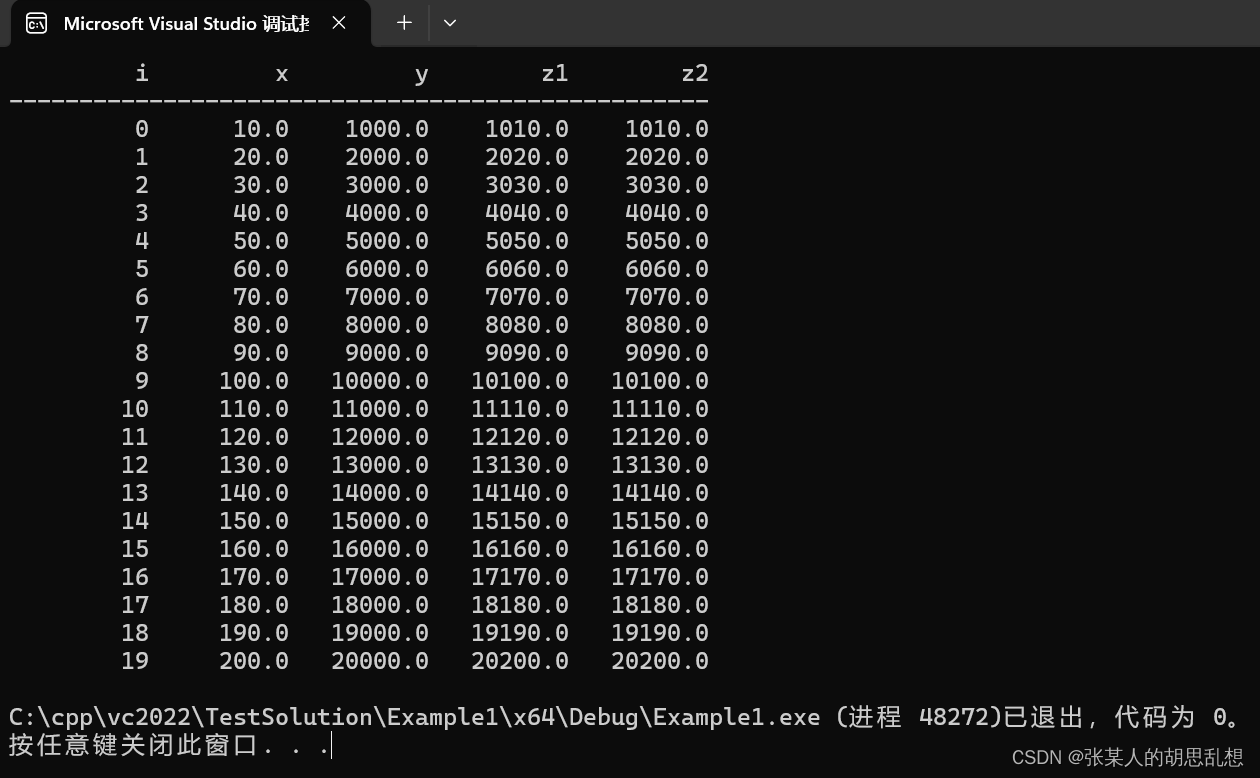
现代X86汇编-C和ASM混合编程举例
端午假期安装好了vs c2022,并写了个简单的汇编代码,证明MASM真的可以运行。今天需要搞一个实实在在的C和ASM混合编程的例子,因为用纯汇编的求伯君写WPS的时代一去不复返了。个别关键函数用汇编,充分发挥CPU的特色功能,偶尔还是需要…...

485. 最大连续 1 的个数
给定一个二进制数组 nums , 计算其中最大连续 1 的个数。 示例 1: 输入:nums [1,1,0,1,1,1] 输出:3 解释:开头的两位和最后的三位都是连续 1 ,所以最大连续 1 的个数是 3.示例 2: 输入:nums […...
席卷的B站《植物大战僵尸杂交版》V2.0.88整合包,PC和手机可用,含通关存档和视频教程!
今天给大家安利一款席卷B站,火爆全网的游戏——《植物大战僵尸杂交版》2.0.88整合包。 这个是网络上现存植物大战僵尸杂交版的最全整合,包含了修改工具,超强通关存档和高清工具。工具包有安装视频教程,支持手机版和pc多端使用&am…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
