回溯算法练习题(2024/6/10)
1组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,4], ]
示例 2:
输入:n = 1, k = 1 输出:[[1]]
提示:
1 <= n <= 201 <= k <= n
思路:
回溯法三部曲
-
递归函数的返回值以及参数:
- 返回值:无,使用类成员变量result存储最终结果。
- 参数:backtracking函数接受三个参数,分别是n(1到n的范围)、k(组合的长度)、startIndex(当前处理的起始位置)。
-
回溯函数终止条件:
- 当path的长度等于k时,将当前path加入结果集,然后返回。
-
单层搜索的过程解题思路:
- 从startIndex到n的范围内遍历所有可能的数字。
- 将当前处理的数字i添加到path中,表示选择了这个数字。
- 进行递归调用backtracking函数,继续向下搜索,但是startIndex更新为i+1,表示下一次搜索时不再考虑当前数字i之前的数字。
- 当递归返回后,将当前处理的数字i从path中弹出,进行回溯操作,尝试其他可能的组合。
- 通过不断选择、判断和回溯操作,搜索所有符合条件的组合,最终将结果存储在result中并返回。
代码:
class Solution {
private:vector<vector<int>> result; // 存放符合条件结果的集合vector<int> path; // 用来存放符合条件结果void backtracking(int n, int k, int startIndex) {if (path.size() == k) { // 如果路径长度等于k,将路径加入结果集result.push_back(path);return;}for (int i = startIndex; i <= n; i++) {path.push_back(i); // 处理节点backtracking(n, k, i + 1); // 递归path.pop_back(); // 回溯,撤销处理的节点}}
public:vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1); // 从1开始尝试组合return result; // 返回结果集}
};2 组合总和 III
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7 输出: [[1,2,4]] 解释: 1 + 2 + 4 = 7 没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]] 解释: 1 + 2 + 6 = 9 1 + 3 + 5 = 9 2 + 3 + 4 = 9 没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1 输出: [] 解释: 不存在有效的组合。 在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
提示:
2 <= k <= 91 <= n <= 60
思路:
-
递归函数的返回值和参数:
- 返回值:无,结果保存在类成员变量result中。
- 参数:backtracking函数接受四个参数,分别是目标和targetSum、组合的长度k、当前组合的和sum、当前可以选数字的最小索引startIndex。
-
回溯函数的终止条件:
- 如果当前的和sum超过了目标和targetSum,则不再搜索直接返回。
- 如果当前组合的长度path等于k,且当前的和sum等于目标和targetSum,则将当前组合加入结果集合result。
-
单层搜索的过程解题思路:
- 从startIndex开始,遍历所有可选的数字。
- 将当前数字i加入组合path中,累加当前和sum。
- 递归调用backtracking函数,继续搜索下一个数字。
- 递归返回后,从当前和sum中减去当前数字i,从组合path中移除当前数字i。
- 通过不断的加入数字、递归搜索和移除数字,最终得到所有满足条件的组合。
代码:
class Solution {
private:vector<vector<int>> result; // 存放结果集合vector<int> path; // 用来存放当前组合// 回溯函数,生成和为 targetSum,长度为 k 的数字组合void backtracking(int targetSum, int k, int sum, int startIndex) {// 如果当前的sum已经超过了目标值,则不再搜索直接返回if (sum > targetSum) return;// 达到组合长度要求且总和等于目标值时,将当前组合加入结果集合if (path.size() == k) {if (sum == targetSum) result.push_back(path);return;}// 从 startIndex 开始遍历可选数字for (int i = startIndex; i <= 9; i++) {sum += i; // 统计当前总和path.push_back(i); // 将当前数字加入组合中backtracking(targetSum, k, sum, i + 1); // 递归处理下一个数字sum -= i; // 回溯,撤销当前数字的处理path.pop_back(); // 回溯,撤销当前数字的处理}}public:// 组合函数,生成和为 n,长度为 k 的数字组合vector<vector<int>> combinationSum3(int k, int n) {backtracking(n, k, 0, 1); // 回溯搜索组合return result; // 返回结果集合}
};3组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates =[2,3,6,7],target =7输出:[[2,2,3],[7]] 解释: 2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选, 7 = 7 。 仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates的所有元素 互不相同1 <= target <= 40
思路:
-
递归函数的返回值和参数:
- 返回值:无,结果保存在类成员变量result中。
- 参数:backtracking函数接受四个参数,分别是候选数字数组candidates、目标和target、当前组合的和sum、当前可以选数字的最小索引startIndex。
-
回溯函数的终止条件:
- 如果当前的和sum超过了目标和target,则不再搜索直接返回。
- 如果当前组合的和sum等于目标和target,则将当前组合加入结果集合result。
-
单层搜索的过程解题思路:
- 从startIndex开始,遍历候选数字数组candidates。
- 将当前数字加入组合path中,累加当前和sum。
- 递归调用backtracking函数,继续搜索当前数字。
- 递归返回后,从当前和sum中减去当前数字,从组合path中移除当前数字。
- 通过不断的加入数字、递归搜索和移除数字,最终得到所有满足条件的组合。
代码:
class Solution {
private:vector<vector<int>> result; // 存放结果集合vector<int> path; // 用来存放当前组合void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {if (sum > target) {return; // 当前组合和超过目标值,终止搜索}if (sum == target) {result.push_back(path); // 当前组合和等于目标值,加入结果集合return;}for (int i = startIndex; i < candidates.size(); i++) {sum += candidates[i]; // 统计当前总和path.push_back(candidates[i]); // 将当前数字加入组合中backtracking(candidates, target, sum, i); // 递归处理当前数字sum -= candidates[i]; // 回溯,撤销当前数字的处理path.pop_back(); // 回溯,撤销当前数字的处理}}public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backtracking(candidates, target, 0, 0); // 回溯搜索组合return result; // 返回结果集合}
};相关文章:
)
回溯算法练习题(2024/6/10)
1组合 给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。 示例 1: 输入:n 4, k 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,4], ] 示例 2: 输入:n …...

机器学习--线性模型和非线性模型的区别?哪些模型是线性模型,哪些模型是非线性模型?
文章目录 引言线性模型和非线性模型的区别线性模型非线性模型 总结线性模型非线性模型 引言 在机器学习和统计学领域,模型的选择直接影响到预测的准确性和计算的效率。根据输入特征与输出变量之间关系的复杂程度,模型可以分为线性模型和非线性模型。线性…...

[linux] Qwen2Tokenizer报错 transformers版本问题
上午没问题,下午pull了新代码,就有了报错。。 发现是transformers版本问题。但。。其实我都默认安的是最新版本。。 也许这就是人生吧。。 报错: File "/Pai-Megatron-Patch/megatron_patch/tokenizer/__init__.py", line 213…...
)
算法刷题笔记 单链表(C++实现)
文章目录 题目描述基本思路实现代码 题目描述 实现一个单链表,链表初始为空,支持三种操作: 向链表头插入一个数;删除第 k个插入的数后面的一个数;在第 k个插入的数后插入一个数。 现在要对该链表进行M次操作&#x…...

Oracle 排查慢SQL
Oracle 排查慢SQL select * from v s q l a r e a w h e r e r o w n u m < 10 ; s e l e c t ∗ f r o m v sqlarea where rownum<10; select * from v sqlareawhererownum<10;select∗fromvsql where rownum<10; select * from dba_hist_sqltext where rownum<…...
)
java技术专家面试指南80问【java学习+面试宝典】(七)
Dubbo需要 Web 容器吗? 不需要,如果硬要用 Web 容器,只会增加复杂性,也浪费资源。 PrintStream、BufferedWriter、PrintWriter的比较? PrintStream类的输出功能非常强大,通常如果需要输出文本内容,都应…...

4机器学习期末复习
在机器学习中,数据清洗与转换包括哪些内容? 对数据进行初步的预处理,需要将其转换为一种适合机器学习模型的表示形式对许多模型类型来说,这种表示就是包含数值数据的向量或者矩阵: 1)将类别数据编码成为对…...

chatgpt: int t[] int *t 区别
在C语言中,int t[]和int *t虽然在某些情况下可以相互替换,但它们有一些关键的区别。这些区别主要体现在声明的语义、内存分配方式和使用场景上。以下是详细的解释: ### 1. int t[] #### 语义: - int t[]声明了一个数组,t是一个数…...
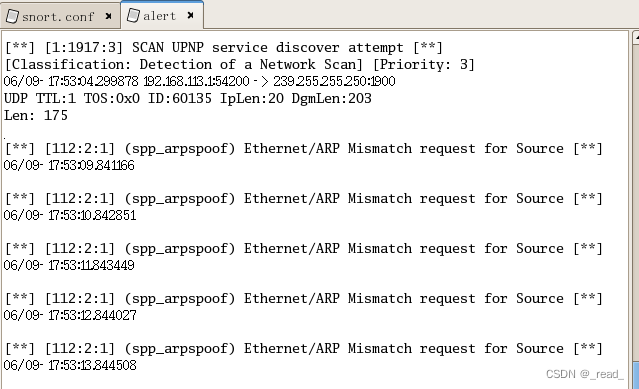
网络安全技术实验六 入侵检测技术实践
一、实验目的和要求 理解基于网络的入侵检测系统的基本原理,掌握snort IDS工作机理; 学习应用snort三种方式工作;熟练编写snort规则; 完成snort数据包记录、日志查看、字符串匹配、ARP欺骗攻击检测、端口扫描工具检测等功能。 …...

SpringBoot中获取当前请求的request和response
在Spring Boot中,你可以以多种方式获取当前请求的HttpServletRequest和HttpServletResponse对象。以下是几种常见的写法示例: 1. 在方法参数中声明 最常见和推荐的方式是在控制器方法的参数中直接声明HttpServletRequest和HttpServletResponse对象。Sp…...
Neo4j 桌面版打不开踩坑贴
真的踩坑。。。没有人告诉我为啥桌面版和社区版不能一起下啊!! 我是先下载了社区版之后再下载的桌面版,结果桌面版界面一直打不开。 尝试了网上多种办法都没效果,好多都是说jdk不兼容导致无法打开,让我从JDK 17 ->…...

[数据集][目标检测]中国象棋检测数据集VOC+YOLO格式300张12类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):300 标注数量(xml文件个数):300 标注数量(txt文件个数):300 标注类别…...

全方位·多层次·智能化,漫途水库大坝安全监测方案
党的十九届五中全会提出,到2025年前,完成新出现病险水库的除险加固,配套完善重点小型水库雨水情和安全监测设施,实现水库安全鉴定和除险加固常态化。 加快推进小型水库除险加固。加快构建气象卫星和测雨雷达、雨量站、水文站组成…...

windows安装SQLyog
windows安装SQLyog 1. 下载 SQLyog 安装包 访问 SQLyog 的官方网站。在网站上找到下载链接,通常会有一个“Download”或“Try Now”按钮。如果需要注册或填写信息以获取下载链接,请按提示操作。 2. 运行安装程序 下载完成后,双击运行下载…...

jEasyUI 转换 HTML 表格为数据网格
jEasyUI 转换 HTML 表格为数据网格 jEasyUI 是一个基于 jQuery 的框架,它为用户提供了一套完整的用户界面组件,使得网页开发变得更加简单快捷。在本文中,我们将探讨如何使用 jEasyUI 将一个普通的 HTML 表格转换为功能丰富的数据网格(datagrid)。 为什么使用数据网格? …...
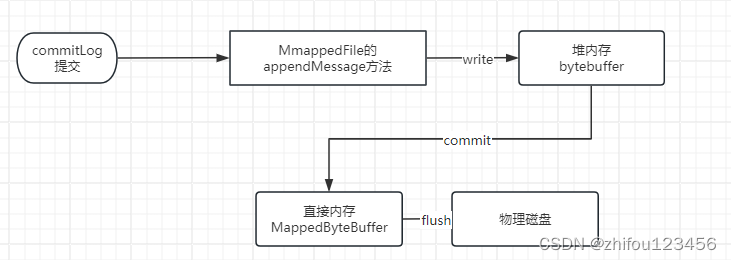
深度解析RocketMq源码-持久化组件(一) MappedFile
1. 绪论 rocketmq之所以能够有如此大的吞吐量,离不开两个组件,一个是利用netty实现的高性能网络通信组件;另一个就是利用mmap技术实现的存储组件。而在rocketmq的存储组件中主要有三个组件,分别是持久化文件commitLog,…...
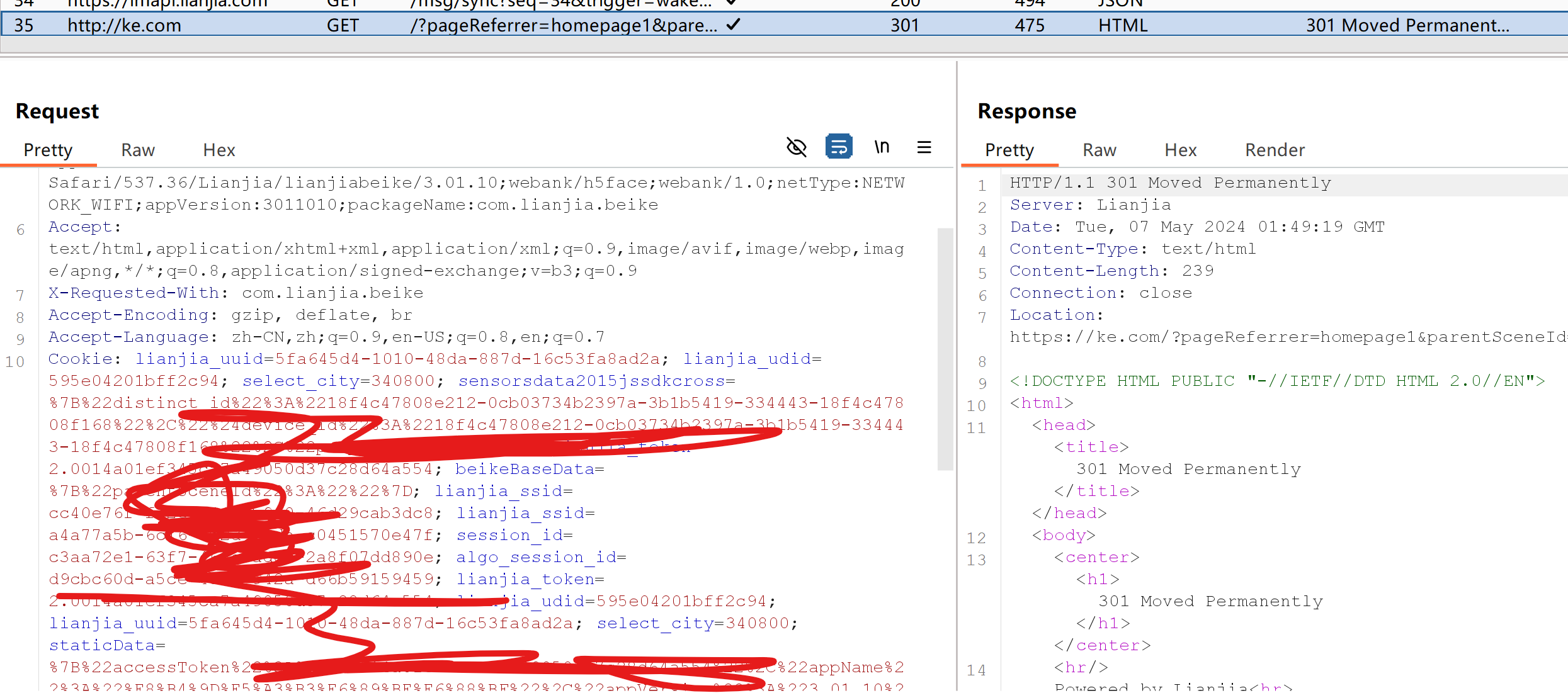
贝壳APP渗透测试WP
前期配置 环境说明 使用PIXEL 4手机,为Android 12系统 APP名为贝壳找房,包名com.lianjia.beike,版本号3.01.10,截至2024/05/07为最新版,小米应用市场下载 绕过反Frida机制 可以参考往期推送,《绕过最新…...

IDEA快速入门02-快速入门
二、快速入门 2.1 打开IDEA,点击New一个项目 入口,依次打开 File -> New -> Project。 2.2 使用Spring Initializr方式构建Spring Boot项目 2.3 设置项目所属组、项目名称、java版本等 2.4 选择SpringBoot版本及依赖组件 点击Create进行创建。 2.6 创建成…...

快速构建本地RAG聊天机器人:使用LangFlow和Ollama实现无代码开发
基于LangChain的快速RAG应用原型制作方法 还记得构建智能聊天机器人需要数月编码的日子吗? LangChain这样的框架确实简化了开发流程,但对非程序员来说,数百行代码仍然是一道门槛。 有没有更简单的方法呢? 图片由 Ravi Palwe 在…...
关于使用pycharm中控制台运行代码错误之FileNotFoundError: [Errno 2] No such file or directory:
在使用pycharm环境下复现《python编程:从入门到实践》这本书第16.1.1内容中分析csv文件头一节的代码时出现如下问题: 1、文章中使用的数据来源问题 直接参考本站Kenny C同学的文章提供内容即可。 https://github.com/kenidi8215/Hello-World 打开网页&a…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
