现代密码学-国密算法
商用密码算法种类

商用密码算法
密码学概念、协议与算法之间的依赖关系
数字签名、证书-公钥密码、散列类算法
消息验证码-对称密码 ,散列类
安全目标与算法之间的关系
机密性--对称密码、公钥密码
完整性--散列类算法
可用性--散列类、公钥密码
真实性--公钥密码
不可否认--公钥密码
SM2椭圆曲线公钥加密
公钥密码体制
公钥体制加密
- 接收者B产生一对密钥:私钥--
,公钥--
- A想向B发消息m,则使用B的公钥加密m,表示为
, c是加密后的密文,
是加密算法
- B收到密文c后,用自己的私钥
解密,表示为
,D是解密算法
只能由B进行解密
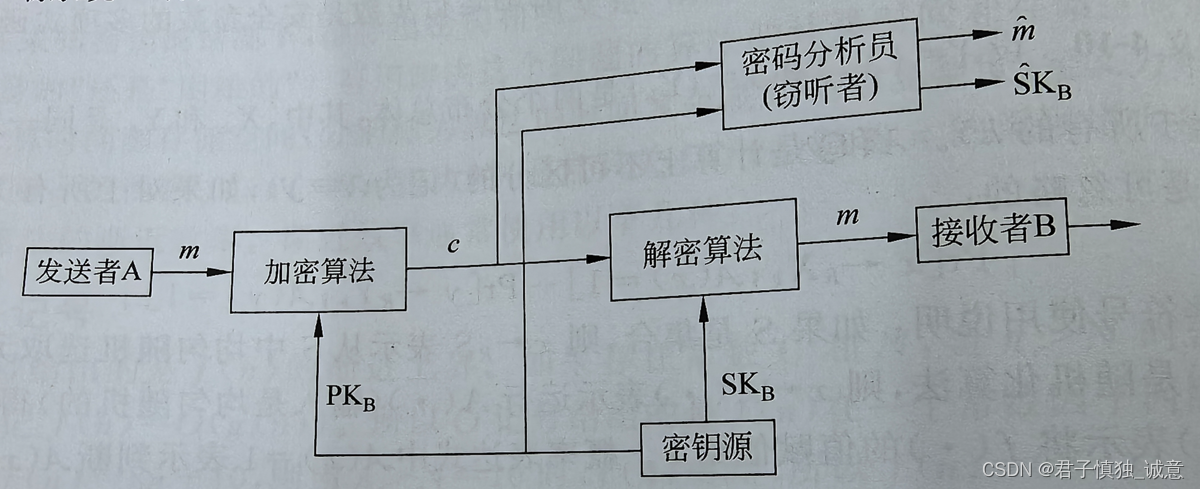
公钥体制认证
用户A用自己的私钥对m进行加密,,将c发给B,B用A的公钥解密
从m得到c的过程是经过A的私钥加密的,只能A才能做到,因此c可以当作A对m的数字签名。

双重加密、解密
为了同时具有保密功能和认证功能,可以使用双重加、解密
发送方先用自己的私钥对消息加密,用于提供数字签名。再用接收方的公钥加密,表示为
接收者收到后,x先用自己的私钥,再用发送方的公钥进行两次解密,解密过程为

椭圆曲线密码体制
椭圆曲线密码 Elliptic CurveCryptography ECC:利用椭圆曲线实现密码技术
椭圆曲线上的离散对数问题
本质:已知xG求数x的问题
椭圆曲线密码中,先确定一条椭圆曲线,然后对椭圆曲线上的某一些点之间的“运算”进行定义,利用这些“运算”来进行密码技术相关的计算。
已知
椭圆曲线E
椭圆曲线E上的一点G(基点)
椭圆曲线上的一点xG(G的x倍)
求解
数x
椭圆曲线Diffie-Hellman密钥交换
AB需要共享一个对称密码的密钥,用椭圆曲线Diffie-Hellman密钥交换,生成共享密钥
- A向B发送点G。G被窃听无影响
- A生成随机数a,将a作为A的私钥
- B生成随机数b,将b最为B的私钥
- A向B发送点aG
- B向A发送bG
- A对收到的bG计算其在椭圆曲线上a倍的点,a(bG)=abG==共享密钥
- B对收到的aG计算其在椭圆曲线上b倍的点,b(aG)=baG=abG==共享密钥
每次通信使用不同的随机数,共享密钥也会随之改变==保证了前向安全性forward secrecy
SM2
SM2是国家密码管理局颁布的中国商用公钥密码标准算法,是一组椭圆曲线密码算法,包含加解密算法、数字签名算法。
SM2与国际ECC比较
ECC算法采用国际机构建议的曲线和参数,SM2算法的参数需要利用一定的算法产生,算法中加入了用户特异性的曲线参数、基点、用户的公钥点信息,安全性更高
ECC中,用户可以选择MD5或SHA-1等国际通用的哈希算法,SM2使用SM3哈希算法,SM3哈希算法输出为256比特,与SHA-256算法安全性相当
SM2椭圆曲线公钥密码加密算法
基本参数
基于素数域的SM2算法参数如下:
的特征p为m比特长的素数,p要尽可能大;
长度不小于192比特的比特串SEED;
上的2个元素a,b,满足
,定义曲线
基点;
G的阶n为m比特长的素数,满足;
余因子,其中
是曲线
的点数。
SEED,a,b产生的算法:
- 任意选取长度不小于192比特的比特串SEED;
- 计算
,记
,其中
表示256比特输出的SM3哈希算法
- 取
;
- 取
;
- 在
上任意选择2个元素a,b,满足
;
- 若
,则返回1;
- 所选择的
上的曲线是
- 输出(SEED,a,b)
密钥产生
假设接收方为B,B的秘密钥取{1,2,...,n-1}中的一个随机数,记为
,其中G的阶n
B的公开钥取为椭圆曲线上的点:,其中,
是基点
加密算法
假设发送方是A,A要发送的消息表示为M比特串,M的长度为klen.算法如下:
- 选择随机数
- 计算椭圆曲线点
,将x1,y1表示为比特串;
- 计算椭圆曲线点
,若S为无穷远点,则报错退出;
- 计算椭圆曲线
,将x2,y2表示为比特串;
- 计算
,若t为全0的比特串,则返回1;
- 计算
----(mod 2 加法)
- 计算
- 输出密文C=(C1,C2,C3)
KDF(*)是密钥派生函数,本质为一个伪随机数产生函数,用来产生密钥,这里KDF为SM3,第(3)步的H也是SM3
解密算法
B收到密文C后,进行解密,过程如下:
- 从C中取出C1,将C1表示为椭圆曲线上的点,验证C1是否满足椭圆曲线方程。不满足就报错退出;
- 计算椭圆曲线点
,若S为无穷远点,则报错退出;
- 计算
,将x2,y2表示为比特串;
- 计算
,若t为全0的比特串,则报错退出;
- 从C中取出C2,计算
;
- 计算
,从C中取出C3,若
则报错退出;
- 输出明文
SM2椭圆曲线公钥密码签名算法
基本参数
与前面加密算法的参数设置相同
密钥产生
与与前面加密算法产生方法一样,记为
设是A的长度为
比特的标识,
由
转换而成的两个字节,A计算
,其中a,b是椭圆曲线方程的参数,
是基点G的坐标,
是
的坐标。将这些值转换为比特串后,在进行
。验证方B验证签名时,也需要计算
签名算法
设待签名的消息为M,操作如下:
- 取
- 计算
,将e转换为整数,Hv是输出为v比特长的哈希函数
- 用随机数产生器生成随机数
- 计算椭圆曲线点
;
- 计算
,若r=0或者r+k=n,则返回3
- 计算
,若s=0,则返回3
- 消息M的签名为(r,s)
验证算法
B收到消息以及其签名
,进行验证操作:
检验是否成立,若不成立,验证失败;
检验是否成立,若不成立,验证失败;
置
计算,并将其转换为整数;
计算,若t=0,验证失败
计算椭圆曲线点
计算,检查
是否成立,若成立则验证通过,否则,验证失败
相关文章:
现代密码学-国密算法
商用密码算法种类 商用密码算法 密码学概念、协议与算法之间的依赖关系 数字签名、证书-公钥密码、散列类算法 消息验证码-对称密码 ,散列类 安全目标与算法之间的关系 机密性--对称密码、公钥密码 完整性--散列类算法 可用性--散列类、公钥密码 真实性--公…...
Postman简介
目录 1.概述 2.诞生背景 3.历史版本 4.安装和卸载 5.菜单和菜单项 6.使用 7.应用场景 8.示例 8.1.简单的GET请求 8.2.POST请求提交数据 8.3.查询参数 9.未来展望 10.总结 1.概述 Postman是一款用于API开发、测试和文档管理的综合性工具。允许开发者和测试人员创建…...
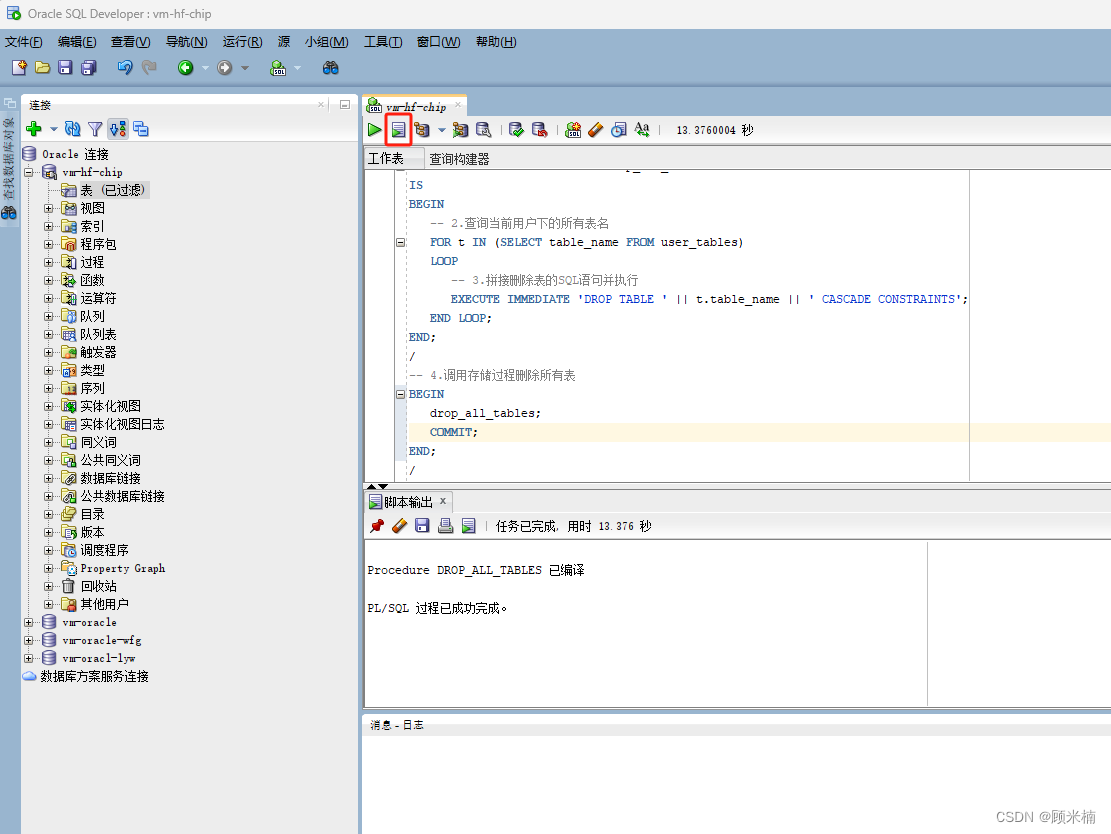
oracle 删除当前用户下所有表
荆轲刺秦王 通常呢 我们将正式环境的 oracle 数据库 导出成 dmp 文件,然后导入到测试环境或者本地环境,期间可能会出现各种问题。那么如何使错误的导入数据全部删除呢。可以这样做: 1. 本地虚拟机启动 oracle 服务 2. sqldeveloper 连接 o…...

探索C嘎嘎的奇妙世界:第二关---C++的输入与输出
1 C的输入与输出: 新生婴儿会以自己独特的方式向这个崭新的世界打招呼,C刚出来后,也算是一个新事物, 那C是否也应该向这个美好的世界来声问候呢?我们来看下C是如何来实现问候的呢? 在 C的不断发展中,出现了许多新的头…...

实现思路:Vue 子组件高度不固定下实现瀑布流布局
实现思路:Vue 子组件高度不固定下实现瀑布流布局 一、瀑布流布局基础实现原理 在深入解说不定高度子组件的瀑布流如何实现之前,先大体说一下子组件高度固定已知的这种实现原理: 有一个已知组件高度的数组。定义好这个瀑布流的列数ÿ…...

构建实时搜索与推荐系统:Elasticsearch与业务结合
在当今这个信息爆炸的时代,搜索引擎和推荐系统已成为我们日常生活中不可或缺的一部分。它们不仅帮助我们快速找到所需信息,还根据我们的喜好推荐相关内容,提升了用户体验。本文将探讨如何使用Elasticsearch构建实时搜索与推荐系统,…...

鸿蒙 如何将base64的图片保存到相册
把一个base64图片 保存到鸿蒙手机 相册中怎么实现呢? 下面有2中方法 方案一:可以通过安全控件「保存控件(SaveButton)」实现。该控件对应媒体库写入特权。应用集成保存控件后,用户点击该控件,应用会获取1…...

高速公路智能管理系统:构建安全畅通的数字大动脉
随着城市化进程的加速和交通需求的增长,高速公路系统作为城市交通的重要组成部分,正承担着越来越多的交通运输任务。为了提升高速公路的安全性、便捷性和智能化管理水平,高速公路智能管理系统应运而生。本文将深入探讨高速公路智能管理系统的…...

基于Java自习室在线预约系统 的设计与实现
博主介绍: 大家好,本人精通Java、Python、C#、C、C编程语言,同时也熟练掌握微信小程序、Php和Android等技术,能够为大家提供全方位的技术支持和交流。 我有丰富的成品Java、Python、C#毕设项目经验,能够为学生提供各类…...

摄像头校准之白平衡畸变坏点
摄像头校准之白平衡&畸变&坏点 1. 源由2. 校准内容3. 畸变校准一、畸变模型二、校准步骤1. 准备工作2. 特征点检测3. 计算内参数和畸变系数4. 畸变校正 三、验证和优化1. 视觉验证2. 误差评估3. 参数优化 4. 白平衡校准一、白平衡基础二、自动白平衡(AWB&am…...

【C++进阶】模板进阶与仿函数:C++编程中的泛型与函数式编程思想
📝个人主页🌹:Eternity._ ⏩收录专栏⏪:C “ 登神长阶 ” 🤡往期回顾🤡:栈和队列相关知识 🌹🌹期待您的关注 🌹🌹 ❀模板进阶 🧩<&…...

OpenCV之cv::Scalar
在 OpenCV 中,cv::Scalar 是一个模板类,用于表示多通道的值。常用来表示颜色或其他具有多个分量的数据。在图像处理中,cv::Scalar 经常用于指定颜色。 cv::Scalar(255, 255, 255) 具体如何理解,取决于图像的颜色空间:…...

智能合约与身份验证:区块链技术的创新应用
一、引言 区块链,一个近年来备受瞩目的技术名词,已经从最初的数字货币领域扩展到了众多行业。那么,究竟什么是区块链?它为何如此重要?本文将深入剖析区块链技术的原理、应用及未来发展。 二、区块链的基本概念 区块…...
浔川身份证号码查询——浔川python科技社
Python获取身份证信息 公民身份号码是每个公民唯一的、终身不变的身份代码,由公安机关按照公民身份号码国家标准编制。每一个居民只能拥有一个唯一的身份证,它是用于证明持有人身份的一种法定证件。 身份证包含了个人的一些重要信息,比如&am…...

C++的标准容器及其应用
C的标准容器及其应用 数组(array)数组的特征应用实列 前向列表(forward_list)前向列表的特征应用实列 列表(list)列表的特征应用实列 有序映射(map)有序映射的特征应用实列 队列&…...

linux如何部署前端项目和安装nginx
要在Linux上部署前端项目并安装Nginx,你可以按照以下步骤操作: 安装Nginx: sudo apt update sudo apt install nginx 启动Nginx服务: sudo systemctl start nginx 确保Nginx服务开机自启: sudo systemctl enable nginx 部署前端项目,假设前…...

Coolify:24.2K 星星!使用全新、开源免费且自托管的替代方案,部署应用程序的最佳工具(停止使用 Vercel)
✨点击这里✨:🚀原文链接:(更好排版、视频播放、社群交流、最新AI开源项目、AI工具分享都在这个公众号!) Coolify:24.2K 星星!使用全新、开源免费且自托管的替代方案,部…...

Dubbo入门
Dubbo,听名字好像有点高大上,但实际上它就是个让不同的计算机程序之间能够互相交流的工具,专业点说,它是一个分布式服务框架。想象一下,你有好几个小团队,每个团队负责开发一个部分,最后这些部分…...

从零学习es8
配置 编辑 elasticsearch.yml xpack.security.enabled: true 单节点 discovery.type: single-node设置账号: elasticsearch-reset-password -u elastic 如果要将密码设置为特定值,请使用交互式 (-i) 参数运行该命令。 elasticsearch-reset-password -i…...
方法详解)
String.compareTo()方法详解
Java 中的 String.compareTo() 方法用于按字典顺序比较两个字符串。这个方法实现了 Comparable 接口,返回一个整数,表示字符串的相对顺序。 方法签名 public int compareTo(String anotherString)返回值 一个负整数:如果当前字符串在字典顺…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
