【动态规划】| 路径问题之最小路径和 力扣64
🎗️ 主页:小夜时雨
🎗️专栏:动态规划
🎗️如何活着,是我找寻的方向
目录
- 1. 题目解析
- 2. 代码
1. 题目解析
题目链接: https://leetcode.cn/problems/minimum-path-sum/description/

这道题目和之前一道题 不同路径1力扣62: https://leetcode.cn/problems/unique-paths/description/ 有相似的地方, 建议先去看看那道题整理一下思路, 会简单一些.
通常动态规划的题目有五个大步骤进行解析, 接下来一一来进行分析.
1. 状态表示
动态规划的重点是状态表示, 我们通过状态表示才可以写出正确的状态转移方程, 状态表示我们通常都是根据 经验+题目 要求来进行定义的.
比如本道题又是一个二维的矩阵, 那么依旧可以定义我们的状态表示为
dp[i][j]: 表示到达 (i, j) 这个位置时, 路径上的数字总和为最小
2. 状态转移方程
- 根据题目要求, 假如我们走到了 (i,j) 位置时, 我们可以从上面往下走或者是从左面往右走, 即是从 (i-1, j) 或者 (i, j-1) 往 (i, j) 的位置走。
- 根据状态表示, dp[i][j] 的大小可以由两部分组成, 问的是路径总和为最小, 那么共有两条不同的路径: 从左往右走或者从上往下走,求的应该是这二者中的最小值。
- 从 (0, 0) 走到 (i-1, j) 的最小路径总和假设为 X , 那么从 (0, 0) 走到 (i, j) 的最小路径总和就是 X + nums[i][j], 注意要加上 (i,j)位置的数字。
- 正好所对应的就是 dp[i - 1][j] 所表示的含义. 同理 dp[i][j - 1] 也是. 那么状态转移方程应如下表示:
dp[i][j] = Math.min(dp[i - 1][j],dp[i][j - 1]) + nums[i][j]
- 但是有一个细节问题, 这里和不同路径1 不同的是, 这里需要用到原数组,我们通常也是采取多加一行一列的方式来避免出现 dp 表越界的情况, 所以要注意映射关系。
- 即是遍历 dp 表填表的过程中的 (i, j)对应原数组的值是 nums[i- 1][j - 1] 要注意,后面还会再强调一遍。
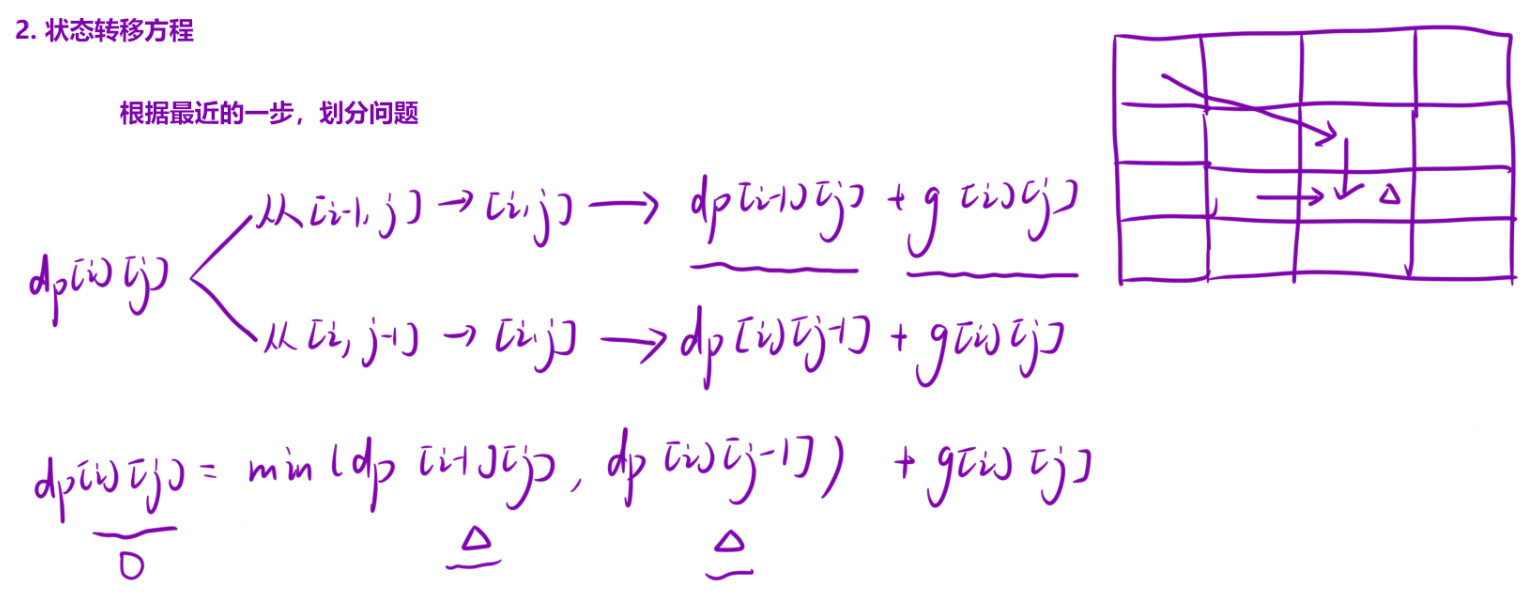
3. 初始化
细节问题: 观察状态转移方程可知, 有可能会有越界的风险, 此处我们依旧采取一种多加一行一列的方式来进行初始化.多加一行一列要保证两点:
- 虚拟节点的值要保证后面的dp 表里的值是正确的
- 要注意下标的映射关系. 因为我们是多加了一行一列, 所以对应到原始数组就应该行列要减一. (此处用到了原数组, 所以要有这个映射关系)
注意 :
这道题的初始化和前两道题有些许不同
- 原本的dp[0][0] 最小的路径和就是本身自己, 也就是 dp[0][0] = nums[0][0]. 因为我们多加了一行一列, 所以变成了 dp[1][1] = nums[0][0].
- 观察下图我们发现,填写 dp[1][1] 的时候需要用到左边和上边值, 因为求的是二者中的最小值, 为了不干扰结果, 设置为0即可。
- 看下图,但是填写 dp[1][2] 的时候,需要用到上面的值 dp[0][2] 和 dp[1][1] 作比较求最小值,倘如是dp[1][2] 还是默认初始化为 0 的话, 就会影响结果,使dp[1][2] = dp[0][2] + nums[0][1], 导致错误了.
- dp[1][2] 本该是只有一条路径, 那就是用到 (1,1)走到(1,2),就应该是 dp[1][2] = dp[1][1] + nums[0][1]. 观察结果,让 dp[0][2] 是一个非常大的数字,不影响结果即可。此处通常我们设置为整数最大值或者 0x3f3f3f3f.
看图更容易理解
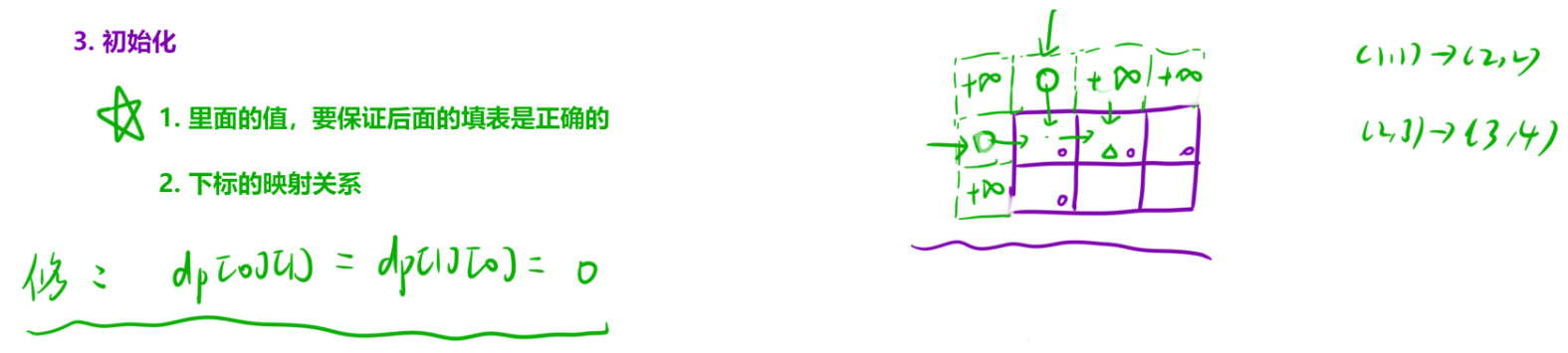
4. 填表顺序
观察可知, 填 (i, j) 的值的时候需要用到上一行和左边的值. 所以填表顺序是 从上往下, 从左往右.
5. 返回值
根据题目的要求, 要到达(m, n) 最小路径和是多少, 正好对应 dp[m][n] 的表示. 所以返回 dp[m][n] 即可.
2. 代码
动态规划的代码编写一般都是分为 4 个步骤进行:
- 创建 dp 表
- 初始化
- 填表
- 返回值
// 动态规划// 是不同路径1 的小幅改动版版: https://leetcode.cn/problems/unique-paths/public int uniquePathsWithObstacles(int[][] ob) {// 1.创建 dp表// 2.初始化// 3.填表// 4.返回值// 动态规划 这里的是二维, 所以时空都是O(M*N)int m = ob.length, n = ob[0].length;int[][] dp = new int[m + 1][n + 1];// dp[1][1] = 1;dp[0][1] = 1;// 做好映射关系, 原数组的(0,0) 对应dp表中的(1,1)// 这里填的是 dp 表, 所以建议从(1,1) 开始, 也就是dp表多加了一行一列// 如果是障碍的话, 就直接忽略, 默认就是 0, 也就是表示到不了for(int i = 1; i <= m; i++) { // 从上往下每一行for(int j = 1; j <= n; j++) { // 从左往右每一列if(ob[i - 1][j - 1] == 0) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}}return dp[m][n];}
🎗️🎗️🎗️ 好啦,到这里有关本题的分享就没了,如果感觉做的还不错的话可以点个赞,关注一下,你的支持就是我继续下去的动力,我们下期再见,拜了个拜~ ☆*: .。. o(≧▽≦)o .。.:*☆
相关文章:
【动态规划】| 路径问题之最小路径和 力扣64
🎗️ 主页:小夜时雨 🎗️专栏:动态规划 🎗️如何活着,是我找寻的方向 目录 1. 题目解析2. 代码 1. 题目解析 题目链接: https://leetcode.cn/problems/minimum-path-sum/description/ 这道题目和之前一道…...

如何在vector中插入和删除元素?
在C的std::vector中插入和删除元素通常使用其成员函数来完成。以下是如何在std::vector中插入和删除元素的示例: 插入元素 在末尾插入元素:使用push_back函数。 cpp复制代码 #include <vector> int main() { std::vector<int> v; v.push_…...
独具韵味的移动端 UI 风格
独具韵味的移动端 UI 风格...

【SpringBoot】SpringBoot:构建实时聊天应用
文章目录 引言项目初始化添加依赖 配置WebSocket创建WebSocket配置类创建WebSocket处理器 创建前端页面创建聊天页面 测试与部署示例:编写单元测试 部署扩展功能用户身份验证消息持久化群组聊天 结论 引言 随着实时通信技术的快速发展,聊天应用在现代We…...

基于Matlab的车牌识别停车场出入库计时计费管理系统(含GUI界面)【W6】
简介: 在当今城市化进程加快的环境下,停车管理成为了一个日益重要和复杂的问题。城市中的停车资源有限,如何高效利用和管理这些资源,不仅关乎市民出行便利性,也涉及到城市交通拥堵、环境污染等诸多问题的解决。 传统的…...

大众点评js逆向过程(未完)
相关链接 1、控制流平坦化进行AST 解析 AST网址 2、JS进制转换(Function.prototype.call) 1、断点调试mtgsig参数 这里mtgsig已经被拼到url中 2、进入后mtgsig已经计算完, ir he(this[b(4326)], !1), 就是加密函数 
web前端如何设置单元格:深入解析与实用技巧
web前端如何设置单元格:深入解析与实用技巧 在web前端开发中,设置单元格是一个常见且重要的任务。无论是构建数据表格、表单还是其他界面元素,都需要对单元格进行精确的设置和样式调整。那么,web前端究竟如何设置单元格呢&#x…...

龙迅LT9611UXC 2 PORT MIPIDSI/CSI转HDMI 2.1,支持音频IIS/SPDIF输入,支持标准4K60HZ输出
龙迅LT9611UXC描述: LT9611UXC是一个高性能的MIPI DSI/CSI到HDMI2.0转换器。MIPI DSI/CSI输入具有可配置的单端口或双端口,1高速时钟通道和1~4高速数据通道,最大2Gbps/通道,可支持高达16Gbps的总带宽。LT9611UXC支持突发模式DSI视…...

红黑树(C++)
文章目录 写在前面1. 红黑树的概念及性质1. 1 红黑树的概念1. 2 红黑树的性质 2. 红黑树节点的定义3. 红黑树的插入3.1 按照二叉搜索的树规则插入新节点3.2 检测新节点插入后,红黑树的性质是否造到破坏 4.红黑树的删除5.红黑树的验证6.源码 写在前面 在上篇文章中&…...
PyCharm设置不默认打开上次的项目
第一步 第二步 第三步 测试...
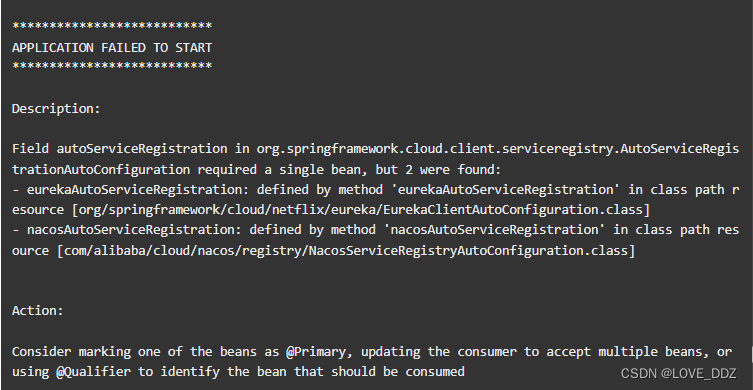
Eureka到Nacos迁移实战:解决配置冲突与启动异常
问题:Eureka到Nacos迁移实战:解决配置冲突与启动异常 在进行微服务架构升级,特别是注册中心从Eureka转向Nacos的过程中,我遇到了一个典型的技术挑战。目标是为了减少因配置变更导致的服务重启频率,我决定拥抱Nacos以其…...

k8s 小技巧: 查看 Pod 上运行的容器
目录 1. 示例 Pod 的定义文件2. kubectl describe pod(推荐)3. kubectl get pod3.1 json 格式3.2 yaml 格式 4. 其他操作 1. 示例 Pod 的定义文件 # 文章中所用 pod 的 yaml 定义文件, multi-container.yaml apiVersion: v1 kind: Pod metad…...

【Git】基础操作
初识Git 版本控制的方式: 集中式版本控制工具:版本库是集中存放在中央服务器的,team里每个人work时从中央服务器下载代码,是必须联网才能工作,局域网或者互联网。个人修改之后要提交到中央版本库 例如:SVM和…...
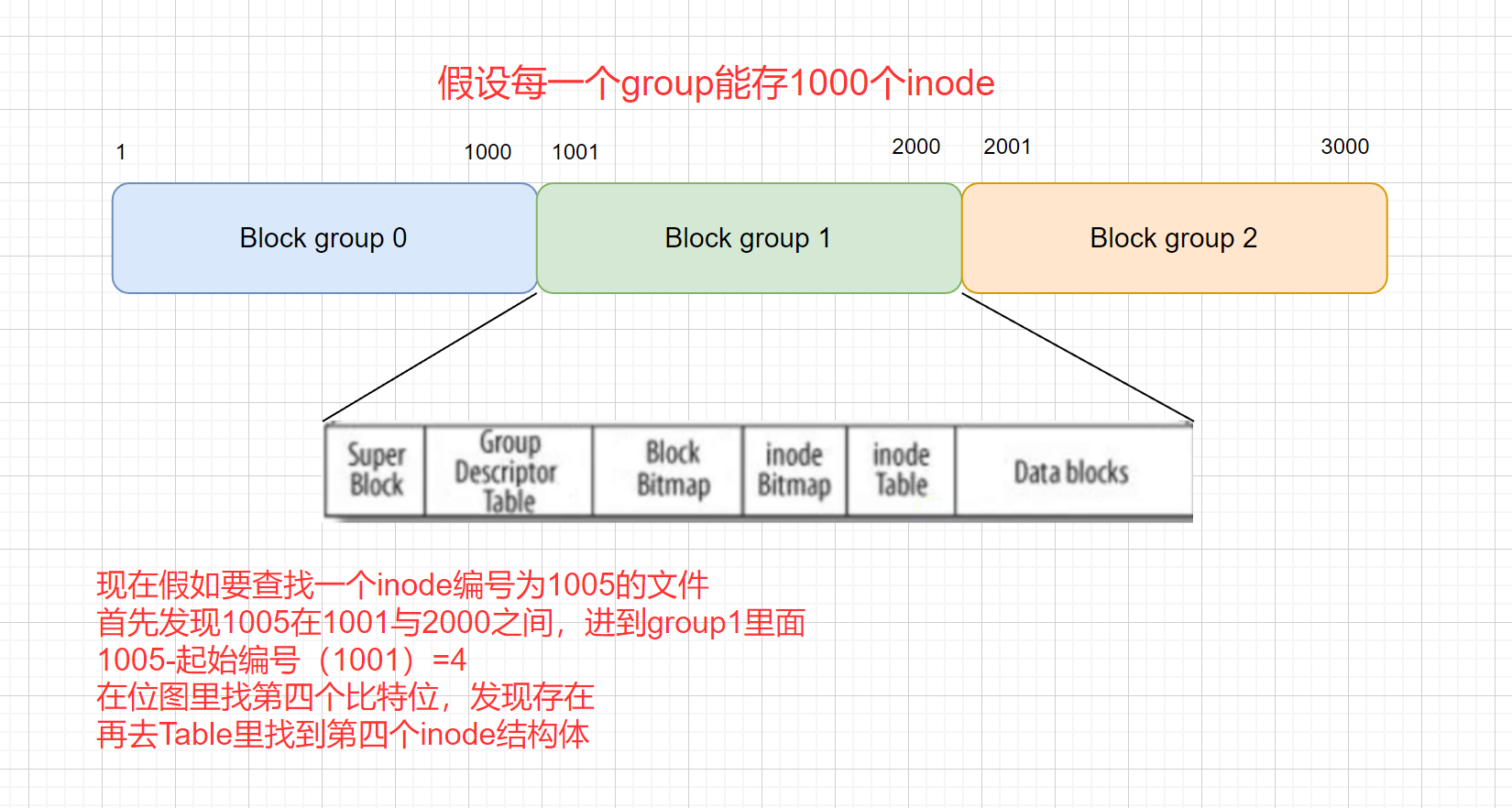
Linux:基础IO(二.缓冲区、模拟一下缓冲区、详细讲解文件系统)
上次介绍了:Linux:基础IO(一.C语言文件接口与系统调用、默认打开的文件流、详解文件描述符与dup2系统调用) 文章目录 1.缓冲区1.1概念1.2作用与意义 2.语言级别的缓冲区2.1刷新策略2.2具体在哪里2.3支持格式化 3.自己来模拟一下缓…...

事件传播机制 与 责任链模式
1、基本概念 责任链模式(Chain of Responsibility Pattern)是一种行为型设计模式,将请求沿着处理链传递,直到有一个对象能够处理为止。 2、实现的模块有: Handler(处理者):定义一个…...
uniapp 展示地图,并获取当前位置信息(精确位置)
使用uniapp 提供的map标签 <map :keymapIndex class"container" :latitude"latitude" :longitude"longitude" ></map> 页面初始化的时候,获取当前的位置信息 created() {let that thisuni.getLocation({type: gcj02…...
)
Autosar实践——诊断配置(DaVinci Configuration)
文章目录 一、制作诊断数据库文件(cdd文件)二、导入诊断数据库文件并修复模块生成的问题三、创建SWC CS接口Service Ports四、创建Service Runnable五、关联SWC和DCM/DEM模块六、RTE代码编写22服务2E服务31服务DTC Set/Get关联文章列表: Autosar-软件架构 Autosar诊断-简介和…...
植物大战僵尸杂交版全新版v2.1解决全屏问题
文章目录 🚋一、植物大战僵尸杂交版❤️1. 游戏介绍💥2. 如何下载《植物大战僵尸杂交版》 🚀二、解决最新2.1版的全屏问题🌈三、画质增强以及减少闪退 🚋一、植物大战僵尸杂交版 《植物大战僵尸杂交版》是一款在原版《…...

【code-server】Code-Server 安装部署
Code-Server 安装部署 1.环境准备 可以参考 https://coder.com/docs/code-server/install code-server的安装流程进行安装,主机环境是 Centos7 建议使用 docker 方式进行安装,可能会出现如下报错,需要升级 GNC 的版本,由于影响较…...

博客摘录「 YOLOv5模型剪枝压缩」2024年5月11日
添加L1正则来约束BN层系数 语义边缘检测和语义分割的关系调研结果为,语义信息可以用来增强语义分割的效果,也有一定的优点和采用理由,但此类论文的数量并不是很多,语义分割的多数方法还是使用深度学习直接做像素分类。在对比两者…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...
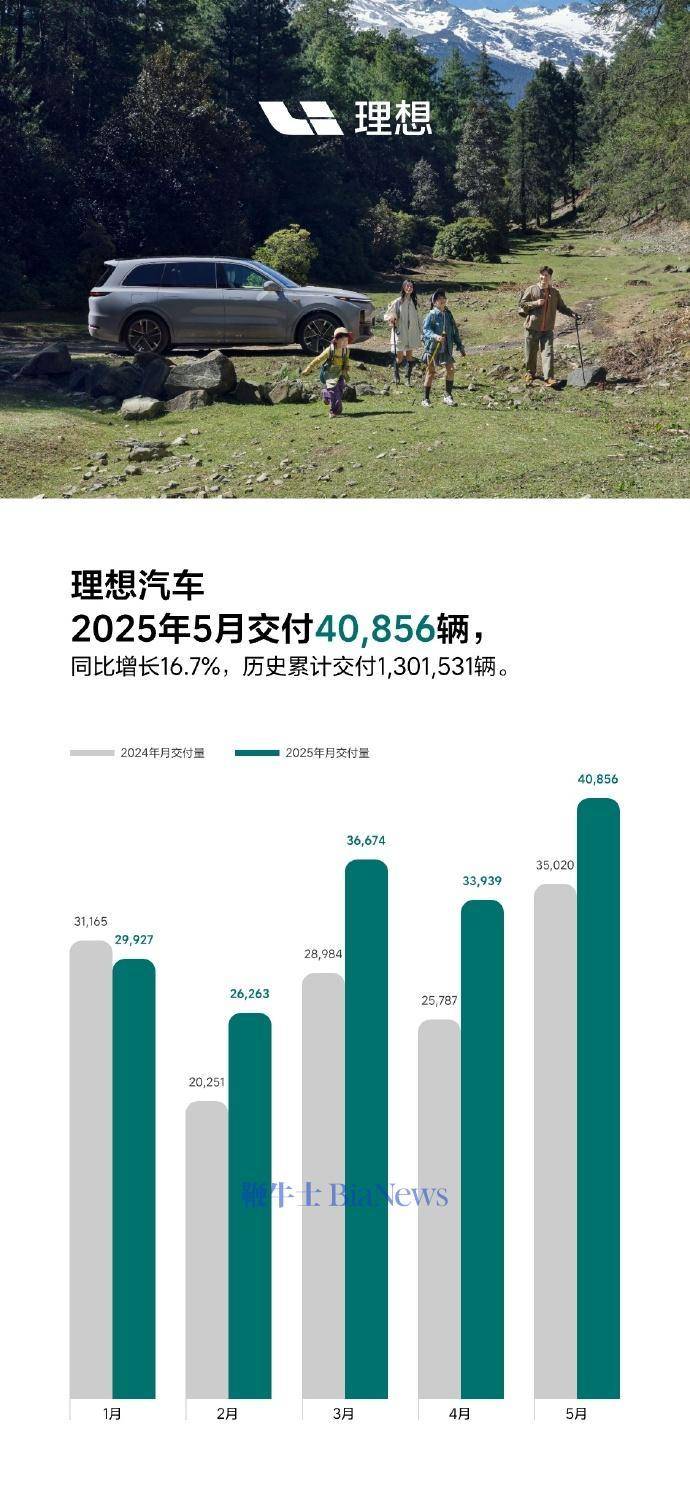
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...

