[二分枚举]特殊密码锁
描述
有一种特殊的二进制密码锁,由n个相连的按钮组成(n<30),按钮有凹/凸两种状态,用手按按钮会改变其状态。
然而让人头疼的是,当你按一个按钮时,跟它相邻的两个按钮状态也会反转。当然,如果你按的是最左或者最右边的按钮,该按钮只会影响到跟它相邻的一个按钮。
当前密码锁状态已知,需要解决的问题是,你至少需要按多少次按钮,才能将密码锁转变为所期望的目标状态。
输入
两行,给出两个由0、1组成的等长字符串,表示当前/目标密码锁状态,其中0代表凹,1代表凸。
输出
至少需要进行的按按钮操作次数,如果无法实现转变,则输出impossible。
样例输入
011 000
样例输出
1
解题分析
二进制序列,按了其中一个数可以让其和其旁边的一个或者两个数取反。
其实这道题的限制条件也很容易发现,关键就在于一个分类讨论,那就是第一个按钮开始的一个确定序列。什么意思?如果前面一个按钮按与不按的状态确定了,那么后续的按钮按与不按的状态也都确定了,我们只需要枚举第一个按钮的状态即可。这个又可以联想到一个15*15方格的画家图画板的问题,或者说是点灯问题,这也是很经典的。
我们枚举第一个按钮的状态,如果二者第一个数不同,我们要想改变第一个数的状态就只有按第一个按钮或者说按第二个按钮。如果我们选择了按第一个按钮,那么后续能够影响第二个按钮状态的就只有第三个按钮了,如果不按第一个按钮,我们就得按第二个按钮,然后我们同样地也可以发现能影响第二个按钮的就只有第三个按钮了,以此类推。
代码实现
#include <iostream>
#include <cmath>
#include <iomanip>
#include <string>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <map>
#include <set>
#include <unordered_map>
#include <unordered_set>
#include <list>
#include <bitset>
using namespace std;void press(string &s,int i){int l=s.size();if(i==0){s[i]=(s[i]=='1'?'0':'1');s[i+1]=(s[i+1]=='1'?'0':'1');}else if(i==l-1){s[i]=(s[i]=='1'?'0':'1');s[i-1]=(s[i-1]=='1'?'0':'1');}else{s[i]=(s[i]=='1'?'0':'1');s[i-1]=(s[i-1]=='1'?'0':'1');s[i+1]=(s[i+1]=='1'?'0':'1');}
}int main(){string cur,des;int len;int c=0;int res=1e9;cin>>cur>>des;len=cur.size();//分类讨论,第一个位置按或者不按,总共只有这两种情况//之后的每个位置都因为第一个位置按或者不按而确定string cur1=cur;press(cur,0);c++;for(int i=1;i<len;i++){if(cur[i-1]==des[i-1]){continue;}else{press(cur,i);c++;}} if(cur==des){res=min(res,c);}c=0;for(int i=1;i<len;i++){if(cur1[i-1]==des[i-1]){continue;}else{press(cur1,i);c++;}}if(cur1==des){res=min(res,c);}if(res==1e9){cout<<"impossible"<<endl;}else{cout<<res<<endl;}return 0;
}相关文章:

[二分枚举]特殊密码锁
描述 有一种特殊的二进制密码锁,由n个相连的按钮组成(n<30),按钮有凹/凸两种状态,用手按按钮会改变其状态。 然而让人头疼的是,当你按一个按钮时,跟它相邻的两个按钮状态也会反转。当然&am…...

MT1434 找数字
题目 输入一个字符串(包含26个英文字母大小写及 . 空格,不含其他字符),把其中连续的数字作为一个整数,依次存放到一个数组中,输出这些整数的和。 格式 输入格式 输入字符串 输出格式 输出整型 样例1 输入: a12…...

2024年6月四六级考试复盘
一、考试情况 1.1四级考试情况 听力:一开始没有进入状态。总共对了9道。7.1*37.1*314.2*3 8.2 新闻听力:3/7 长对话:3/8 讲座/讲话:3/10 阅读:3.55*7 7.1*8 14.2 * 7 181.05 选词填空:保守估计7/1…...

join和left join性能比较
1、join和left join性能比较(AI生成) 在MySQL中,JOIN和LEFT JOIN的效率并不是绝对的,它们之间的性能差异取决于多种因素,如表的大小、使用的索引、查询的复杂性等。 一般来说: 如果两个表之间的连接条件能…...

Qt正则表达式
需求:对输入的内容进行限制 只能以字母或下划线开始不能以数字开始 不能有中文 字母,数字,下划线混合使用 QRegExp rx("^[A-Za-z_][A-Za-z0-9_]*$");QRegExpValidator validator(rx);QLineEdit edit;edit.setValidator(&va…...
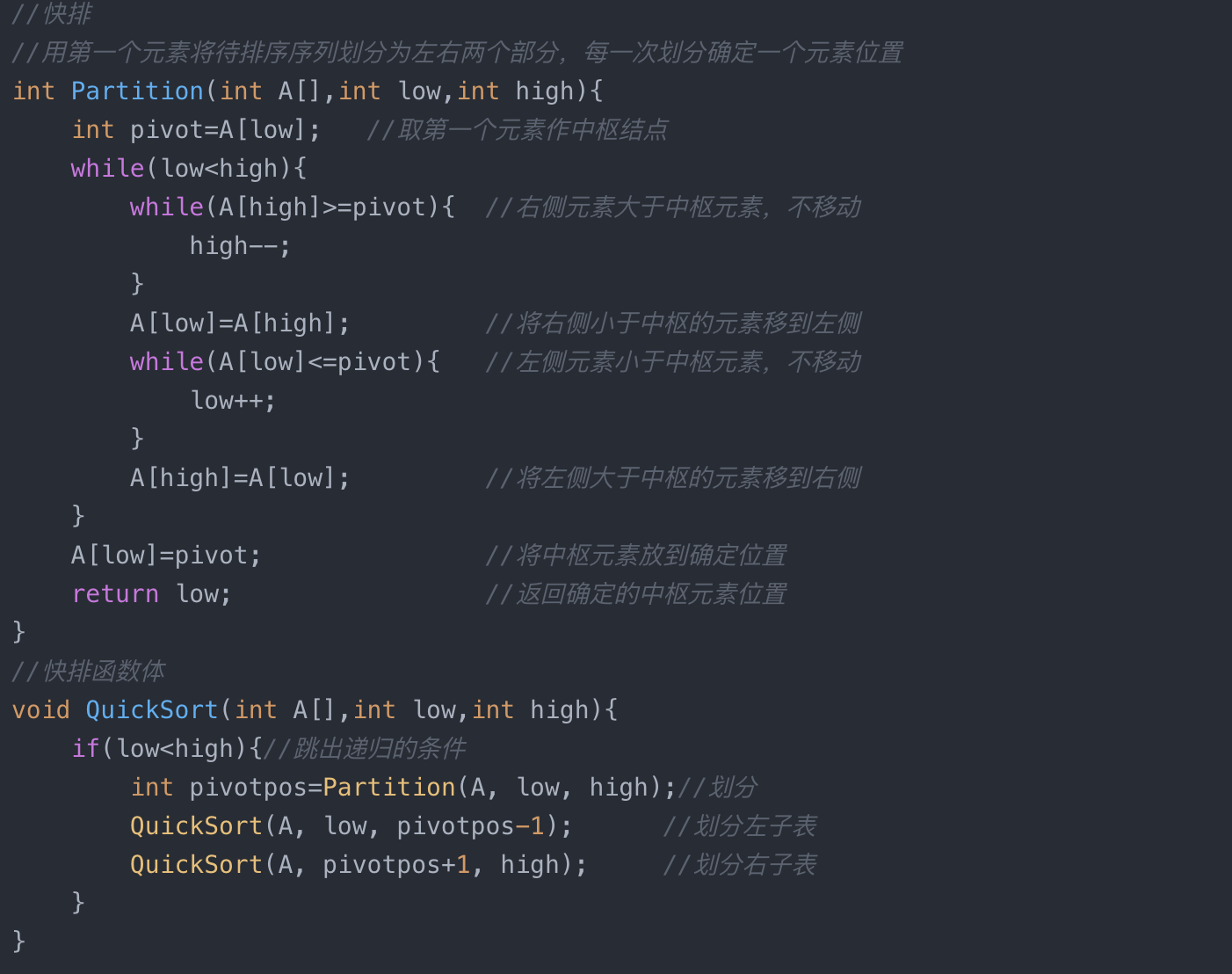
排序-快排算法对数组进行排序
目录 一、问题描述 二、解题思路 1.初始化 2.将右侧小于基准元素移到左边 3.将左侧大于基准元素移到右边 4.重复执行上面的操作 5.对分好的左、右分区再次执行分区操作 6.最终排序结果 三、代码实现 四、刷题链接 一、问题描述 二、解题思路 快排算法实现数组排序&am…...

flink学习-容错机制
checkpoint(检查点) 在flink中最重要的容错机制,就是checkpoint机制,使用checkpoint可以将之前某个时间点的所有的状态进行保存,这个存档就是checkpoint。 检查点的保存 周期性存储保存,间隔时间可以由用…...

InfluxDB技术分享
InfluxDB是一个开源的时间序列数据库,它被设计用来处理高速写入和查询大量的时间序列数据。以下是一份关于“InfluxDB在Java开发中的使用”的三十分钟技术分享内容概要: 1. 引言 (2分钟) 介绍时间序列数据和时间序列数据库的概念。引入InfluxDB的特点和…...
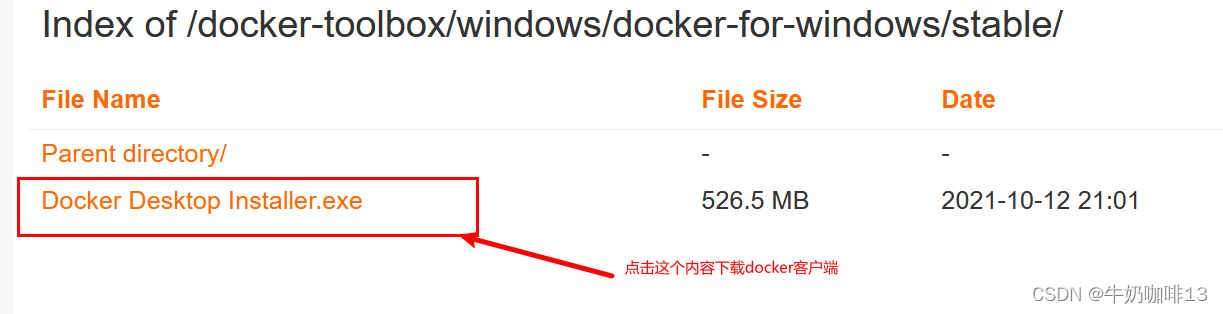
Windows10安装配置Docker客户端和WSL2与Hyper-V虚拟机
一、需求说明 需要在Windows系统中安装配置Docker的客户端,方便直接管理配置docker镜像容器内容。 二、Windows10安装Docker客户端步骤 2.1、下载安装Docker客户端 对于Windows 10以下的用户,推荐使用Docker Toolbox Windows安装文件:http://mirrors.aliyun.com/docker-…...
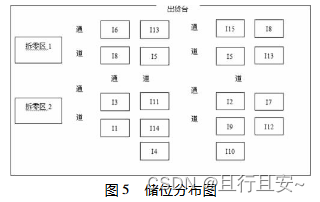
EIQ-ABC 分析法在配送中心储位分配中的应用
配送中心运作效率的高低主要取决于仓储业务流程的作业效率,在配送作业流程中,储位分配的是否合理性成为影响配送运作效率的重要因素。为实现储位的合理分配,提出通过对订单信息的分析,并应用 EIQ-ABC 分析法,以此实现缩…...
【安装笔记-20240613-Linux-在 OpenWrt 的 LuCI界面支持命令行调试】
安装笔记-系列文章目录 安装笔记-20240613-Linux-在 OpenWrt 的 LuCI界面支持命令行调试 文章目录 安装笔记-系列文章目录安装笔记-20240613-Linux-在 OpenWrt 的 LuCI界面支持命令行调试 前言一、软件介绍名称:ttyd主页官方介绍特点 二、安装步骤测试版本…...
_基础部分)
React小记(一)_基础部分
1、项目搭建与结构 2、类组件和函数组件 主要区别:1、函数组件没有生命周期2、函数组件没有this指向3、函数组件没有状态4、函数组件通过hooks实现各种操作5、props在函数的第一个参数接收6、函数体相当于类组件的render函数import React from reactfunction App()…...

40、基于深度学习的线性预测设计(matlab)
1、原理及流程 深度学习的线性预测是一种利用深度神经网络模型进行线性回归预测的方法。其设计原理主要基于神经网络的层次化特性,利用多层感知器(MLP)等模型进行特征学习和非线性变换,从而提高线性预测的准确性。 设计流程如下…...

【初体验 threejs】【学习】【笔记】hello,正方体 3!
前言 为了满足工作需求,我已着手学习 Three.js,并决定详细记录这一学习过程。在此旅程中,如果出现理解偏差或有其他更佳的学习方法,请大家不吝赐教,在评论区给予指正或分享您的宝贵建议,我将不胜感激。 项…...
第04章:IDEA的安装与使用
第04章:随堂复习与企业真题(IDEA安装与使用) 一、随堂复习 1. IDEA的认识 IDEA(集成功能强大、符合人体工程学(设置人性化))Eclipse 2. IDEA的下载、安装、卸载 卸载:使用控制面板进行卸载,…...

[原创][Delphi多线程]使用TMonitor, TEvent和TQueue配合实现TThreadQueue的经典使用案例.
[简介] 常用网名: 猪头三 出生日期: 1981.XX.XX QQ: 643439947 个人网站: 80x86汇编小站 https://www.x86asm.org 编程生涯: 2001年~至今[共22年] 职业生涯: 20年 开发语言: C/C、80x86ASM、PHP、Perl、Objective-C、Object Pascal、C#、Python 开发工具: Visual Studio、Delph…...
6.12ctf练习
[西湖论剑 2022]Node Magical Login 源码在这里:GitHub - CTF-Archives/2022-xhlj-web-node_magical_login: A web challenge in 2022 西湖论剑大赛打开 打开环境是个登录框,先进行了扫描和抓包都没有看见什么有价值的东西,看源码 大致连接…...

海豚调度异常处理: 使用 arthas 在内存中删除启动失败的工作流
💡 本系列文章是 DolphinScheduler 由浅入深的教程,涵盖搭建、二开迭代、核心原理解读、运维和管理等一系列内容。适用于想对 DolphinScheduler了解或想要加深理解的读者。祝开卷有益。大数据学习指南 大家好,我是小陶,DolphinSch…...
 和 readAll() 有什么关联和联系)
在Qt中,QSerialPort::write(data) 和 readAll() 有什么关联和联系
在Qt中,QSerialPort::write(data) 和 readAll() 是与串行通信相关的两个不同的函数,它们属于 QSerialPort 类。这两个函数在串行通信中扮演不同的角色,但它们之间存在一定的联系: QSerialPort::write(data) 这个函数用于将数据发…...
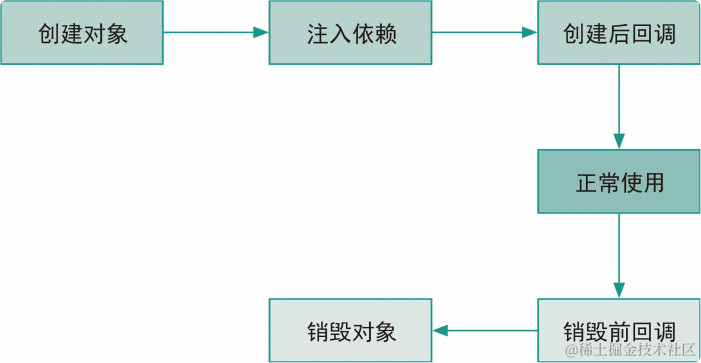
第 2 章:Spring Framework 中的 IoC 容器
控制反转(Inversion of Control,IoC)与 面向切面编程(Aspect Oriented Programming,AOP)是 Spring Framework 中最重要的两个概念,本章会着重介绍前者,内容包括 IoC 容器以及容器中 …...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
