[鹤城杯 2021]BabyRSA
题目:
from Crypto.Util.number import getPrime, bytes_to_long
from secret import flagp = getPrime(1024)
q = getPrime(1024)
n = p * q
e = 65537
hint1 = p >> 724
hint2 = q % (2 ** 265)
ct = pow(bytes_to_long(flag), e, n)
print(hint1)
print(hint2)
print(n)
print(ct)hint1= 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
hint2= 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n= 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
ct= 19073695285772829730103928222962723784199491145730661021332365516942301513989932980896145664842527253998170902799883262567366661277268801440634319694884564820420852947935710798269700777126717746701065483129644585829522353341718916661536894041337878440111845645200627940640539279744348235772441988748977191513786620459922039153862250137904894008551515928486867493608757307981955335488977402307933930592035163126858060189156114410872337004784951228340994743202032248681976932591575016798640429231399974090325134545852080425047146251781339862753527319093938929691759486362536986249207187765947926921267520150073408188188
解题分析: 因此根据题目中给出的p高300位和q低265位,n=pq => n=p0q0(mod 2265)可得p低265位 p0=nq0-1(mod 2265) 题目中q0= q%(2265)=hint2 => q0-1= inverse_mod(q0,2265) 则p低265位p0=n*inverse_mod(q0,2265)(mod 2265) 则p的高300位和低265位之和为: pbar=ph+pl=(p1<<724) + n*inverse_mod(q0,2265)(mod 2265) p中间的459位通过copperSmith求解 由于构造f=pbar+x*2265无解,尝试对2265抬高2^6(即抬高64)进行爆破 则 f需要加上i*2265,其中i in range(64) 所以在copperSmith构造中,f表达式中间项为x*64*2265,对应small_roots参数X=2453
sage:
#sage
p1 = 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
q0 = 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
p0=n*invert(q0,2^265)%(2^265)
pbar=(p1<<724)+p0PR.<x> = PolynomialRing(Zmod(n))
for i in range(64):f=pbar+x*(2^265)*64 + i*(2^265)f=f.monic()pp=f.small_roots(X=2^453,beta=0.4)if(pp):print("pp[0]=",pp[0])print("i=",i)breakp=pbar+pp[0]*64*(2^265)+ i*(2^265)
print("p=",p)python:
#python
from Cryptodome.Util.number import *
import libnum
from gmpy2 import gmpy2hint1 = 1514296530850131082973956029074258536069144071110652176122006763622293335057110441067910479
hint2 = 40812438243894343296354573724131194431453023461572200856406939246297219541329623
n = 21815431662065695412834116602474344081782093119269423403335882867255834302242945742413692949886248581138784199165404321893594820375775454774521554409598568793217997859258282700084148322905405227238617443766062207618899209593375881728671746850745598576485323702483634599597393910908142659231071532803602701147251570567032402848145462183405098097523810358199597631612616833723150146418889589492395974359466777040500971885443881359700735149623177757865032984744576285054725506299888069904106805731600019058631951255795316571242969336763938805465676269140733371287244624066632153110685509892188900004952700111937292221969
ct = 19073695285772829730103928222962723784199491145730661021332365516942301513989932980896145664842527253998170902799883262567366661277268801440634319694884564820420852947935710798269700777126717746701065483129644585829522353341718916661536894041337878440111845645200627940640539279744348235772441988748977191513786620459922039153862250137904894008551515928486867493608757307981955335488977402307933930592035163126858060189156114410872337004784951228340994743202032248681976932591575016798640429231399974090325134545852080425047146251781339862753527319093938929691759486362536986249207187765947926921267520150073408188188
e = 65537
p=133637329398256221348922087205912367118213472434713498908220867690672019569057789598459580146410501473689139466275052698529257254973211963162087316149628000798221014338373126500646873612341158676084318494058522014519669302359038980726479317742766438142835169562422371156257894374341629012755597863752154328407
q=n//p
phi_n=(p-1)*(q-1)
d = gmpy2.invert(e,phi_n)
m = pow(ct,d,n)
print(long_to_bytes(m))相关文章:

[鹤城杯 2021]BabyRSA
题目: from Crypto.Util.number import getPrime, bytes_to_long from secret import flagp getPrime(1024) q getPrime(1024) n p * q e 65537 hint1 p >> 724 hint2 q % (2 ** 265) ct pow(bytes_to_long(flag), e, n) print(hint1) print(hint2) p…...
)
西安市工业倍增引导基金子基金申报条件流程和材料程序指南(2024年)
一、基本情况 产业投资基金是以产业发展为首要目标,围绕经济社会发展规划和产业发展政策,发挥“有效市场”作用,支持重点领域、重点产业、重点区域(如:全市六大支柱产业、五大新兴产业领域成熟期重点规模以上企业以及“…...

微型丝杆的耐用性和延长使用寿命的关键因素!
无论是机械设备,还是精密传动元件,高精度微型丝杆是各种机械设备中不可或缺的重要组件。它的精度和耐用性直接影响着工作效率和产品品质,在工业技术不断进步的情况下,对微型丝杆的性能要求也越来越高,如何提升微型丝杆…...
音频文件下载后,如何轻松转换格式?
在我们日常的数字生活中,下载各种音频文件是司空见惯的事情。然而,有时候我们可能需要将这些音频文件转换为不同的格式,以适应不同的设备或编辑需求。无论您是希望将下载的音频文件转换为通用的MP3格式,还是需要将其转换为高保真的…...
Intel平台,13600KF+3060Ti,虚拟机安装macOS 14(2024年6月)
距离上次装macOS虚拟机已经有一段时间了,macOS系统现在大版本升级的速度也是越来越快了,由于Office只支持最新三个版本的macOS,所以现在保底也得安装macOS 12了,我这次是用macOS 14做实验,13和12的安装方式和macOS 14一…...
Cookie、Session、Token的关系和区别
关系 Session与Cookie:Session通常依赖于Cookie来工作。当服务器为客户端创建一个Session时,它会在服务器上存储与客户端相关的信息,并将一个唯一的SessionID通过Cookie发送给客户端。客户端在后续的请求中会携带这个Cookie(包含…...
Windows 11 中安装 Docker Desktop 并安装镜像
本该主要介绍在 Windows 11 中安装 Docker Desktop 时的一些准备工作,以及该如何下载和安装,然后分别使用管理界面和 Docker 命令安装两个镜像。 一、准备工作 在 Windows 11 中安装 Docker Desktop 前,需要做一些准备。打开 【Windows 功能…...

深入剖析Java线程池之“newWorkStealingPool“
1. 概述 newWorkStealingPool 是Java 8中引入的一个新型线程池,它基于ForkJoinPool实现,并采用了“工作窃取”(Work-Stealing)算法。这种线程池特别适用于可并行化且计算密集型的任务,能够充分利用多核CPU资源,提高任务执行效率。 2. 工作窃取算法(Work-Stealing Algor…...
《跟我一起学“网络安全”》——安全设备
安全设备 一、安全设备–IDS IDS入侵检测 (1)什么是入侵检测: 入侵检测系统(intrusion detection system,简称“IDS”)是一种对网络传输进行即时监视,在发现可疑传输时发出警报或者采取主动反应措施的网络安全设备。…...

猜测Tomcat如何实现WebSocket协议
一、WebSocket协议的实现 (一)WebSocket是官方的协议接口标准。 (二)如果一门编程语言可以网络连接和并发,就能创建一种WebSocket实现。 (三)同一种编程语言,有不同的协议实现版本和框架。 二、Tomcat实现 在Tomcat容器中实现了对应的WebSocket版本&am…...
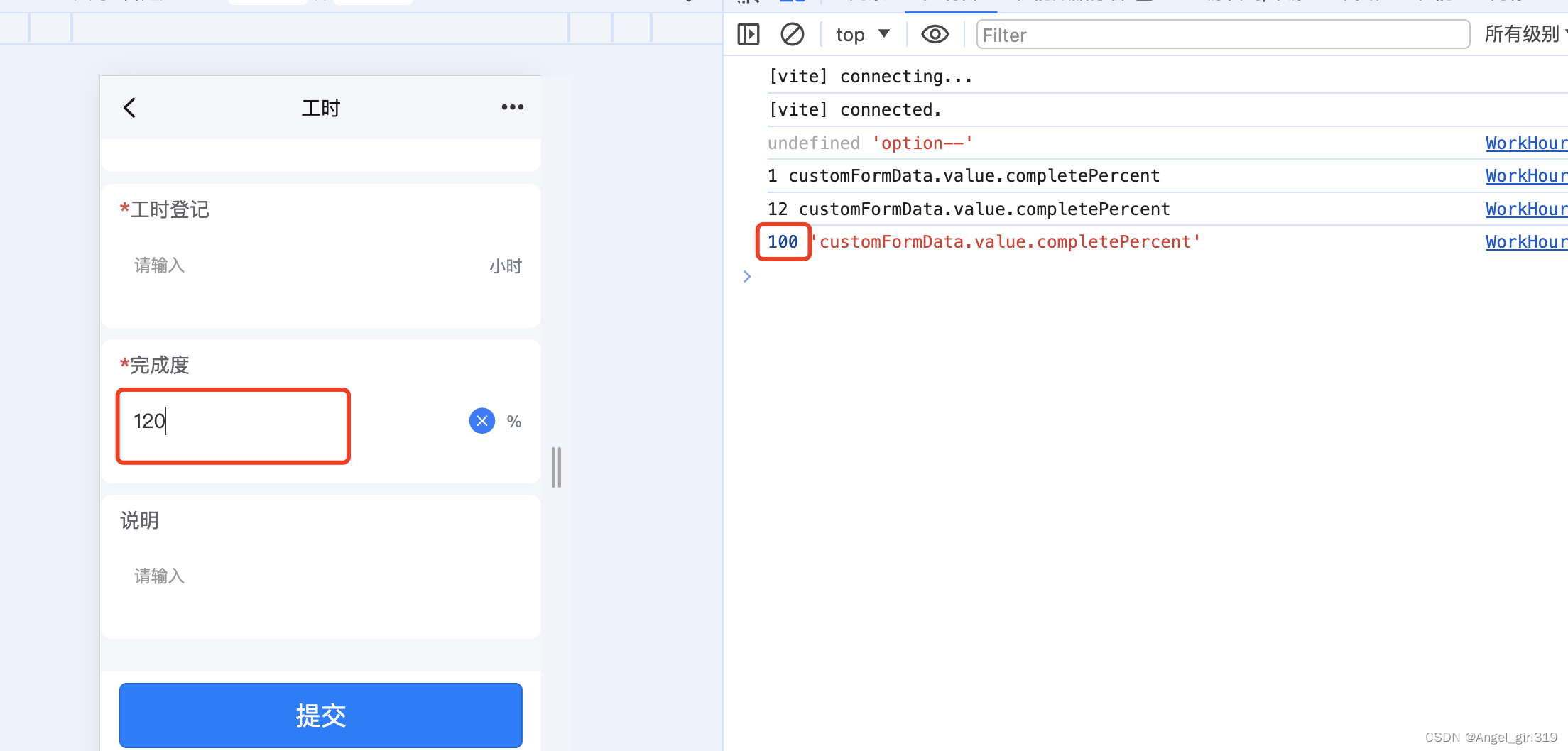
uniApp @input事件更改输入框值,值改变了但是页面没更新新的值
<uni-easyinputtype"text"trim"all":inputBorder"false"v-model"customFormData.completePercent"input"(val) > completeOnInput(val)"placeholder"请输入" /> function completeOnInput(val) {let num…...

两行css 实现瀑布流
html <ul ><li><a href"" ><img src"05094532gc6w.jpg" alt"111" /><p>传奇</p></a></li><li><a href"" ><img src"05094532gc6w.jpg" alt"111"…...

Centos7.9部署单节点K8S环境
Centos7.9部署单节点K8S环境 通过Centos extras镜像源安装K8S环境,优点是方便快捷,缺点是版本较低,安装后的版本为1.5.2。 1. 准备工作 关闭selinux [rootlocalhost ~]# cat /etc/selinux/config# This file controls the state of SELin…...

【CV】stable diffusion初步理解
来自gpt-4o Stable diffusion 和DALLE的关系 Stable Diffusion 和 DALL-E 都是生成图像的人工智能模型,但它们有不同的开发背景和技术实现。 Stable Diffusion: 开发者: 由Stability AI开发,并与CompVis和LAION等组织合作。技术: 基于扩散模型…...

足底筋膜炎最好的恢复办法
足底筋膜炎是一种由足底筋膜受到炎症刺激而引起的疼痛和不适的疾病。其典型症状主要包括: 1、足底疼痛:这是足底筋膜炎最常见的症状。疼痛通常位于足跟部位,患者可能感到刺痛或灼热感。尤其在早晨起床或长时间站立后,这种疼痛感会…...

Fiddler抓包工具介绍
下载 下载:Web Debugging Proxy and Troubleshooting Tools|Fiddler 进去要填一个表 汉化版 百度网盘 请输入提取码 提取码:xq9t 下载过附件之后分别把两个文件 点开fiddler就ok了 配置https fiddler要想抓到https包(解密的),点击tools->options勾选三个对…...
知乎号开始运营了,宣传一波
知乎号开始发布一些小说、散文还有诗歌了,欢迎大家多来关注 知乎链接:姜亚轲 每篇小说都改编成网易云音乐,文章中也有链接,我做的词,Suno编曲和演唱,欢迎大家来听听...

Go 基础丨切片 slice
1. 底层 runtime/slice.go type slice struct {array unsafe.Pointer // 指向底层数组len int // 切片元素数量cap int // 底层数组容量 }reflect/value.go type SliceHeader struct {Data uintptrLen intCap int }2. 创建 根据数组创建 s : arr[0:3]字面…...

哪个牌子充电宝好用?精选四大热门款充电宝品牌!公认好用
在当今快节奏的生活中,充电宝已经成为了我们日常生活中不可或缺的数码伴侣。无论是旅行、出差还是日常通勤,拥有一款好用的充电宝,能够确保我们的手机、平板等设备随时保持充足电量。然而,市场上充电宝品牌繁多,如何选…...
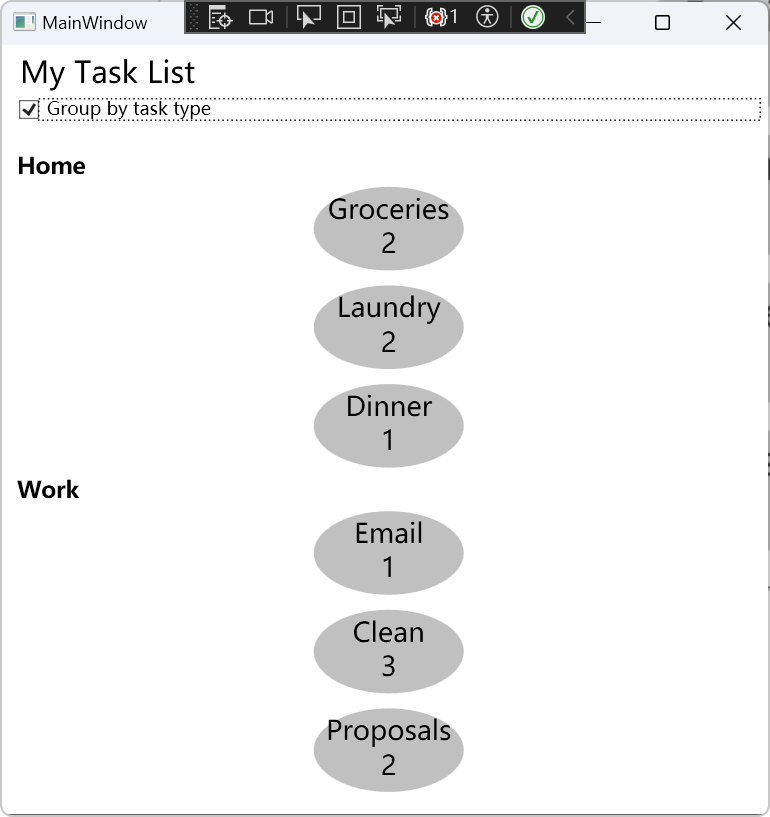
WPF/C#:如何将数据分组显示
WPF Samples中的示例 在WPF Samples中有一个关于Grouping的Demo。 该Demo结构如下: MainWindow.xaml如下: <Window x:Class"Grouping.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x&q…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...
