算法题解记录29+++全排列(百日筑基)
一、题目描述
题目难度:中等
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
提示:
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同
二、解题准备
第一,题意
不解释
第二,基本操作
涉及到数组的遍历,List的增加,可能还有List的删除。
第三,基础原理
对于回溯算法,从大的方面讲,题解一般涉及递归(迭代解法过于复杂)。
从小的方面讲,可能会关系到将题目、解题过程转化为解空间树。
这棵解空间树,一般都是满多叉树(可能会用剪枝算法,降低运行时间)
一般来说,这棵解空间树,有这样的特点:
它的叶子节点是真正的题解。
它的其它节点,可以理解为解题过程。
因此,学会遍历多叉树,是解题的基础算法,链接如下:
多叉树遍历算法
三、解题思路
针对该题,我们先手动地解题。
对于数组【a,b,c】
它的排列有以下可能:
第一,如果先选择a,
那么,余下【b,c】进行选择。
紧接着1,如果选择b,余下c进行选择
有答案1为【a,b,c】
紧接着1,如果选择c,余下b选择
有答案2为【a,c,b】
第二,如果先选择b,
那么,余下【a,c】进行选择。
紧接着2,如果选择a,余下c,
有答案3为【b,a,c】
其它同理
我们可以发现,这颗多叉树,从空节点开始,每一层都会减少一个节点,如下图:

问题1:这不是满多叉树
想必你也发现了,随着层次减少,上一层总比下一层多出一个节点。
这是因为,在全排列中,如果某个位置使用了a,那么,其它的位置就不能使用a。
根据全排列的性质,我们可以得到这么个规律(假设length是输入数组的长度):
第一层:有length个节点【忽略,根节点】
第二层:有length-1个节点
……
第length层:有1个节点。此时,这个节点是叶子节点。【也就是我们需要的答案】
问题2:这棵多叉树难以遍历
这棵多叉树虽然结构鲜明,但明显是个刺头,难以下手。
假如,我们使用一个boolean数组,来标记哪个节点被访问,然后根据访问情况,进行遍历判断。
也许可行,不过我没写出来,主要问题出现在:
// 随机拿一个未访问的节点
// 使boolean数组为true
访问。
// 设置boolean数组为false
这几个步骤中,有2大问题:
第一,随机访问节点,很可能会访问到上一次的节点,这会造成答案重复。
第二,我们不能确定,究竟要访问多少次。【如果用nums的长度为标准,我们会发现,下一层节点,又只有上一层-1个。】
四、解题难点分析
难点如上所示。(我的观点)
难点定义:在数据处理的过程中,数据结构在不断变化。
最开始,有length个节点。
第二层,剩下length-1个。
……
到最后一层,只有1个了。
我们没法用统一的结构,处理这个问题。
A1思考:递归函数的解决结构
我们学习过二叉树的DFS深度优先遍历,以及斐波那契的递归函数。
其实可以发现,它有递归调用递归的过程。
// 斐波那契
return feibo(n-1) + feibo(n-2);
然而,这两个方案处理的数据结构,是一致的。
虽然斐波那契每次往前回调2次,但是,至始至终,处理的数据量都是2。
二叉树同理,每次处理的都是左子、右子两个节点。
在本题的多叉树中,每次处理的节点在依次减少。
B2解决方案:双层递归函数
我们定义函数A,它提供一个方案:
A处理数据量为len的数组,依次从数组中拿出一个数,然后将此数移出数组,递归调用A函数,处理len-1的数组。
也就是说,A处理的对象是固定的:
只处理数据量为len的数组,其它的情况,交给它的子递归函数。
并且,A处理的结构,每次会按要求减少,直到符合叶子节点,然后返回答案。
代码在下方,在此仅解释。
C3难点:确定参数
A的参数比较难以确定,这属于是回溯法的特点之一。
我在此介绍一种思路:
3个关键词:结果集、答案集、输入集
结果集:求解过程中的临时变量,到达叶子节点时,就是一个答案。
答案集:存储所有答案的全局或局部变量。
输入集:变化的数据结构。
另外的参数,需要看题目情况,动态地变化。
D4难点:变化的输入集
由上可知,输入集在不断变化。
如果现在输入集为【a,b,c】
在选择后,剩下【b,c】
如果采用数组的结构,每次新生成一个数组,然后把【b,c】存储到数组,接着再递归调用。
可以发现,这会占用比较大的内存空间,而且数组复制的时间复杂度也不小。
因此,我们可以采用List链表,每次添加一个数,或者删除一个数,这样使用的内存空间会大大减少。
五、代码
class Solution {public List<List<Integer>> permute(int[] nums) {// 答案集List<List<Integer>> res = new ArrayList<List<Integer>>();// 输入集List<Integer> damn = new ArrayList<>();// 将数组转化为List,节省内存for(int i:nums){damn.add(i);}dfs_n(new ArrayList<>(), res, damn);return res;}// data是结果集,临时答案private void dfs_n(List<Integer> data, List<List<Integer>> res, List<Integer> damn){// size为0,就是叶子节点的下一层,该返回了if(damn.size() == 0){res.add(new ArrayList<>(data));return;}// 每次访问输入集的长度for(int i=0; i<damn.size(); i++){// tem仍要用于回溯,所以用个tem存储int tem = damn.get(i);// 结果集添加,输入集移除data.add(tem);damn.remove(i);// 调用子递归函数dfs_n(data, res, damn);// 结果集移除,输入集恢复data.remove(data.size()-1);damn.add(i, tem);}}
}
六、结语
以上内容即我想分享的关于力扣热题29的一些知识。
我是蚊子码农,如有补充,欢迎在评论区留言。个人也是初学者,知识体系可能没有那么完善,希望各位多多指正,谢谢大家。
相关文章:

算法题解记录29+++全排列(百日筑基)
一、题目描述 题目难度:中等 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示…...

苹果AI功能,AI训练数据缺乏,SD3推出,MJ6推出新特性
更多信息: https://agifun.love 智源社区 2024智源大会议程公开丨大模型前沿探索 2024年6月14日-15日,第6届北京智源大会将以线下与线上结合的形式召开,线下会场设在中关村国家自主创新示范区会议中心。2024智源大会再次以全球视野&#x…...

超越中心化:Web3如何塑造未来数字生态
随着技术的不断发展,人们对于网络和数字生态的期望也在不断提升。传统的中心化互联网模式虽然带来了便利,但也暴露出了诸多问题,比如数据滥用、信息泄露、权力集中等。在这样的背景下,Web3技术应运而生,旨在打破传统中…...
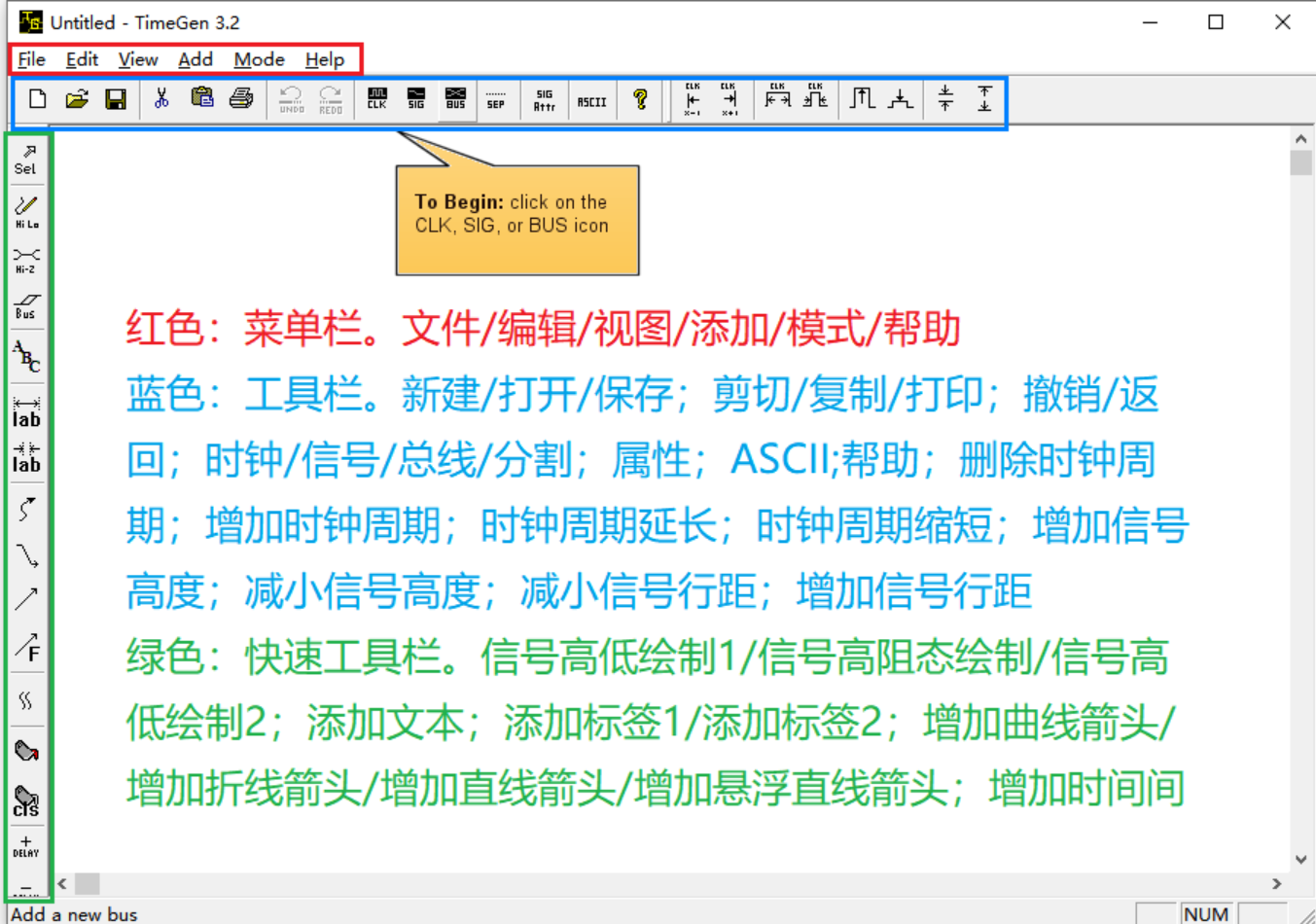
【ic-tool】timegen使用
一、前言 TimeGen是一个用于时序波形编辑的CAD工具,它允许数字设计工程师快速有效地绘制数字时序图。TimeGen时序图可以很容易地导出到其他窗口程序,如microsoftword,用于编写设计规范。可直接从官网下载TimeGEN软件:TimeGen Pro…...
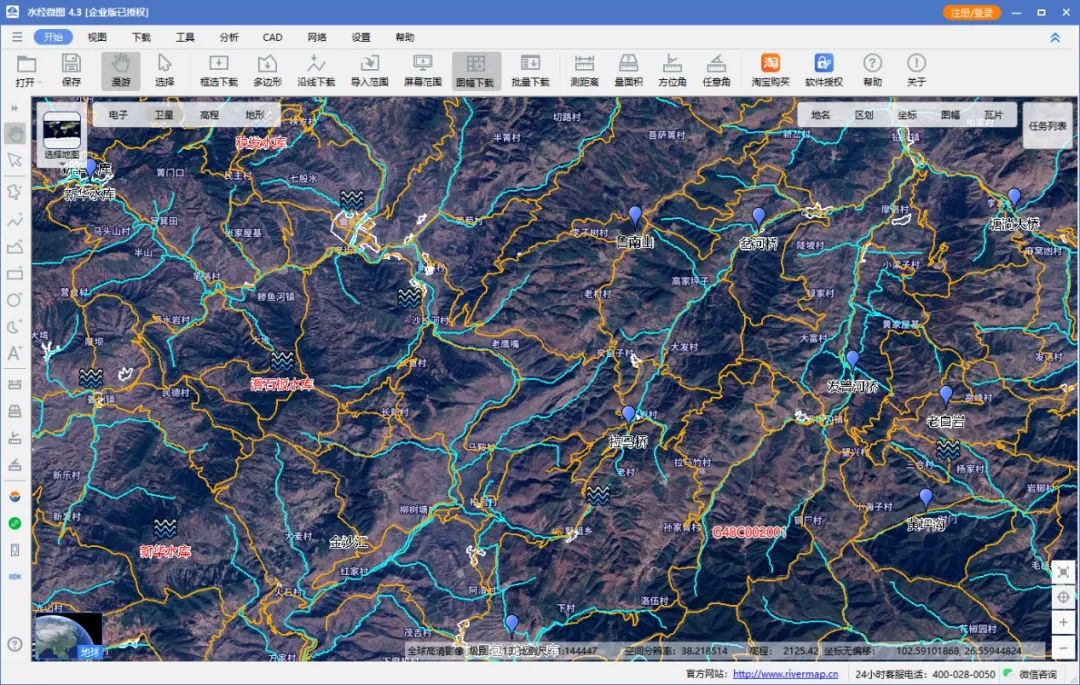
1:25万基础电子地图(云南版)
我们在《50幅1:25万基础电子地图(四川版)》一文中,为你分享过四川的50幅基础电子地图。 现在我们再为你分享云南的1:25万基础电子地图,你可以在文末查看该数据的领取方法。 基础电子地图云南版 下载后可以看到该数据…...
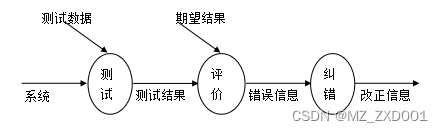
springboot宠物领养系统-计算机毕业设计源码07863
摘 要 21世纪的今天,随着社会的不断发展与进步,人们对于信息科学化的认识,已由低层次向高层次发展,由原来的感性认识向理性认识提高,管理工作的重要性已逐渐被人们所认识,科学化的管理,使信息存…...

牛客热题:最长回文子串
📟作者主页:慢热的陕西人 🌴专栏链接:力扣刷题日记 📣欢迎各位大佬👍点赞🔥关注🚓收藏,🍉留言 文章目录 牛客热题:最长回文子串题目链接方法一&am…...

如何访问寄存器
标题 方式一:对地址进行宏定义方式二:用结构体封装寄存器 访问寄存器是CPU执行程序的基础,每种CPU架构都有其特定的寄存器集合和访问方式。 方式一:对地址进行宏定义 #define GPIOA_BASE ((unsigned int)0x48000000) #define GPI…...

苍穹外卖笔记-18-修改密码、bug记录
文章目录 1 修改密码1.1 需求分析和设计1.2 代码实现1.2.1 admin/EmployeeController1.2.2 EmployeeService1.2.3 EmployeeServiceImpl 1.3 功能测试 2 bug记录 1 修改密码 完结的时候发现还有一个接口未实现。这里补充 1.1 需求分析和设计 产品原型: 业务规则&am…...

java如何截取字符串
如果想在一个字符串中截取一段字符,形成新的字符,那么在java中途需要用到substring语句 substring的语法格式是 str.substring(beginindex,endindex) 其中str是字符串 beginindex是起始索引,endindex是结束索引 截取的字符串包含起始索引…...

虚拟淘宝-Virtual-Taobao论文解读(AAAI2019)
目录 1 论文简介 2 文章的主要贡献 3 文章技术的简要说明 4 技术的详细说明 4.1 GAN-SD:生成客户特征 4.2 MAIL:生成交互过程 4.3 ANC:动规范约束 5 实验设定及结果 6 结论 7 参考 1 论文简介 南京大学LAMDA团队的侍竞成、俞扬等…...
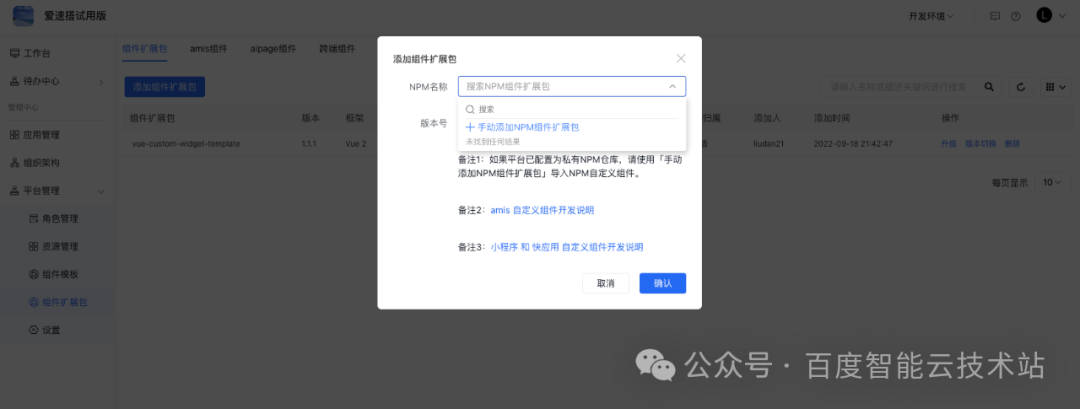
低代码组件扩展方案在复杂业务场景下的设计与实践
组件是爱速搭的前端页面可视化模块的核心能力之一,它将前端研发人员从无休止的页面样式微调和分辨率兼容工作中解放了出来。 目前,爱速搭通过内置的上百种功能组件(120),基本可以覆盖大部分中后台页面的可视化设计场景…...

震撼科技界的GPT-4o发布首日即遭“越狱破防”
前言 本文主要解读分析OpenAI最新推出的大型模型GPT-4o可能存在的越狱风险。 5 月14 日凌晨的科技圈再一次被OpenAI轰动,其发布的最新大模型GPT-4o,能力横跨语音、文本和视觉,这一成果无疑再次巩固了OpenAI在人工智能领域的领先地位。 然而…...
保护密码安全,探讨密码加盐及其在Go语言中的实现
介绍 在当今数字化时代,个人隐私和数据安全成为了人们关注的焦点之一。随着网络犯罪的不断增加,用户的密码安全性变得尤为重要。密码加盐作为一种常见的安全措施,被广泛应用于密码存储和认证系统中。本文将深入探讨密码加盐的概念、重要性以…...
Sqoop学习详细介绍!!
一、Sqoop介绍 Sqoop是一款开源的工具,主要用于在Hadoop(HDFS/Hive/HBase)与传统的数据库(mysql、postgresql...)间进行数据的传递,可以将一个关系型数据库(例如 : MySQL ,Oracle ,Postgres等)中的数据导进到Hadoop的H…...
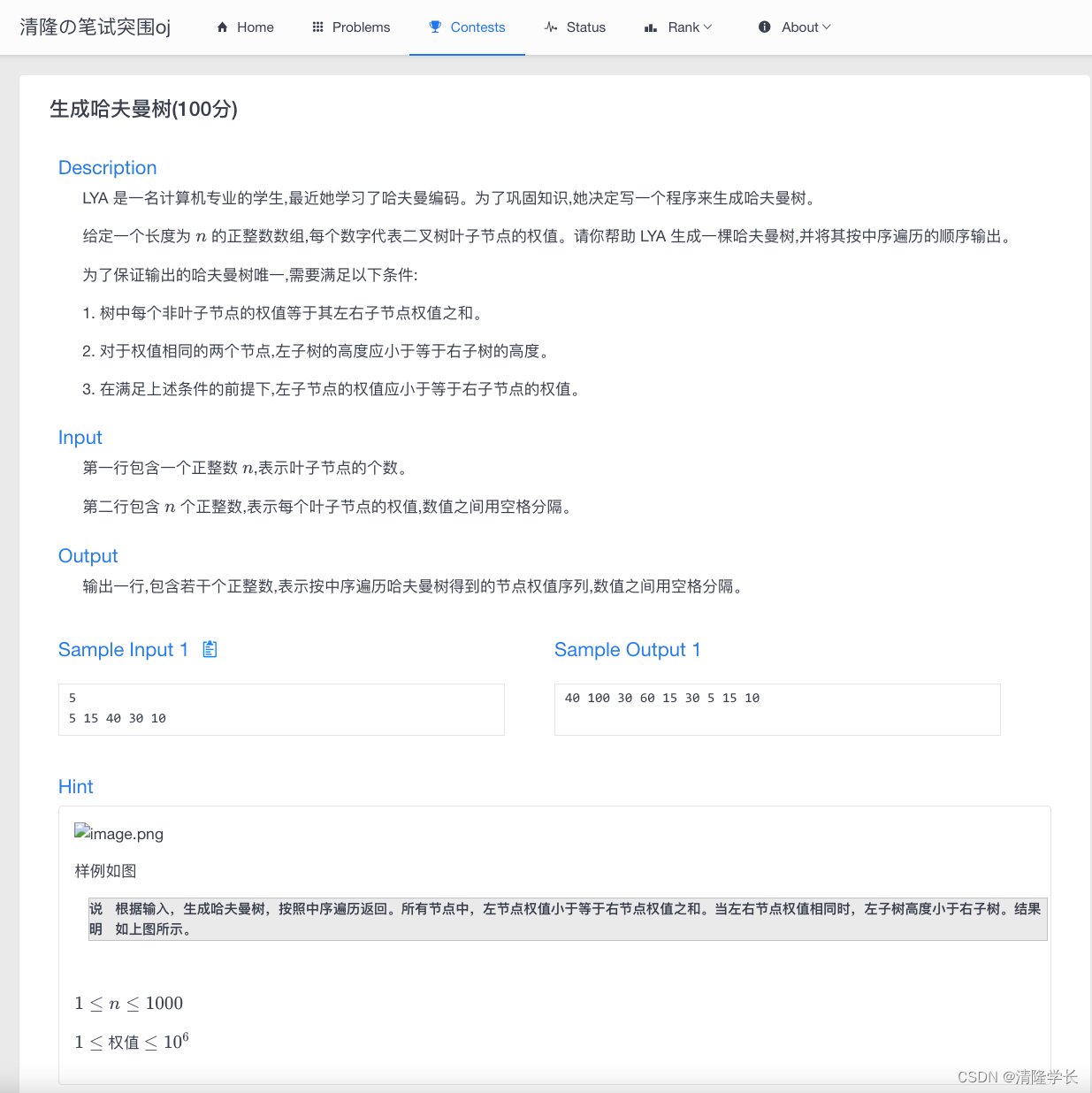
【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 生成哈夫曼树(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 📎在线评测链接 生成哈夫曼树(100分) 🌍 评测功能需要订阅专栏后私信联系清…...
ctfshow web 单身杯
web签到 <?phperror_reporting(0); highlight_file(__FILE__);$file $_POST[file];if(isset($file)){if(strrev($file)$file){ //翻转函数include $file;}}要进行反转并且包含文件用data协议 自己写不好写可以用函数帮你翻转 <?php $adata:text/plain,<?eval(…...

天锐绿盾加密软件,它的适用范围是什么?
天锐绿盾数据防泄密软件的适用范围广泛,主要可以归纳为以下几点: 行业适用性: 适用于各个行业,包括但不限于制造业、设计行业、软件开发、金融服务等,特别是对数据安全性要求较高的行业。企业规模与类型: 适…...

mysql面试题 Day2
1 长文本如何存储? 可以使用Text存储 TINYTEXT(255长度) TEXT(65535) MEDIUMTEXT(int最大值16M) LONGTEXT(long最大值4G) 2 大段文本存储如何设计表结构? 分表存储 分表后多段存储 3 大段文本查找时如何建立索引࿱…...
Excel加密怎么设置?这5个方法不容错过!(2024总结)
Excel加密怎么设置?如何不让别人未经允许查看我的excel文件?如果您也有这些疑问,那么千万不要错过本篇文章了。今天小编将向大家分享excel加密的5个简单方法,保证任何人都可以轻松掌握!毫无疑问的是,为Exce…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
