过拟合与正则化
Location Beijing
过拟合
对于一个模型 A A A,解向量空间为 θ \theta θ,误差函数用式1表示
J ( θ ) = J a c c = [ y θ ( x ) − y ] 2 (1) J(\theta)=J_{acc}=[y_\theta(x)-y]^2\tag{1} J(θ)=Jacc=[yθ(x)−y]2(1)
首先我们考虑用模型 A A A拟合下图Fig. 1这些点(数据集)

首先用一个模型去拟合这个曲线 y = a + b x + c x 2 + d x 3 y=a+bx+cx^2+dx^3 y=a+bx+cx2+dx3,可得如下图Fig. 2
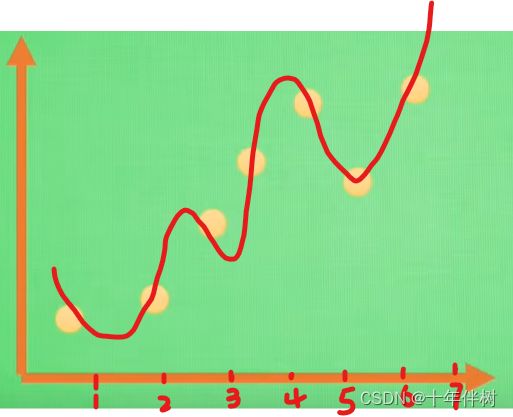
简直完美,因为误差 J ( θ ) J(\theta) J(θ)=0。然而当我预测 x = 4 x=4 x=4的函数值时,发现预测值比真实值稍微大一丢丢,虽然感觉不对劲但是还可以接受;但当我预测 x = 20 x=20 x=20的函数值时,发现预测值大的离谱。
具体原因可以从上图Fig. 2看出,模型认为数据集中的点所有 x x x及其对应的 y y y都是百分百对应的,过分相信了数据集的准确性,忽略了数据集的误差。实际上可以看出,比如上图Fig. 2数据集中的 x = 2 x=2 x=2的点对应的函数值大概是 y = 2 y=2 y=2,然而数据集却把这一项标注成了 y = 1 y=1 y=1。模型A太牛逼直接把带误差的数据集学通透了。
这里也可以看出为什么说过拟合的表现是 J ( θ ) J(\theta) J(θ)很小,但是预测新数据的能力很差,因为过拟合的模型太复杂,另外数据集标注太烂。
正则化
接下来看用正则化解决这个问题。
具体方法式在 J ( θ ) J(\theta) J(θ)后面加一个正则化项,对于加入L1正则化的误差函数如公式2,加入L2正则化项的误差函数如公式3
J L 1 ( θ ) = J a c c + L 1 = [ y θ ( x ) − y ] 2 + [ ∣ θ 1 ∣ + ∣ θ 2 ∣ . . ] (2) J_{L1}(\theta)=J_{acc}+L_1=[y_\theta(x)-y]^2+[|\theta_1|+|\theta_2|..]\tag{2} JL1(θ)=Jacc+L1=[yθ(x)−y]2+[∣θ1∣+∣θ2∣..](2)
J L 2 ( θ ) = J a c c + L 2 = [ y θ ( x ) − y ] 2 + [ θ 1 2 + θ 2 2 + . . ] (3) J_{L2}(\theta)=J_{acc}+L_2=[y_\theta(x)-y]^2+[\theta_1^2+\theta_2^2+..]\tag{3} JL2(θ)=Jacc+L2=[yθ(x)−y]2+[θ12+θ22+..](3)
从公式2、3可以看出所谓正则化就是想以“牺牲”一些准确率的代价,来避免模型的复杂度。这里“牺牲”加引号的原因可以从第一章看出,这点损失的“准确率”事实上是象征着数据集的不准确性。让模型更有泛化能力。
至于为什么说L1正则化更容易得到稀疏的向量解空间,可以通过图Fig. 3看出,假设 θ \theta θ是一个二维向量,包含两个元素{ θ 1 \theta_1 θ1, θ 2 \theta_2 θ2}。(一个模型肯定不止两个参数,这里举两个参数的例子是比较好画)
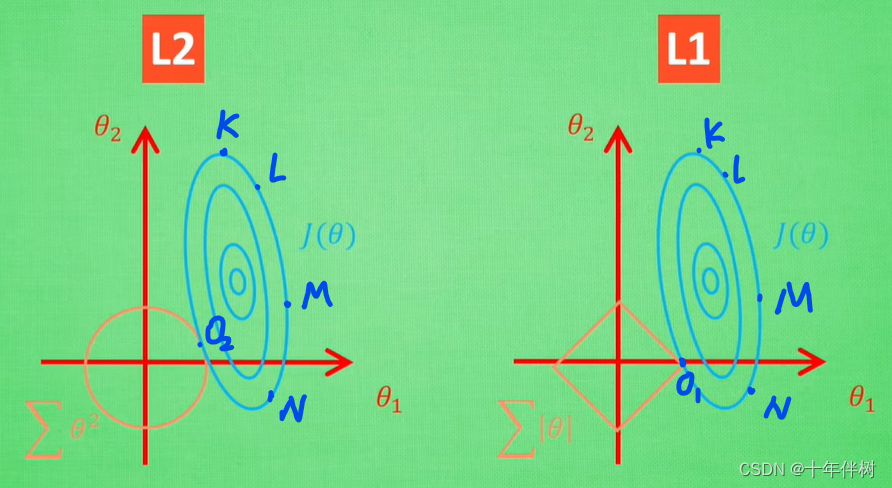
图Fig. 3中每个蓝色椭圆上的点表示不同的 θ \theta θ使 J ( θ ) J(\theta) J(θ)(注意不是 J a c c ( θ ) J_{acc}(\theta) Jacc(θ))相同的点。如点 K K K, L L L, M M M, N N N, O 2 O_2 O2是解空间 θ \theta θ使含L2正则化项的误差函数 J L 2 ( θ ) J_{L2}(\theta) JL2(θ)相同的点,这一批点中显然点 O 2 O_2 O2的L2正则化项最小;再比如点 K K K, L L L, M M M, N N N, O 1 O_1 O1是解空间 θ \theta θ使含L1正则化项的误差函数 J L 1 ( θ ) J_{L1}(\theta) JL1(θ)相同的点,这一批点中显然点 O 1 O_1 O1的L1正则化项最小。(从公式2、3可以看出,相同的 J ( θ ) J(\theta) J(θ),正则化项越小, J a c c ( θ ) J_{acc}(\theta) Jacc(θ)越大,所以尽量保留正则化较小的 θ \theta θ解)
从这里可以看出L1正则化更容易使正则化项最小的同时, J a c c ( θ ) J_{acc}(\theta) Jacc(θ)最大,而且还带来了一个效果,由于L1正则化尖尖的探出的部分,更容易使 θ \theta θ中的某一项为0,这就造成了L1正则化解空间的稀疏性。如果还想更稳妥,把这个正则化项改成非凸函数,特定情况下在成稀疏性的概率更大。
reference
[1] 莫烦Python 2017 什么是 L1 L2 正规化 正则化 Regularization (深度学习 deep learning)
相关文章:

过拟合与正则化
Location Beijing 过拟合 对于一个模型 A A A,解向量空间为 θ \theta θ,误差函数用式1表示 J ( θ ) J a c c [ y θ ( x ) − y ] 2 (1) J(\theta)J_{acc}[y_\theta(x)-y]^2\tag{1} J(θ)Jacc[yθ(x)−y]2(1) 首先我们考虑用模型 A A A拟合下…...

VMware挂载NAS存储异常处理
问题概述 由于非法关机或恢复,NFS存储可能会出现以下问题: 数据存储处于挂起状态或无法正常识别。虚拟机的配置文件或虚拟磁盘仍然注册在异常数据存储上。系统误认为有虚拟机在使用该数据存储。 问题对策 下面是详细的排查步骤和解决对策:…...

Redis 7.x 系列【4】命令手册
有道无术,术尚可求,有术无道,止于术。 本系列Redis 版本 7.2.5 源码地址:https://gitee.com/pearl-organization/study-redis-demo 文章目录 1. 说明2. 命令手册2.1 Generic2.2 数据类型2.2.1 String2.2.2 Hash2.2.3 List2.2.4 S…...

走进Elasticsearch
什么是ES 是一个分布式、RESTful风格的搜索和数据分析引擎 中文参考文档: 《Elasticsearch中文文档》 | Elasticsearch 技术论坛 elasticSearch官网: Functions and Operators | Elasticsearch Guide [7.11] | Elastic查询方式 Kibana查询(原…...

QT TCP服务器和客户端示例程序
下面是一个简单的 Qt TCP 服务器和客户端示例,演示了如何使用 vSetDriver、vSetListener 和 vTcpServerStart 函数。假设 vSetDriver 和 vSetListener 是你定义的自定义函数。 TCP 服务器部分 tcpserver.h #ifndef TCPSERVER_H #define TCPSERVER_H#include <QT…...
Xlua三方库Android编译出错解决办法
Xlua三方库Android编译出错解决办法 最近听老师的热更教程,讲到xlua编译android平台会报错,也是看了老师的博客,按照方法去解决,然而问题并没有解决。应该是因为代码更新或者版本不一样,在此简单记录一下解决过程。 参…...

美国犹他州立大学《Nature Geoscience》(IF=18)!揭示草本植物对土壤有机碳的重要贡献!
随着全球变暖的影响越来越显著,碳固定成为了一个备受关注的话题。在这个背景下,热带草原被认为是一个潜在的碳固定区域。然而,目前的研究主要关注于在热带草原中种植树木,以期望增加土壤有机碳含量。但是,热带草原中的…...

高考专业抉择计算机专业热度不减,兴趣、实力与挑战并存。
作为一名即将步入大学校门的高考生,我对于计算机相关专业是否仍是热门选择感到困惑。在过去几年里,计算机科学与技术、人工智能、网络安全、软件工程等专业一直备受追捧,吸引了无数学生。然而,随着市场竞争加剧和市场饱和度提高&a…...

Flask-RQ
Flask-RQ库教程 Flask-RQ 是一个用于在 Flask 应用中集成 RQ(Redis Queue)的扩展。RQ 是一个简单的 Python 库,用于将任务排入 Redis 队列并异步执行这些任务。这对于处理长时间运行的任务(如发送电子邮件、生成报告等࿰…...

LeetCode 58. 最后一个单词的长度
LeetCode 58. 最后一个单词的长度 你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。 单词 是指仅由字母组成、不包含任何空格字符的最大子字符串 示例 1: 输入:s “Hello World”…...
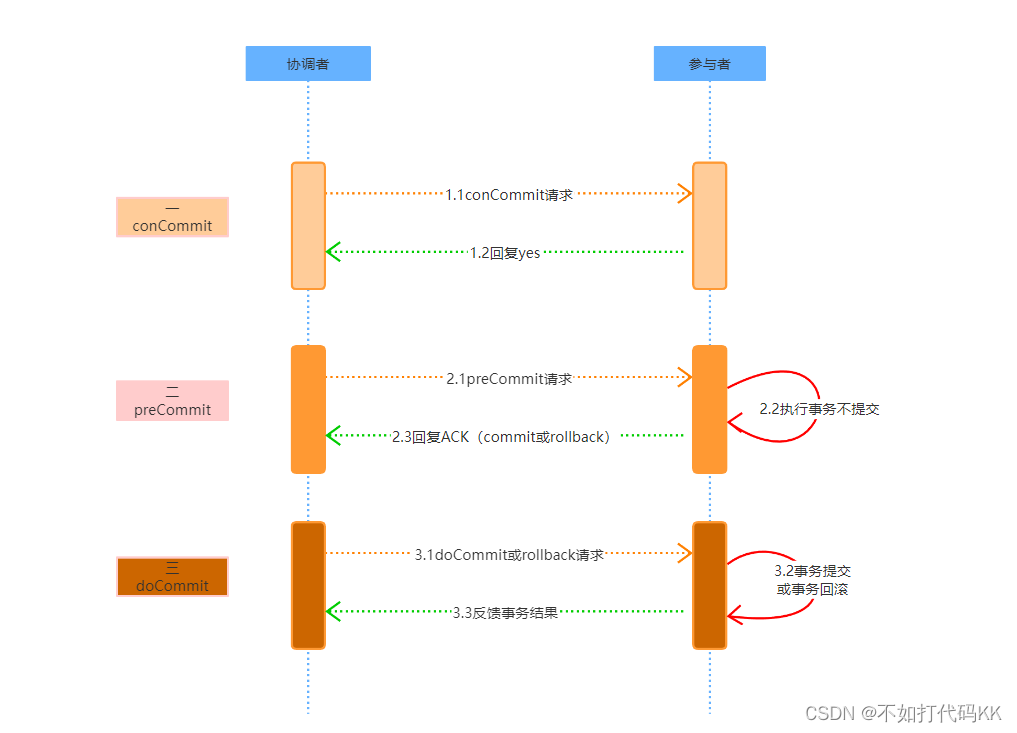
3阶段提交协议(3pc)
3阶段提交协议(3pc) 1 简介 三阶段提交协议是一个强一致、中心化的原子提交协议。解决了分布式事务、副本容错等分布式问题。其核心思想是将2PC的二阶段提交协议的“准备阶段”一分为二,形成了由CanCommit、PreCommit、DoCommit三个阶段组成…...

802.11中的各种帧
在无线网络中,802.11协议定义了三种类型的帧:管理帧(Management Frames)、控制帧(Control Frames)和数据帧(Data Frames)。每种类型的帧都有其特定的功能,帮助维护和管理…...

SAP PP学习笔记21 - 计划策略的Customize:策略组 > 策略 > 需求类型 > 需求类(消费区分,计划区分)
上面几章讲了MTS,MTO,ATO的计划策略。 本章来讲一下它的后台 Customize。 1,Customizeing:Planned Indep.Reqmts Management 这是配置计划策略的整个过程: - Requirements Type / Class 需求类型 / 需求类 - Plann…...
axure9设置组件自适应浏览器大小
问题:预览时不展示下方的滚动条 方法一:转化为动态面板 1.在页面上创建一个矩形 2.右键-转化为动态面板 3.双击进入动态面板设置 4.设置动态面板矩形的颜色 5.删除原来的矩形 6.关闭动态面板,点击预览 7.此时可以发现底部没有滚动条了 方法…...

示例:WPF中TreeView自定义TreeNode泛型绑定对象来实现级联勾选
一、目的:在绑定TreeView的功能中经常会遇到需要在树节点前增加勾选CheckBox框,勾选本节点的同时也要同步显示父节点和子节点状态 二、实现 三、环境 VS2022 四、示例 定义如下节点类 public partial class TreeNodeBase<T> : SelectBindable<…...

C++ explicit关键字的用法
在C中,explicit关键字用于构造函数和转换运算符,以防止隐式转换。它可以帮助我们避免意外的类型转换,从而提高代码的安全性和可读性。explicit关键字只能用于单参数构造函数和转换运算符。 使用explicit的场景 单参数构造函数: 当…...

51.Python-web框架-Django开始第一个应用的增删改查
目录 1.概述 2.创建应用 创建app01 在settings.py里引用app01 3.定义模型 在app01\models.py里创建模型 数据库迁移 4.创建视图 引用头 部门列表视图 部门添加视图 部门编辑视图 部门删除视图 5.创建Template 在app01下创建目录templates 部门列表模板depart.ht…...
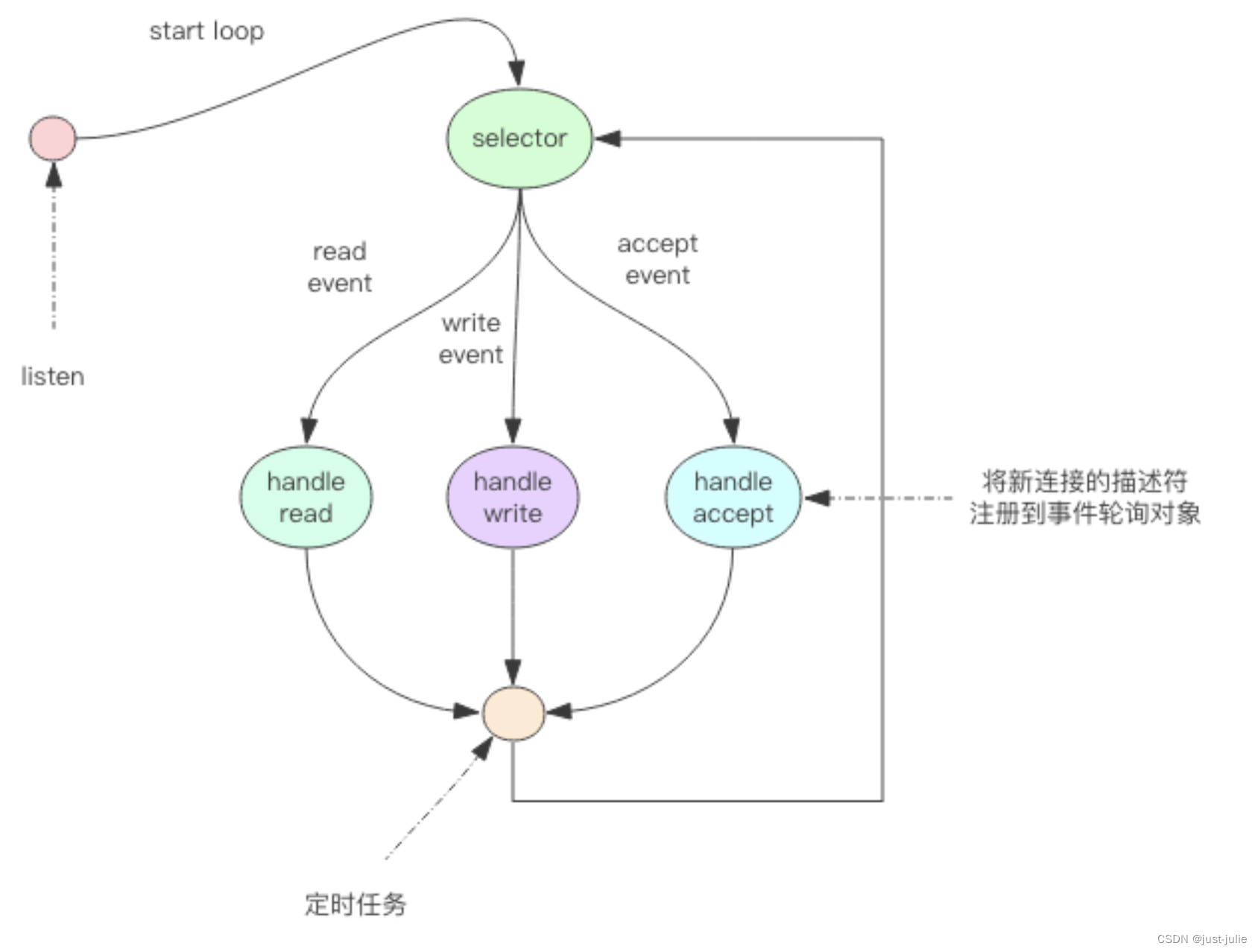
Redis之线程IO模型
引言 Redis是个单线程程序!这点必须铭记。除了Redis之外,Node.js也是单线程,Nginx也是单线程,但是他们都是服务器高性能的典范。 Redis单线程为什么能够这么快! 因为他所有的数据都在内存中,所有的运算都…...
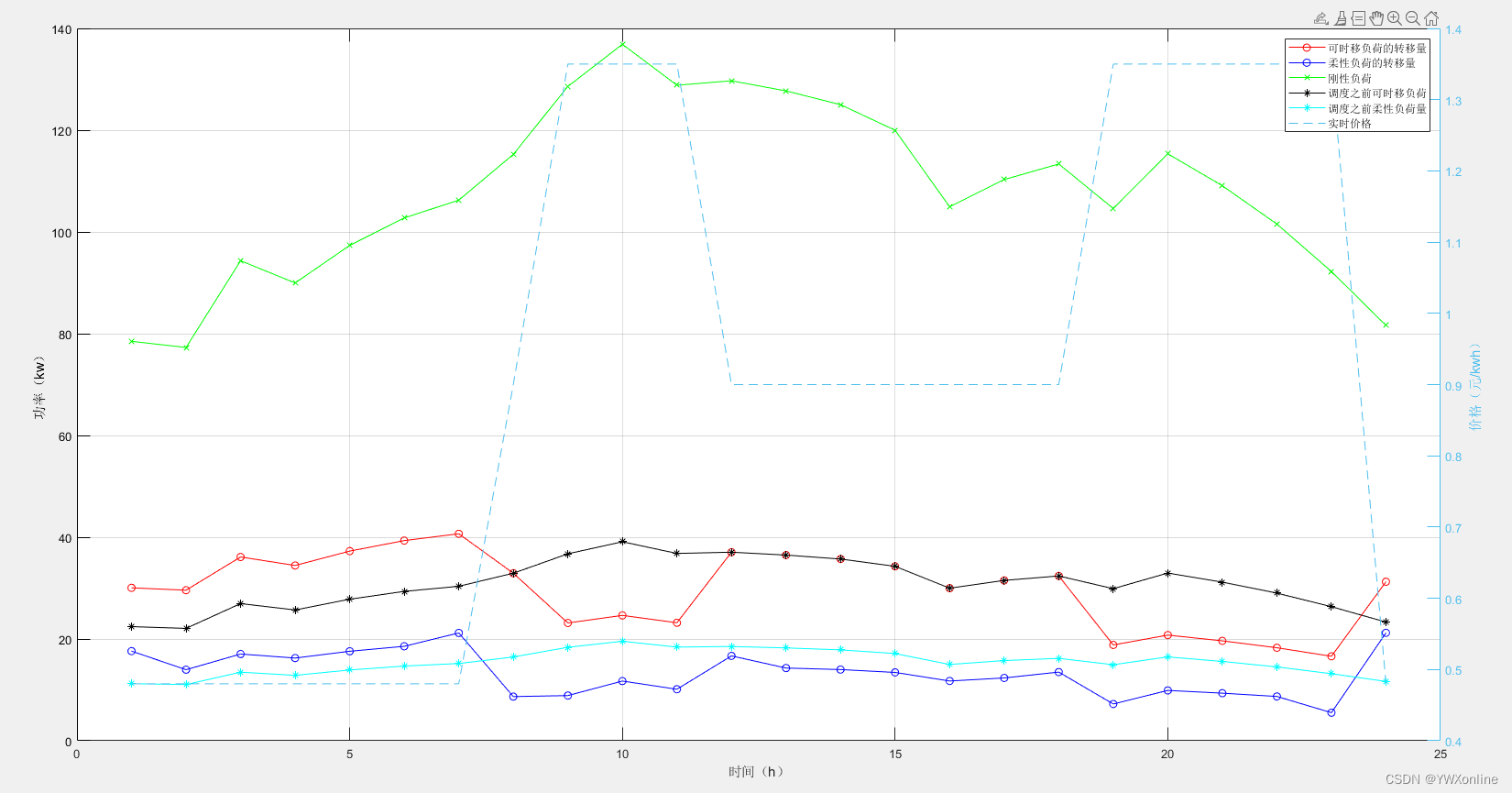
针对微电网中可时移,柔性,基础负荷的电价响应模型---代码解析
前言: 在上两篇帖子中,讲解了我对于粒子群算法的理解,站在巨人的肩膀上去回望:科研前辈们确实非常牛逼,所以它才成为了非常经典的算法。这篇帖子主要是想分享一下,对于微电网、电力系统的论文中,…...

git使用http协议时免密pull和push方法
1、创建文件 在项目目录下创建.git-credentials文件,内容如下,填入自己的用户名和密码即可,如果是gitlab,把地址换成自己的gitlab的地址即可。 https://{用户名}:{密码}github.com2、终端执行 git config --global credential.…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
