05-5.5.1 哈夫曼树
👋 Hi, I’m @Beast Cheng
👀 I’m interested in photography, hiking, landscape…
🌱 I’m currently learning python, javascript, kotlin…
📫 How to reach me --> 458290771@qq.com
喜欢《数据结构》部分笔记的小伙伴可以订阅专栏,今后还会不断更新。🧑💻
感兴趣的小伙伴可以点一下订阅、收藏、关注!🚀
谢谢大家!🙏
带权路径长度
结点的 权 :有某种现实含义的数值(如:表示结点的重要性等)
结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积
树的带权路径长度:树中所有 叶结点 的带权路径长度之和(WPL:Weighted Path Length)
定义
在含有 n 个带权叶结点的二叉树中,其中 带权路径长度(WPL)最小的二叉树 称为 哈夫曼树 ,也称 最优二叉树
哈夫曼树的构造
给定 n 个权值分别为 w 1 , w 2 , . . . , w n w_1,w_2,...,w_n w1,w2,...,wn 的结点,构造哈夫曼树的算法描述如下:
- 将这 n 个结点分别作为 n 棵仅含一个结点的二叉树,构成森林 F
- 构造一个新结点,从F中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值置为左、右子树上根结点的权值之和
- 从 F 中删除刚才选出的两棵树,同时将新得到的树加入 F 中
- 重复步骤 2 和 步骤 3 ,直至 F 中只剩下一棵树为止
结论:
- 每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大
- 哈夫曼树的结点总数为 2 n − 1 2n-1 2n−1
- 哈夫曼树中不存在度为 1 的结点
哈夫曼编码
固定长度编码:每个字符用相等长度的二进制位表示
可变长度编码:允许对不同字符用不等长的二进制位表示
若没有一个编码是令一个编码的前缀,则称这样的编码是 前缀编码
由哈夫曼树得到 哈夫曼编码 ——字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点的权值,根据之前介绍的方法构造哈夫曼树
相关文章:

05-5.5.1 哈夫曼树
👋 Hi, I’m Beast Cheng 👀 I’m interested in photography, hiking, landscape… 🌱 I’m currently learning python, javascript, kotlin… 📫 How to reach me --> 458290771qq.com 喜欢《数据结构》部分笔记的小伙伴可以…...

夯实网络底座:智能云解析助推新基建发展再上新台阶
在数字化浪潮汹涌澎湃的今天,互联网已成为社会运转不可或缺的基础设施。而在这背后,DNS(域名系统)作为互联网的底座,其重要性不言而喻。随着云计算、大数据、人工智能、IPv6等新基建的迅猛发展,传统的DNS服…...

时间戳转时间格式小记——个位数月份 如何去掉补位0的情况
工作中遇到的问题小记一下 时间戳:1710172800 时间格式:2024-03-12 00:00:00 在无要求的情况下这种情况很OK 当我们需要时间格式为:2024-3-12 00:00:00 那常规情况就不适用 解决: import time sjc 1710172800 # Windows 环境…...
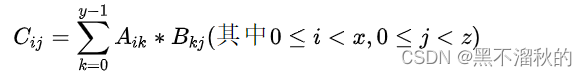
C++ 矩阵乘法
描述 如果A是个x行y列的矩阵,B是个y行z列的矩阵,把A和B相乘,其结果将是另一个x行z列的矩阵C。这个矩阵的每个元素是由下面的公式决定的 矩阵的大小不超过100*100 输入描述: 第一行包含一个正整数x,代表第一个矩阵的…...

热门开源项目推荐
文章目录 1. OpenAIs GPT-42. TensorFlow 3.03. Kubernetes 1.304. React 195. PyTorch 2.06. Deno 2.07. Home Assistant总结 开源社区的不断壮大,越来越多的开发者和企业开始重视和参与开源项目。开源不仅促进了技术的快速迭代和创新,还为广大开发者提…...
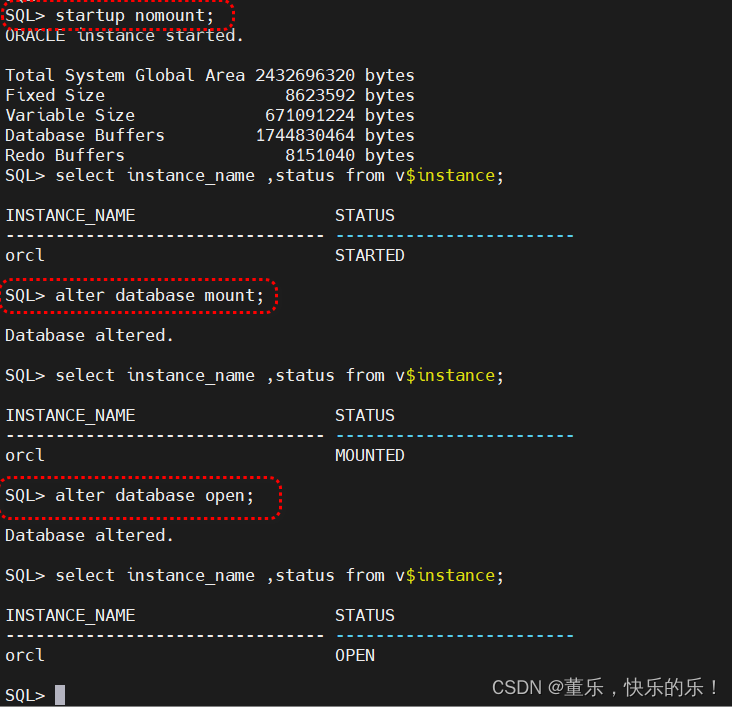
Study--Oracle-03-数据库常规操作
一路走来,所有遇到的人,帮助过我的、伤害过我的都是朋友,没有一个是敌人。 一、oracle 版本及主要功能 二、数据安装完成后常用操作SQL 1、检查数据库监听状态 监听的常用命令 启动:[oracleoracle u01]$ lsnrctl stop 停止&am…...

OpenCloudOS 8.8 一键安装 Oracle 19C 单机
前言 Oracle 一键安装脚本,演示 OpenCloudOS 8.8 一键安装 Oracle 19C 单机(231017)过程(全程无需人工干预)。 ⭐️ 脚本下载地址:Shell脚本安装Oracle数据库 安装准备 1、安装好操作系统,建议…...

【Android】【Java】【每日练手3】Android的四个主要组件使用示例
Android的四个主要组件是活动(Activity)、服务(Service)、广播接收器(Broadcast Receiver)和内容提供器(Content Provider)。下面通过一个简单的示例来介绍这四个组件及其用法。 示…...

代码随想三刷二叉树篇2
代码随想三刷二叉树篇2 101. 对称二叉树题目代码 104. 二叉树的最大深度题目代码 111. 二叉树的最小深度题目代码 222. 完全二叉树的节点个数题目代码 110. 平衡二叉树题目代码 257. 二叉树的所有路径题目代码 101. 对称二叉树 题目 链接 代码 /*** Definition for a binar…...

QT pro包含库文件目录符号含义
直接调用DLL需要三个文件,头文件(.h)、导入库文件(.lib)、动态链接库(.dll), 注意:在qtCreaor中生成的动态库库文件文件为.a结尾,vs生成的动态链接库是.lib结尾 1、首先我们把 .h与.lib/.a 文件复制到程序当前目录下,…...

uniapp怎么进行页面的跳转
在 UniApp 中,页面的跳转主要通过 navigator 组件或者 API 调用实现。以下是几种常见的页面跳转方法: 使用 <navigator> 组件 <navigator> 组件是页面链接的组件,类似于 HTML 中的 <a> 标签。你可以通过 url 属性指定要跳…...

数据库管理-第205期 换个角度看23ai(20240617)
数据库管理205期 2024-06-17 数据库管理-第205期 换个角度看23ai(20240617)1 规范应用开发2 融合总结 数据库管理-第205期 换个角度看23ai(20240617) 作者:胖头鱼的鱼缸(尹海文) Oracle ACE Pro…...

深入解析PHP函数
PHP函数是一种重要的编程概念,它可以帮助开发者组织和管理代码,提高代码的可重用性和可维护性。在PHP中,函数可以完成各种任务,从简单的数学计算到复杂的数据库查询和数据处理。本文将从多个角度探讨PHP函数的应用,涵盖…...

elasticsearch结构化搜索
Elasticsearch的结构化搜索(Structured Search)是指对具有明确格式和结构的数据进行搜索的过程。这类数据包括日期、时间、数字、布尔值等,它们都有精确的格式,可以进行逻辑操作,比如比较数值范围或判断值的大小。结构…...

街道网格宣传稿件投稿我知道了好方法
作为街道信息宣传员,我的日常是将街道的每一项重要活动、每一份温暖故事编织成文字,传递给公众。这份工作既充满挑战又极具意义,但在最初,我却在这份看似简单的任务上屡屡受阻。那时,我的投稿方式单一且传统——依赖电子邮件,将稿件发送至各大媒体的投稿箱。我本以为,只要内容足…...

电脑有线无线一起用怎么设置
要在电脑上同时使用有线和无线网络,可以通过以下几种方法进行设置: 调整网络高级设置: 进入“网络和共享中心”。点击“更改适配器设置”。按键盘Alt键调出菜单栏,然后点击“高级→高级设置”。在“适配器和绑定”标签页下可以对可…...
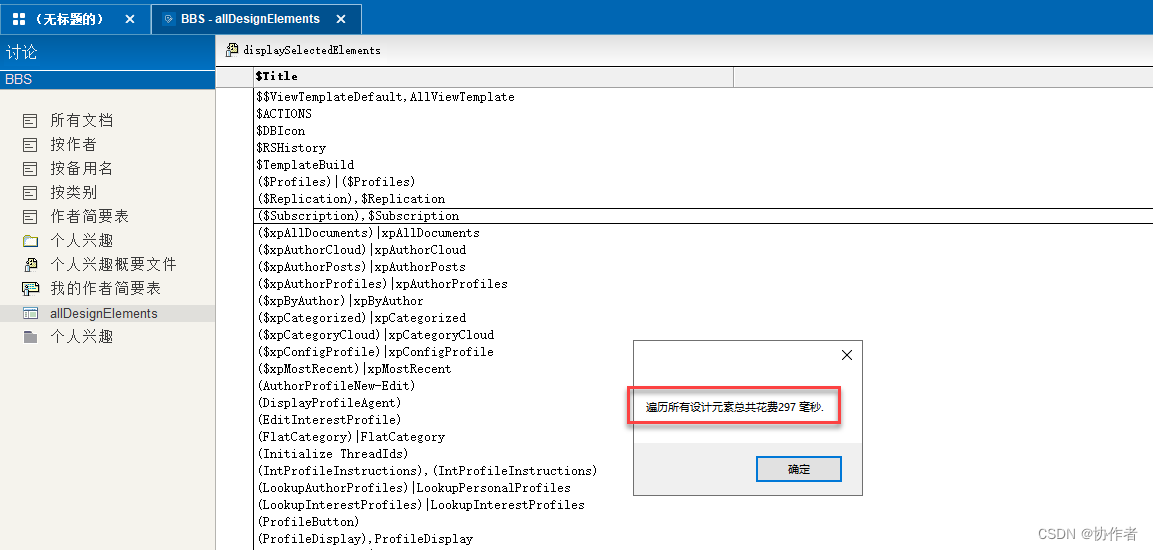
通过LotusScript中的NotesDateTime类来进行时间计算
大家好,才是真的好。 今天我们介绍的是时间日期处理,其实以前也讲过,主要是通过LotusScript中的NotesDateTime类来进行时间计算。 但是这里也存在一个问题:就是时间日期类的比较只能计算出秒,不能计算出毫秒。 毕竟…...

【前端面经】数组算法题解
目录 题目一:两数之和题目二:最长无重复字符子串题目三:合并两个有序数组题目四:寻找数组中的峰值 题目一:两数之和 描述:给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目…...
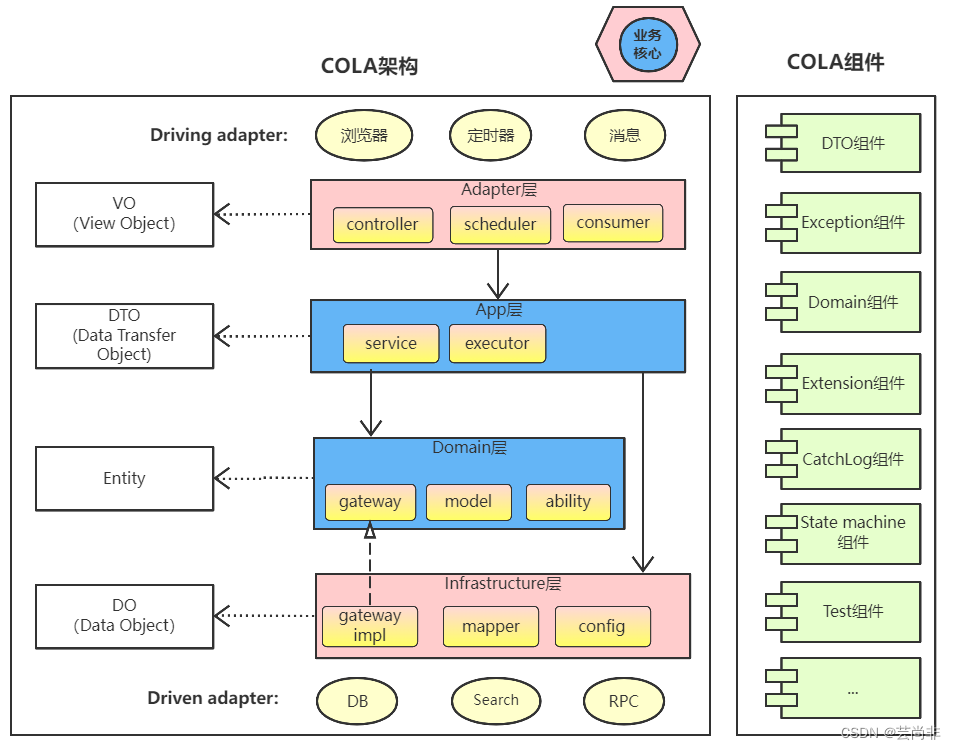
java架构设计-COLA
参考:https://github.com/alibaba/COLA 架构 要素:组成架构的重要元素 结构:要素直接的关系 意义:定义良好的结构,治理应用复杂度,降低系统熵值,改善混乱状态 创建COLA应用: mvn …...
【进阶篇-Day3:JAVA接口新特性、代码块、内部类、Lambda表达式、组件等的介绍】
目录 1、接口新特性1.1 JDK8的新特性1.2 JDK9的新特性 2、代码块2.1 代码块的定义2.2 代码块的分类 3、内部类3.1 内部类的定义3.2 内部类成员访问3.3 学习内部类的原因3.4 内部类的分类3.4.1 成员内部类3.4.2 静态内部类3.4.3 局部内部类3.4.4 匿名内部类(1&#x…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
