深度学习入门5——为什么神经网络可以学习?
在理解神经网络的可学习性之前,需要先从数学中的导数、数值微分、偏导数、梯度等概念入手,从而理解为什么神经网络具备学习能力。
1.数值微分的定义
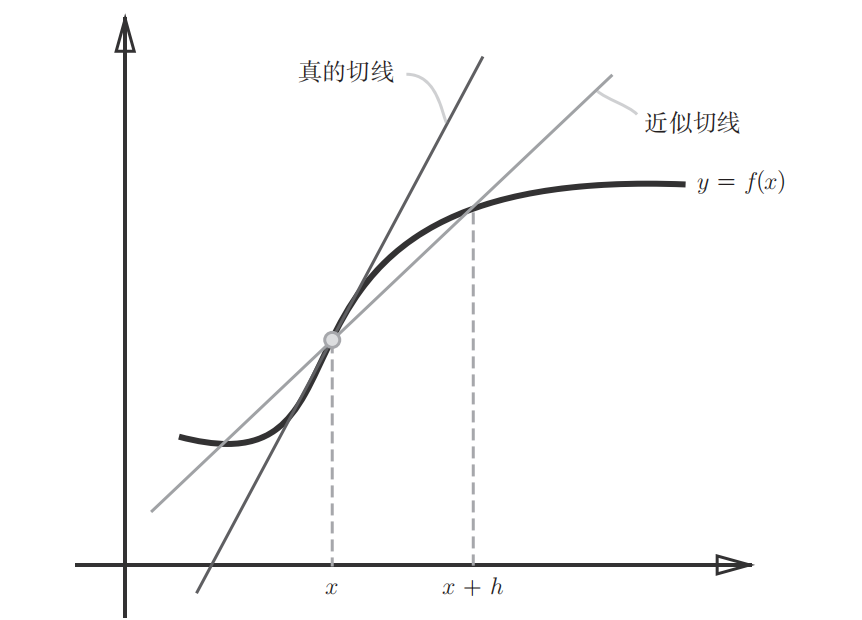
先从导数出发理解什么是梯度。某一点的导数直观理解就是在该点的切线的斜率。在数学中导数表示某个瞬时的变化量,如下公式表示:

上述利用微小的差分求导数的过程称为数值微分(numerical differentiation),公式(1)表示的是前向差分(f(x+h)-f(x)),因为h无法无限趋近于0,所以存在误差(如下图所示)。为了减小这种数值微分误差,可以用中心差分(f(x+h)-f(x-h))减小误差。
2.数值微分的例子
以下面这个二次函数为例,对其数在x = 5和x = 10处进行求导。

import numpy as np
import matplotlib.pylab as pltdef numerical_diff(f, x):h = 1e-4 # 0.0001return (f(x+h) - f(x-h)) / (2*h) # 中心差分def function_1(x):return 0.01*x**2 + 0.1*x def tangent_line(f, x):d = numerical_diff(f, x)print(d) # 0.1999999999990898 0.2999999999986347y = f(x) - d*xreturn lambda t: d*t + y#该函数首先调用numerical_diff函数来计算函数f在点x处的导数d,然后根据切线的方程 y = ax + b 中的斜率和截距来计算切线的斜率d和截距y。最后返回一个匿名函数,该函数接受一个参数 t,并返回切线上在 t 处的函数值。
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")tf1 = tangent_line(function_1, 5) # x=5处的切线方程
tf2 = tangent_line(function_1, 10) # x=10处的切方程
y1 = tf1(x)
y2 = tf2(x)plt.plot(x, y)
plt.plot(x, y1)
plt.plot(x, y2)
plt.show()
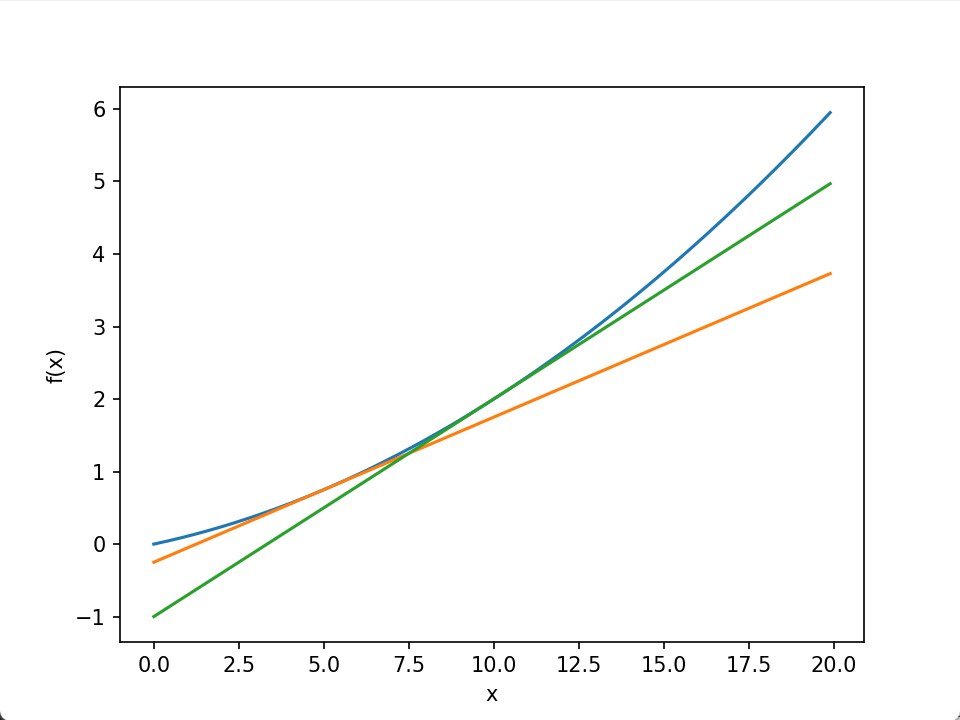
3.偏导数和梯度
下式表示的是包含两个变量的函数,可以看为计算平面内点的坐标的平方和函数:

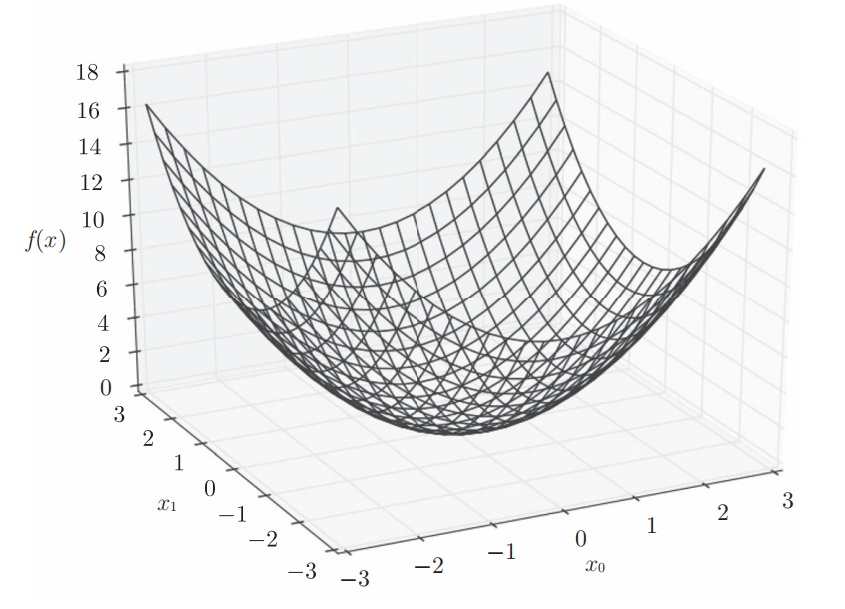
求某个变量的偏导数时,需要将多个变量中的某一个变量定为目标变量,并将其他变量固定为某个值才能求解。下面是该函数(由全部变量的偏导数汇总而成的向量)梯度(gradient)的可视化。
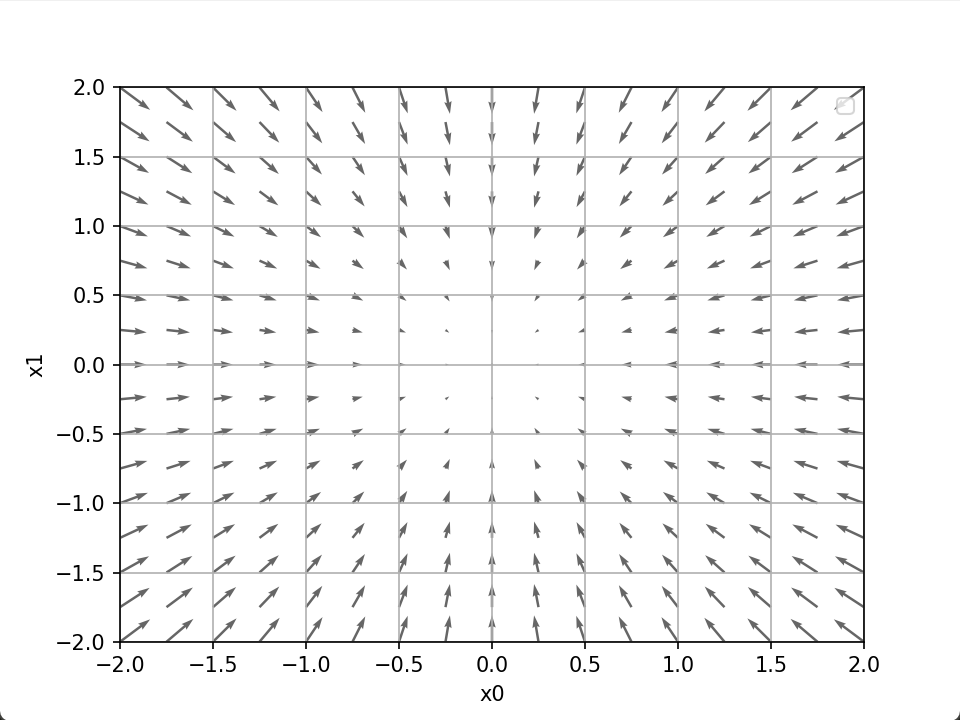
4.梯度法
机器学习的主要任务是在学习时寻找最优参数,而神经网络也必须在学习时找到最优的参数(权重和偏置)。上面介绍的函数其梯度指向的是函数最小值的方向,但是在复杂函数也就是一般的情况下,梯度下降的方向不一定是指向函数最小值,因为还可能存在鞍点(极小值、局部极值)。一般来说,损失函数很复杂,参数空间庞大,不知道它在何处能取得最小值,因此可以利用梯度求最小值。梯度法中,函数的取值从当前位置沿着梯度方向前进一定距离,然后在新的地方重新求梯度,再沿着新梯度方向前进,如此反复,不断地沿梯度方向前进。通过不断地沿梯度方向前进,逐渐减小函数值的过程就是梯度法。其中寻找最小值的梯度法称为梯度下降法,寻找最大值的梯度法称为梯度上升法。一般情况下,在神经网络中主要指的是梯度下降法,要最小化损失函数,最终得到最小值处对应的神经网络的权重和偏置,此时神经网络就被训练好了。
def gradient_descent(f, init_x, lr=0.01, step_num=100):x = init_xfor i in range(step_num):grad = numerical_gradient(f, x)x -= lr * gradreturn xdef function_2(x):return x[0]**2 + x[1]**2init_x = np.array([-3.0, 4.0])
gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100) # 得到损失函数最小值对应的坐标点(0, 0),array([ -6.11110793e-10, 8.14814391e-10])
f是要进行最优化的函数,,init_x是初始值,lr是学习率learning rate,step_num是梯度法的重复次数。在上面的例子中,学习率设置为0.1。学习率设置的过大或过小对于损失函数的收敛都不利,因此选取合适的学习率也是神经网络超参数的一个重要部分。与神经网络的权重和偏置不同,学习率需要人为设定。如何理解学习率过大过小对损失函数收敛的影响呢?现在我们将损失函数想象成一口大铁锅,锅底的位置就是损失函数达到最小值的地方。当学习率设置的过小时,此时可以看成是放了一只小蚂蚁在锅的外边缘,步子很小,它需要走很多步才能走到底部,耗时长且效率慢,而且有可能陷入“局部最优”。而学习率过大则可以想象成是跳蚤,它每次向前运动的幅度很大,仅略小于锅的尺寸,它会在锅的侧壁来回弹跳,而到达不了锅底。
5.神经网络的梯度
神经网络在学习的过程中也要进行梯度的计算。以一个只有一个形状为2 × 3的权重W的神经网络为例,它的损失函数用L表示,那么梯度

可表示为如下:

求梯度代码实现:
import sys, os
import numpy as npdef softmax(x):if x.ndim == 2:x = x.Tx = x - np.max(x, axis=0)y = np.exp(x) / np.sum(np.exp(x), axis=0)return y.T x = x - np.max(x) # 溢出对策return np.exp(x) / np.sum(np.exp(x))def cross_entropy_error(y, t):if y.ndim == 1:t = t.reshape(1, t.size)y = y.reshape(1, y.size)# 监督数据是one-hot-vector的情况下,转换为正确解标签的索引if t.size == y.size:t = t.argmax(axis=1)batch_size = y.shape[0]return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_sizedef numerical_gradient(f, x):h = 1e-4 # 0.0001grad = np.zeros_like(x)it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])while not it.finished:idx = it.multi_indextmp_val = x[idx]x[idx] = float(tmp_val) + hfxh1 = f(x) # f(x+h)x[idx] = tmp_val - h fxh2 = f(x) # f(x-h)grad[idx] = (fxh1 - fxh2) / (2*h)x[idx] = tmp_val # 还原值it.iternext() return gradclass simpleNet:def __init__(self):self.W = np.random.randn(2,3)def predict(self, x):return np.dot(x, self.W)def loss(self, x, t):z = self.predict(x)y = softmax(z)loss = cross_entropy_error(y, t)return lossx = np.array([0.6, 0.9])
t = np.array([0, 0, 1])net = simpleNet()f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)print(dW)
结果:

6.神经网络学习的实现流程
完整实现参见《深度学习入门:基于python的理论与实现》第四章第五节的内容。以上是神经网路学习的所有基本概念,包括“mini-batch”、“梯度”、“梯度下降法”等概念。神经网络的学习过程为:
前提:训练数据是均匀的,即是被shuffle(打乱)过的。其次神经网络已经存在较为合适的权重和偏置。
step1:按照mini-batch的方法从训练数据中随机选出一部分数据进行训练。
step2:计算各个权重参数的梯度,梯度表示函数值减小最多的方向。
step3:将权重参数沿梯度方向进行微小更新(lr,学习率)。
step4:重复 step1、step2、step3。
上面使用的数据时从原始数据中随机选择的mini-batch数据,所以又称之为随机梯度下降法(stochastic gradient descent),即对随机选择的数据进行的梯度下降法。在很多深度学习框架中,其一般由一个名为SGD的函数进行实现。为了保证所有的训练数据都被使用,一般做法是事先将所有训练数据随机打乱,然后按指定的批次大小按序生成mini-batch。这样每个mini-batch均有一个索引号,然后用索引号可以遍历所有的mini-batch。遍历一次所有数据,就称为一个epoch。
相关文章:

深度学习入门5——为什么神经网络可以学习?
在理解神经网络的可学习性之前,需要先从数学中的导数、数值微分、偏导数、梯度等概念入手,从而理解为什么神经网络具备学习能力。 1.数值微分的定义 先从导数出发理解什么是梯度。某一点的导数直观理解就是在该点的切线的斜率。在数学中导数表示某个瞬…...

Integer溢出问题
0. 背景 在刷 LeetCode 时,代码的执行结果与预期出现了偏差,原因是 Int 值超过了允许范围 [ − 2 31 , 2 31 − 1 ] [-2^{31},2^{31}-1 ] [−231,231−1]。工作中从来没有遇到过这种情况,之前的认知是如果 Int 中存储的值超过了允许范围也许…...

软件测试全面指南:提升软件质量的系统流程
一、引言 随着软件行业的飞速发展,确保软件质量、稳定性和用户体验已成为企业竞争的关键。本文档旨在为测试团队提供一套全面的软件测试指南,通过规范测试用例管理、功能测试、接口测试、性能测试及缺陷管理等流程,助力测试团队实现高效、系统…...

《逆贫大叔》:一部穿越时光的温情史诗
《逆贫大叔》:一部穿越时光的温情史诗 在历史的长河中,有些故事能够穿越时光的尘埃,直击人心。《逆贫大叔》就是这样一部作品,它不仅是一部电视剧,更是一段历史的缩影,一次心灵的触动。 背景设定࿱…...

【电机控制】FOC算法验证步骤——PWM、ADC
【电机控制】FOC算法验证步骤 文章目录 前言一、PWM——不接电机1、PWMA-H-50%2、PWMB-H-25%3、PWMC-H-0%4、PWMA-L-50%5、PWMB-L-75%6、PWMC-L-100% 二、ADC——不接电机1.电流零点稳定性、ADC读取的OFFSET2.电流钳准备3.运放电路分析1.电路OFFSET2.AOP3.采样电路的采样值范围…...

如何衡量llm 数据集的多样性
衡量大型语言模型(LLM)数据集的多样性是一个复杂的问题,因为多样性可以从多个角度来考虑。以下是一些常用的方法和指标来评估数据集的多样性: 词汇多样性: 类型-词符比(Type-Token Ratio, TTR)…...

编程天才是什么意思
编程天才是什么意思 编程天才,这个词汇似乎充满了神秘与敬畏的色彩。那么,它究竟意味着什么呢?在本文中,我们将从四个方面、五个方面、六个方面和七个方面深入探讨编程天才的内涵与外延,带您领略这一领域的独特魅力。…...
创建npm私包
参考文章: 使用双重身份验证访问 npm | npm 中文网 私有npm包的实例详解-js教程-PHP中文网 1.注册npm账号 npm官网: npm | Home 2.安装node 百度挺多的,安装完后,检查是否安装成功就行 3.写一个简单的模块 创建个文件夹&am…...

provider追加android:name的命名有哪些?
在Android中,为<provider>元素添加android:name属性时,命名应遵循Android组件的命名规范和包名的命名规范。以下是一些关于命名android:name的要点: 包名前缀:android:name属性的值通常应以包名开始,这是应用程序…...
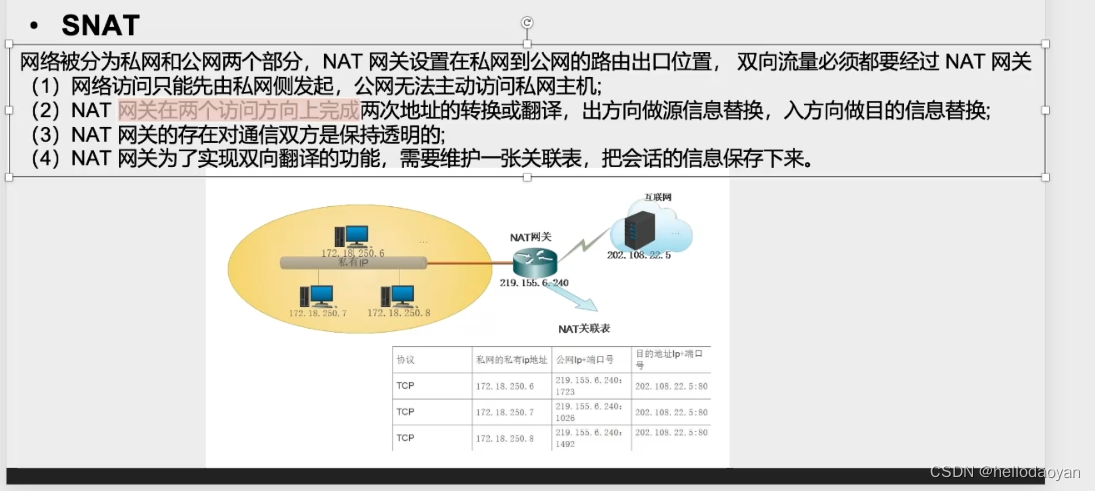
长亭网络通信基础
长亭笔试之前就已经学过一遍了 这算温故而知新吧 TCP/IP 首先我在这里默写一下之前的7层和4层 应用层 应 【表示层 数据格式转换 传 【会话层 …...

hdfs源码解析之DFSClient
1、DFSClient类简介 DFSClient 是 Hadoop 分布式文件系统(HDFS)中的一个核心类,用于客户端与 HDFS 之间的交互。它提供了一组方法,使客户端应用程序可以方便地与 HDFS 进行通信,包括文件的读取、写入、创建、删除、重命…...

智能化立体仓库的种类有哪些?
在仓储运输系统中,自动化立体仓库可充分利用空间储存货物,故而也被称之为高层货架仓库。在实际应用中,自动化仓库系统是不需人工处理的情况下能自动存储和取出物料的系统。那么,智能化立体仓库的种类有哪些?下面就让小…...

Stable Diffusion 3 如何下载安装使用及性能优化
Stable Diffusion 3 Stable Diffusion 3(SD3),Stability AI最新推出的Stable Diffusion模型系列,现在可以在Hugging Face Hub上使用,并且可以与Diffusers一起使用。 今天发布的模型是Stable Diffusion 3 Medium&…...

c语言操作符详解
操作符详解 正数的原码反码补码相同 负数的原码最高位数是1,正数为0 整数在内存中存储的是补码 负数的左移与右移,移的是补码,打印的是源码 补码-1取反就是原码。 左移有乘2的效果 左移和右移只针对整数。 vs里的右移操作赋采用的是算数右…...
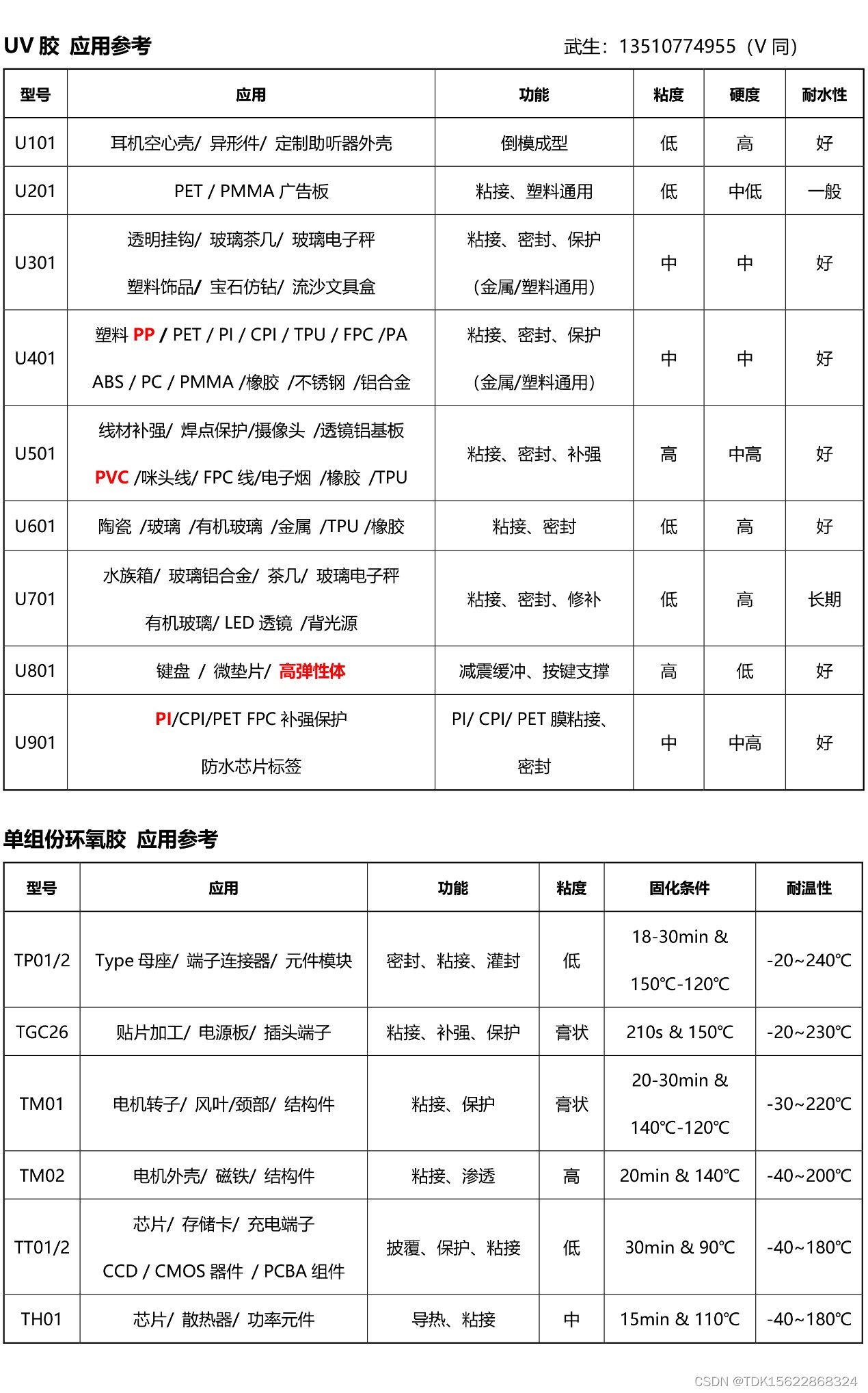
【耐水好】强耐水UV胶水它的粘接强度和普通UV胶水比如何呢
【耐水好】强耐水UV胶水它的粘接强度和普通UV胶水比如何呢 强耐水UV胶水的粘接强度与普通UV胶水相比,具有显著的优势。以下是详细的比较和归纳: 固化方式: 两者都是通过紫外线(UV)照射进行固化,但强耐水UV…...
jumpserver堡垒机集群搭建
1、环境 操作系统:龙蜥os 7.9 firewall-cmd --permanent --zonepublic --remove-servicessh firewall-cmd --permanent --zonepublic --add-rich-rulerule familyipv4 source address10.90.101.1 port port22 protocoltcp accept firewall-cmd --reload2、安装NFS…...

Termius for Mac/Win:跨平台多协议远程管理利器
Termius for Mac/Win是一款备受瞩目的跨平台多协议远程管理软件,以其卓越的性能、丰富的功能和便捷的操作体验,赢得了广大用户的青睐。无论是在企业IT管理、系统维护,还是个人远程连接、文件传输等方面,Termius都展现出了出色的实…...

Unity OpenCVForUnity 安装和第二个案例详解 <二>
目录 一、前言 二、场景介绍 1.WebCamTextureToMatExample脚本 2.FpsMonitor脚本 三、 结构体Scaler 四、找到相机并使用 1.相机的启用 2.格式转换 a.把webCamTexture转换成Mat b.把Mat转换成Texture2D 五、脚本组合 六、作者的碎碎念 一、前言 第二个案例…...

Lua实现自定义函数面向对象编程
本文目录 1、引言2、原理3、实例4、层析验证 文章对应视频教程: 暂无,可以关注我的B站账号等待更新。 点击图片或链接访问我的B站主页~~~ 1、引言 在现代软件开发中,面向对象编程(OOP)已经成为一种广泛使用的编程范式…...
docker安装消息队列mq中的rabbit服务
在现代化的分布式系统中,消息队列(Message Queue, MQ)已经成为了一种不可或缺的组件。RabbitMQ作为一款高性能、开源的消息队列软件,因其高可用性、可扩展性和易用性而广受欢迎。本文将详细介绍如何在Docker环境中安装RabbitMQ服务…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
