当前位置：首页 > news >正文

逻辑蕴含、函数依赖集的闭包、Armstrong公理、属性集闭包

news 2026/2/11 2:42:11

一、引言

Armstrong公理-从给定的函数依赖集得到关系模式的完整依赖集

二、逻辑蕴含

1、定义

设F是关系模式R上的函数依赖集，X、Y是R的属性子集，对于R的每个满足F的关系实例r，若函数

依赖 $X\rightarrow Y$ 都成立，则称F逻辑蕴含 $X\rightarrow Y$ 。

记为： $F\vdash X\rightarrow Y$

F逻辑蕴含的所有函数依赖的集合，称为函数依赖集F的闭包，并记为 $F^{+}$ 。

记为： $F^{+}=$ { $X\rightarrow Y\mid F\vdash X\rightarrow Y$ }

三、Armstrong公理

1、定义

1974年Armstrong提出一套推理规则，被称为Armstrong公理

2、作用

利用推理规则从给定的函数依赖中推导出其蕴含的函数依赖

3、内容

包含三条基本规则和三条扩充规则

4、实例

关系模式R（U，F）:

（1）U为R的属性集

（2）F是U上的函数依赖集

（3）X、Y、Z、W是U的子集

（4）子集X、Y的并集记为XY

四、Armstrong公理的内容

1、三条基本推理规则

（1）自反律

若 $Y\subseteq X$ ，则 $X\rightarrow Y$

（2）增广律

若 $X\rightarrow Y$ 为F所蕴含，则 $XZ\rightarrow YZ$

（3）传递律

若 $X\rightarrow Y$ 、 $Y\rightarrow Z$ 为F所蕴含，则 $X\rightarrow Z$

2、三条扩充推理规则

（1）合并规则

若 $X\rightarrow Y$ 、 $X\rightarrow Z$ ，则 $X\rightarrow YZ$ （增广律，传递律）

（2）伪传递规则

若 $X\rightarrow Y$ 、 $WY\rightarrow Z$ ，则 $XW\rightarrow Z$ （增广律、传递律）

（3）分解规则

若 $X\rightarrow Y$ 、 $Z\subseteq Y$ ，则 $X\rightarrow Z$ （自反律、传递律）

3、合并规则和分解规则可得一个重要的事实

引理1：

$X\rightarrow A_{1}A_{2}...A_{k}$ 成立的充分必要条件是 $X\rightarrow A_{i}$ 成立（i=1,2，...，k）

五、属性集闭包

1、引言

对于一个函数依赖集，其闭包中所包含的函数依赖有很多，从函数依赖集F求其闭包是很困难的，

对于任意的函数依赖，通过判断是否在闭包中来判断该函数依赖是否为函数依赖集F所逻辑蕴含是

很困难的，于是引入了属性集闭包的概念

2、属性集闭包的定义

在R(U,F)中，F是属性集U上的一组函数依赖， $X\subseteq U$ ，则属性集X关于函数依赖集F的闭包 $X{_{F}}^{+}$

定义为：

$X{_{F}}^{+}$ 是 $F^{+}$ 中所有函数依赖于属性集X的所有属性的集合

3、引理2：

由引理2，就可以将 $X\rightarrow Y$ 是否属于F的闭包的问题转化为判断Y是否为X关于F的闭包的子集的问题，而X关于F的闭包可由算法帮助实现

六、使用算法求解属性集闭包

1、明确概念

（1）函数依赖集F的闭包是F所蕴含的函数依赖的集合

（2）属性集X关于函数依赖集F的闭包是F的闭包中的函数依赖的决定因素是属性集X的属性的集合，以下简称为属性集闭包

2、求 $X{_{F}}^{+}$ （X的属性集闭包）的一个算法

输入：属性集X和和函数依赖集F

输出：属性集X关于函数依赖集F的闭包 $X{_{F}}^{+}$

算法实现流程：

（1）开始

（2）给 $X{_{F}}^{+}$ 赋初值X

（3）判断 $X{_{F}}^{+}$ 的值与上一次相比是否改变，如果改变，执行（4），没改变，执行（5）

（4）对F中的每一个函数依赖 $Y\rightarrow Z$ ，如果 $Y\subseteq X_{F}^{+}$ ，则将Z并入到 $X{_{F}}^{+}$ 中，执行（3）

（5）输出 $X{_{F}}^{+}$ ，结束

3、举例：使用算法计算属性集X的闭包 $X{_{F}}^{+}$

七、举例：通过属性集闭包来判断函数依赖是否在函数依赖集F的闭包中

八、小结

1、Armstrong公理的有效性

从F中已有的函数依赖利用Armstrong公理导出的每一个函数依赖 $Y\rightarrow Z\in F^{+}$

2、Armstrong公理的完备性

函数依赖集F所蕴含的函数依赖，即 $F^{+}$ 中的每一个函数依赖都可以利用Armstrong公理推导出来

逻辑蕴含、函数依赖集的闭包、Armstrong公理、属性集闭包

一、引言 Armstrong公理-从给定的函数依赖集得到关系模式的完整依赖集二、逻辑蕴含 1、定义设F是关系模式R上的函数依赖集，X、Y是R的属性子集，对于R的每个满足F的关系实例r，若函数依赖都成立，则称F逻辑蕴含。记为&#…...

编程日记 2024/6/19 19:48:44

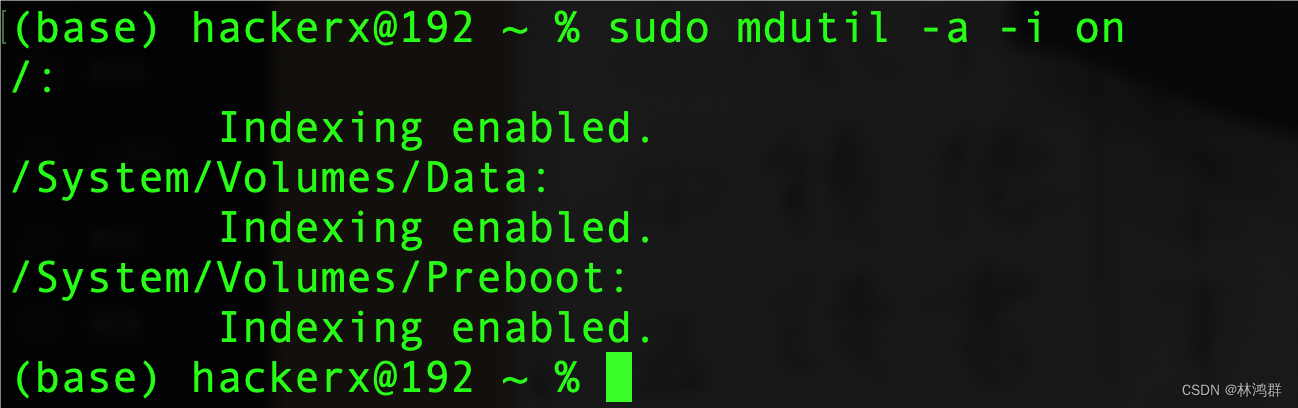
macOS聚集搜索功能开启与关闭

按下command空格弹出使用搜索关闭搜索 sudo mdutil -a -i off 启用搜索 sudo mdutil -a -i on...

编程日记 2024/6/19 19:46:40

大模型“诸神之战”，落地才是赛点

ChatGPT 诞生已经快一年，你还在与它对话吗？ 有的人用来写报告、改代码，让它成为得力帮手；有的人却只是“调戏”个两三回，让它创作诗歌或故事，便不再“宠幸”。根据网站分析工具 SimilarWeb 的数据&#…...

编程日记 2024/6/19 19:45:36

接口重放攻击

如何保证接口安全，做到防篡改防重放？_接口防止串改-CSDN博客接口安全设计之防篡改和防重放_接口防篡改机制-CSDN博客基于nonce timestamp 的方案 nonce的意思是仅一次有效的随机字符串，要求每次请求时该参数要保证不同。实际使用用户信息…...

编程日记 2024/6/19 19:44:33

MySQL学习笔记-进阶篇-SQL优化

SQL优化插入数据 insert优化 1）批量插入 insert into tb_user values(1,Tom),(2,Cat),(3,Jerry); 2）手动提交事务 mysql 默认是自动提交事务，这样会导致频繁的开启和提交事务，影响性能 start transaction insert into tb_us…...

编程日记 2024/6/19 19:43:30

【机器学习】第2章线性回归及最大熵模型

一、概念 1.回归就是用一条曲线对数据点进行拟合，该曲线称为最佳拟合曲线，这个拟合过程称为回归。 2.一个自变量叫一元线性回归，大于一个自变量叫多元线性回归。 （1）多元回归：两个x，一个…...

编程日记 2024/6/19 19:42:26

科技创新对农业发展的影响

科技创新对农业发展的影响深远且广泛，主要体现在以下几个方面： 一、提高农业生产效率引入先进的农业机械设备：新型农业机械设备如无人机、机器人等的应用，显著减轻了农民的劳动强度，提高了农作物的种植效率。利用精…...

编程日记 2024/6/19 19:41:22

Linux 常用命令 - rm 【删除文件或目录】

简介 rm 命令源于英文单词 “remove”，它用于删除文件或目录。rm 是 Linux 系统中最基本的命令之一，用于删除指定的文件或目录。默认情况下，rm 不会删除目录，但可以通过递归删除选项来实现。使用方式 rm [选项]... [文件]...常…...

编程日记 2024/6/19 19:40:19

一血c++

题目描述每一个竞赛选手都无法拒绝拿一血 "一血"其实就是同学们在榜单上看到的深绿色的标记，代表着某道题目，他是第一个通过的。叶苡朋老师是一名资深信奥选手，在大学多次获奖，也是一个资深抢一血爱好者&#xff0…...

编程日记 2024/6/19 19:39:17

无问芯穹Qllm-Eval：制作多模型、多参数、多维度的量化方案

前言近年来，大语言模型（Large Models, LLMs）受到学术界和工业界的广泛关注，得益于其在各种语言生成任务上的出色表现，大语言模型推动了各种人工智能应用（例如ChatGPT、Copilot等）的发展。然而…...

编程日记 2024/6/19 19:38:14

2024-05-31T08:36:09.000+00:00 转换 YYYY-MM-DD HH-MM-SS

function formatDate(date) {// 处理ISO 8601字符串if (typeof date string) {date new Date(date);}// 处理时间戳else if (typeof date number) {date new Date(date * 1000); // 假设后端时间戳为秒，需要乘以1000转换为毫秒}// 自定义格式化，例如…...

编程日记 2024/6/19 19:36:09

reason: the Java file contained parse errors

今天用Maven打包项目时发生一个错误： file: D:\workspace\echoo2.0-xxx-xxx-portal\src\main\java\com\echoo\service\impl\DecDataServiceImpl.java; reason: the Java file contained parse errors 打包报错显示这个类解析错误在IDEA中没有任何错误提示问题所…...

编程日记 2024/6/19 19:35:06

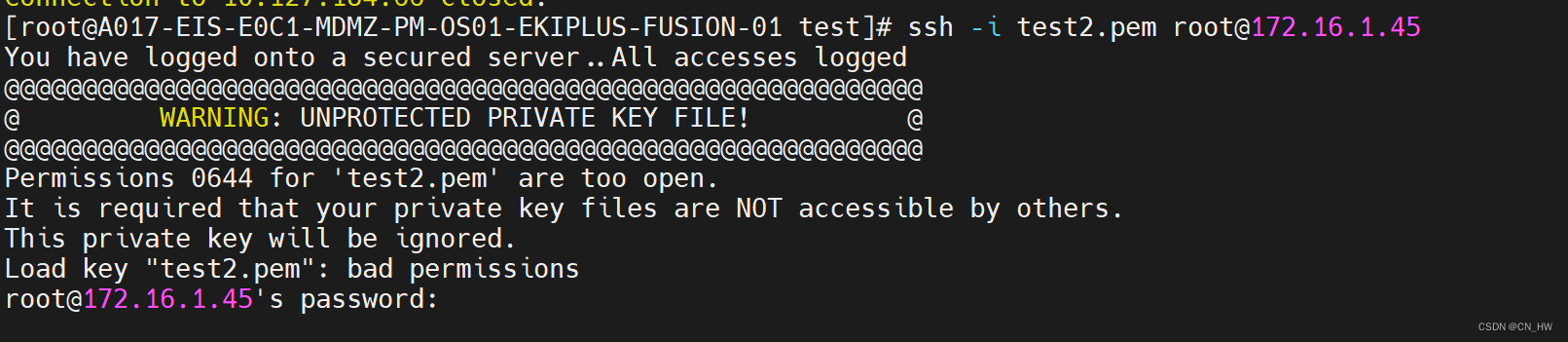
使用密钥对登录服务器

目录 1、使用密钥文件登录服务器 2、登录成功画面： 3、如若出现以下状况，则说明密钥文件登录失败 1、使用密钥文件登录服务器首先需要上传pem文件 2、登录成功画面： 3、如若出现以下状况，则说明密钥文件登录失败解决方法&…...

编程日记 2024/6/19 19:34:03

面试_多线程

线程池线程池的参数有哪些线程池七大参数分别是corePoolSize、maximumPoolSize、keepAliveTime、unit、workQueue、threadFactory、handler corePoolSize：线程池中常驻核心线程数maximumPoolSize：线程池能够容纳同时执行的最大线程数keepAliveTime&…...

编程日记 2024/6/19 19:32:59

跨境电商必备？揭秘原生IP的作用

一、什么是原生IP？ 原生IP（Native IP）是指由互联网服务提供商（ISP）或服务器提供商直接分配给用户的IP地址，这种IP地址直接与用户设备或网络相连，也就是指这个IP的注册地址和服务器机房所在的国…...

编程日记 2024/6/19 19:30:55

mysql竖表变横表不含聚合

文章目录前言一、vertical_table二、转换1.要将其转换为横表形式，例如：2.sql 总结前言在MySQL中将竖表转换为横表（也称为行转列操作），不涉及聚合函数，通常可以通过使用条件判断和自连接来实现。假设有一…...

编程日记 2024/6/19 19:28:52

application/x-www-form-urlencoded和json的区别

application/x-www-form-urlencoded 和 application/json 是两种不同的数据格式，常用于HTTP请求中传递数据。它们各自的特点和使用场景如下： 1. application/x-www-form-urlencoded •特点：这是一种传统的表单提交时采用的编码类型&#x…...

编程日记 2024/6/19 19:26:47

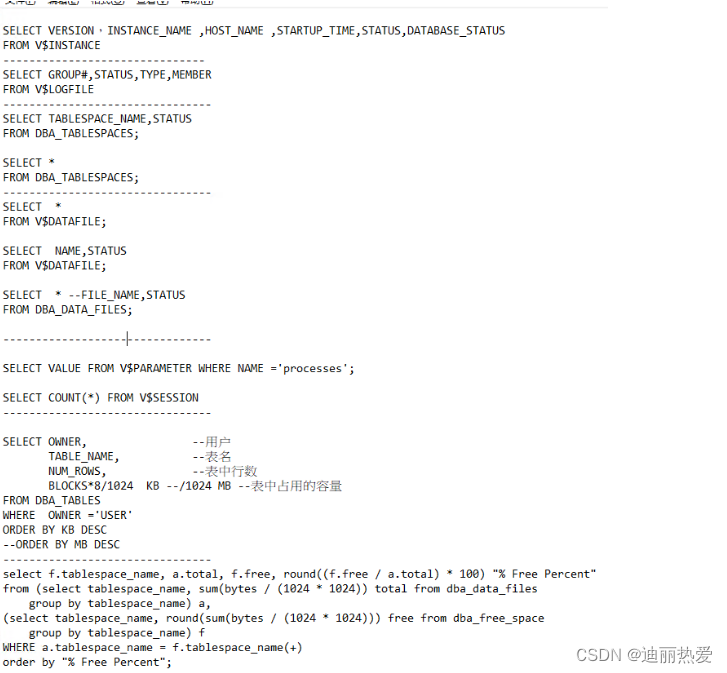
oracle数据库日常保养或巡检语句实践整理汇总

目录 1.目的 2.操作工具 3.实践说明 1.检查Oracle实例状态 2.检查Oracle在线日志状态 3.检查Oracle表空间状态 4.检查Oracle所有数据文件状态 5.检查Oracle数据库连接情况 6.检查Oracle表容量占用大小 7.检查Oracle备份 8.检查数据库表空间的使用情况 4.总结 1.目的 …...

编程日记 2024/6/19 19:25:43

Elasticsearch 第一期：基础的基础概念

前言 Elasticsearch（弹性搜索） ，简称为ES， 它是一个开源的高扩展的分布式全文检索引擎，它提供的功能主要分为：实时存储，实时分析搜索；本身扩展性很好，可以扩展到上百台服…...

编程日记 2024/6/19 19:24:40

MySQL数据库笔记（二）

第一章单行函数 1.1 什么是函数函数的作用是把我们经常使用的代码封装起来，需要的时候直接调用即可。这样既提高了代码效率，又提高了可维护性。在SQL中使用函数，极大地提高了用户对数据库的管理效率。 1.2 定义操作数据对象。接受参数返回一个结果。只对一行进行…...

编程日记 2024/6/19 19:23:36

深入剖析AI大模型：大模型时代的 Prompt 工程全解析

今天聊的内容，我认为是AI开发里面非常重要的内容。它在AI开发里无处不在，当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗"，或者让翻译模型 "将这段合同翻译成商务日语" 时，输入的这句话就是 Prompt。…...

编程新知 2026/2/8 20:42:53

stm32G473的flash模式是单bank还是双bank？

今天突然有人stm32G473的flash模式是单bank还是双bank？由于时间太久，我真忘记了。搜搜发现，还真有人和我一样。见下面的链接：https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

编程新知 2026/2/8 20:41:51

Oracle查询表空间大小

1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

编程新知 2025/11/8 0:24:13

从零开始打造 OpenSTLinux 6.6 Yocto 系统（基于STM32CubeMX）（九）

设备树移植和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下源码修改及编译修改arch/arm/boot/dts/st/Makefile，新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

编程新知 2026/2/5 12:11:18

Python如何给视频添加音频和字幕

在Python中，给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加，包括必要的代码示例和详细解释。环境准备在开始之前，需要安装以下Python库：…...

编程新知 2025/9/3 4:12:17

智能分布式爬虫的数据处理流水线优化：基于深度强化学习的数据质量控制

在数字化浪潮席卷全球的今天，数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具，在大规模数据获取中发挥着关键作用。然而，传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时，常出现数据质…...

编程新知 2026/2/6 1:04:23

视频行为标注工具BehaviLabel（源码+使用介绍+Windows.Exe版本）

前言： 最近在做行为检测相关的模型，用的是时空图卷积网络（STGCN），但原有kinetic-400数据集数据质量较低，需要进行细粒度的标注，同时粗略搜了下已有开源工具基本都集中于图像分割这块&#xff0c…...

编程新知 2026/2/6 5:04:18

安宝特案例丨Vuzix AR智能眼镜集成专业软件，助力卢森堡医院药房转型，赢得辉瑞创新奖

在Vuzix M400 AR智能眼镜的助力下，卢森堡罗伯特舒曼医院（the Robert Schuman Hospitals, HRS）凭借在无菌制剂生产流程中引入增强现实技术（AR）创新项目，荣获了2024年6月7日由卢森堡医院药剂师协会&#xff0…...

编程新知 2026/2/9 2:41:28

CRMEB 中 PHP 短信扩展开发：涵盖一号通、阿里云、腾讯云、创蓝

目前已有一号通短信、阿里云短信、腾讯云短信扩展扩展入口文件文件目录 crmeb\services\sms\Sms.php 默认驱动类型为：一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

编程新知 2025/10/5 5:38:24

NPOI Excel用OLE对象的形式插入文件附件以及插入图片

static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

编程新知 2025/10/6 2:06:51

相关文章：