数据结构之B数
目录
1.概述
2.特点
3.诞生
4.优缺点
4.1.优点
4.2.缺点
5.应用场景
6.C语言中的B树实现例子
7.总结
1.概述
B树(B-tree)是一种自平衡的树数据结构,广泛应用于数据库和文件系统中,以便高效地进行顺序读取、写入以及查找操作。主要思想是保持数据在一种排序状态,且每个节点可以拥有多个子节点,使得系统在磁盘I/O上更加高效。

2.特点
1. 自平衡:自动调整自身结构以保持平衡。
2. 所有叶子节点在同一层:这确保了查找操作的深度相同。
3. 节点的键数量:每个节点包含一个范围内的键值数量(通常由一个给定的最小度数t确定)。
4. 子树数量:如果一个节点包含n个键,必然包含n+1个子节点。
5. 有序性:每个节点中的键值是按非递减顺序储存的。
3.诞生
B树由Rudolf Bayer和Edward M. McCreight在1972年发明。设计的目的是为了解决因大规模数据存储而产生的慢速磁盘访问问题。
4.优缺点
4.1.优点
1. 高效的查询和读写操作:通过减少I/O操作来提高性能。
2. 平衡性:自我平衡机制保证了高效的树结构。
3. 适合大规模数据:尤其适用于外存储设备(如硬盘)的数据存取,提高了搜索、插入、删除等操作的速度。
4.2.缺点
1. 实现复杂:相比其他基础数据结构,B树的实现逻辑相对复杂。
2. 占用更多存储空间:为了保持平衡性,需要额外的内部节点和子节点指针。
3. 维护成本高:在插入和删除操作中需要较多的旋转和分裂操作。
5.应用场景
1. 数据库索引
2. 文件系统(如NTFS)
3. 数据库管理系统(DBMS)
4. 内存缓冲区替换算法
5. 搜索引擎索引
6. 电子书阅读器(如Kindle)的索引
7. 存储系统的元数据管理
8. 版本控制系统
9. 多级缓存
10. 科学计算数据库
6.C语言中的B树实现例子
以下是一个简单的B树实现示例代码:
#include <stdio.h>
#include <stdlib.h>// 定义B树的最小度数 (最低范围)
#define T 3typedef struct BTreeNode
{int keys[2 * T - 1]; // minimum degreestruct BTreeNode *C[2 * T]; // child pointersint n; // current number of keysint leaf; // is true if leaf node
} BTreeNode;//创建新B-树节点
BTreeNode* createNode(int t, int leaf)
{BTreeNode* newNode = (BTreeNode*) malloc(sizeof(BTreeNode));newNode->leaf = leaf;newNode->n = 0;return newNode;
}//遍历B-树
void traverse(BTreeNode* root)
{if (root == NULL) return;int i;for (i = 0; i < root->n; i++) {if (root->leaf == 0) traverse(root->C[i]);printf(" %d", root->keys[i]);}if (root->leaf == 0) traverse(root->C[i]);
}//在B-树中搜索关键字
BTreeNode* search(BTreeNode* root, int k)
{int i = 0;while (i < root->n && k > root->keys[i]) i++;if (root->keys[i] == k) return root;if (root->leaf == 1) return NULL;return search(root->C[i], k);
}//拆分完整节点的子节点
void splitChild(BTreeNode* x, int i, BTreeNode* y)
{BTreeNode* z = createNode(y->leaf, T);z->n = T - 1;for (int j = 0; j < T - 1; j++) z->keys[j] = y->keys[j + T];if (!y->leaf){for (int j = 0; j < T; j++) z->C[j] = y->C[j + T];}y->n = T - 1;for (int j = x->n; j >= i + 1; j--) x->C[j + 1] = x->C[j];x->C[i + 1] = z;for (int j = x->n - 1; j >= i; j--) x->keys[j + 1] = x->keys[j];x->keys[i] = y->keys[T - 1];x->n = x->n + 1;
}//在非完整节点中插入新密钥
void insertNonFull(BTreeNode* x, int k)
{int i = x->n - 1;if (x->leaf == 1) {while (i >= 0 && x->keys[i] > k) {x->keys[i + 1] = x->keys[i];i--;}x->keys[i + 1] = k;x->n = x->n + 1;} else {while (i >= 0 && x->keys[i] > k) i--;if (x->C[i + 1]->n == 2 * T - 1) {splitChild(x, i + 1, x->C[i + 1]);if (x->keys[i + 1] < k) i++;}insertNonFull(x->C[i + 1], k);}
}//在B-树中插入新键值
void insert(BTreeNode** root, int k)
{if (*root == NULL) {*root = createNode(1, T);(*root)->keys[0] = k;(*root)->n = 1;} else {if ((*root)->n == 2 * T - 1) {BTreeNode* s = createNode(0, T);s->C[0] = *root;splitChild(s, 0, *root);int i = 0;if (s->keys[0] < k) i++;insertNonFull(s->C[i], k);*root = s;} else {insertNonFull(*root, k);}}
}int main()
{BTreeNode* root = NULL;int keys[] = {10, 20, 5, 6, 12, 30, 7, 17};int n = sizeof(keys) / sizeof(keys[0]);for (int i = 0; i < n; i++) {insert(&root, keys[i]);}printf("Traversal of constructed B-Tree: ");traverse(root);int k = 6;(search(root, k) != NULL) ? printf("\nPresent") : printf("\nNot Present");k = 15;(search(root, k) != NULL) ? printf("\nPresent") : printf("\nNot Present");return 0;
}7.总结
B树是一种重要的平衡树数据结构,具有高效的插入、删除和查找操作。广泛应用于数据库系统和文件系统中,由于其自平衡特性,使得其在处理大规模数据时表现出色。实现B树需要深入理解其复杂的结构及操作。上述示例代码展示了B树的基本插入和查找操作,提供了一个简单的实现参考。
相关文章:

数据结构之B数
目录 1.概述 2.特点 3.诞生 4.优缺点 4.1.优点 4.2.缺点 5.应用场景 6.C语言中的B树实现例子 7.总结 1.概述 B树(B-tree)是一种自平衡的树数据结构,广泛应用于数据库和文件系统中,以便高效地进行顺序读取、写入以及查找…...

计算机基础必须知道的76个常识!沈阳计算机软件培训
01 信息技术是指人们获取、存储、传递、处理、开发和利用信息资源的相关技术。 02 1、计算机的特点: (1)运算速度快 (2)存储容量大 (3)通用性强 (4)工作自动化 &…...

7,KQM模块的驱动
1,查资料,查模块的通信接口(单片机和模块之间采用什么方式通信)硬件接口,驱动方式(串口驱动用串口发送接收PC10,PC11) 只用了三个脚:VCC GND T&…...

软件验收测试报告模版分享,如何获取专业的验收测试报告?
软件验收测试报告是对软件开发过程中的最后一步确认,通过对软件进行全面、系统的检查和测试,形成一份详细的报告,以评估软件是否满足用户需求和设计要求。验收测试报告起到了非常重要的作用,不仅可以帮助开发者了解软件开发的质量…...
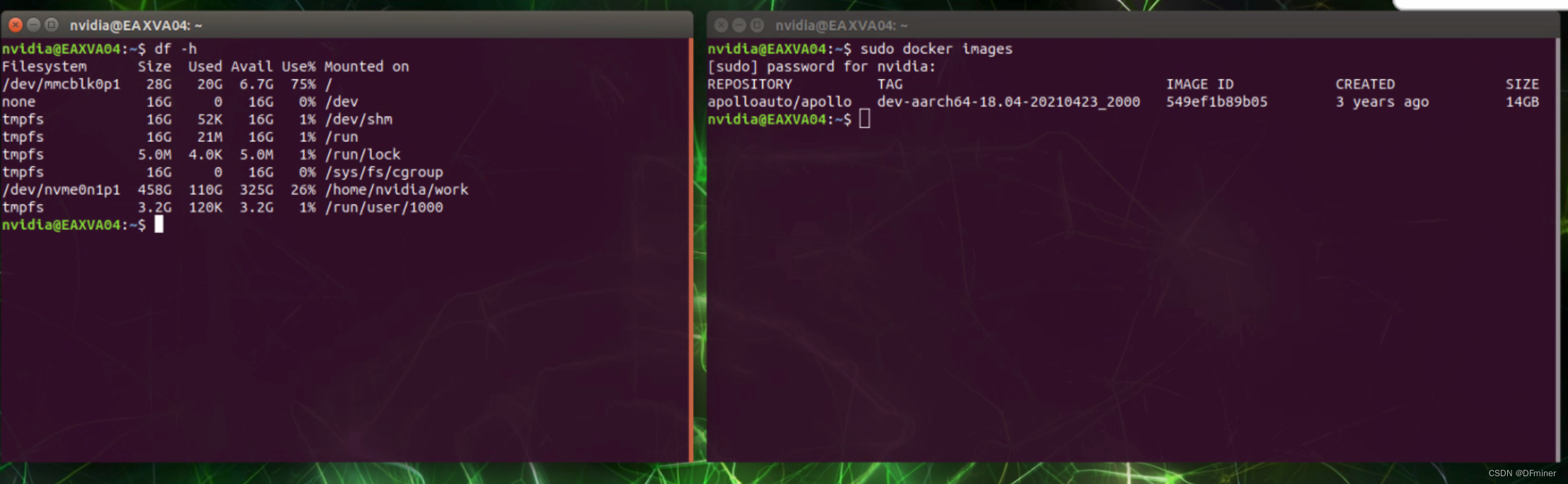
【arm扩容】docker load -i tar包 空间不足
背景: 首先我在/home/nvidia/work下导入了一些镜像源码tar包。然后逐个load进去。当我 load -i dev-aarch64-18.04-20210423_2000.tar包的时候,出现 Error processing tar file(exit status 1): write /9818cf5a7cbd5a828600d9a4d4e62185a7067e2a6f2ee…...

基于PID的直流电机自动控制系统的设计【MATLAB】
摘 要 本文在广泛查阅资料,了解直流电机特性的基础上,对直流电机的控制原理进行了的研究,设计了一款基于PID控制器的简单直流电机自动控制系统。 首先,分析了直流电机的应用背景和发展现状,对直流电机的工作原理和数学…...

MySQL----事务
MySQL 事务主要用于处理操作量大,复杂度高的数据。比如,在学校管理系统中,我们删除一个学生,既需要删除学生的基本资料,也要删除和该学生相关的信息,如班级,考试成绩等等,这样&#…...
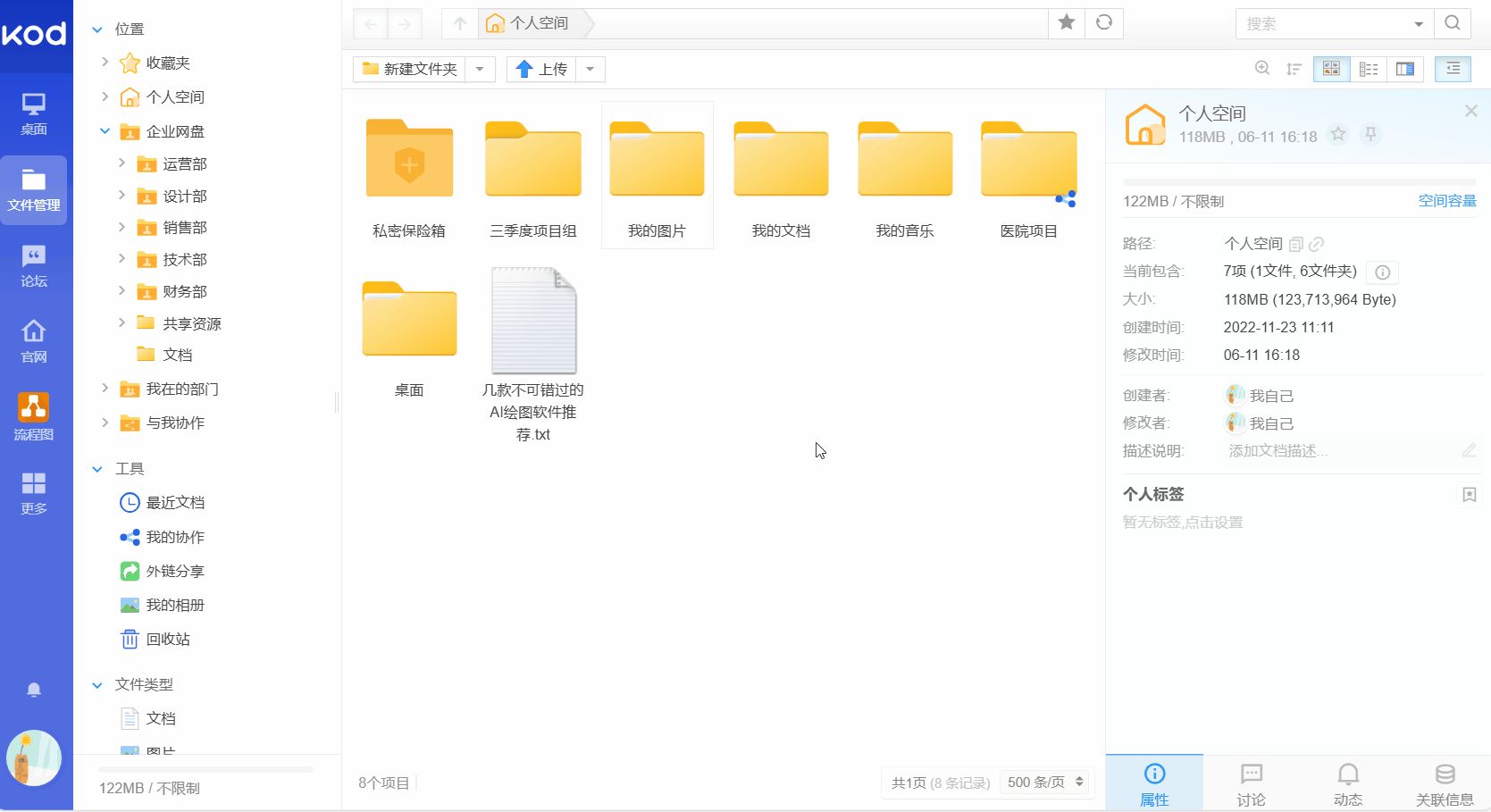
客观评价,可道云teamOS搭建的企业网盘,如Windows本地电脑一般的使用体验真的蛮不错
不管是企业网盘还是私有网盘,简单易用一直是我比较在意的。快速能上手使用,甚至不需要习惯一套新的操作逻辑,代表着不需要学习适应,能够迅速投入正常使用。 在这个过程中,可道云teamos以其Windows电脑般的流畅体验&am…...

当页面中有多个echarts图表的时候,resize不生效的修改方法
一、本来的代码 var myChart1 this.$echarts.init(document.getElementById(‘xxxx’)); let option {}; myChart1.setOption(option); setTimeout(function () {window.onresize function () {myChart1.resize();} }, 200) 二、修改后的代码 var myChart1 this.$echart…...

connect-caption-and-trace——用于共同建模图像、文本和人类凝视轨迹预测
介绍 论文地址:https://arxiv.org/abs/2105.05964 源码地址:https://github.com/facebookresearch/connect-caption-and-trace 在过去,计算机视觉和自然语言处理领域的模型和算法的发展只有偶尔的重叠,但近年来,这两…...

iOS API方法弃用警告说明及添加
一、常见系统方法警告或说明释义 NS_DEPRECATED_IOS(6_0, 8_0) 释义:iOS用;且在6.0被引用,将在8.0后废弃此方法。NS_DEPRECATED(6_0, 6_6, 8_0, 8_8) 释义:MacOS与iOS中都可用;但Mac系统中是在6.0被引用,6…...
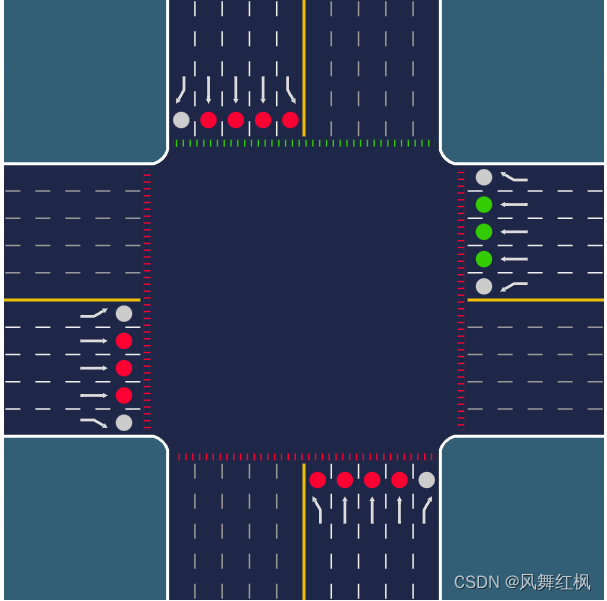
canvas绘制红绿灯路口(二)
系列文章 canvas绘制红绿灯路口(一) 无图不欢,先上图 优化项: 一:加入人行道红绿信号 二:加入专用车道标识(无方向标识时采用专用车道标识) 三:东南西北四项路口优化绘…...

Semantic Kernel 直接调用本地大模型与阿里云灵积 DashScope
本文主要介绍如何在无需网关,无需配置 HttpClient 的情况下,使用 Semantic Kernel 直接调用本地大模型与阿里云灵积 DashScope 等 OpenAI 接口兼容的大模型服务。 1. 背景 一直以来,我们都在探索如何更好地利用大型语言模型(LLM&…...

【人工智能】深度解读 ChatGPT基本原理
ChatGPT是OpenAI开发的一种基于人工智能技术的自然语言处理工具,它代表了自然语言处理(NLP)技术的前沿进展。ChatGPT的基本原理建立在一系列先进技术和方法之上,主要包括GPT(Generative Pre-trained Transformer&#…...

【教程】2024年如何快速提取爆款视频的视频文案?
关于如何提取爆款视频的视频文案,很朋友都不是很清楚,今天小编就带大家了解一下,希望这个知识点对大家有所帮助。 剪辑工作者有剪映、arctime、视频字幕等,但唯独编辑工作者或者编导没用直接提取视频文案的工具今天就说说可直接在…...

【MySQL连接器(Python)指南】02-MySQL连接器(Python)版本与实现
文章目录 前言MySQL连接器(Python)版本MySQL连接器(Python)实现总结前言 MySQL连接器(Python),用于让Python程序能够访问MySQL数据库。要想让Python应用程序正确高效地使用MySQL数据,就需要深入了解MySQL连接器的特性和使用方法。 MySQL连接器(Python)版本 下表总结了可用的…...

Vim入门教程
Vim是一个高度可配置的文本编辑器,用于创建和修改各种类型的文本文件。以下是一些基本的Vim使用示例,展示如何在Vim中进行编辑和操作。 1. 打开和保存文件 打开一个名为example.txt的文件: vim example.txt 打开多个文件,使用大…...
机器学习课程复习——隐马尔可夫
不考计算题 Q:概率图有几种结构? 条件独立性的公式? 顺序结构发散结构汇总结构Q:隐马尔可夫模型理解? 概念 集合:状态集合、观测集合 序列:状态序列、观测序列...

大数据-数据分析初步学习,待补充
参考视频:数据分析只需3小时从入门到进阶(up亲身实践)_哔哩哔哩_bilibili 数据指标: 对当前业务有参考价值的统计数据 分类:用户数据,业务数据,行为数据 用户数据 存量: DAU&#…...

微服务为什么使用RPC而不使用HTTP通信
微服务架构中使用RPC(Remote Procedure Call)而不是HTTP通信,主要是因为RPC在某些方面相比HTTP具有显著的优势。以下是一些关键原因: 性能: RPC通常比HTTP性能更高。RPC协议可以使用二进制序列化格式(如gRP…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
