【机器学习】线性回归:从基础到实践的深度解析


🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础
💫个人格言: "如无必要,勿增实体"

文章目录
- 线性回归:从基础到实践的深度解析
- 引言
- 一、线性回归基础
- 1.1 定义与目的
- 1.2 简单线性回归
- 1.3 多元线性回归
- 二、数学原理
- 2.1 最小二乘法
- 2.2 模型评估
- 三、实现方法
- 3.1 手动实现
- 3.2 利用库函数
- 四、实际应用中的考虑
- 4.1 特征选择与工程
- 4.2 正则化
- 4.3 模型评估与调优
- 五、总结与展望
线性回归:从基础到实践的深度解析

引言
线性回归作为统计学习和机器学习领域的基石之一,自19世纪末由Francis Galton和Carl Pearson提出以来,一直是数据分析、预测建模不可或缺的工具。它通过建立输入特征与连续目标变量之间的线性关系模型,为我们提供了一种理解和预测世界现象的强大手段。本文将深入浅出地介绍线性回归的基本概念、数学原理、实现方法以及在实际应用中的注意事项,力求为读者构建一个全面而深刻的理解框架。
一、线性回归基础
1.1 定义与目的
线性回归(Linear Regression)是一种预测分析模型,其基本思想是利用一个或多个自变量(输入特征)来预测或解释一个连续型因变量(目标变量)。简而言之,线性回归试图找到一个最佳拟合直线(或多维空间中的超平面),使得所有数据点到该直线的偏差平方和最小。
1.2 简单线性回归
简单线性回归是最基础的形式,仅涉及一个自变量 x x x和一个因变量 y y y。其模型可以表示为:
y = β 0 + β 1 x + ϵ y = \beta_0 + \beta_1x + \epsilon y=β0+β1x+ϵ
其中, β 0 \beta_0 β0是截距项, β 1 \beta_1 β1是斜率, ϵ \epsilon ϵ是误差项,反映了数据中的随机波动。
1.3 多元线性回归
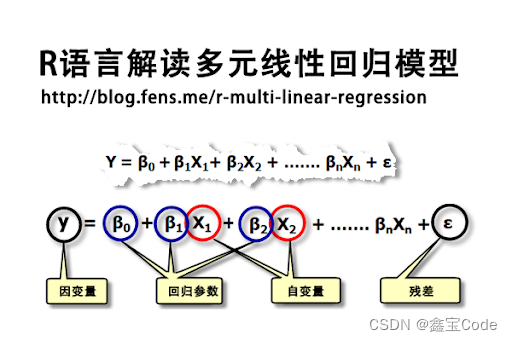
当存在两个或更多自变量时,模型扩展为多元线性回归:
y = β 0 + β 1 x 1 + β 2 x 2 + . . . + β n x n + ϵ y = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_nx_n + \epsilon y=β0+β1x1+β2x2+...+βnxn+ϵ
这里, x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn代表多个自变量, β 1 , β 2 , . . . , β n \beta_1, \beta_2, ..., \beta_n β1,β2,...,βn是各自变量的系数。
二、数学原理
2.1 最小二乘法
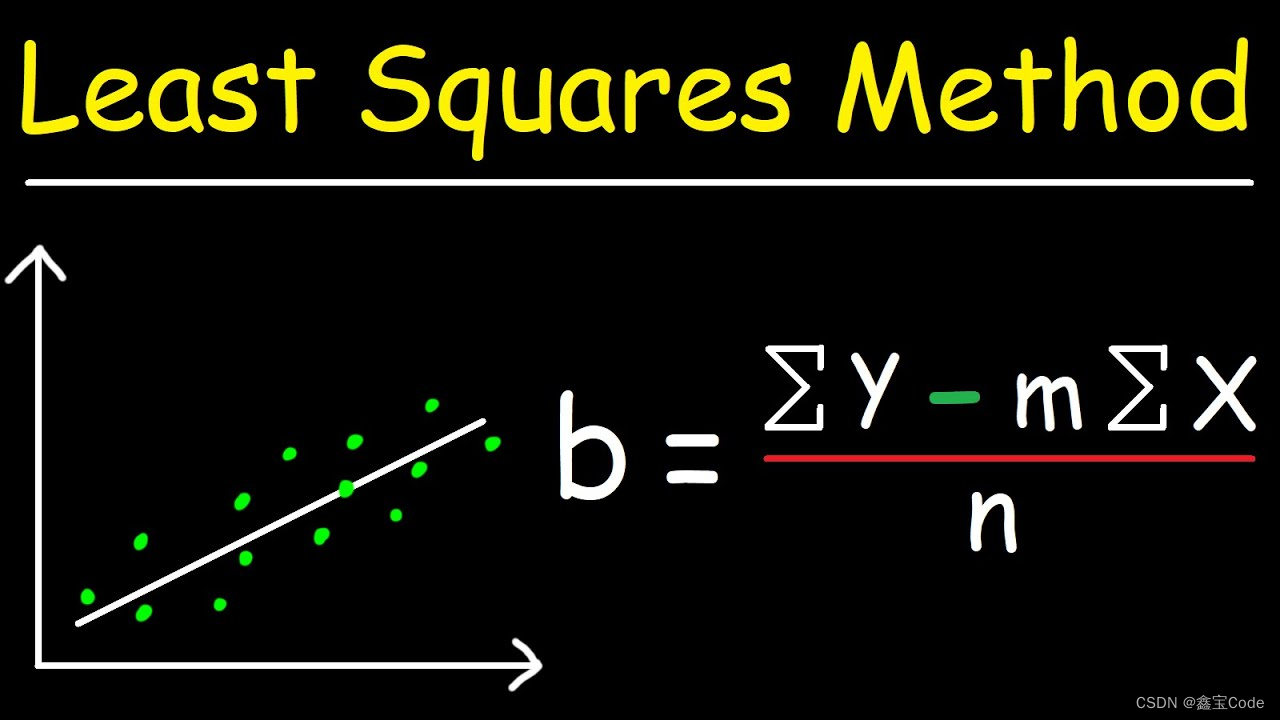
最小二乘法是线性回归中常用的参数估计方法。其核心思想是通过最小化残差平方和(RSS: Residual Sum of Squares)来确定模型参数:
RSS = ∑ i = 1 n ( y i − ( β 0 + β 1 x i 1 + . . . + β n x i n ) ) 2 \text{RSS} = \sum_{i=1}^{n}(y_i - (\beta_0 + \beta_1x_{i1} + ... + \beta_nx_{in}))^2 RSS=i=1∑n(yi−(β0+β1xi1+...+βnxin))2
通过求导数并令导数等于零,可以解得参数 β 0 , β 1 , . . . , β n \beta_0, \beta_1, ..., \beta_n β0,β1,...,βn的最优值。
2.2 模型评估
- 均方误差(MSE):衡量预测值与真实值之间差异的平均程度。
- 决定系数(R²):表示模型解释的变异量占总变异量的比例,值越接近1说明模型拟合度越高。
三、实现方法
3.1 手动实现
手动实现线性回归包括数据预处理、梯度下降或正规方程求解等步骤。以梯度下降为例,迭代更新参数直到收敛:
β j : = β j − α ∂ ∂ β j RSS \beta_j := \beta_j - \alpha \frac{\partial}{\partial \beta_j}\text{RSS} βj:=βj−α∂βj∂RSS
其中, α \alpha α是学习率,控制每次迭代的步长。
3.2 利用库函数
在Python中,可以使用scikit-learn库轻松实现线性回归:
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)
四、实际应用中的考虑
4.1 特征选择与工程
- 相关性分析:筛选与目标变量高度相关的特征。
- 多项式特征:对非线性关系进行转换,增强模型表达能力。
4.2 正则化
- L1正则化(Lasso回归):倾向于产生稀疏解,可用于特征选择。
- L2正则化(Ridge回归):减少模型复杂度,避免过拟合。

4.3 模型评估与调优
- 交叉验证:确保模型泛化性能。
- 网格搜索:自动寻找最佳超参数组合。
五、总结与展望
线性回归以其简单直观、易于理解和实现的特点,在金融、医疗、社会科学等多个领域发挥着重要作用。然而,面对复杂的数据关系,非线性模型如支持向量机、神经网络等可能提供更好的解决方案。未来,结合深度学习技术的线性回归变体,以及在大数据环境下的高效实现,将继续推动这一经典模型的发展,拓展其应用边界。
通过本文的介绍,希望能帮助读者建立起线性回归的坚实理论基础,并激发进一步探索和应用的兴趣。随着技术的不断进步,线性回归及其衍生方法将持续为解决实际问题提供强大的支持。


相关文章:

【机器学习】线性回归:从基础到实践的深度解析
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 线性回归:从基础到实践的深度解析引言一、线性回归基础1.1 定义与目…...

短视频开源项目MoneyPrinterTurbo:AI副业搞起来,视频制作更轻松!
目录 引言一、MoneyPrinterTurbo简介二、MoneyPrinterTurbo的核心功能三、MoneyPrinterTurbo的未来发展四、MoneyPrinterTurbo与AI副业五、部署实践1、克隆代码2、创建虚拟环境3、安装依赖4、安装好 ImageMagick5、端口映射6、启动Web界面7、模型配置8、填写主题9、视频生成10、…...
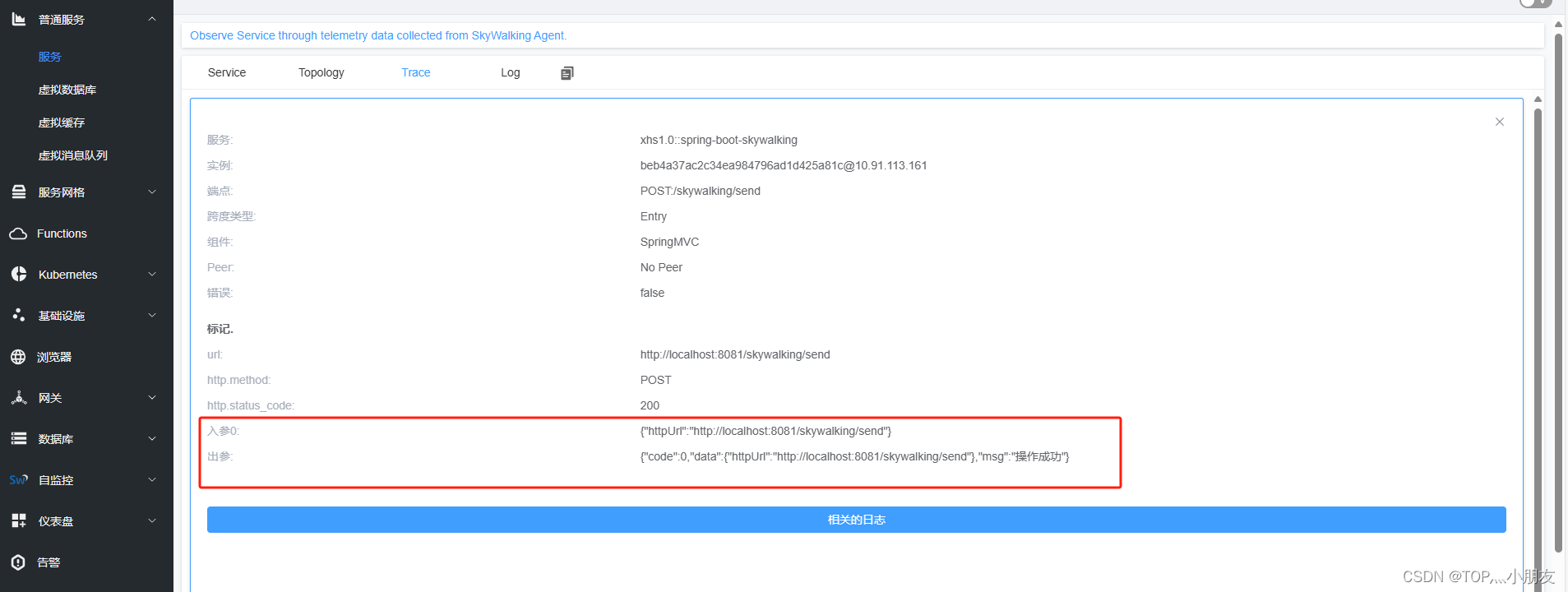
【JAVA】SpringBoot + skywalking 将接口的入参、出参、异常等信息上报到skywalking 链路追踪服务器上
【JAVA】SpringBoot skywalking 将接口的入参、出参、异常等信息上报到skywalking 链路追踪服务器上 1.下载SkyWalking APM https://skywalking.apache.org/downloads/ jdk8 不支持 SkyWalking APM 9.3.0以上版本,所以这里我们下载 9.3.0版本 2.下载 Java Agent …...

[xmake]构建静态库和动态库
xmake 静态库和动态库 在xmake中创建静态库和动态库的方法非常相似。以下是创建静态库和动态库的基本步骤: 创建xmake工程文件(xmake.lua)。 配置工程属性,包括工程名、版本等。 添加源代码文件到工程中。 设置是创建静态库还…...

功能测试 之 单模块测试----轮播图、登录、注册
单功能怎么测? 需求分析 拆解测试点 编写用例 1.轮播图 (1)需求分析 位置:后台--页面--广告管理---广告列表(搜索index页面增加广告位2) 操作完成后需要点击admin---更新缓存,前台页面刷新生效 (2)拆解…...

MyBatis-PageHelper 源码解说
归档 GitHub: MyBatis-PageHelper-源码解说 总说明 源码仓库: https://github.com/pagehelper/Mybatis-PageHelper克隆:git clone https://github.com/pagehelper/Mybatis-PageHelper.git切分支(tag):git checkout m…...

基于uni-app和图鸟UI的智慧校园圈子小程序开发实践
摘要: 随着教育信息化和“互联网教育”的快速发展,智慧校园建设已成为推动校园管理现代化、提高教育教学质量的重要手段。本文介绍了基于uni-app和图鸟UI开发的智慧校园圈子小程序,旨在通过一站式服务、个性化定制、数据互通和安全可靠等特点…...

STM32 keil工程移植到Visual Studio Code环境中编译
1、GCC Vscode 搭建 STM32 开发环境 GCC Vscode 搭建 STM32 开发环境(一)- 环境部署 - 知乎 (zhihu.com) 2、在原有keil工程下找到原本CUBEMX生成的.ioc工程文件 3、将.ioc文件复制一个新的文件夹下双击打开工程,将IDE选为Makefile&…...

细说CountDownLatch
CountDownLatch是Java中提供的一个同步辅助类,它允许一个或多个线程等待其他线程完成操作。在面试中,面试官经常会询问候选人是否在实际项目中使用过CountDownLatch,以评估其对多线程编程和并发控制的理解和经验。本文将详细介绍CountDownLat…...

java-克隆应用
5.2 创建复杂对象 对于某些复杂对象,通过克隆来创建其副本比通过构造函数创建新实例更加高效。例如,当对象包含大量字段或需要进行复杂初始化时,克隆可以显著提高性能。 java 复制代码 class ComplexObject implements Cloneable { private …...
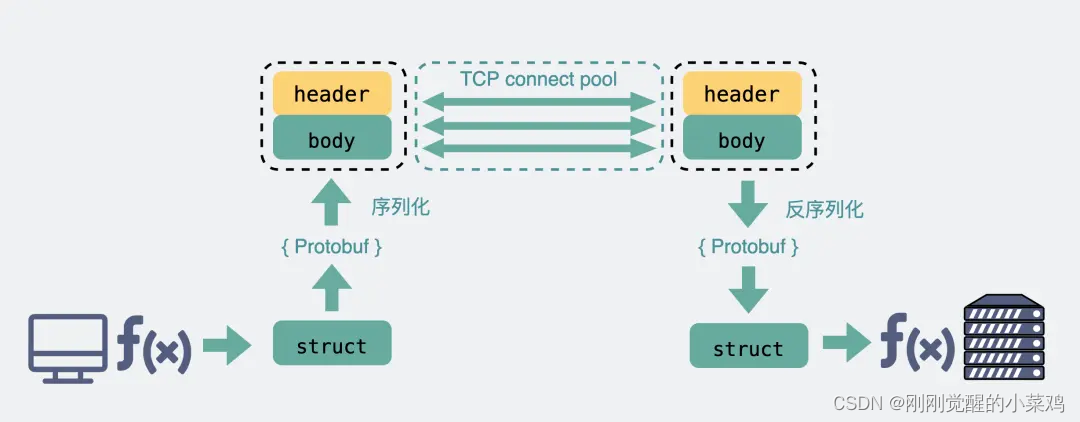
RPC协议
3.8 既然有 HTTP 协议,为什么还要有 RPC 假设我们需要在 A 电脑的进程发一段数据到 B 电脑的进程,我们一般会在代码里使用 Socket 进行编程。 这时候,我们可选项一般也就 TCP 和 UDP 二选一。TCP 可靠,UDP 不可靠。 类似下面这…...

医疗器械3D全景展会在线漫游创造数字化时代的展览新篇章
在数字化浪潮的引领下,VR虚拟网上展会正逐渐成为企业展示品牌实力、吸引潜在客户的首选平台。我们与广交会携手走过三年多的时光,凭借优质的服务和丰富的经验,赢得了客户的广泛赞誉。 面对传统展会活动繁多、企业运营繁忙的挑战,许…...

IP_Endpoint类型在CAPL中的使用
在使用TCP/IP协议栈通信时,创建Socket套接字调用接口函数实现通信的整个过程成为一种主流且便捷的方式。在CAPL中,Client需要创建TCP或UDP套接字,绑定自己的IP地址和一个端口号,作为自己的通信端点。 on key c {clientsocket = tcpOpen(ipGetAddressAsNumber("192.16…...

数据资产与用户体验优化:深入挖掘用户数据,精准分析用户需求与行为,优化产品与服务,提升用户体验与满意度,打造卓越的用户体验,赢得市场认可
一、引言 在数字化时代,数据已经成为企业最宝贵的资产之一。通过深入挖掘和分析用户数据,企业能够精准把握用户需求和行为,从而优化产品与服务,提升用户体验和满意度。这不仅有助于企业在激烈的市场竞争中脱颖而出,还…...

基于TCAD与紧凑模型结合方法探究陷阱对AlGaN/GaN HEMTs功率附加效率及线性度的影响
来源:Investigation of Traps Impact on PAE and Linearity of AlGaN/GaN HEMTs Relying on a Combined TCAD–Compact Model Approach(TED 24年) 摘要 本文提出了一种新型建模方法,用于分析GaN HEMTs的微波功率性能。通过结合工…...

具身智能概念
具身智能作为人工智能发展的一个重要分支,伴随着大模型技术的爆发与硬件成本的降低,即软硬件技术走向成熟,正在成为广泛关注的热门,一时之间,具身智能机器人也成为了科技界新的风向标。 什么是具身智能? …...

C++ 43 之 自增运算符的重载
#include <iostream> #include <string> using namespace std;class MyInt{friend ostream& operator<< (ostream& cout , MyInt& int1); public:MyInt(){this->m_num 0;}// 前置自增: 成员函数实现运算符的重载 返回的是 引用&a…...

计算机网络:1概述、2物理层
目录 概述因特网网络、互连网(互联网)与因特网的区别与关系因特网发展的三个阶段因特网服务提供者(Internet Service Provider,ISP)因特网的标准化工作因特网的管理结构 三种交换电路交换分组交换报文交换 计算机网络性…...
【Ardiuno】实验使用ESP32接收电脑发送的串口数据(图文)
使用ESP32可以非常方便的与电脑进行串口通讯,一般我们可以用串口接收ESP32的输出作为调试使用,今天我们再来实验一下从电脑端向ESP32单片机发送数据。 发送数据程序代码: void setup() {Serial.begin(9600); }void loop() { if(Serial.ava…...

思科ospf+rip重发布配置命令
——————————————————————————————————————————— 基础配置 R1 Router>en #进入配置模式 Router#conf #进入配置模式 Router(config)#h…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...
