图论算法学习
图论
- dfs是可一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。
- bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
DFS
如何在二维矩阵中使用 DFS 搜索呢?如果你把二维矩阵中的每一个位置看做一个节点,这个节点的上下左右四个位置就是相邻节点,那么整个矩阵就可以抽象成一幅网状的「图」结构。
DFS (Depth-First Search) 是一种图遍历算法,用于探索或搜索图或树的节点。该算法从起始节点开始,尽可能深地探索每个分支,直到遇到没有未探索邻居的节点,然后回溯到上一个未探索的节点,并继续探索其他分支。这个过程一直持续到所有节点都被访问为止。
因为二维矩阵本质上是一幅「图」,所以遍历的过程中需要一个visited 布尔数组防止走回头路,如果你能理解下面这段代码,那么搞定所有岛屿系列题目都很简单。
二维矩阵遍历框架
// 二叉树遍历框架
void traverse(TreeNode root) {traverse(root.left);traverse(root.right);
}
//-------------------------------
// 二维矩阵遍历框架
void dfs(int[][] grid, int i, int j, boolean[][] visited) {//行和列int m = grid.length, n = grid[0].length;if (i < 0 || j < 0 || i >= m || j >= n) {// 超出索引边界return;}if (visited[i][j]) {// 已遍历过 (i, j)return;}// 进入节点 (i, j)visited[i][j] = true;dfs(grid, i - 1, j, visited); // 上dfs(grid, i + 1, j, visited); // 下dfs(grid, i, j - 1, visited); // 左dfs(grid, i, j + 1, visited); // 右
}岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
class Solution {// 主函数,计算岛屿数量int numIslands(char[][] grid) {int res = 0;int m = grid.length, n = grid[0].length;// 遍历 gridfor (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (grid[i][j] == '1') {// 每发现一个岛屿,岛屿数量加一res++;// 然后使用 DFS 将岛屿淹了 与1相连的所有1 变为零 集体是一个岛屿dfs(grid, i, j);// 上下左右都淹了}}}return res;}// 从 (i, j) 开始,将与之相邻的陆地都变成海水void dfs(char[][] grid, int i, int j) {int m = grid.length, n = grid[0].length;// 参数是否正常if (i < 0 || j < 0 || i >= m || j >= n) {// 超出索引边界return;}if (grid[i][j] == '1') {grid[i][j] = '0';} else {return;}// 淹没上下左右的陆地dfs(grid, i + 1, j);dfs(grid, i, j + 1);dfs(grid, i - 1, j);dfs(grid, i, j - 1);}
}为什么每次遇到岛屿,都要用 DFS 算法把岛屿「淹了」呢?主要是为了省事,避免维护 visited 数组。
因为 dfs 函数遍历到值为 0 的位置会直接返回,所以只要把经过的位置都设置为 0,就可以起到不走回头路的作用。
单词搜索(DFS算法) (回溯算法)
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
- grid.length 返回 grid 数组的长度,即行数。
- grid[0].length 返回 grid 数组的第一行的长度,即列数。
class Solution {boolean found = false;public boolean exist(char[][] board, String word) {int m = board.length, n = board[0].length;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {dfs(board, i, j, word, 0);if (found) {return true;}}}return false;}// 从 (i, j) 开始向四周搜索,试图匹配 word[p..]void dfs(char[][] board, int i, int j, String word, int p) {if (p == word.length()) {// 整个 word 已经被匹配完,找到了一个答案found = true;return;}if (found) {// 已经找到了一个答案,不用再搜索了return;}int m = board.length, n = board[0].length;if (i < 0 || j < 0 || i >= m || j >= n) {return;}if (board[i][j] != word.charAt(p)) {return;}// 已经匹配过的字符,我们给它添一个负号作为标记,避免走回头路board[i][j] = (char)(-board[i][j]);// word[p] 被 board[i][j] 匹配,开始向四周搜索 word[p+1..]dfs(board, i + 1, j, word, p + 1);dfs(board, i, j + 1, word, p + 1);dfs(board, i - 1, j, word, p + 1);dfs(board, i, j - 1, word, p + 1);board[i][j] = (char)(-board[i][j]);}
}BFS
广搜(bfs)是一圈一圈的搜索过程,和深搜(dfs)是一条路跑到黑然后再回溯。
广搜的搜索方式就适合于解决两个点之间的最短路径问题。
从起点出发,每次都尝试访问同一层的节点,如果同一层都访问完了,再访问下一层,最后广度优先搜索找到的路径就是从起点开始的最短合法路径。
使用队列
代码框架
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {Queue<Node> q; // 核心数据结构Set<Node> visited; // 避免走回头路q.offer(start); // 将起点加入队列visited.add(start);while (q not empty) {int sz = q.size();/* 将当前队列中的所有节点向四周扩散 */for (int i = 0; i < sz; i++) {Node cur = q.poll();/* 划重点:这里判断是否到达终点 */if (cur is target)return step;/* 将 cur 的相邻节点加入队列 */for (Node x : cur.adj()) {if (x not in visited) {q.offer(x);visited.add(x);}}}}// 如果走到这里,说明在图中没有找到目标节点
}队列 q 就不说了,BFS 的核心数据结构;cur.adj() 泛指 cur 相邻的节点,比如说二维数组中,cur 上下左右四面的位置就是相邻节点;visited 的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要 visited。
二叉树的最小高度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
起点就是 root 根节点,终点就是最靠近根节点的那个「叶子节点」
class Solution {public int minDepth(TreeNode root) {if (root == null)return 0;Queue<TreeNode> q = new LinkedList<>();q.offer(root);// root 本身就是一层,depth 初始化为 1int depth = 1;while (!q.isEmpty()) {int sz = q.size();/* 将当前队列中的所有节点向四周扩散 */for (int i = 0; i < sz; i++) {TreeNode cur = q.poll();/* 判断是否到达终点 */if (cur.left == null && cur.right == null)return depth;/* 将 cur 的相邻节点加入队列 */if (cur.left != null)q.offer(cur.left);if (cur.right != null)q.offer(cur.right);}/* 这里增加步数 */depth++;}return depth;}
}腐烂的橘子
上下左右相邻的新鲜橘子就是该腐烂橘子尝试访问的同一层的节点,路径长度就是新鲜橘子被腐烂的时间。我们记录下每个新鲜橘子被腐烂的时间,最后如果单元格中没有新鲜橘子,腐烂所有新鲜橘子所必须经过的最小分钟数就是新鲜橘子被腐烂的时间的最大值。
- 一开始,我们找出所有腐烂的橘子,将它们放入队列,作为第 0 层的结点。
- 然后进行 BFS 遍历,每个结点的相邻结点可能是上、下、左、右四个方向的结点,注意判断结点位于网格边界的特殊情况。
- 由于可能存在无法被污染的橘子,我们需要记录新鲜橘子的数量。在 BFS 中,每遍历到一个橘子(污染了一个橘子),就将新鲜橘子的数量减一。如果 BFS 结束后这个数量仍未减为零,说明存在无法被污染的橘子。
- Count 统计多少橘子 ,
class Solution {public int orangesRotting(int[][] grid) {// 边界 长宽int M = grid.length;int N = grid[0].length;Queue<int[]> queue = new LinkedList<>();//每一个元素都是一个一维数组 行和列// count 表示新鲜橘子的数量int count = 0; // 遍历二维数组 找出所有的新鲜橘子和腐烂的橘子for (int r = 0; r < M; r++) {for (int c = 0; c < N; c++) {// 新鲜橘子计数if (grid[r][c] == 1) {count++;// 腐烂的橘子就放进队列} else if (grid[r][c] == 2) {// 缓存腐烂橘子的坐标queue.add(new int[]{r, c});}}}// round 表示腐烂的轮数,或者分钟数int round = 0; // 如果有新鲜橘子 并且 队列不为空// 直到上下左右都触及边界 或者 被感染的橘子已经遍历完while (count > 0 && !queue.isEmpty()) {// BFS 层级 + 1round++;// 拿到当前层级的腐烂橘子数量, 因为每个层级会更新队列int n = queue.size();// 遍历当前层级的队列for (int i = 0; i < n; i++) {// 踢出队列(拿出一个腐烂的橘子)int[] orange = queue.poll();// 恢复橘子坐标int r = orange[0];int c = orange[1];// ↑ 上邻点 判断是否边界 并且 上方是否是健康的橘子if (r-1 >= 0 && grid[r-1][c] == 1) {// 感染它 grid[r-1][c] = 2;// 好橘子 -1 count--;// 把被感染的橘子放进队列 并缓存queue.add(new int[]{r-1, c});}// ↓ 下邻点 同上if (r+1 < M && grid[r+1][c] == 1) {grid[r+1][c] = 2;count--;queue.add(new int[]{r+1, c});}// ← 左邻点 同上if (c-1 >= 0 && grid[r][c-1] == 1) {grid[r][c-1] = 2;count--;queue.add(new int[]{r, c-1});}// → 右邻点 同上if (c+1 < N && grid[r][c+1] == 1) {grid[r][c+1] = 2;count--;queue.add(new int[]{r, c+1});}}}// 如果此时还有健康的橘子// 返回 -1// 否则 返回层级if (count > 0) {return -1;} else {return round;}}
}相关文章:

图论算法学习
图论 dfs是可一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,再换方向(换方向的过程就涉及到了回溯)。bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再…...

面试题——RabbitMQ
★1.如何保证消息的幂等性?(如何避免消息重复投递) 生产端: 在消息发送前,先查询数据库此消息是否被处理过。处理过则忽略、否则继续处理,并在处理完成后修改状态为已处理。 消费端: 每个消息都生成全局唯一ID或业务I…...

前端开发之浏览器垃圾回收机制
前端开发之浏览器垃圾回收机制 V8引擎,作为Chrome浏览器和Node.js等环境下的JavaScript运行引擎,其垃圾回收机制是确保高效内存管理的关键。 V8垃圾回收机制的深度解析与优化 V8 JavaScript引擎采用了高效的垃圾回收机制,其中核心的实现特…...

less-loader的less转成CSS的底层原理
在现代Web开发中,CSS预处理器如LESS极大地提高了编写样式的效率和灵活性。而less-loader作为webpack的一个加载器,用于将LESS文件转换为CSS文件。本文将深入探讨less-loader如何工作,从解析LESS文件到生成最终的CSS文件的底层原理。 工作流程…...

解锁Flutter中的ProcessResult:让外部命令执行变得轻松
介绍 在我们的编程世界中,有时候我们需要与外部系统或者命令行交互。这就像在一场迷宫中寻找出口一样,我们需要向迷宫的门口询问正确的道路。而在 Flutter 中,这个问路的过程就是通过 ProcessResult 来实现的。 为什么要使用 ProcessResult…...

第二十五篇——信息加密:韦小宝说谎的秘诀
目录 一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么? 四、总结五、升华 一、背景介绍 加密这件事,对于这个时代的我们来说非常重要,那么…...
Redis 主从复制+哨兵+集群
1、总结写在前面 Redis 集群 数据分片 高可用性 Redis 哨兵 主从复制 故障转移 2、主从复制 2.1、准备配置 查看docker 容器 ip docker inspect 容器id | grep IPAddressdocker inspect -f{{.Name}} {{.NetworkSettings.IPAddress}} $(docker ps -aq)修改配置文件 初始…...
cpolar:通过脚本自动更新主机名称和端口号进行内网穿透【免费版】
cpolar 的免费版经常会重新分配 HostName 和 Port,总是手动修改太过麻烦,分享一下自动更新配置文件并进行内网穿透的方法。 文章目录 配置 ssh config编写脚本获取 csrf_token打开登陆界面SafariChrome 设置别名 假设你已经配置好了服务器端的 cpolar。 …...
【Python日志模块全面指南】:记录每一行代码的呼吸,掌握应用程序的脉搏
文章目录 🚀一、了解日志🌈二、日志作用🌈三、了解日志模块⭐四、日志级别💥五、记录日志-基础❤️六、记录日志-处理器handler🎬七、记录日志-格式化记录☔八、记录日志-配置logger👊九、流程梳理 &#x…...
)
SpringBoot 多种优雅的线程池配置与使用(异步执行函数,反射机制,动态识别参数,有返回值)
想要明白生活你需要先经历它,而不是总在分析它。 —萨莉鲁尼 文章目录 前言一、@Async注解1. 概念2. 使用2.1 使用@EnableAsync启动函数异步支持2.2 不会异步执行的坑2.2.1 为什么内部调用不会异步执行?2.2.2 如何确保@Async方法异步执行?3. 配置线程池3.1 通过代码配置3.1.…...

ansible copy模块--持续创作中
copy模块用于将文件从ansible控制节点(管理主机)或者远程主机复制到远程主机上。其操作类似于scp(secure copy protocol)。 关键参数标红。 参数: src:(source:源) 要复制到远程…...
自学SAP是学习ECC版本还是S4版本?
很多人想学SAP,问我应该学ECC版本还是S4版本,我的建议如果你是自学的话,我个人建议使用ECC版本就行,因为这两个版本前台业务和后台配置的操作差异并不大,主要差异在于数据库的差异,前台业务操作和后台系统配…...
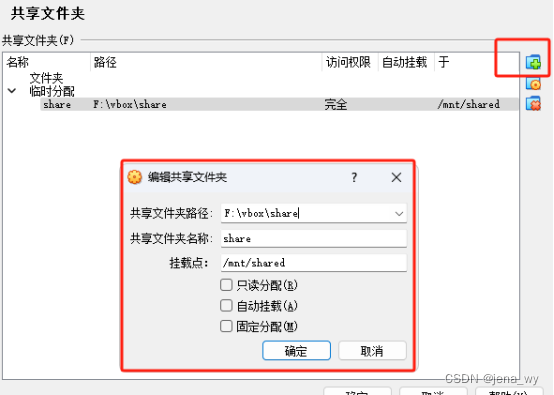
银河麒麟4.0.2安装带有opengl的Qt5.12.9
银河麒麟4.0.2下载地址:银河麒麟-银河麒麟(云桌面系统)-银河麒麟最新版下载v4.0.2-92下载站 VirtualBox:https://www.virtualbox.org/wiki/Downloads qt下载:Index of /archive/qt/5.12/5.12.9 1安装VirtualBox:网上教材比较多 1)安装完后安…...

django学习入门系列之第二点《浏览器能识别的标签3》
文章目录 列表表格往期回顾 列表 无序列表 <!-- <ul </ul> 无序列表 --> <ul><li> 内容1 </li><li> 内容2 </li><li> 内容3 </li><li> 内容4 </li> </ul>有序列表 <!-- <ol> &…...

git常见实用命令,简单上手操作
常用命令: 添加远程账号名称:git config --global user.name ‘’ 添加用户eamil:git config --global user.email ‘’ 初始化厂库:git init 新建文件夹:mkdir 文件夹名 新建文件:touch 文件名 查看…...
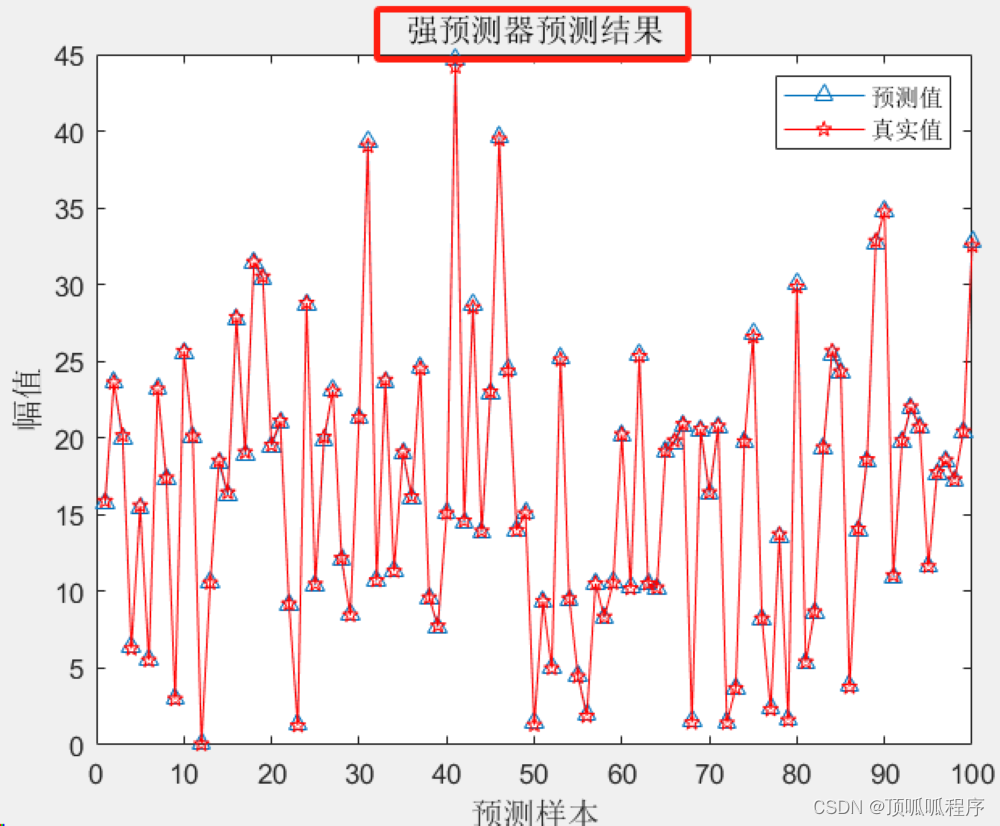
2-11 基于matlab的BP-Adaboost的强分类器分类预测
基于matlab的BP-Adaboost的强分类器分类预测,Adaboost是一种迭代分类算法,其在同一训练集采用不同方法训练不同分类器(弱分类器),并根据弱分类器的误差分配不同权重,然后将这些弱分类器组合成一个更强的最终…...

Neo4j图形数据库查询,Cypher语言详解
Cypher语言详解 Cypher是一种专为Neo4j图形数据库设计的声明式查询语言。它类似于SQL,但其设计目标是便于表达图数据库中常见的图形结构和操作。本文将详细介绍Cypher语言的基本语法、常见操作、高级功能以及使用Cypher进行图形数据分析的技巧。 1. Cypher的基本概…...
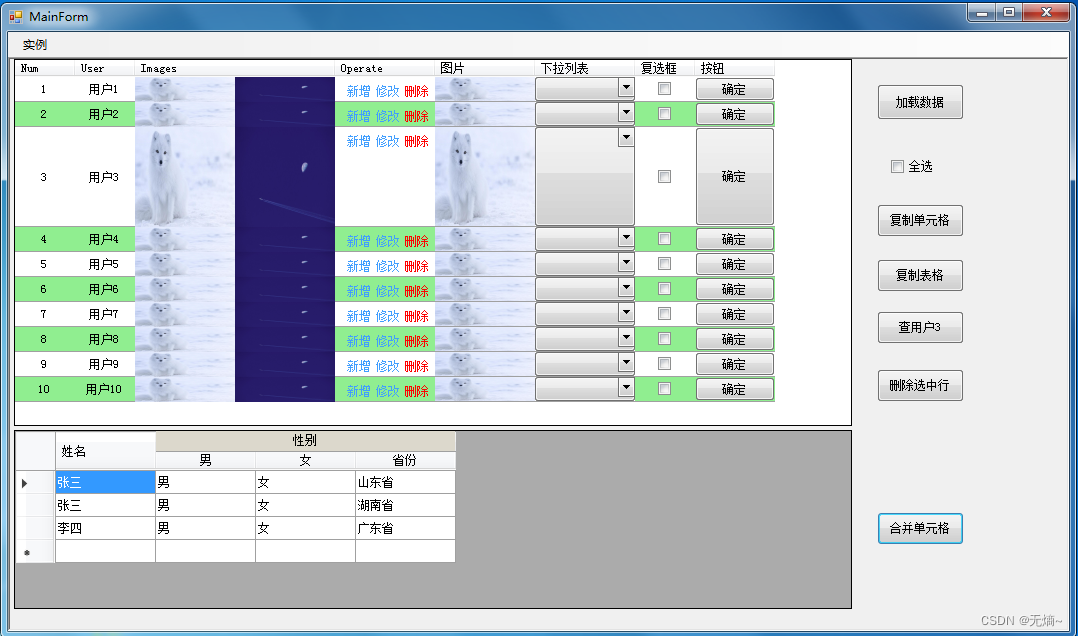
C# Winform Datagridview控件使用和详解
DataGridView 是一种以表格形式显示数据的控件,由Rows(行),Columns(列),Cells(单元格)构成。本实例将综合利用DataGridView的属性和事件,展示不同的表格风格数据和操作。包含: 添加Datagridview行,列数据设…...
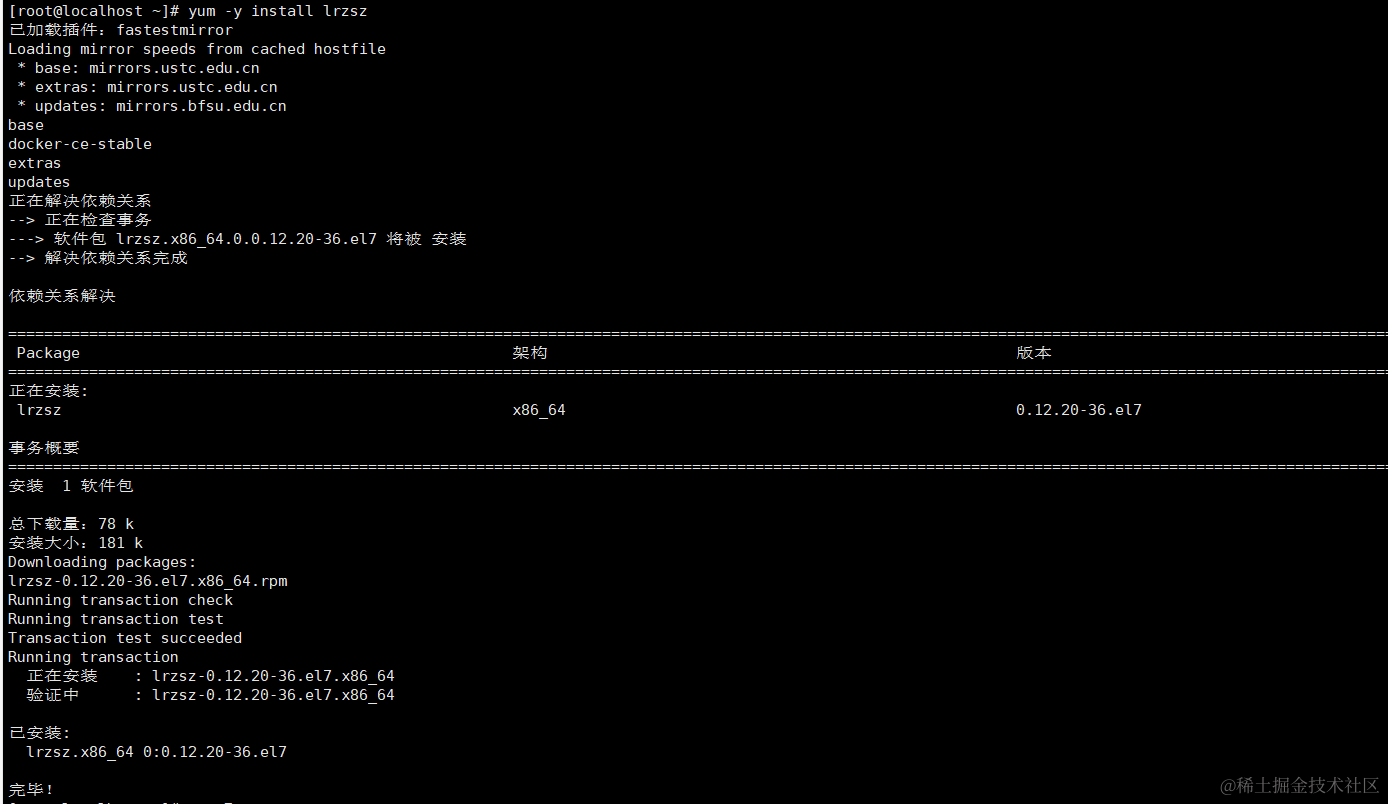
xshell传输文件速率为0
你们好,我是金金金。 场景 此时我通过xshell客户端上传文件,速率一直为0 解决 安装 yum -y install lrzsz 即可 这个工具主要提供 rz 和 sz 命令,用于通过 Zmodem 协议在本地计算机和远程服务器之间传输文件 编写有误还请大佬指正࿰…...
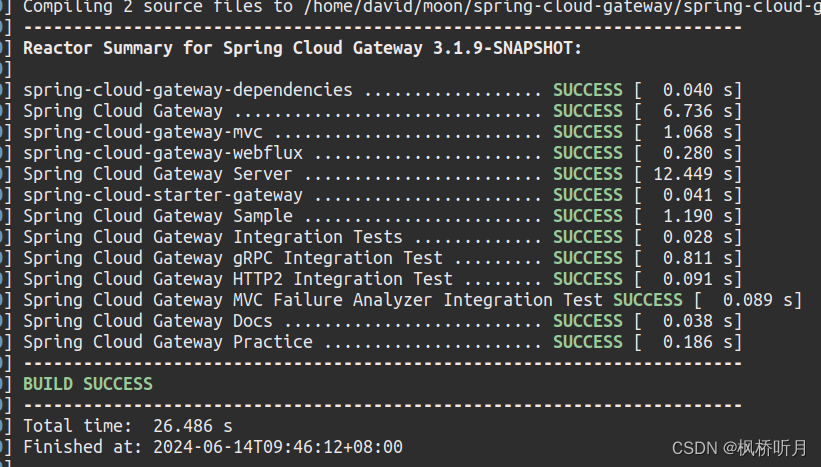
2.spring cloud gateway 源码编译
spring cloud gateway编译 1.编译 命令 mvn clean compile -U2.报错 报错信息 核心信息 [ERROR] Failed to execute goal org.apache.maven.plugins:maven-checkstyle-plugin:3.1.2:check (checkstyle-validation) on project spring-cloud-gateway-mvc: Failed during …...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
