(创新)基于VMD-CNN-BiLSTM的电力负荷预测—代码+数据
目录
一、主要内容:
二、运行效果:
三、VMD-BiLSTM负荷预测理论:
四、代码+数据下载:
一、主要内容:
本代码结合变分模态分解( Variational Mode Decomposition,VMD) 和卷积神经网络(Convolutional neural network, CNN)-双向长短时记忆神经网络( Bi-Long Short-Term Memory,Bi-LSTM) 算法,建立了一种短期负荷预测模型( VMD-CNN-BiLSTM) 。首先采用 VMD 技术将输入负荷数据分解为多个有限带宽的本征模态分量,分解结果表明了人们生产生活中不同的用电习惯,并且分离了数据中的噪声和信号,然后对每个模态分量建立 CNN-BiLSTM 神经网络进行预测,结合模型输出重构预测结果。其中,CNN用于提取负荷分量中的用电特征信息,BiLSTM用于提取负荷分量中的用电时序信息。
本代码基于Matlab平台,建立了VMD-CNN-BiLSTM模型进行负荷预测,并和传统的单一CNN-BiLSTM模型进行对比,充分说明本文所提方法的有效性。
-
注释详细,几乎每一关键行都有注释说明,适合小白起步学习
-
直接运行Main函数即可看到所有结果,使用便捷
-
编程习惯良好,程序主体标准化,逻辑清晰,方便阅读代码
-
附带一年365天的负荷数据,所有数据均采用Excel格式输入,替换数据方便,适合懒人选手.
-
100%原创,出图详细、丰富、美观,可直观查看运行效果
二、运行效果:
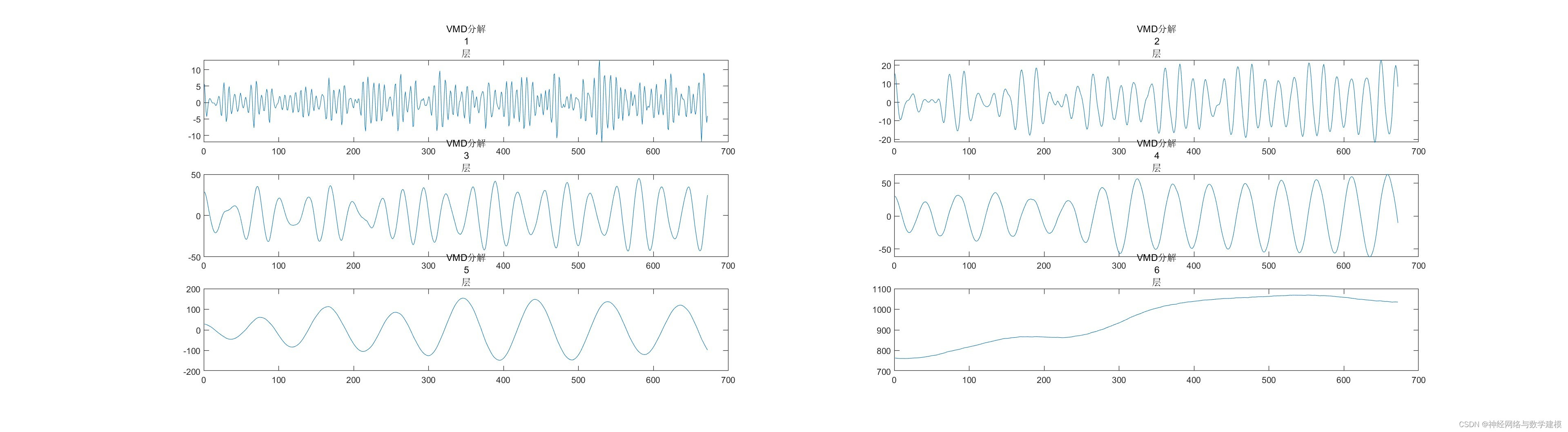
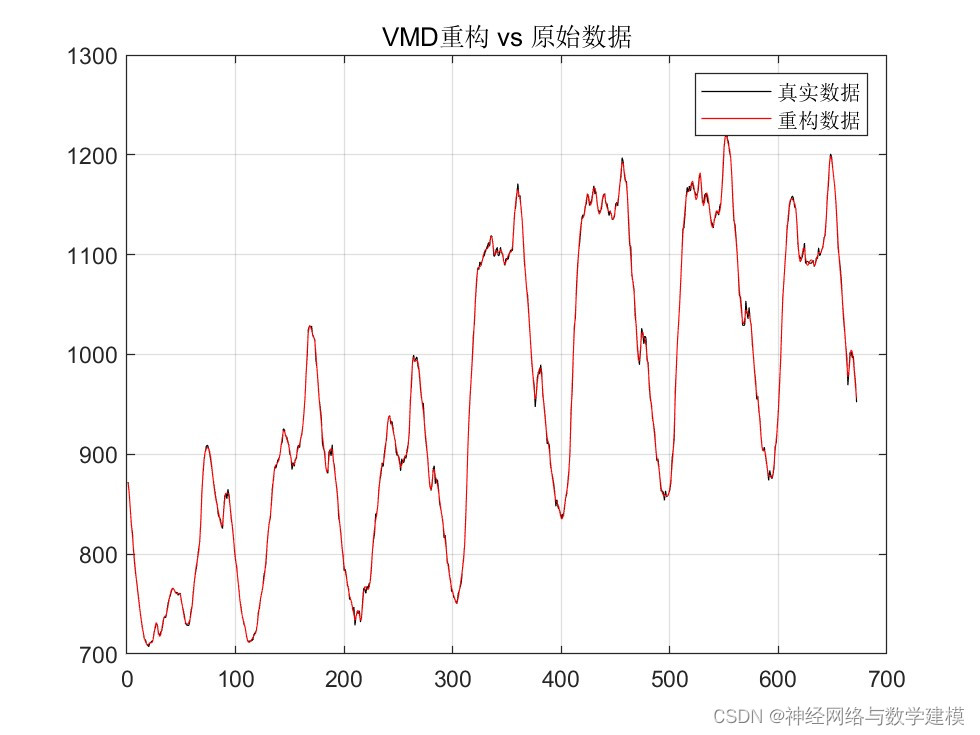
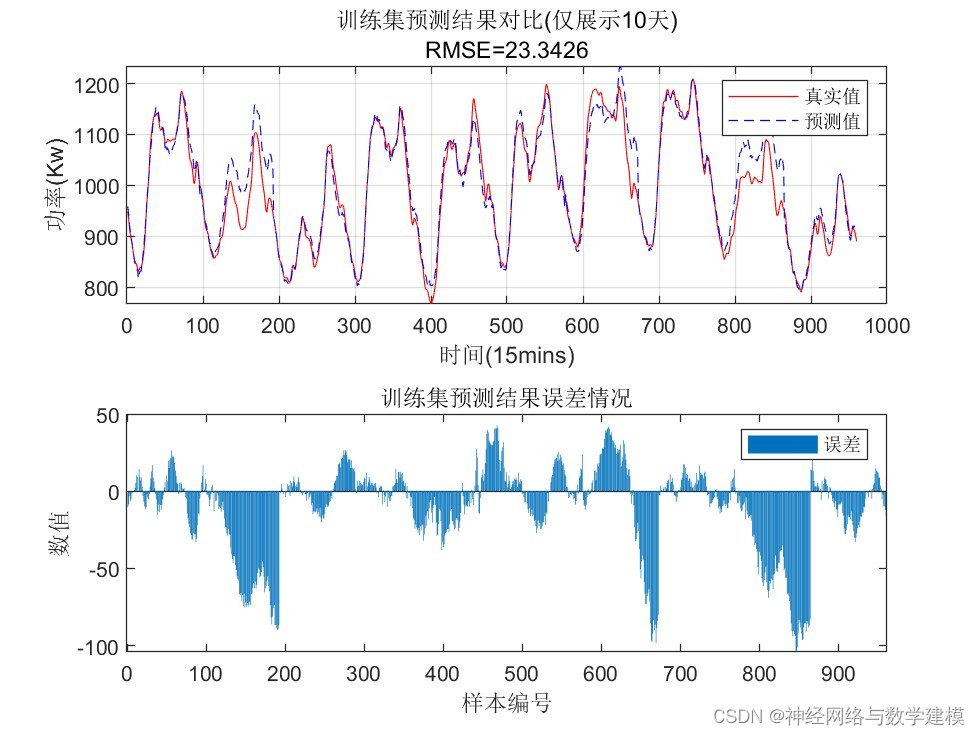
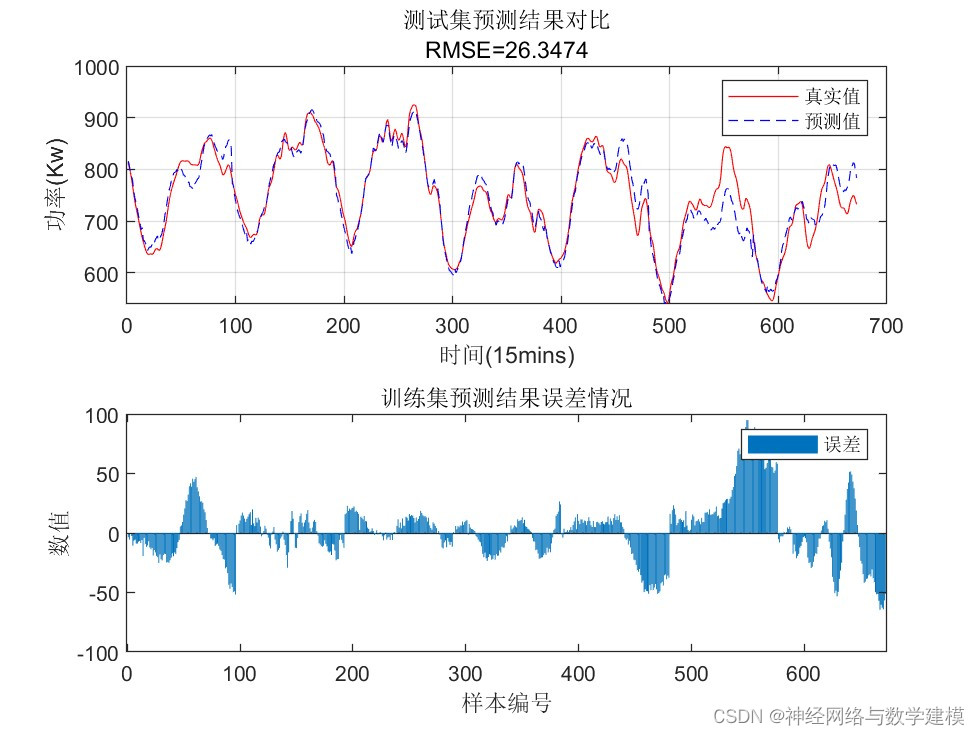
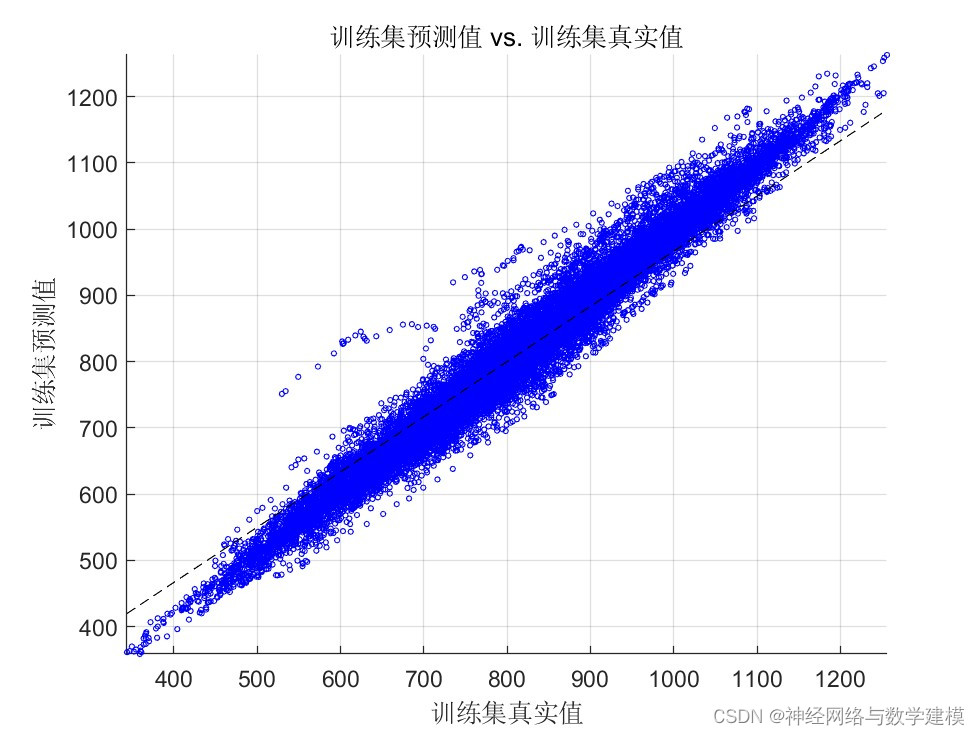
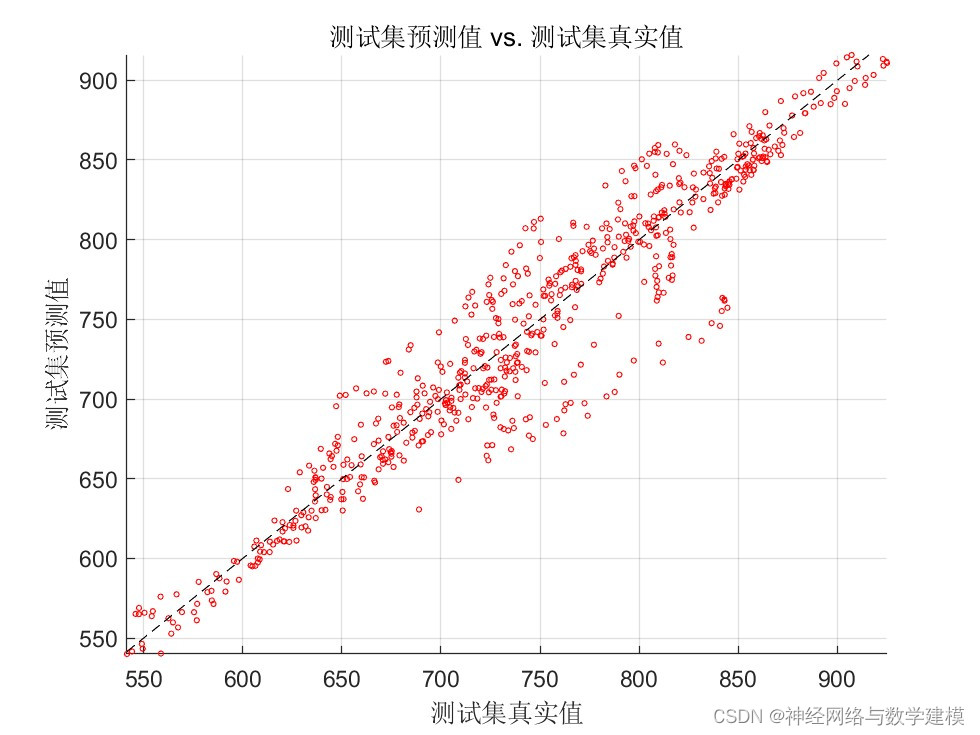
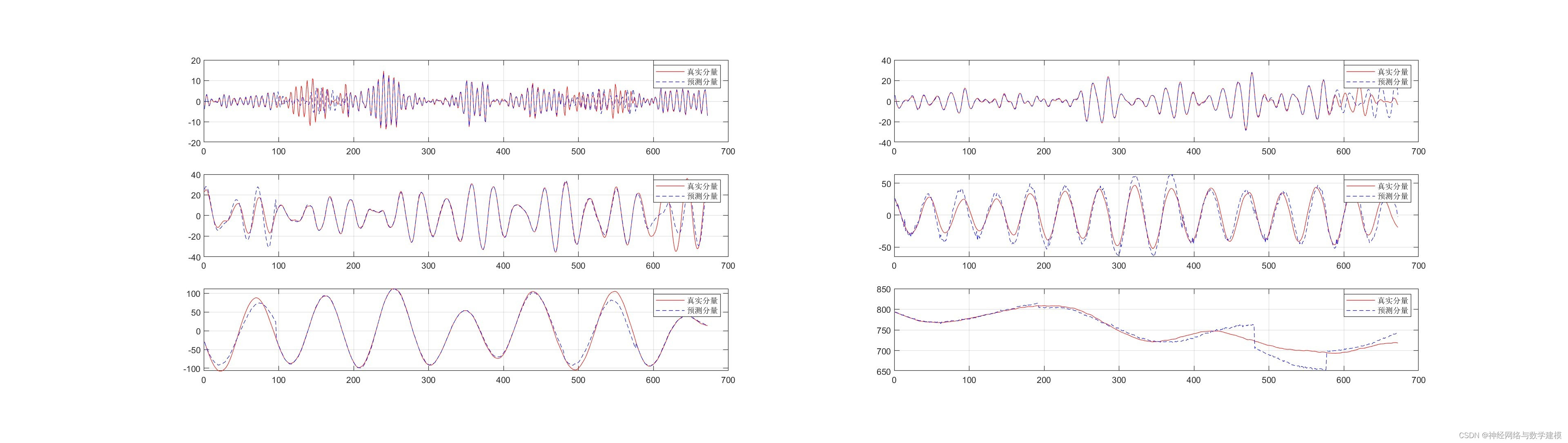
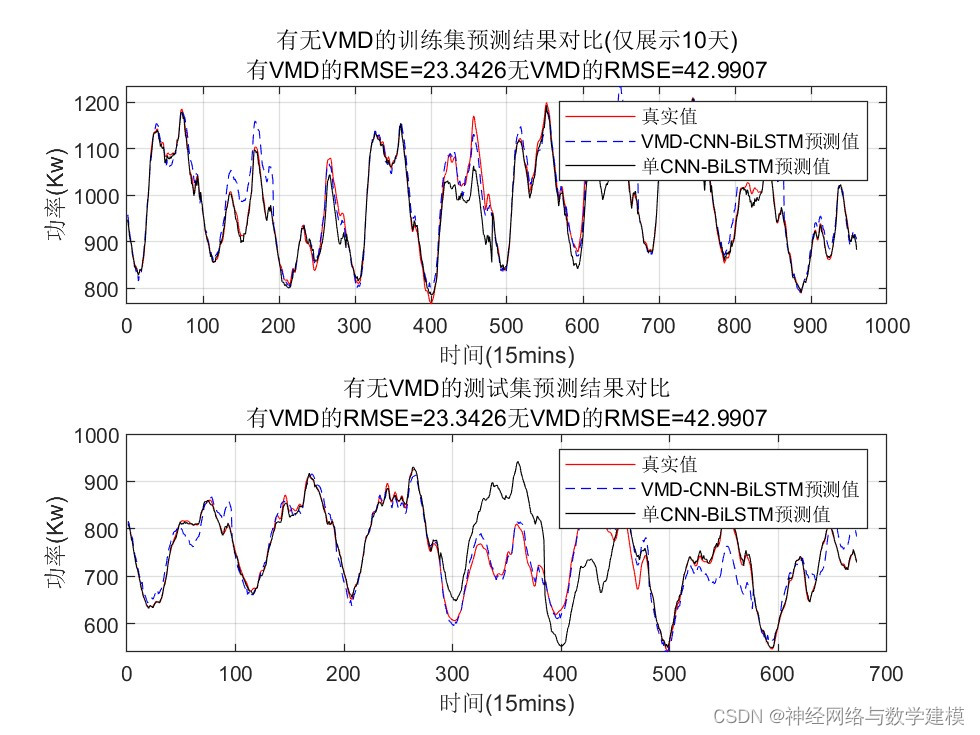
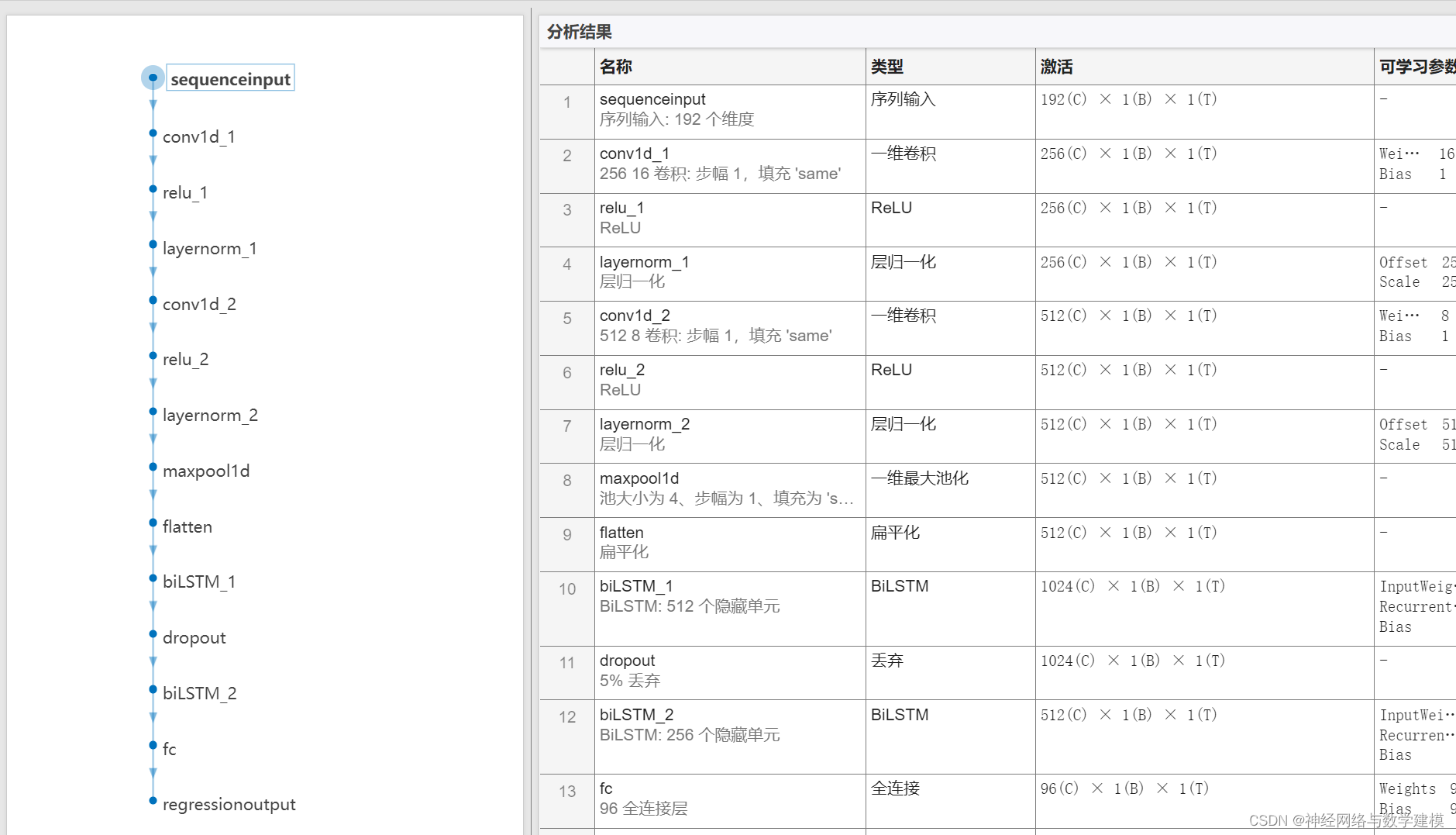
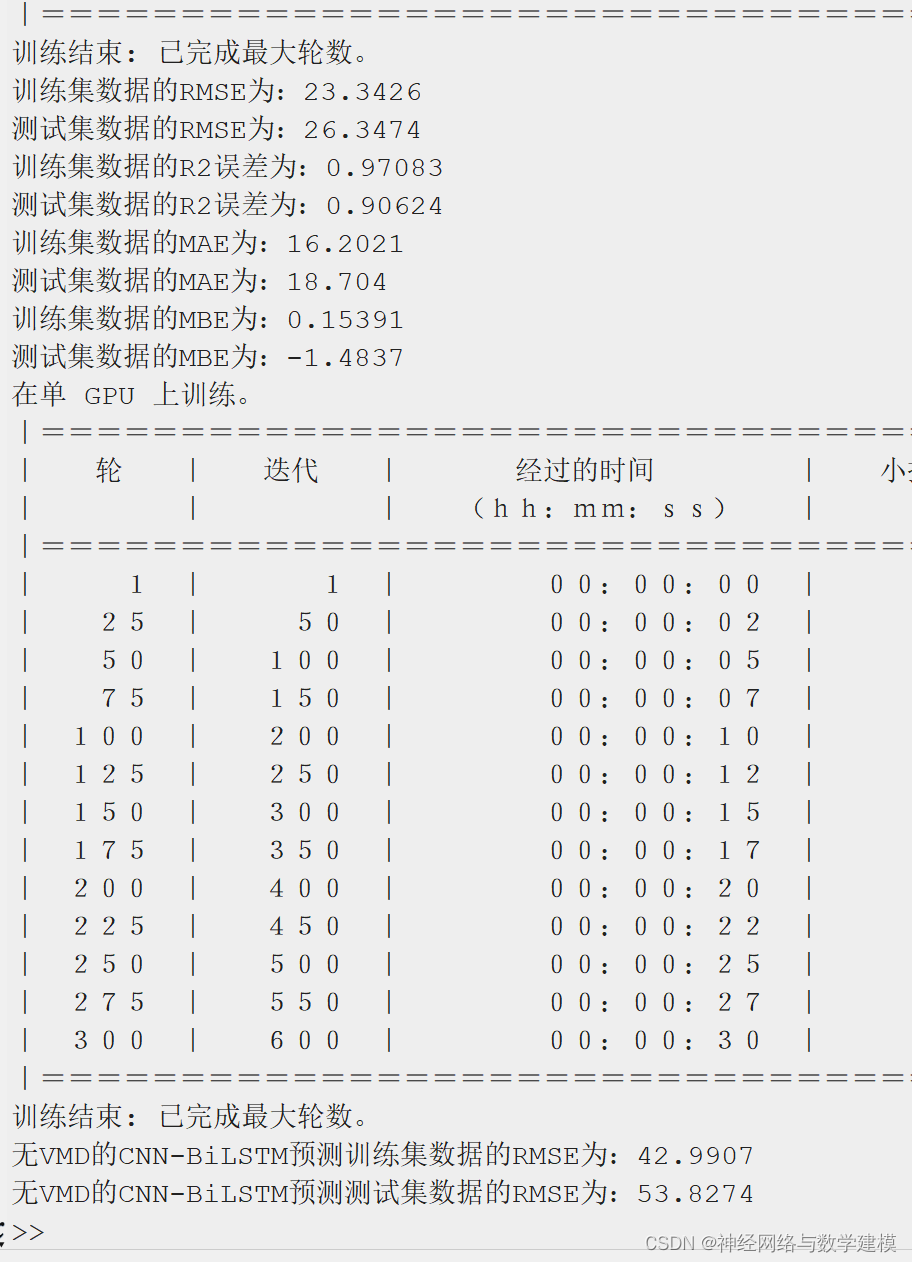
三、VMD-BiLSTM负荷预测理论:
为分离负荷数据中的信号和噪声,提高预测模型的精度,本文首先采用变分模态分解技术 将历史负荷数据分解成若干个本征模态分量,使其频率带宽之和最小化。然后利用深度学习神经网络CNN-BiLSTM分别对分解出的模态分量建模,CNN由于具有强大的特征筛选能力可以提取出信号中的关键特征信息,从而给后续网络提供更加精确的输入变量。BiLSTM神经网络由于具有记忆单元可以提取出更长的时间尺度上数据之间的关联性,在处理时间序列预测问题上能获得更高的精度。步骤如下:
(1)利用 VMD 技术将输入负荷分解成多个不同频率的本征模态分量
(2)对分解出的每个模态的负荷数据进行归一化处理。
(3)针对每个模态分量分别建立 CNN-BiLSTM 模型, 以当前时间之前48小时负荷序列为模型输入,预测未来24小时的负荷值。
(4)结合每个模型的输出,重构预测结果。
四、代码+数据下载:
相关文章:

(创新)基于VMD-CNN-BiLSTM的电力负荷预测—代码+数据
目录 一、主要内容: 二、运行效果: 三、VMD-BiLSTM负荷预测理论: 四、代码数据下载: 一、主要内容: 本代码结合变分模态分解( Variational Mode Decomposition,VMD) 和卷积神经网络(Convolutional neu…...

机器 reboot 后 kubelet 目录凭空消失的灾难恢复
文章目录 [toc]事故背景报错内容 修复过程停止 kubelet 服务备份 kubelet.config重新生成 kubelet.config重新生成 kubelet 配置文件对比 kubeadm-flags.env 事故背景 因为一些情况,需要 reboot 服务器,结果 reboot 机器后,kubeadm init 节点…...

Pytorch构建vgg16模型
VGG-16 1. 导入工具包 import torch.optim as optim import torch import torch.nn as nn import torch.utils.data import torchvision.transforms as transforms import torchvision.datasets as datasets from torch.utils.data import DataLoader import torch.optim.lr_…...
分支结构相关
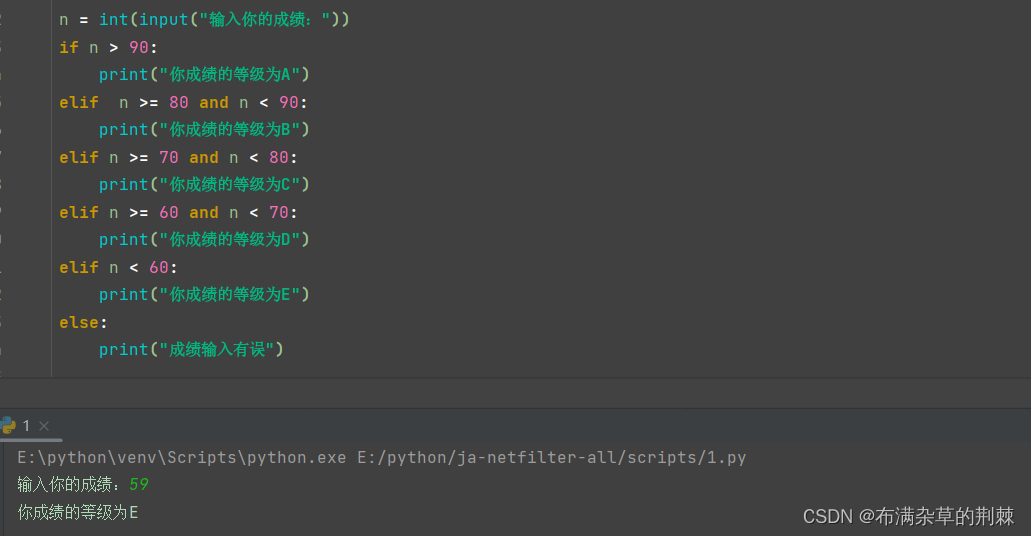
1.if 语句 结构: if 条件语句: 代码块 小练习: 使用random.randint()函数随机生成一个1~100之间的整数,判断是否是偶数 import random n random.randint(1,100) print(n) if n % 2 0:print(str(n) "是偶数") 2.else语…...

flutter开发实战-RichText富文本居中对齐
flutter开发实战-RichText富文本居中对齐 在开发过程中,经常会使用到RichText,当使用RichText时候,不同文本字体大小默认没有居中对齐。这里记录一下设置过程。 一、使用RichText 我这里使用RichText设置不同字体大小的文本 Container(de…...
智慧消防新篇章:可视化数据分析平台引领未来
一、什么是智慧消防可视化数据分析平台? 智慧消防可视化数据分析平台,运用大数据、云计算、物联网等先进技术,将消防信息以直观、易懂的图形化方式展示出来。它不仅能够实时监控消防设备的运行状态,还能对火灾风险进行预测和评估…...

u8g2 使用IIC驱动uc1617 lcd有时候某些像素显示不正确
折腾了很久,本来lcd是挂载到已经存在的iic总线上的,总线原来是工作正常的,挂载之后lcd也能显示,但是有时候显示不正确,有时候全白的时候有黑色的杂点。 解决方案: 1.最开始以为是IIC总线速度快࿰…...

使用opencv合并两个图像
本节的目的 linear blending(线性混合)使用**addWeighted()**来添加两个图像 原理 (其实我也没太懂,留个坑,感觉本科的时候线代没学好。不对,我本科就没学线代。) 源码分析 源码链接 #include "opencv2/imgc…...
k8s学习笔记(一)
configMap 一般用来存储配置信息 创建configMap 从文件中获取信息创建:kubectl create configmap my-config --from-file/tmp/k8s/user.txt 直接指定信息: kubectl create configmap my-config01 --from-literalkey1config1 --from-literalkey2confi…...

自学前端——JavaScript篇
JavaScript 什么是JavsScript JavaScript是一种轻量级、解释型、面向对象的脚本语言。它主要被设计用于在网页上实现动态效果,增加用户与网页的交互性。 作为一种客户端语言,JavaScript可以直接嵌入HTML,并在浏览器中执行。 与HTML和CSS不…...

高考毕业季--浅谈自己感想
随着2024年高考落幕,数百万高三学生又将面临人生中的重要抉择:选择大学专业。在这个关键节点,计算机相关专业是否仍是“万金油”的选择?在过去很长一段时间里,计算机科学与技术、人工智能、网络安全、软件工程等专业一…...
遥感图像地物覆盖分类,数据集制作-分类模型对比-分类保姆级教程
遥感图像地物覆盖分类,数据集制作-分类模型对比-分类保姆级教程 在遥感影像上人工制作分类数据集采用python+gdal库制作数据集挑选分类模型(RF、KNN、SVM、逻辑回归)选择随机森林模型建模分类遥感图像预测在遥感影像上人工制作分类数据集 1.新建shp文件 地理坐标系保持和影像…...

【Android面试八股文】Kotlin内置标准函数let的原理是什么?
确实,let 函数在 Kotlin 中被广泛使用,特别是在处理可空类型或者需要在对象上执行一系列操作后返回结果的场景中非常有用。 let 函数的源代码 /*** Calls the specified function [block] with `this` value as its argument and returns its result.** For detailed usage i…...

网工面试总结1
网工还是要基本会ACL、ISIS、OSPF、MPLS、QOS、GVRP、VRRP、FW、BGP、STP、IV4\6、WLAN、路由策略、策略路由、LACP等都或多或少要知道,常见的哪怕没有实战,要在ensp、cisco中练过! OSPF邻居故障,你认为是哪些原因?或者…...
[stm32]密码锁
[stm32]密码锁 需要资料的请在文章末尾获取~ 01描述 使用原件:stm32f103c8t6最小系统板x1,0.96寸OLED显示屏四角x1,4x4矩阵按键x1; 键位对应图: 1, 2, 3, 4------------- 1 2 3 4 5&am…...

优化yarn在任务执行时核数把控不准确的问题
核数不准这个事情是个概率问题,如果你碰见了,只能说你有点非欧,本质上是因为集群配置问题,默认时yarn不会去精准把控任务的核数,因为默认的资源计算方式是用实际内存去估算核数,这就导致如果大家配置任务时…...

2024年,收付通申请开通流程
大家好,今天咱们来聊聊关于APP场景中开通微信收付通的一些实用小窍门。在如今的移动互联网时代,很多商家都选择通过APP来提供服务和产品,因此如何在APP中顺利集成微信收付通功能,让用户能够轻松完成支付,就显得尤为重要…...

Django使用django-apscheduler实现定时任务
定时任务可以在后台定时执行指定的代码,避免了很多人为操作。下面是在Django项目中如何使用定时任务的具体操作流程。 我在这里使用的 django-apscheduler库来实现定时任务。 一、安装 django-apscheduler pip install django-apscheduler二、在项目的setting.py…...

python数据分析:修改数据
在 Python 中进行数据分析时,通常使用 pandas 库来处理和修改数据。以下是一个完整的示例,展示如何使用 pandas 库读取数据、修改数据并保存结果。 1. 安装并导入必要的库 首先,确保你已经安装了 pandas 库。如果没有安装,可以使…...

【免费API推荐】:解锁无限创意,让您的应用更具竞争力(8)
热门高效的免费实用类API是当今开发者们追逐的宝藏。这些API提供了各种热门功能和服务,能够帮助开发者轻松地为应用程序增添实用性和吸引力。无论是人脸识别、自然语言处理、机器学习还是图像处理,这些热门高效的免费API提供了强大的功能和高效的性能&am…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

前端开发者常用网站
Can I use网站:一个查询网页技术兼容性的网站 一个查询网页技术兼容性的网站Can I use:Can I use... Support tables for HTML5, CSS3, etc (查询浏览器对HTML5的支持情况) 权威网站:MDN JavaScript权威网站:JavaScript | MDN...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...

CentOS 7.9安装Nginx1.24.0时报 checking for LuaJIT 2.x ... not found
Nginx1.24编译时,报LuaJIT2.x错误, configuring additional modules adding module in /www/server/nginx/src/ngx_devel_kit ngx_devel_kit was configured adding module in /www/server/nginx/src/lua_nginx_module checking for LuaJIT 2.x ... not…...

Linux系统:进程间通信-匿名与命名管道
本节重点 匿名管道的概念与原理匿名管道的创建命名管道的概念与原理命名管道的创建两者的差异与联系命名管道实现EchoServer 一、管道 管道(Pipe)是一种进程间通信(IPC, Inter-Process Communication)机制,用于在不…...
