c++题目_水仙花数
水仙花数-普及-题目-ACGO题库
题目描述
求100-n中的水仙花数。一个数x,x的百位、十位、个位,分别用a、b、c来表示;
当a * a * a + b * b * b + c * c * c = x时,x就被称为水仙花数。(n<= 999)
输入格式
一行一个整数n
输出格式
每行一个整数
输入输出样例
-
输入#1
复制154
输出#1
复制153
代码:
#include<bits/stdc++.h>
using namespace std;
int main(){int n,a,b,c;cin>>n;for(int i=100;i<=n;i++){int d=i;a=d/100;b=d/10%10;c=d%10;if(a*a*a+b*b*b+c*c*c==i) cout<<i<<endl; }return 0;
}
相关文章:

c++题目_水仙花数
水仙花数-普及-题目-ACGO题库 题目描述 求100-n中的水仙花数。一个数x,x的百位、十位、个位,分别用a、b、c来表示; 当a * a * a b * b * b c * c * c x时,x就被称为水仙花数。(n< 999) 输入格式 一行一个整数n 输出格式…...

使用 Iceberg、Tabular 和 MinIO 构建现代数据架构
现代数据环境需要一种新型的基础架构,即无缝集成结构化和非结构化数据、轻松扩展并支持高效的 AI/ML 工作负载的基础架构。这就是现代数据湖的用武之地,它为您的所有数据需求提供了一个中心枢纽。然而,构建和管理有效的数据湖可能很复杂。 这…...

jnp.linalg.norm
jnp.linalg.norm 是 JAX 中用于计算向量或矩阵的范数的函数。JAX 是一个用于高性能机器学习研究的 Python 库,它提供了与 NumPy 类似的 API,但支持自动微分和加速计算。jnp 是 JAX 的 NumPy 接口。 jnp.linalg.norm 的基本语法 jnp.linalg.norm(x, ord…...
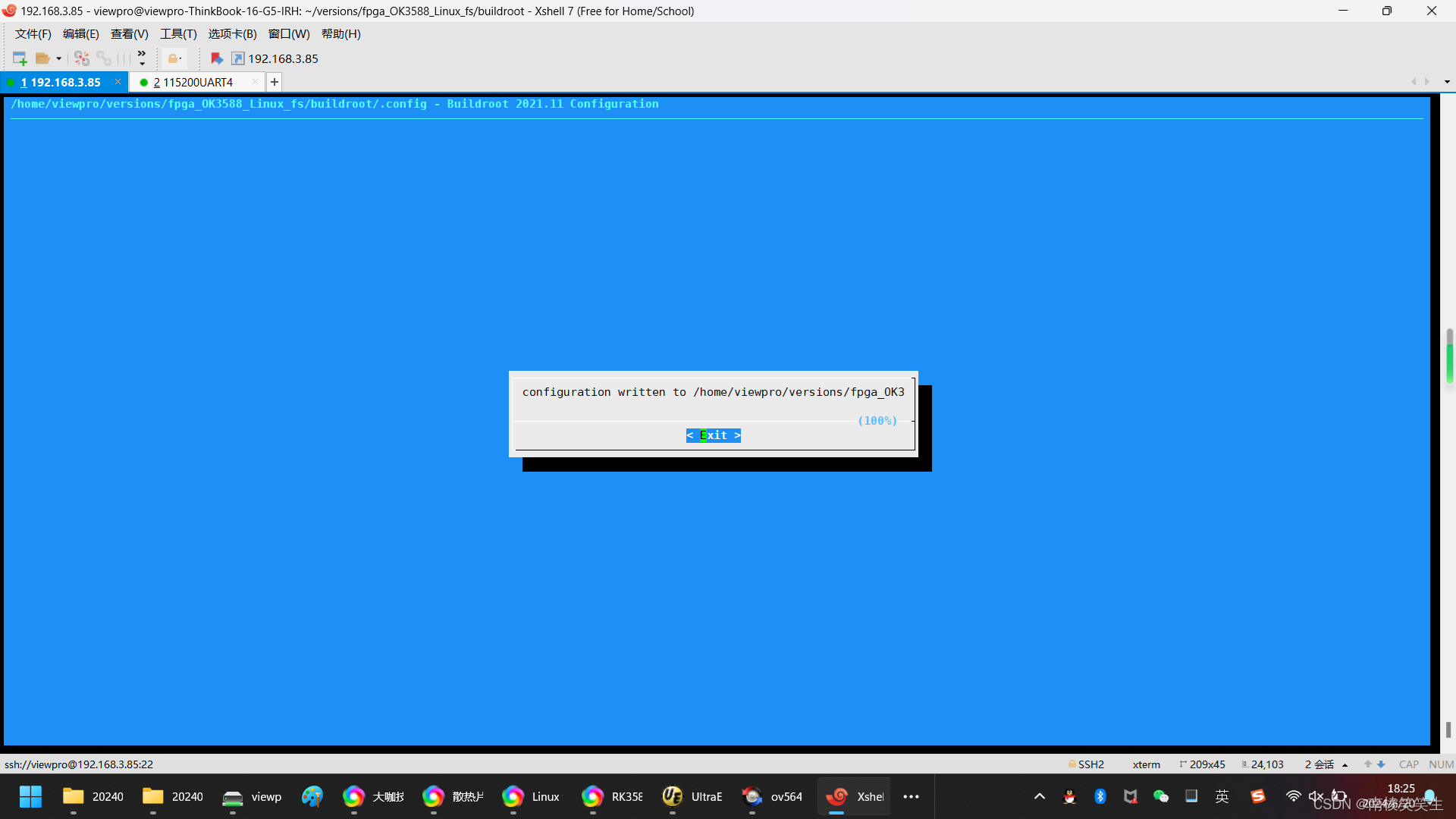
20240621在飞凌的OK3588-C开发板的Buildroot系统中集成i2ctool工具
20240621在飞凌的OK3588-C开发板中打开i2ctool工具 2024/6/21 17:44 默认继承的i2c工具: rootrk3588-buildroot:/# rootrk3588-buildroot:/# i2c i2c-stub-from-dump i2cdump i2cset i2cdetect i2cget i2ctransfer rootrk3588-…...

ARM32开发--存储器介绍
知不足而奋进 望远山而前行 目录 文章目录 前言 存储器分类 RAM ROM EEPROM Flash 总结 前言 在现代计算机系统中,存储器扮演着至关重要的角色,不仅影响着数据的存取速度和稳定性,还直接关系到计算机系统的性能和应用场景的选择。存…...

Web服务器
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 当在浏览器输入URL后,浏览器会先请求DNS服务器,获得请求站点的 IP 地址(即根据URL地址“www.mingrisoft.com”获取…...

大语言模型-Transformer
目录 1.概述 2.作用 3.诞生背景 4.历史版本 5.优缺点 5.1.优点 5.2.缺点 6.如何使用 7.应用场景 7.1.十大应用场景 7.2.聊天机器人 8.Python示例 9.总结 1.概述 大语言模型-Transformer是一种基于自注意力机制(self-attention)的深度学习…...

POI:接收上传上来的excel,解析并导入到数据库
目录 1、控制层 2、业务层(主要逻辑) 1、控制层 因为前端设置了只能上传1个文件,这里直接取一个。 RequestMapping(value "/shebeiDaoru.ctrl", method RequestMethod.POST, produces "application/json;charsetUTF-8&q…...

网页的CSS和JavaScript文件没有自动更新, 解决办法
项目场景: 无人值守的场馆预定以及管理 问题描述 更新了CSS和JavaScript,访问始终样式不对 原因分析: 浏览器缓存了你的CSS和JavaScript文件 浏览器缓存了你的CSS和JavaScript文件。当文件的修改时间戳(last-modifiedÿ…...

Go语言 获取服务器资源磁盘Disk情况
1、获取整个磁盘的总量、已使用量、使用率 package mainimport ("fmt""github.com/shirou/gopsutil/disk""log" )func main() {// 获取所有挂载点的磁盘使用率信息partitions, err : disk.Partitions(false)if err ! nil {log.Fatalf("Err…...

使用上海云盾 CDN 和 CloudFlare 后 Nginx、 WordPress、 Typecho 获取访客真实 IP 方法
最近因为被 DDoS/CC 攻击的厉害,明月就临时的迁移了服务器,原来的服务器就空置下来了,让明月有时间对服务器进行了重置重新部署安装生产环境。因为站点同时使用了上海云盾和 CloudFlare(具体思路可以参考【国内网站使用国外 CloudFlare CDN 的思路分享】一文)两个 CDN 服务…...

深入探究RTOS的任务调度
阅读引言: 此文将会从一个工程文件, 一步一步的分析RTOS的任务调度实现, 这里选用FreeRTOS分析, 别的也差不多的, 可能在细节上有少许不一样。 目录 1, 常见嵌入式实时操作系统 2, 任务调度的…...

【shell脚本速成】函数
文章目录 一、函数1.1、函数介绍1.2、函数定义1.3、函数调用 🌈你好呀!我是 山顶风景独好 🎈欢迎踏入我的博客世界,能与您在此邂逅,真是缘分使然!😊 🌸愿您在此停留的每一刻…...
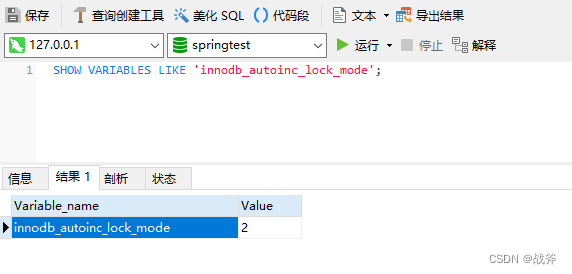
拒绝零散碎片, 一文理清MySQL的各种锁
系列文章目录 学习MySQL先有全局观,细说其发展历程及特点 Mysql常用操作,谈谈排序与分页 拒绝零散碎片, 一文理清MySQL的各种锁(收藏向) 系列文章目录一、MySQL的锁指什么二、排他与共享三、全局锁(Global…...

P5711 【深基3.例3】闰年判断
1. 题目链接 https://www.luogu.com.cn/problem/P5711 P5711 【深基3.例3】闰年判断 2. 题目描述 题目描述:判断一个数是否是闰年 输入:输入一个整数n 输出:输出1或0,如果是闰年,输出1,否则输出0 3. 我的…...

基于Raft算法实现的分布式键值对存储系统——学习笔记
目录 1 基于Raft算法实现的分布式键值对存储系统 1.1 模块 2 Raft 算法 2 .1 概念 2.2 raft角色(先简单了解,方便后续阅读) 2.3 raft想解决什么问题? 2.4 选举领导 2.5 领导者故障 附录: 参考文献࿱…...
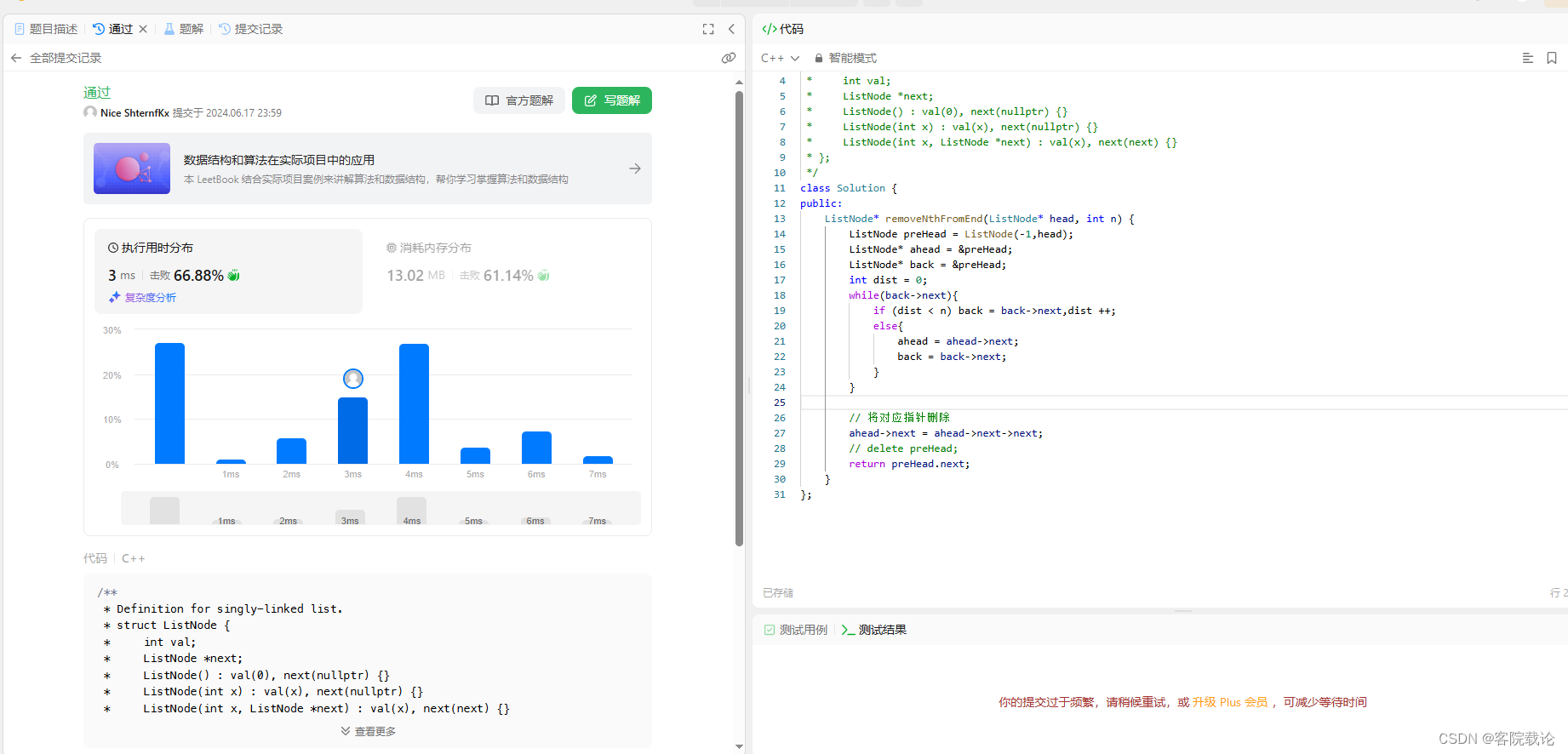
秋招突击——6/17——复习{整理昨天的面试资料}——新作{删除链表倒数第n个节点}
文章目录 引言复习新作删除链表倒数第N个节点题目描述个人实现参考实现 总结 引言 主管面,面的很凄惨,不过无所谓了,我已经尽力了。上午都在整理的面经,没有复习算法,而且这两天要弄一下论文,二十号就要提…...
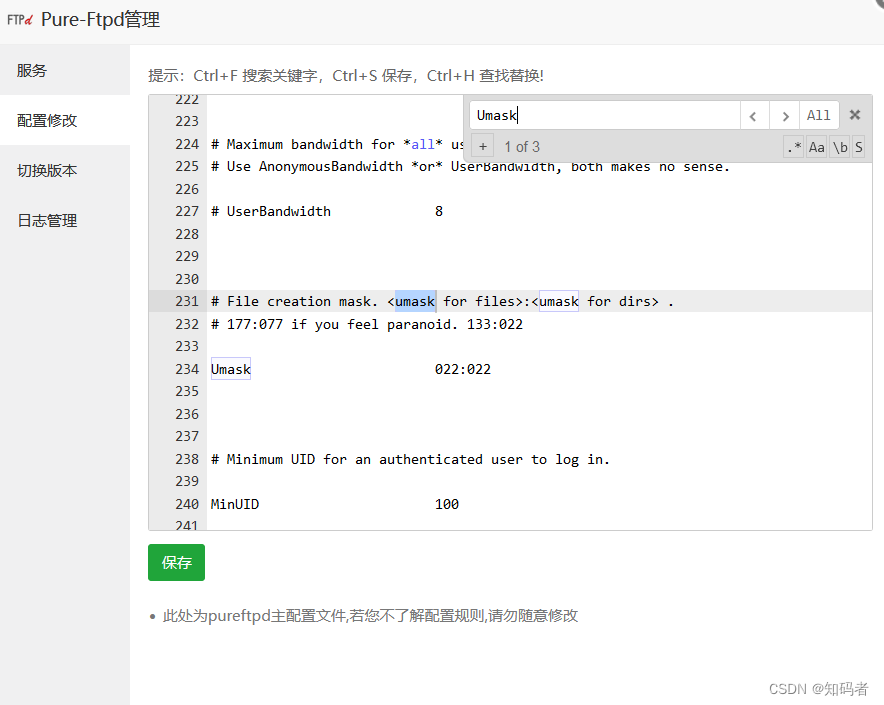
宝塔面板使用技巧(pure-FTP)上传文件和文件夹默认权限644的修改
前言 科技在进步各种各样的开源软件和库让我们应接不暇,我估计现在所有做php开发的人员都知道宝塔面板,我就经常用,但是不知道大家出现过一个问题不就是在我们开发过程中需要实时的给服务器上传我们开发的文件那么就涉及到了宝塔自带的pure-F…...

mac m芯片安装win11遇坑
mac m芯片安装win11遇坑 1、下载arm架构镜像 磁力链接: magnet:?xturn:btih:e8c15208116083660709eac9aee124e025c01447&dnSW_DVD9_Win_Pro_11_22H2_64ARM_ChnSimp_Pro_Ent_EDU_N_MLF_X23-12755.ISO&xl57198960642、使用VMWare Fusion安装,启…...
一个自定义流程的平台
脚本语言使用的是C#,当用户发布一个新的流程时,会把C#的脚本编译成dll,然后添加到微服务中,因为有了硬编译,所以执行速度是非常快的。逻辑脚本支持调试,可以断点和逐行调试。平台提供了调试工具,…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
