Python设计模式 - 简单工厂模式
定义
简单工厂模式是一种创建型设计模式,它通过一个工厂类来创建对象,而不是通过客户端直接实例化对象。
结构
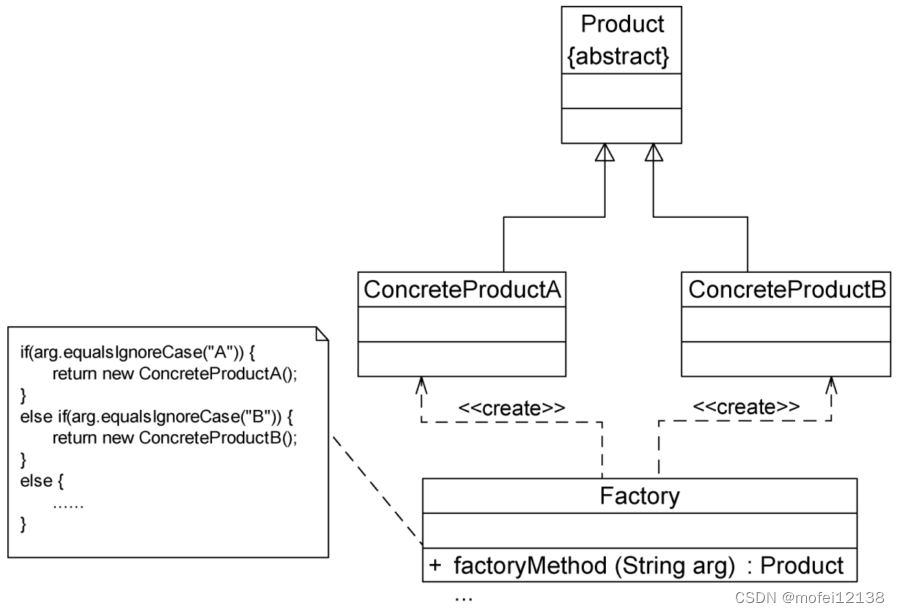
工厂类(Factory):负责创建对象的实例。工厂类通常包含一个方法,根据输入参数的不同创建并返回不同的对象。
产品类(Product):工厂类创建的对象接口或抽象类,所有具体产品类需要实现或继承这个接口或抽象类。
具体产品类(ConcreteProduct):实现了产品接口的具体类。
应用场景
- 多种产品对象的创建:当系统需要创建多种类型的对象(不宜过多),而且这些对象有着相似的结构或接口时,可以使用简单工厂模式来集中管理对象的创建逻辑。这有助于提高代码的可维护性和扩展性。例如,不同类型的图形对象、不同类型的报表生成器等。
- 避免直接实例化复杂对象:当对象的创建过程较为复杂,涉及多种初始化步骤时,可以使用简单工厂模式,将这些初始化步骤封装在工厂类中,简化客户端代码。例如,不同类型的数据库连接、复杂的对象初始化流程等。
优缺点
优点:
- 简化客户端代码:客户端代码不需要了解具体产品类的创建细节,只需调用工厂类的创建方法即可获得所需的对象。这减少了客户端代码的复杂性,使其更容易维护和理解。
- 集中管理对象的创建:对象的创建逻辑集中在工厂类中,便于统一管理和控制。这有助于在一个地方进行修改和调整,从而避免在多个地方重复修改代码,提高了代码的可维护性。
- 便于扩展:当需要增加新产品类时,只需在工厂类中添加相应的创建逻辑,客户端代码无需修改。这使得系统在一定程度上具有较好的扩展性。
缺点:
- 违背开闭原则:每当需要添加新的产品类型时,都必须修改工厂类以添加新的创建逻辑。这违反了开闭原则,增加了维护成本。
- 违背单一职责原则:工厂类不仅负责创建对象,还承担了对象的选择逻辑,可能会导致工厂类变得复杂,难以维护。
- 不可避免的条件判断:工厂类中通常会包含大量的条件判断语句(如if-else或switch-case),用于确定需要创建哪种类型的对象。这些条件判断语句会随着产品种类的增加而变得冗长且复杂。
代码示例
from abc import ABC, abstractmethodclass Shape(ABC):@abstractmethoddef draw(self):passclass Circle(Shape):def draw(self):return "Drawing a Circle"class Rectangle(Shape):def draw(self):return "Drawing a Rectangle"class ShapeFactory:@staticmethoddef create_shape(shape_type):if shape_type == "CIRCLE":return Circle()elif shape_type == "RECTANGLE":return Rectangle()else:raise ValueError("Unknown shape type")if __name__ == "__main__":# 使用工厂类创建对象shape = ShapeFactory.create_shape("CIRCLE")print(shape.draw()) # 输出: Drawing a Circleshape = ShapeFactory.create_shape("RECTANGLE")print(shape.draw()) # 输出: Drawing a Rectangle
参考
《设计模式的艺术》
相关文章:

Python设计模式 - 简单工厂模式
定义 简单工厂模式是一种创建型设计模式,它通过一个工厂类来创建对象,而不是通过客户端直接实例化对象。 结构 工厂类(Factory):负责创建对象的实例。工厂类通常包含一个方法,根据输入参数的不同创建并返…...

L55--- 257.二叉树的所有路径(深搜)---Java版
1.题目描述 2.思路 (1)因为是求二叉树的所有路径 (2)然后是带固定格式的 所以我们要把每个节点的整数数值换成字符串数值 (3)首先先考虑根节点,也就是要满足节点不为空 返回递归的形式dfs(根节…...

智慧园区解决方案PPT(53页)
## 1.1 智慧园区背景及需求分析 - 智慧园区的发展历程包括园区规划、经济、产业、企业、管理、理念的转变,强调管理模式创新,关注业务综合化、管理智慧化等发展。 ## 1.2 国家对智慧园区发展的政策 - 涉及多个国家部门,如工信部、住建部、…...
)
Windows安装MySQL(8.0.37)
安装:https://blog.csdn.net/XLBYYDS/article/details/139711682 注意点: (1)必须安装到C盘系统盘,否则执行 net start mysql 启动服务时,可能会启动失败。 (2)如果安装时出现 The…...
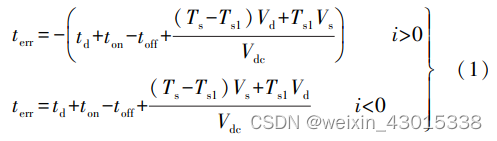
永磁同步电机驱动死区补偿
1 死区效应及补偿 1. 1 死区效应 在本文的电机控制嵌入式系统中,逆变器为三 相电压型桥式逆变电路,如图 1 所示。 在理想状态 下,上桥臂和下桥臂的控制信号满足互补通断原则, 即上桥臂开通时,下桥臂关断,反之亦然。 而在实际 应用中,开关管的通断需要一定的开通时…...

智能体合集
海外版coze: 前端代码助手 后端代码助手: 前端代码助手:...

智能农业管理系统设计
一、引言 随着物联网、云计算和大数据技术的快速发展,智能农业管理系统成为提高农业生产效率、优化资源配置、降低环境污染的重要手段。本设计旨在构建一个集数据采集、传输、处理、分析于一体的智能农业管理系统,为农业生产提供全方位、精准化的服务。 …...
Matlab的Simulink系统仿真(simulink调用m函数)
这几天要用Simulink做一个小东西,所以在网上现学现卖,加油! 起初的入门是看这篇文章MATLAB 之 Simulink 操作基础和系统仿真模型的建立_matlab仿真模型搭建-CSDN博客 写的很不错 后面我想在simulink中调用m文件 在 Simulink 中调用 MATLA…...

C语言中操作符详解(一)
众所周知,在我们的C语言中有着各式各样的操作符,并且在此之前呢,我们已经认识并运用了许许多多的操作符,都是诸君的老朋友了昂 操作符作为我们使用C语言的一个非常非常非常重要的工具,诸君一定要加以重视,…...

【论文阅读】Multi-Camera Unified Pre-Training via 3D Scene Reconstruction
论文链接 代码链接 多摄像头三维感知已成为自动驾驶领域的一个重要研究领域,为基于激光雷达的解决方案提供了一种可行且具有成本效益的替代方案。具有成本效益的解决方案。现有的多摄像头算法主要依赖于单目 2D 预训练。然而,单目 2D 预训练忽略了多摄像…...

深入了解NumPy的原理与使用
文章目录 一、引言二、NumPy的原理1. 多维数组对象2. 广播(Broadcasting)3. 内存效率和速度 三、NumPy的使用1. 创建数组2. 数组操作3. 广播(Broadcasting)示例 四、总结 一、引言 在Python的数据科学和科学计算领域,…...

Linux Centos 环境下搭建RocketMq集群(双主双从)
1、下载rocketmq的包 下载 | RocketMQ 2、配置环境变量 1、编辑环境变量文件:vim /etc/profile2、加入如下配置: #rocketmq 4.9.8 ROCKETMQ_HOME/home/rocketmq/rocketmq-4.9.8 export PATH${ROCKETMQ_HOME}/bin:${PATH}3、刷新配置:source…...

全网最全postman接口测试教程和项目实战~从入门到精通
Postman实现接口测试内容大纲一览: 一、什么是接口?为什么需要接口? 接口指的是实体或者软件提供给外界的一种服务。 因为接口能使我们的实体或者软件的内部数据能够被外部进行修改。从而使得内部和外部实现数据交互。所以需要接口。 比如&…...

【ARM】MDK Debug模式下Disassembly窗口介绍
【更多软件使用问题请点击亿道电子官方网站】 1、 文档目标 主要了解Disassembly窗口中包含的内容,和如何利用Disassembly中的内容了解程序的存储和调用情况。 2、 问题场景 对于Disassembly窗口中具体包含的内容不了解,无法合理地应用Disassembly窗口…...

灵活的招聘管理系统有五种方法帮助成功招聘
还记得以前的时代吗?这取决于你的年龄,直到智能手机、流媒体电视和电子邮件出现。今天,任何活着的成年人都经历了技术上的巨大变化,这创造了一种新的行为方式。人才获取也是如此。 一个值得推荐的招聘管理系统 招聘团队被困在满足…...

美摄科技匿名化处理解决方案,包含模糊、同色、马赛克、效果遮挡等各种形式
信息安全已成为企业发展中不可忽视的重要一环,随着信息安全法规的日益严格和公众对个人隐私保护意识的不断提高,企业如何在保障业务顺畅进行的同时,满足信息安全和隐私保护的要求,成为了亟待解决的问题。美摄科技凭借其强大的技术…...

O2OA的数据库数据库配置-使用不同用户访问Oracle时报错-表或视图不存在
在使用Oracle数据库时,多个O2OA服务器同一个Oracle实例中使用不同的用户启动时,可能会遇到数据库访问的错误。本篇阐述此类问题以及解决方案。 一、先决条件: 1、O2OA已经下载并且解压到指定的目录; 2、Oracle数据库已经完成安…...

leetcode56 合并区间
题目 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 示例 输入:intervals [[1,3],[2,6]…...

Elasticsearch扩展性探索:水平扩展与集群管理
在当今数据驱动的时代,搜索引擎和数据存储解决方案的重要性不言而喻。Elasticsearch,作为一款基于Lucene构建的开源、分布式、RESTful搜索引擎,凭借其强大的全文搜索、结构化搜索和分析能力,受到了众多企业和开发者的青睐。然而&a…...

node版本过高出现ERR_OSSL_EVP_UNSUPPORTED错误
错误原因: 新版本的nodejs使用的openssl和旧版本不同,导致出错 解决方法: 1.将node版本重新换回16.x 2 windows 下 在package.json文件下添加set NODE_OPTIONS--openssl-legacy-provider && "scripts": {"dev"…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...
