数据结构6---树
一、定义
树(Tree)是n(n>=0)个结点的有限集。当n=0时成为空树,在任意一棵非空树中:
1、有且仅有一个特定的称为根(Root)的结点;
2、当n>1时,其余结点可分为m(m>日)个互不相交的有限集T1、T2、...、 Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
需要注意的是:
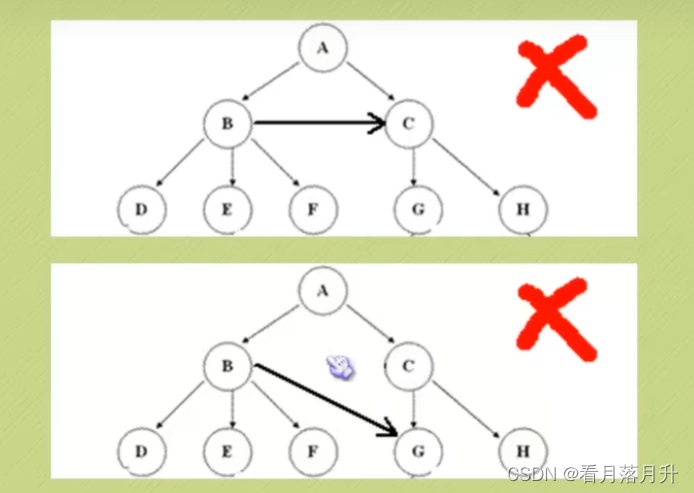
1、n>6时,根结点是唯一的,坚决不可能存在多个根结点。
2、m>0时,子树的个数是没有限制的,但它们互相是一定不会相交的。
二、节点分类
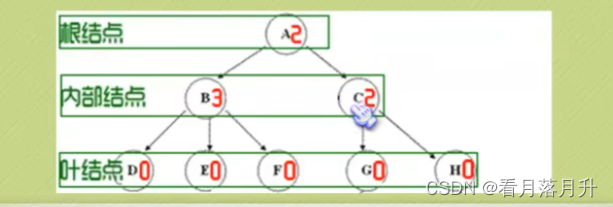
刚才所有图片中,每一个圈圈我们就称为树的一个结点。结点拥有的子树数称为结点的度-
(Degree),树的度取树内各结点的度的最大值。
1、度为0的结点称为叶结点(Leaf)或终端结点;
2、度不为0的结点称为分支结点或非终端结点,除根结点外,分支结点也称为内部结点。
三、结点间的关系
结点的子树的根称为结点的孩子(Child),相应的,该结点称为孩子的双亲(Parent),同一双亲的孩子之间互称为兄弟(Sibling)。
结点的祖先是从根到该结点所经分支上的所有结点。
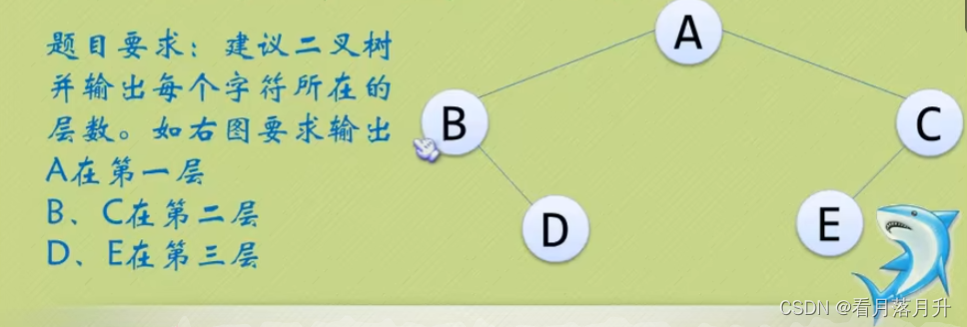
四、节点的层次
- 结点的层次(Level)从根开始定一起,根为第一层,根的孩子为第二层。
- 其双亲在同一层的结点互为堂兄弟。
- 树中结点的最大层次称为树的深度(Depth)或高度。
五、其他概念
- 如果将树中结点的各子树看成从左至右是有次序的,不能互换的,则称该树为有序树,否则称为无序树。
- 森林(Forest)是 m(m>=0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。
六、树的存储结构
1、双亲表示法
双亲表示法,言外之意就是以双亲作为索引的关键词的一种存储方式。
我们假设以一组连续空间存储树的结点,同时在每个结点中,附设一个指示其双亲结点在数组中位置的元素。
也就是说,每个结点除了知道自己是谁之外,还知道它的粑粑妈妈在哪里。
定义一个结构体
#define MAXSIZE 100typedef struct PTNode {int data; //结点数据int parent; //双亲位置
}PTNode;typedef struct {PTNode node[MAXSIZE];int r; //根的位置int n; //节点数目
}PTree;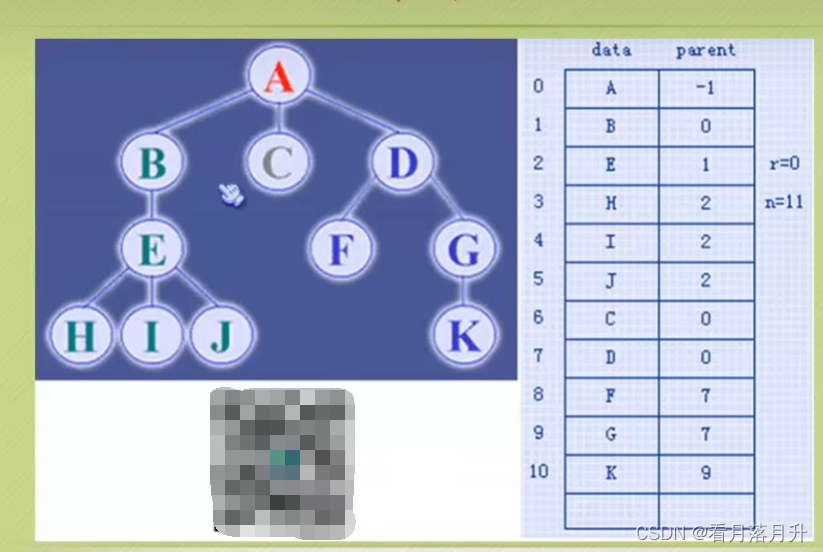
这样的存储结构,我们可以根据某结点的parent指针找到它的双亲结点,所用的时间复杂度是0(1),索引到parent的值为-1时,表示找到了树结点的根。
可是,如果我们要知道某结点的孩子是什么?那么不好意思,请遍历整个树结构
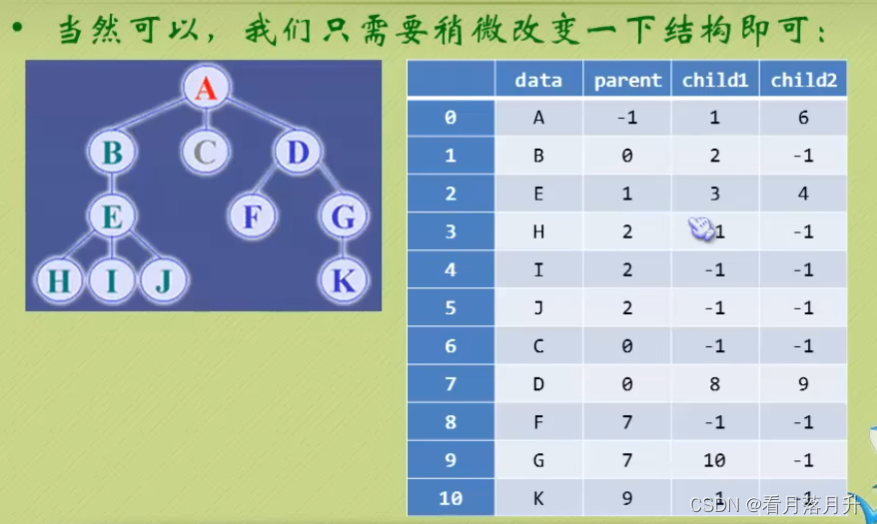
2、孩子表示法
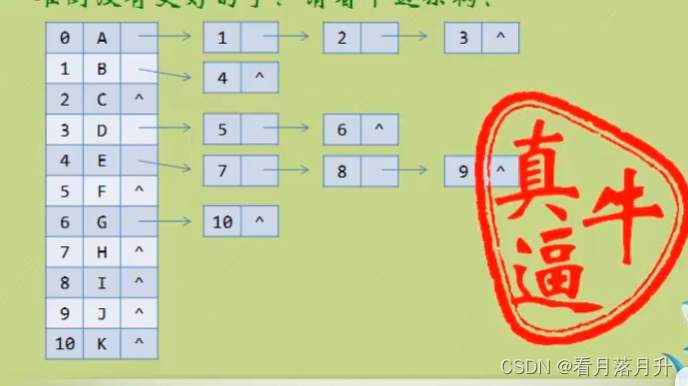
3、双亲孩子表示法
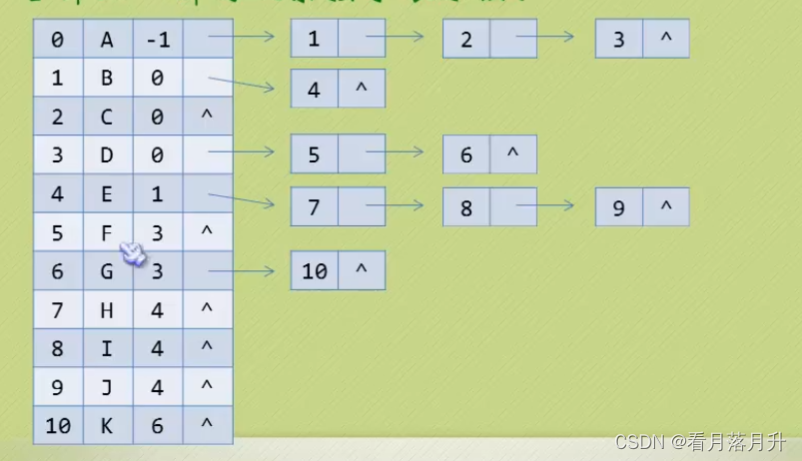
//孩子节点
typedef struct CTNode {int child; //孩子结点的下标struct CTNode* next; //指向下一个孩子结点的指针
}*ChildPtr;//表头结构
typedef struct {int data; //存放在树中的节点数据int paraent; //存放双亲的下标ChildPtr friendchild; //指向第一个孩子的指针
}CTBox;//树结构
typedef struct {CTBox node[MAXSIZE];int r, n;
}CTTree;七、二叉树
1、定义
二叉树(Binary Tree)是n(n>=0)个结点的有限集合,该集合或者为空集(空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
注意:
每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点。(注意:不是都需要两棵子树,而是最多可以是两棵,没有子树或者有一棵子树也都是可以的。)
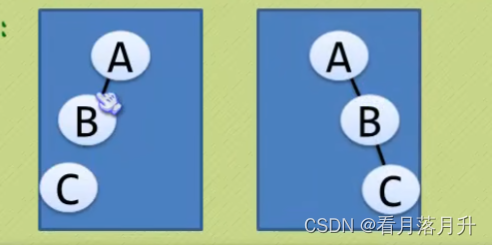
左子树和右子树是有顺序的,次序不能颠倒。
即使树中某结点只有一棵子树,也要区分它是左子树还是右子树,下面是完全不同的二叉树:
2、五种基本形态
(1)空二叉树
(2)只有一个根结点
(3)根结点只有左子树
(4)根结点只有右子树
(5)根结点既有左子树又有右子树
3、特殊二叉树
(1)斜树
斜树是一定要斜的,但斜也要斜寻有范儿
(2)满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
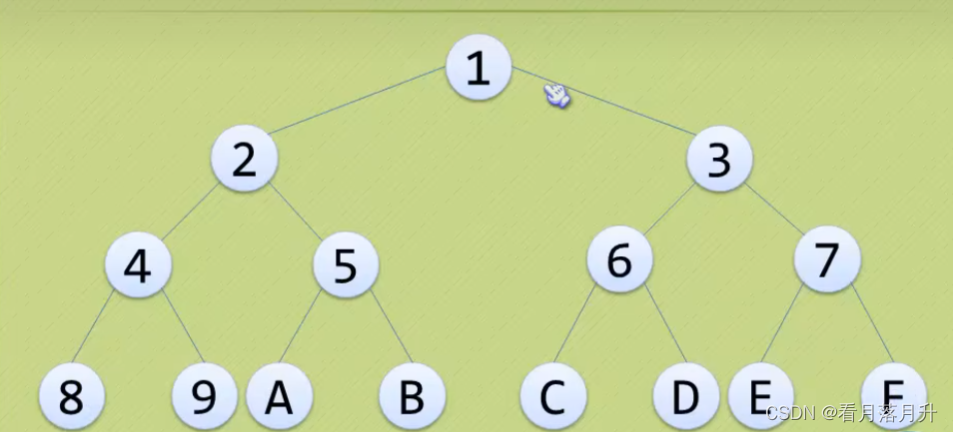
特点:
- 叶子只能出现在最下一层。
- 非叶子结点的度一定是2。
- 在同样深度的二叉树中,满二又树的结点个数一定最多,同时叶子也是最多。
(3)完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点位置完全相同,则这棵二叉树称为完全二叉树。
这个也是满二叉树
特点:
- 叶子结点只能出现在最下两层。
- 最下层的叶子一定集中在左部连续位置。
- 倒数第二层,若有叶子结点,一定都在右部连续位置。
- 如果结点度为1,则该结点只有左孩子。
- 同样结点树的二叉树,完全二叉树的深度最小。
注意:满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树。
重点:
二叉树的性质一:在二叉树的第i层上至多2^(i-1)个结点(i>=1)
二叉树的性质二:深度为k的二叉树至多有2^k-1个结点(k>=1)
二叉树的性质三:对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1

(打岔一下,在纸面上写写画画很重要的!!!)
二叉树的性质四:具有n个结点的完全二叉树的深度为 ,向下取整
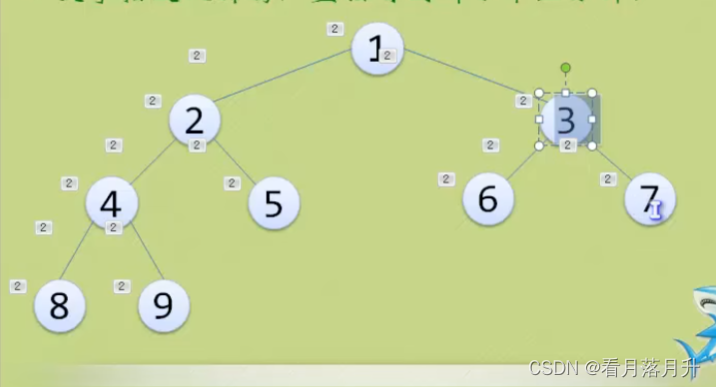
二叉树的性质五:如果对一棵有n个结点的完全二叉树(其深度为[log2n]+1)的结点按层序编号,对任一结点i(1<=i<=n)有以下性质:
- 如果i =1,则结点i是二叉树的根,无双亲;如果i >1,则其双亲是结点
- 如果2i > n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i
- 如果2i+1 >n,则结点i无右孩子;否则其右孩子是结点2i+1
4、存储结构
(1)顺序存储
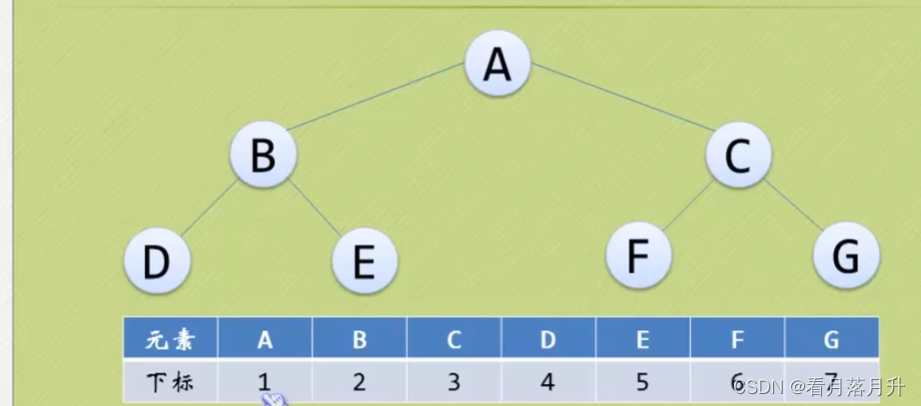
对于完全二叉树是十分方便的,但是一般二叉树就不行了,空间会造成极大的浪费
(2)链式存储!!!!
结点结构

代码
typedef struct BiNode {int data;struct BiTNode* lchild, * rchild;
}BiTNode,*BiTree;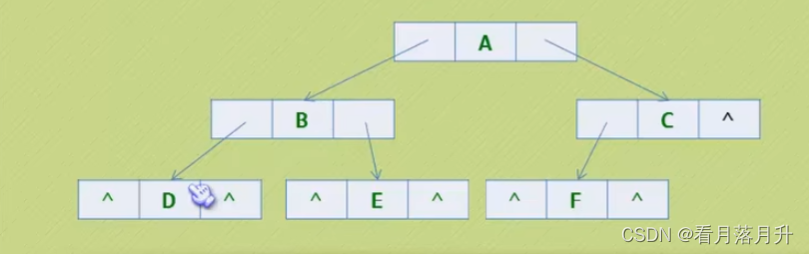
5、二叉树的遍历
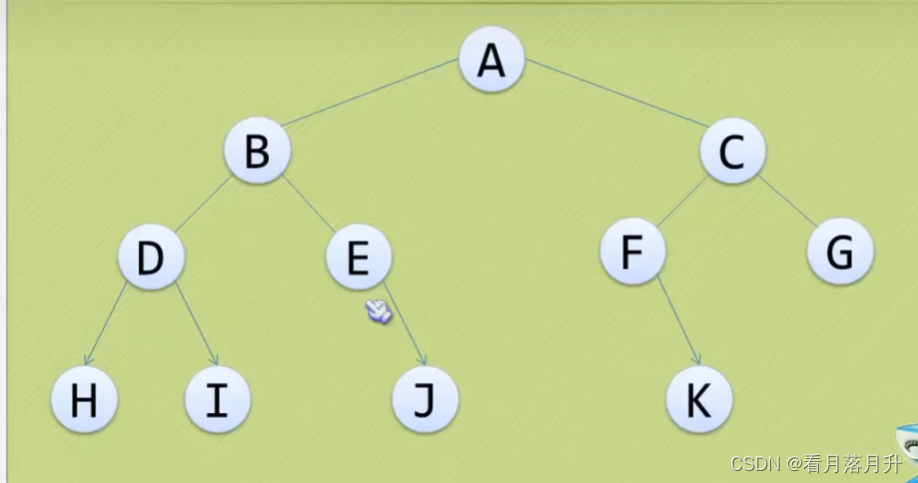
(1)先序遍历
根——>左子树——>右子树
ABDHIEJCFKG
(2)中序遍历
左子树——>根——>右子树
HDIBEGAFKCG
(3)后序遍历
左子树——>右子树——>根
HIDJEBKFGCA
(4)层序遍历
ABCDEFGHIJK
八、二叉树的建立和遍历算法
代码(包括递归和非递归遍历):
#define _CRT_SECURE_NO_WARNINGS 1;
#include <stdio.h>
#include <stdlib.h> typedef struct TreeNode {char val;struct TreeNode* left;struct TreeNode* right;
} TreeNode;TreeNode* createTree(char** str) {//*str就是 char数组的指针if (**str == '#') {(*str)++; //指针偏移return NULL;}TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));node->val = **str;(*str)++;//这里递归实现,从根节点开始往左子树里填node->left = createTree(str);node->right = createTree(str);return node;
}// 递归遍历
void preOrderRecursive(TreeNode* root) {if (root == NULL) return;printf("%c ", root->val);preOrderRecursive(root->left);preOrderRecursive(root->right);
}void inOrderRecursive(TreeNode* root) {if (root == NULL) return;inOrderRecursive(root->left);printf("%c ", root->val);inOrderRecursive(root->right);
}void postOrderRecursive(TreeNode* root) {if (root == NULL) return;postOrderRecursive(root->left);postOrderRecursive(root->right);printf("%c ", root->val);
}// 非递归遍历使用栈来辅助
#define MAX_SIZE 100
typedef struct {TreeNode* data[MAX_SIZE];int top;
} Stack;void initStack(Stack* s) {s->top = -1;
}int isEmpty(Stack* s) {return s->top == -1;
}int isFull(Stack* s) {return s->top == MAX_SIZE - 1;
}void push(Stack* s, TreeNode* node) {if (isFull(s)) return;s->data[++(s->top)] = node;
}TreeNode* pop(Stack* s) {if (isEmpty(s)) return NULL;return s->data[(s->top)--];
}void preOrderNonRecursive(TreeNode* root) {if (root == NULL) return;Stack s;initStack(&s);push(&s, root);while (!isEmpty(&s)) {TreeNode* node = pop(&s);printf("%c ", node->val);if (node->right) push(&s, node->right);if (node->left) push(&s, node->left);}
}void inOrderNonRecursive(TreeNode* root) {Stack s;initStack(&s);TreeNode* cur = root;while (cur || !isEmpty(&s)) {while (cur) {push(&s, cur);cur = cur->left;}cur = pop(&s);printf("%c ", cur->val);cur = cur->right;}
}void postOrderNonRecursive(TreeNode* root) {if (root == NULL) return;Stack s1, s2;initStack(&s1);initStack(&s2);push(&s1, root);while (!isEmpty(&s1)) {TreeNode* node = pop(&s1);push(&s2, node);if (node->left) push(&s1, node->left);if (node->right) push(&s1, node->right);}while (!isEmpty(&s2)) {TreeNode* node = pop(&s2);printf("%c ", node->val);}
}int main() {char input[101];scanf("%s", input);char* str = input;TreeNode* root = createTree(&str);// 递归遍历 preOrderRecursive(root);printf("\n");inOrderRecursive(root);printf("\n");postOrderRecursive(root);printf("\n");// 非递归遍历 preOrderNonRecursive(root);printf("\n");inOrderNonRecursive(root);printf("\n");postOrderNonRecursive(root);printf("\n");return 0;
}
这里的递归好理解,对于非递归
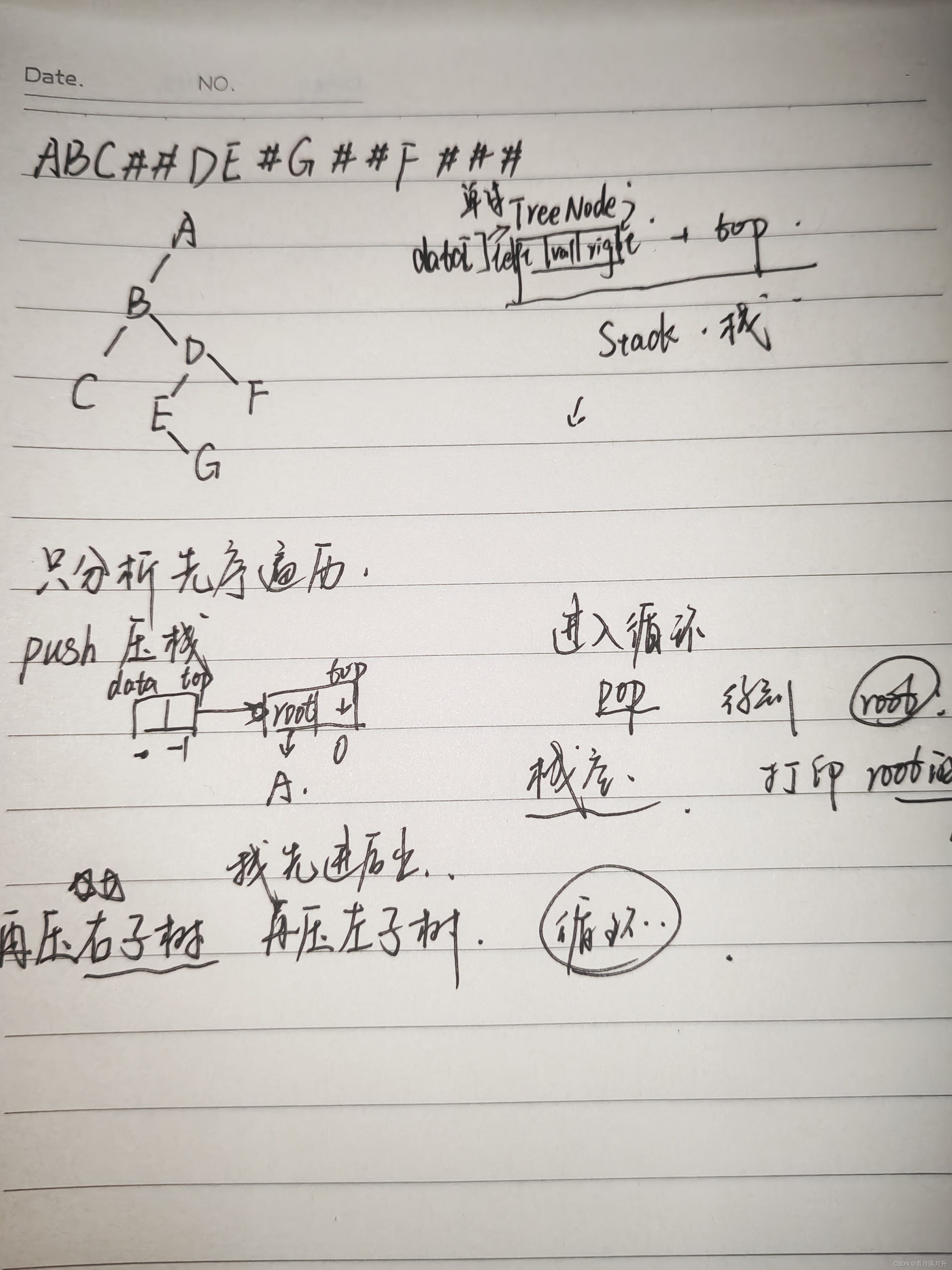
九、线索二叉树

结构体
//二叉树的二又线索存储表示
typedef struct BiThrNode{TElemType data;struct BiThrNode *lchild, *rchild;int LTag, RTag;
}BiThrNode, *BiThrTree;用实线表示孩子节点,虚线表示前驱后继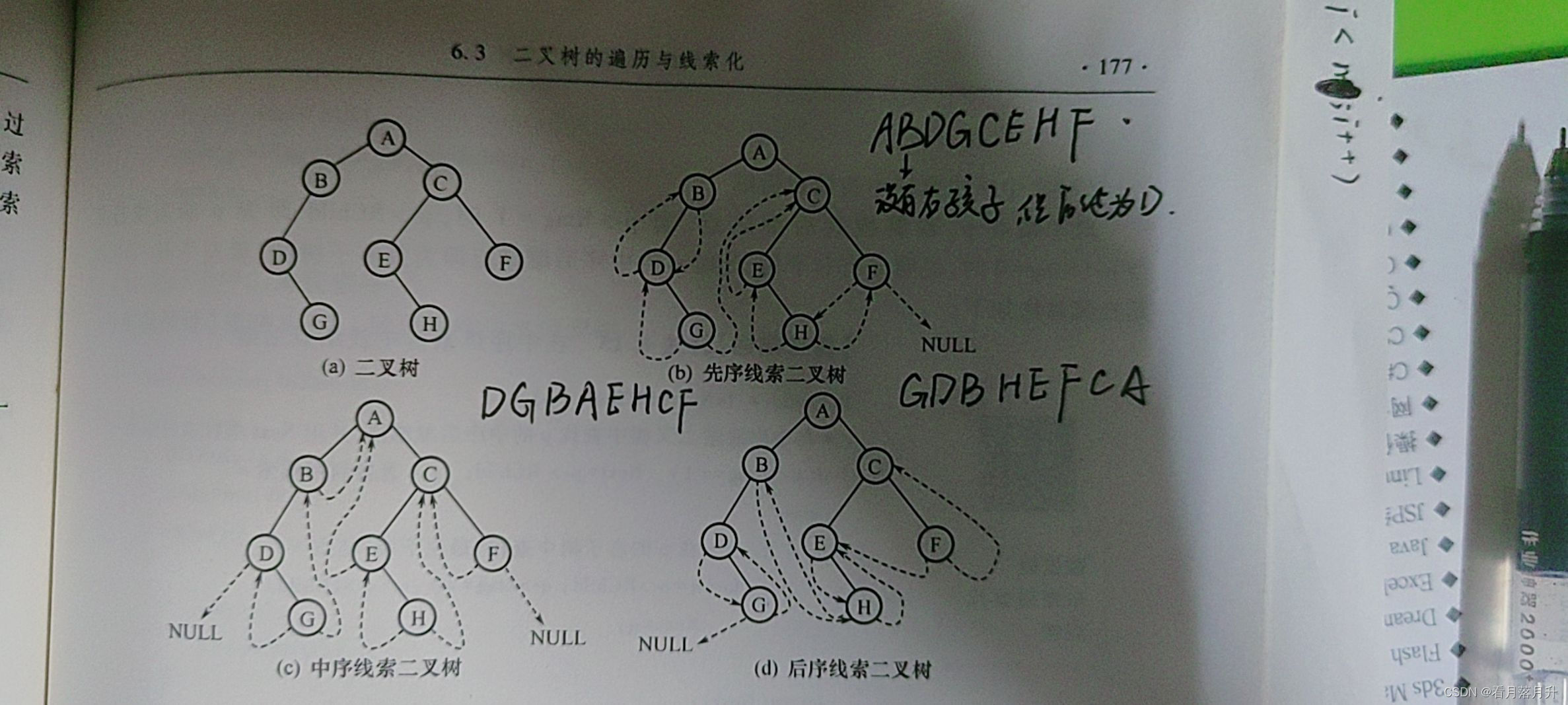
中序线索代码实现
结构体
typedef struct Thread {struct Thread* left_node, * right_node;//左右指针int data;//需要存放的数据/*默认0代表左右孩子 1代表前驱或者后继*/int left_type;//类型标志int right_type;//类型标志
}Node;Node* pre;//前驱结点的变量
Node* head;//头指针 指向某种遍历的第一个结点线索化
void inOrderThreadTree(Node* node)
{//如果当前结点为NULL 直接返回if (node == NULL) {return;}//先处理左子树inOrderThreadTree(node->left_node);if (node->left_node == NULL){//设置前驱结点node->left_type = 1;node->left_node = pre;}//如果结点的右子节点为NULL 处理前驱的右指针if (pre !=NULL && pre->right_node == NULL){//设置后继pre->right_node = node;pre->right_type = 1;}//每处理一个节点 当前结点是下一个节点的前驱pre = node;//最后处理右子树inOrderThreadTree(node->right_node);
}遍历
void inOrderTraverse(Node* root)
{//从根节点开始先找到最左边if (root == NULL){return;}Node* temp = root;//先找到最左边结点 然后根据线索化直接向右遍历while (temp != NULL && temp->left_type == 0){temp = temp->left_node;}while (temp != NULL){//输出temp = temp->right_node;}
}这里停一下,时间不多,前驱后继就不写了哈
十、树、森林继二叉树的相互转换
1、树转换为二叉树
树转换成相应的二叉树分两个步骤:
- 在树中所有的兄弟结点之间加一连线
- 对每个结点,除了保留与其长子的连线外,去掉该结点与其他孩子的连线
只有左子树
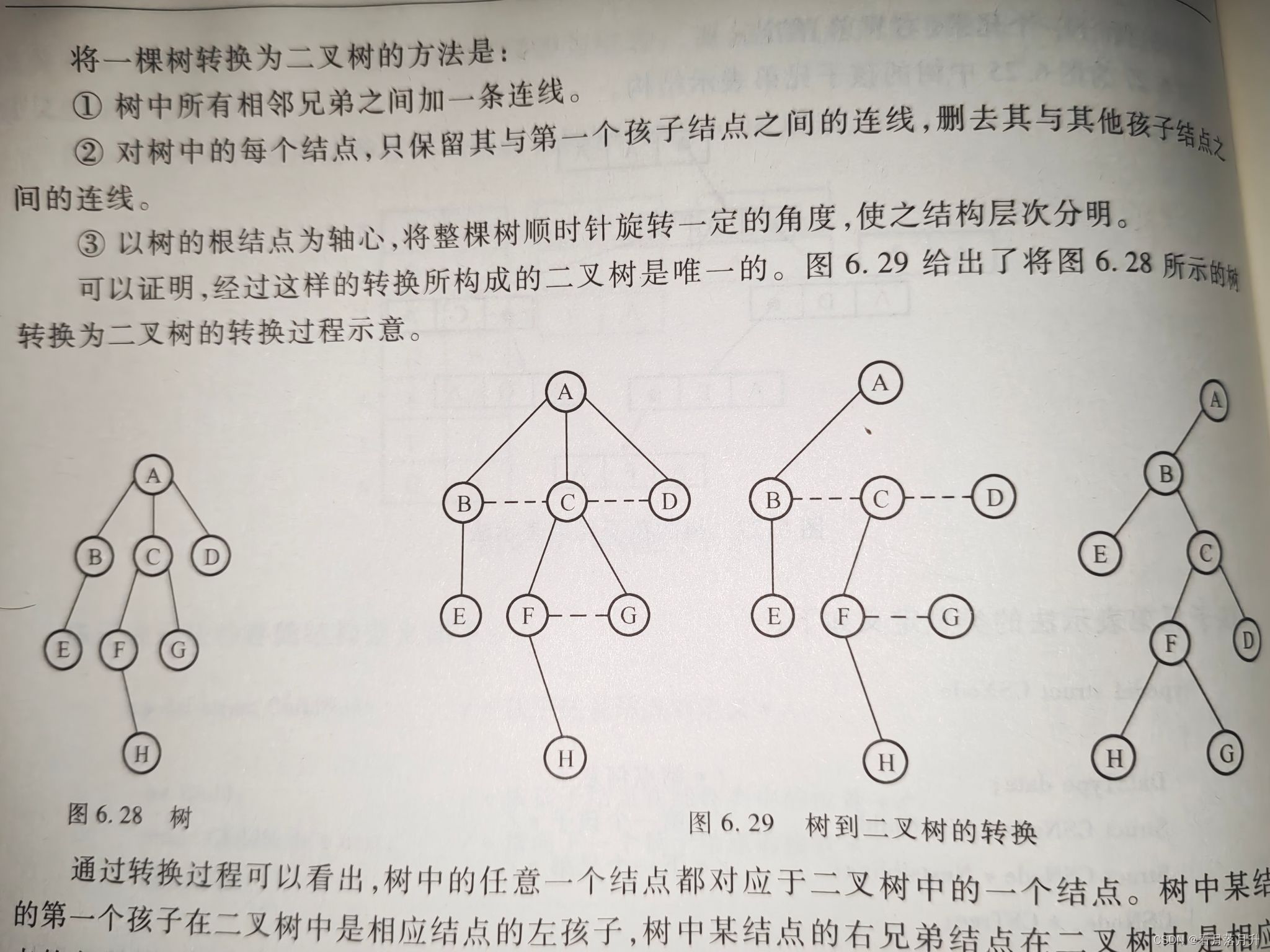
2、森林到二叉树的转换
森林转换为二叉树分两个步骤:
- 先将森林中的每棵树变为二叉树
- 再将各二叉树的根结点视为兄弟从左至右连在一起,就形成了一棵二叉树
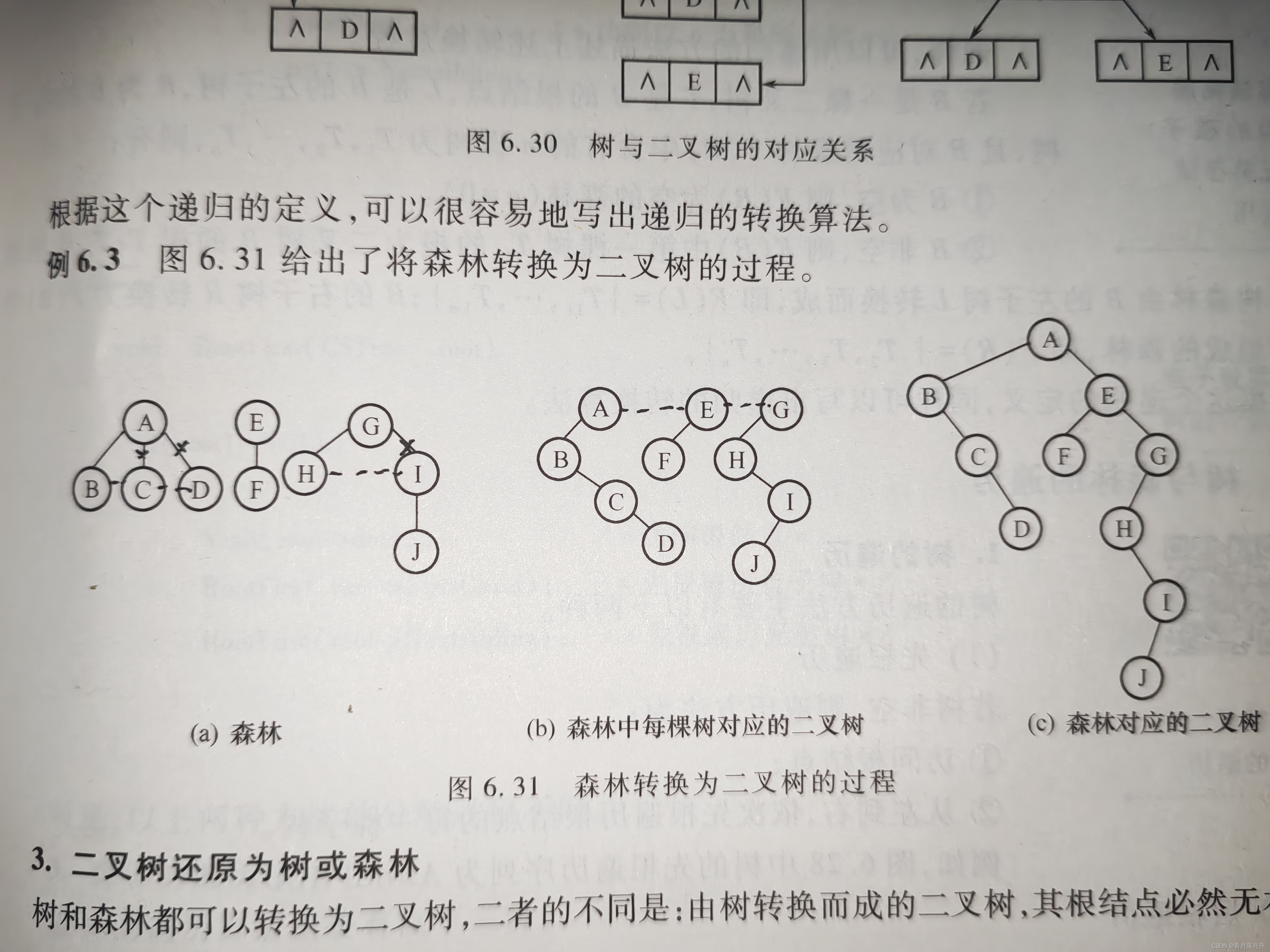
3、二叉树到树、森林的转换
- 若结点x是其双亲y的左孩子,则把x的右孩子,右孩子的右孩子,…,都与y用连线连起来。
- 去掉所有双亲到右孩子之间的连线
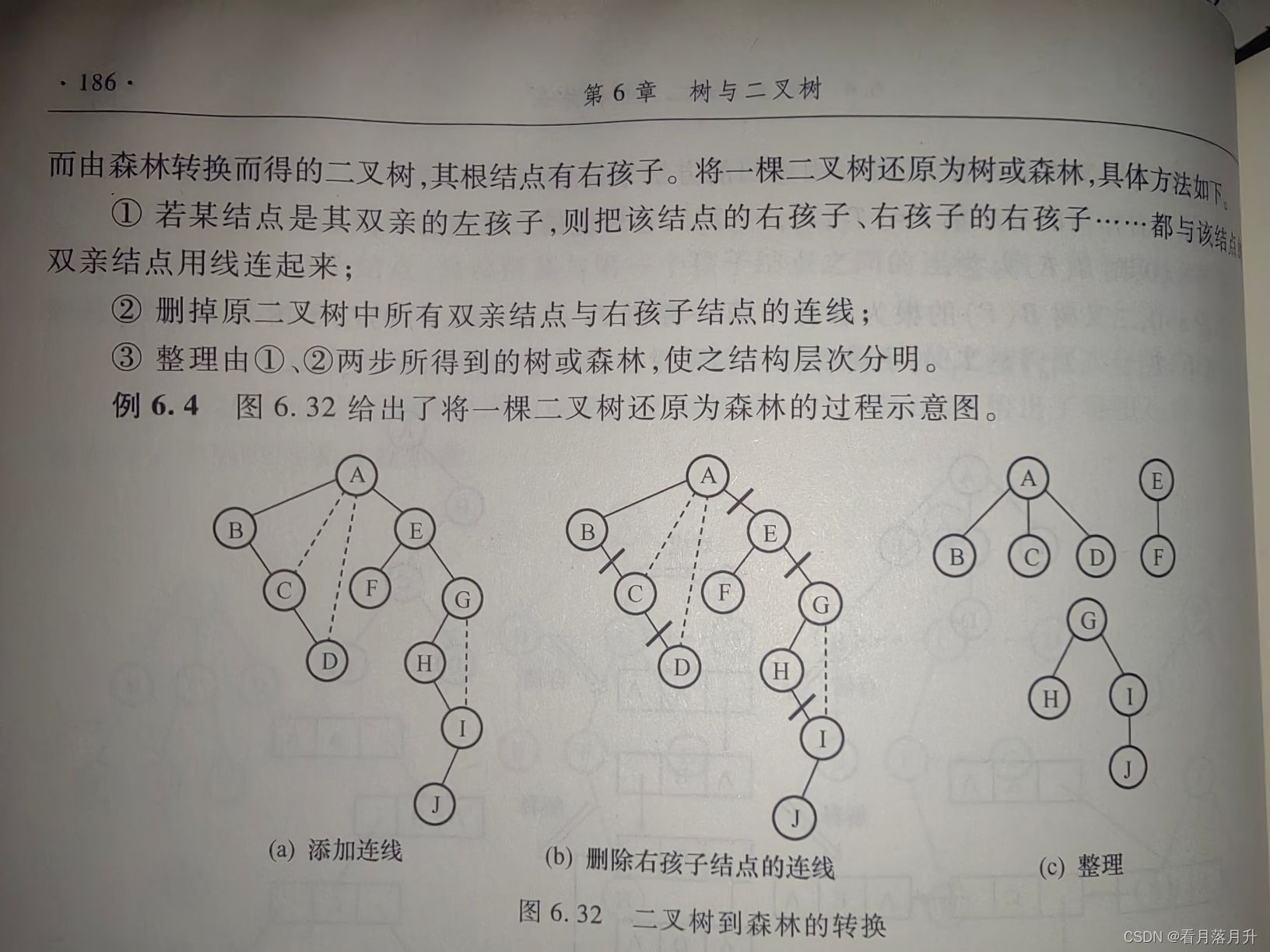
4、树与森林的遍历
树的遍历分为两种方式:一种是先根遍历,另一种是后根遍历。
- 先根遍历:先访问树的根结点,然后再依次先根遍历根的每棵子树。
- 后根遍历:先依次遍历每棵子树,然后再访问根结点。
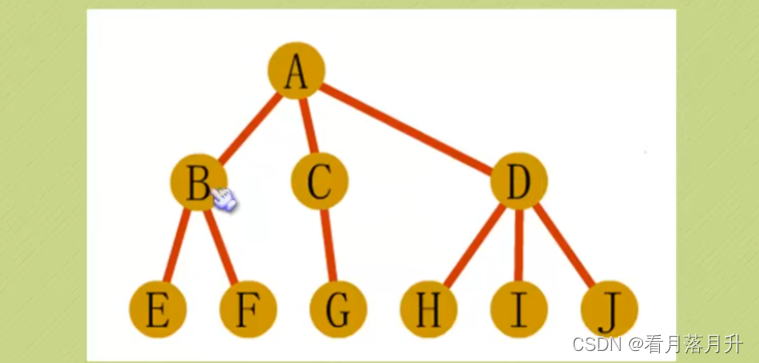
先根遍历:ABEFCGDHIJ
后根遍历:EFBGCHIJDA
森林的遍历也分为前序遍历和后序遍历,其实就是按照树的先根遍历和后根遍历依次访问森林的每一棵树。
我们的惊人发现:树、森林的前根(序)遍历和二叉树的前序遍历结果相同,树、森林的后根(序)遍历和二叉树的中序遍历结果相同!
十一、哈夫曼树
1、定义
我们先把这两棵二叉树简化成叶子结点带权的二叉树(注:树结点间的连线相关的数叫做权,Weight) 。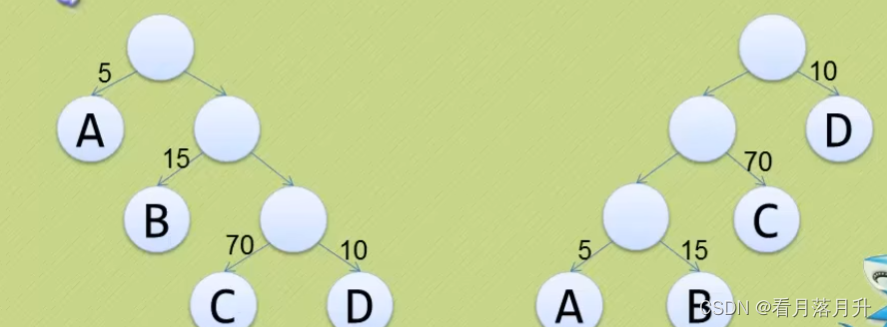
- 结点的路径长度:从根结点到该结点的路径上的连接数。 第一幅图C的就是3
- 树的路径长度:树中每个叶子结点的路径长度之和。 第一幅图为1+2+3+3 = 9
- 结点带权路径长度:结点的路径长度与结点权值的乘积。 第一幅图C的就是3*70=210
- 树的带权路径长度:-WPL(Weighted Path Length)是树中所有叶子结点的带权路径长度之和。第一幅图为1*5+2*15+3*70+3*10 = 275
WPL的值越小,说明构造出来的二叉树性能越优。
构造过程:
1、构造森林全是根; 2、选用两小造新树;
3、删除两小添新人 ;4、重复2、3剩单根。
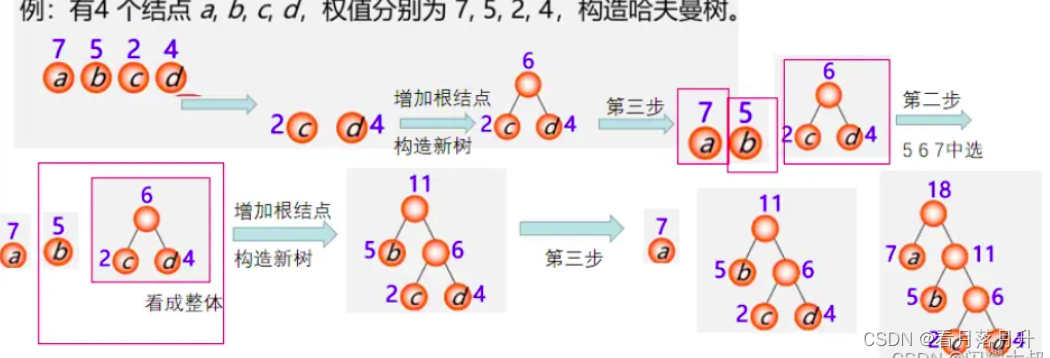
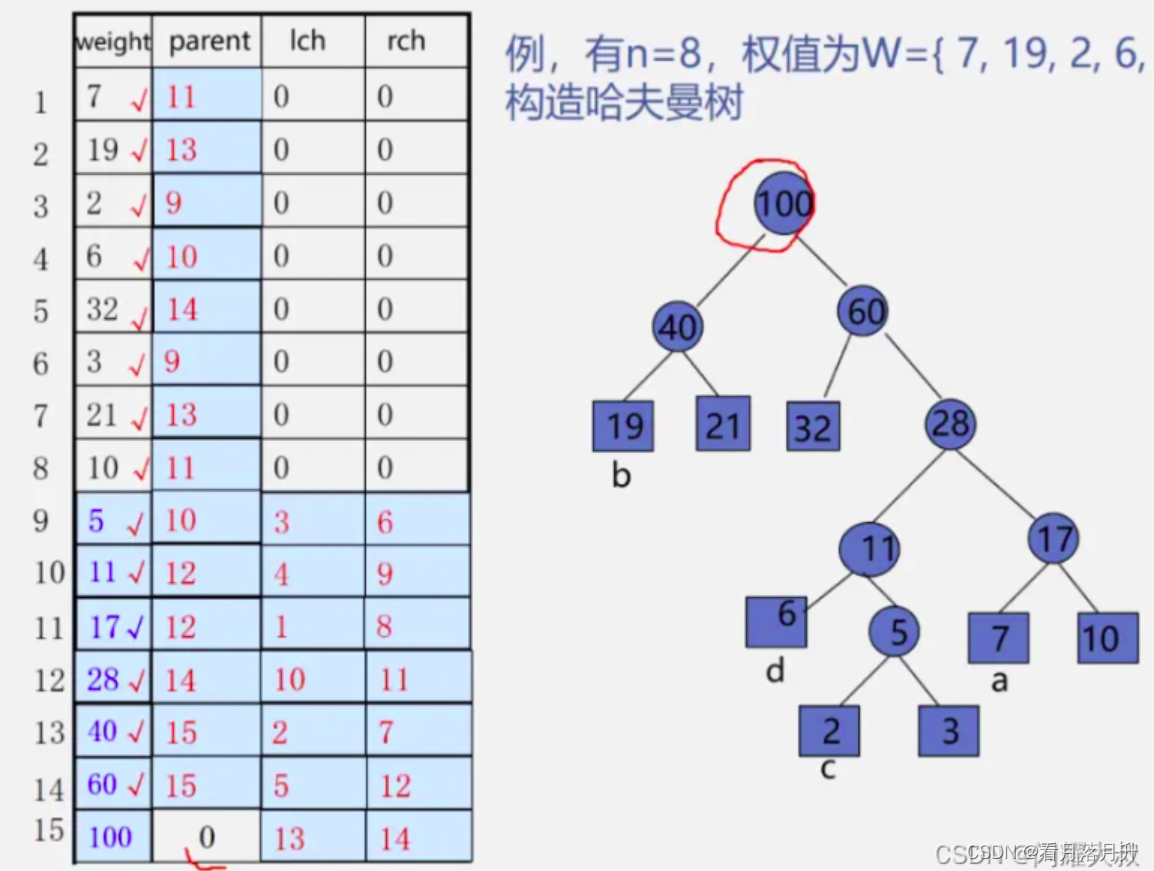
2、哈夫曼树的构建
结构体
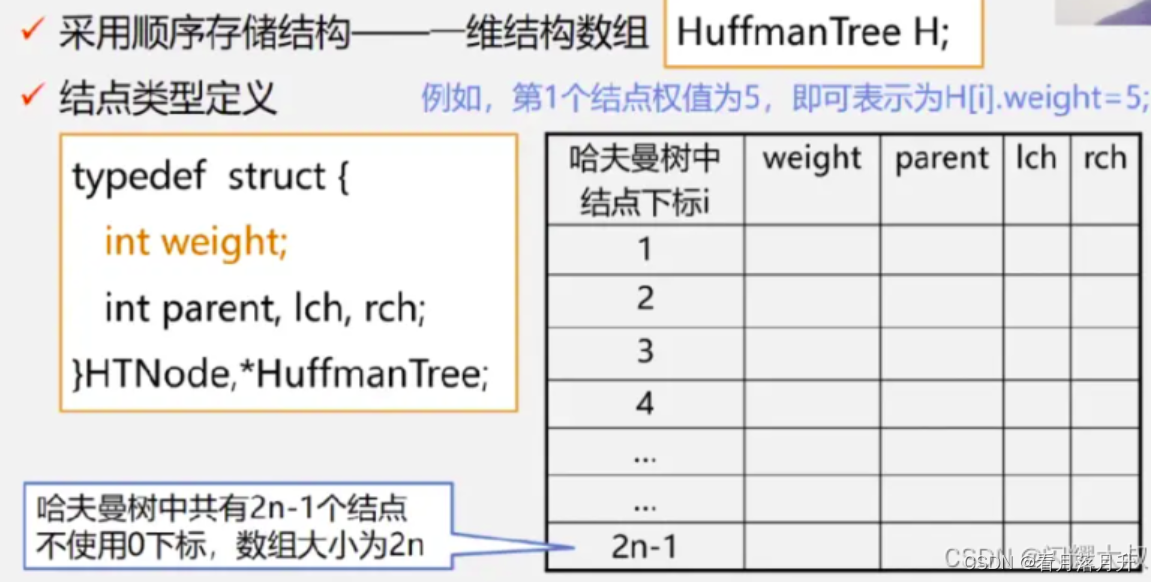
//哈夫曼树结点结构
typedef struct {int weight;//结点权重int parent, left, right;//父结点、左孩子、右孩子在数组中的位置下标
}HTNode, *HuffmanTree;构建
//HT为地址传递的存储哈夫曼树的数组,w为存储结点权重值的数组,n为结点个数
void CreateHuffmanTree(HuffmanTree *HT, int *w, int n)
{if(n<=1) return; // 如果只有一个编码就相当于0int m = 2*n-1; // 哈夫曼树总节点数,n就是叶子结点*HT = (HuffmanTree) malloc((m+1) * sizeof(HTNode)); // 0号位置不用HuffmanTree p = *HT;// 初始化哈夫曼树中的所有结点for(int i = 1; i <= n; i++){(p+i)->weight = *(w+i-1);(p+i)->parent = 0;(p+i)->left = 0;(p+i)->right = 0;}//从树组的下标 n+1 开始初始化哈夫曼树中除叶子结点外的结点for(int i = n+1; i <= m; i++){(p+i)->weight = 0;(p+i)->parent = 0;(p+i)->left = 0;(p+i)->right = 0;}//构建哈夫曼树for(int i = n+1; i <= m; i++){int s1, s2;Select(*HT, i-1, &s1, &s2);(*HT)[s1].parent = (*HT)[s2].parent = i;(*HT)[i].left = s1;(*HT)[i].right = s2;(*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;}
}3、重难点:哈夫曼编码
1. 计算字符串中每个字符的频率
2. 按照字符出现的频率进行排序,组成一个队列 Q
3. 把这些字符作为叶子节点开始构建一棵哈夫曼树
4. 对字符进行编码

哈夫曼树和编码都不唯一!只有树的WPL(带权路径长度)才是唯一的!
代码实现:
#include <stdio.h>
#include <stdlib.h>// 定义哈夫曼树节点结构
typedef struct HuffmanNode {char data; // 字符int freq; // 频率struct HuffmanNode* left, * right; // 左右子节点
} HuffmanNode;// 定义优先级队列结构
typedef struct PriorityQueue {int size; // 队列当前大小int capacity; // 队列容量HuffmanNode** array; // 存储哈夫曼树节点的数组指针
} PriorityQueue;// 创建哈夫曼树节点
HuffmanNode* createNode(char data, int freq) {HuffmanNode* node = (HuffmanNode*)malloc(sizeof(HuffmanNode)); // 分配内存空间node->data = data; // 设置节点字符node->freq = freq; // 设置节点频率node->left = node->right = NULL; // 初始化左右子节点为空return node; // 返回节点指针
}// 创建优先级队列
PriorityQueue* createPriorityQueue(int capacity) {PriorityQueue* queue = (PriorityQueue*)malloc(sizeof(PriorityQueue)); // 分配内存空间queue->size = 0; // 初始化队列大小为0queue->capacity = capacity; // 设置队列容量queue->array = (HuffmanNode**)malloc(queue->capacity * sizeof(HuffmanNode*)); // 分配内存空间return queue; // 返回队列指针
}// 交换两个节点
void swapNodes(HuffmanNode** a, HuffmanNode** b) {HuffmanNode* temp = *a;*a = *b;*b = temp;
}// 向下堆化
void minHeapify(PriorityQueue* queue, int idx) {int smallest = idx;int left = 2 * idx + 1; // 计算左子节点索引int right = 2 * idx + 2; // 计算右子节点索引// 找出三个节点中最小的节点if (left < queue->size && queue->array[left]->freq < queue->array[smallest]->freq) {smallest = left;}if (right < queue->size && queue->array[right]->freq < queue->array[smallest]->freq) {smallest = right;}// 如果最小节点不是当前节点,交换节点并递归向下堆化if (smallest != idx) {swapNodes(&queue->array[idx], &queue->array[smallest]);minHeapify(queue, smallest);}
}// 插入节点
void insertNode(PriorityQueue* queue, HuffmanNode* node) {queue->size++; // 队列大小加1int i = queue->size - 1; // 获取最后一个位置的索引queue->array[i] = node; // 将节点插入最后一个位置// 如果插入节点的频率小于父节点的频率,向上调整while (i && queue->array[i]->freq < queue->array[(i - 1) / 2]->freq) {swapNodes(&queue->array[i], &queue->array[(i - 1) / 2]);i = (i - 1) / 2;}
}// 提取最小节点
HuffmanNode* extractMin(PriorityQueue* queue) {if (queue->size == 0) return NULL; // 如果队列为空,返回空指针HuffmanNode* root = queue->array[0]; // 获取根节点queue->array[0] = queue->array[queue->size - 1]; // 将最后一个节点移到根节点位置queue->size--; // 队列大小减1minHeapify(queue, 0); // 向下堆化return root; // 返回根节点
}// 构建哈夫曼树
HuffmanNode* buildHuffmanTree(char data[], int freq[], int size) {PriorityQueue* queue = createPriorityQueue(size); // 创建优先级队列// 将字符和频率构建成哈夫曼树节点,并插入优先级队列中for (int i = 0; i < size; i++) {insertNode(queue, createNode(data[i], freq[i]));}// 从优先级队列中不断取出最小的两个节点,构建哈夫曼树,直到队列中只剩一个节点while (queue->size != 1) {HuffmanNode* left = extractMin(queue);HuffmanNode* right = extractMin(queue);// 创建新节点作为父节点,频率为左右子节点频率之和HuffmanNode* top = createNode('\0', left->freq + right->freq);top->left = left;top->right = right;// 插入新节点到队列中insertNode(queue, top);}// 返回根节点return extractMin(queue);
}// 打印哈夫曼编码
void printHuffmanCodes(HuffmanNode* root, int arr[], int top) {// 遍历树,生成编码if (root->left) {arr[top] = 0;printHuffmanCodes(root->left, arr, top + 1);}if (root->right) {arr[top] = 1;printHuffmanCodes(root->right, arr, top + 1);}// 当遍历到叶子节点时,打印字符及其编码if (!root->left && !root->right) {printf("%c: ", root->data);for (int i = 0; i < top; i++) {printf("%d", arr[i]);}printf("\n");}
}// 主函数
int main() {char data[] = { 'a', 'b', 'c', 'd', 'e', 'f' }; // 字符集合int freq[] = { 5, 9, 12, 13, 16, 45 }; // 字符频率int size = sizeof(data) / sizeof(data[0]); // 字符集合大小// 构建哈夫曼树HuffmanNode* root = buildHuffmanTree(data, freq, size);int arr[100]; // 存储编码的数组int top = 0; // 记录编码// 打印哈夫曼编码printf("哈夫曼编码:\n");printHuffmanCodes(root, arr, top);return 0;
}

有点难,啧,我再想想
相关文章:

数据结构6---树
一、定义 树(Tree)是n(n>0)个结点的有限集。当n0时成为空树,在任意一棵非空树中: 1、有且仅有一个特定的称为根(Root)的结点; 2、当n>1时,其余结点可分为m(m>日)个互不相交的有限集T1、T2、...、 Tm,其中每一个集合本身又是一棵树,并且称为根的…...
一键制作,打造高质量的数字刊物
随着数字化时代的到来,数字刊物已经成为信息传播的重要载体。它以便捷、环保、互动性强等特点,受到了越来越多人的青睐。然而,如何快速、高效地制作出高质量的数字刊物,成为许多创作者面临的难题。今天,教大家一个制作…...

Java面试题:对比继承Thread类和实现Runnable接口两种创建线程的方法,以及它们的优缺点
Java 中创建线程有两种主要的方法:继承 Thread 类和实现 Runnable 接口。下面我将分别介绍这两种方法,并对比它们的优缺点。 继承 Thread 类 方法: 创建一个继承自 Thread 的子类。重写 Thread 类的 run 方法。创建子类的实例并调用 start…...

编译原理-各章典型题型+思路求解
第2章文法和语言习题 基础知识: 思路: 基础知识: 思路: 基础知识: 编译原理之 短语&直接短语&句柄 定义与区分_编译原理短语,直接短语,句柄-CSDN博客 思路: 题目: 基础解释:…...

【绝对有用】C++ vector排序
在 C 中,有多种方法可以对向量(即 std::vector)进行排序。最常用的方法是使用标准库中的 std::sort 函数。以下是一些例子: 使用 std::sort 函数 std::sort 函数是标准库 <algorithm> 中的一个函数,可以对向量…...

linux——VScode安装
方法一:使用snap一键安装 Snap Store 是 Ubuntu、Debian、Fedora 和其他几个 Linux 发行版中的一个应用商店,提供了数千个应用程序和工具的安装。Snap Store 使用 Snap 包格式,这是一种通用的 Linux 软件包格式,使得在不同的 Lin…...

X-LoRA:高效微调 LoRA 系列,实现不同领域知识专家混合模型
📜 文献卡 X-LoRA: Mixture of Low-Rank Adapter Experts, a Flexible Framework for Large Language Models with Applications in Protein Mechanics and Molecular Design作者: Eric L. Buehler; Markus J. BuehlerDOI: 10.48550/arXiv.2402.07148摘要:We report…...

基于卷积神经网络的目标检测
卷积神经网络基础知识 1.什么是filter 通常一个6x6的灰度图像,构造一个3*3的矩阵,在卷积神经网络中称之为filter,对6x6的图像进行卷积运算。 2.什么是padding 假设输出图像大小为nn与过滤器大小为ff,输出图像大小则为(n−f1)∗(…...

Mysqld数据库管理
一.Mysqld数据库类型 常用的数据类型 int 整型 无符号[0-4294967296(2的32次方)-1],有符号[-2147483648(2的31次方)-2147483647]float单精度浮点 4字节32位double双精度浮点 8字节64位char固定长度的字符类型…...
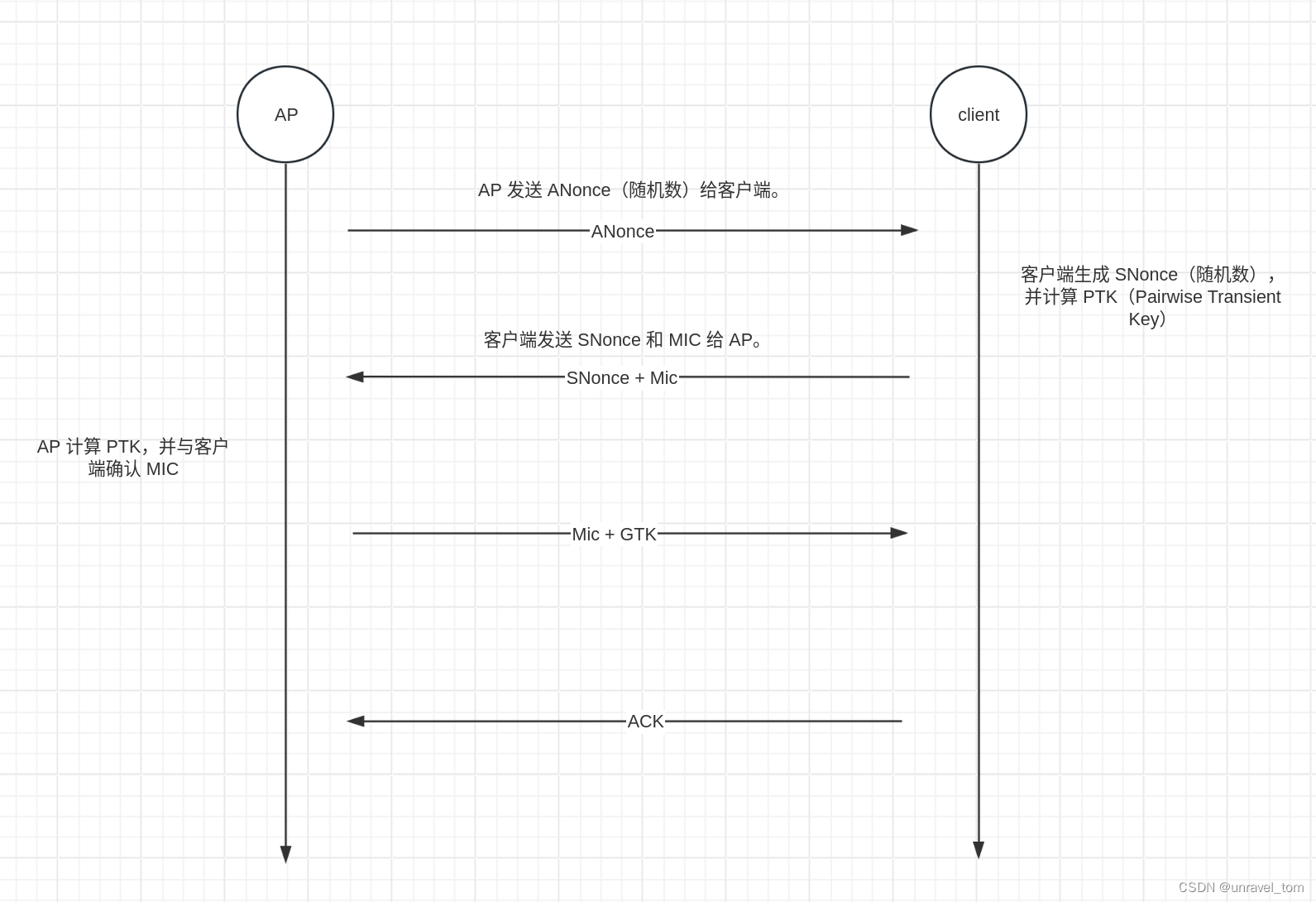
Wifi通信协议:WEP,WPA,WPA2,WPA3,WPS
前言 无线安全性是保护互联网安全的重要因素。连接到安全性低的无线网络可能会带来安全风险,包括数据泄露、账号被盗以及恶意软件的安装。因此,利用合适的Wi-Fi安全措施是非常重要的,了解WEP、WPA、WPA2和WPA3等各种无线加密标准的区别也是至…...

开源【汇总】
开源【汇总】 前言版权推荐开源【汇总】最后 前言 先占个位 2024-6-21 21:29:33 以下内容源自《【创作模板】》 仅供学习交流使用 版权 禁止其他平台发布时删除以下此话 本文首次发布于CSDN平台 作者是CSDN日星月云 博客主页是https://jsss-1.blog.csdn.net 禁止其他平台发…...

英文字母表
目录 一 设计原型 二 后台源码 一 设计原型 二 后台源码 namespace 英文字母表 {public partial class Form1 : Form{public Form1(){InitializeComponent();}private void Form1_Load(object sender, EventArgs e){foreach (var item in panel1.Controls){if (item ! null)…...

Redis缓存穿透
缓存穿透: 查询一个不存在的数据,mysql查询不到数据也不会直接写入缓存,就会导致每次请求都查数据库。 方法一: 方法二: 布隆过滤器: 简单来说就是一个二进制数组,用0和1来判断数组中是否存在…...
正则表达式)
SHELL脚本学习(十一)正则表达式
一、锚点字符 1.1 锚点行首 脱字符(^)指出行首位置 $ cat < file1 test line1 test line2 test line3 line4 test#打印所有包括文本 test的行 $ sed -n /test/p file1 test line1 test line2 test line3 line4 test#打印所有以test为首的行 $ sed -n /^test/p file1 test…...

Leetcode Java学习记录——代码随想录哈希表篇
文章目录 哈希表几种哈希实现 Java数组HashSetmap方法charAt()toCharArray()for 遍历长度 哈希表 当需要快速判断一个元素是否出现在集合里的时候,就要用到哈希表。 无限循环就意味着重复出现。 几种哈希实现 数组:大小固定set:只存keymap…...

我又挖到宝了!小米、352、希喂宠物空气净化器除毛能力PK
养宠家庭常常因为猫咪们掉毛的问题烦恼。无论是短毛猫还是长毛猫,它们的毛发总是无处不在,从沙发到地毯,从床铺到衣物,甚至飘散在空气中。其中最难清理的就是飘浮在空气中的浮毛,最让人担心的是,空气中的浮…...

每月 GitHub 探索|10 款引领科技趋势的开源项目
1.IT-Tools 仓库名称: CorentinTh/it-tools 截止发稿星数: 16842 (近一个月新增:5744) 仓库语言: Vue 仓库开源协议: GNU General Public License v3.0 引言 CorentinTh/it-tools 是一个开源项目,提供各种对开发者友好的在线工具࿰…...

【如何让新增的Android.mk参与编译】
步骤1: 你需要在你新增的Android.mk目录以上的位置找一个已有的Android.mk 步骤2: 在原本已有的Android.mk中加入: //这是你新增的Android.mk文件的路径 include $(LOCAL_PATH)/xxx/xxx/Android.mk如果有些多可以这样写 //dir1 dir2是你新…...

【windows|009】计算机网络基础知识
🍁博主简介: 🏅云计算领域优质创作者 🏅2022年CSDN新星计划python赛道第一名 🏅2022年CSDN原力计划优质作者 🏅阿里云ACE认证高级工程师 🏅阿里云开发者社区专家博主 💊交流社…...

C语言循环中获取之前变量的值
获取上个数组变量的值 #include <stdio.h> #include <string.h>enum { GG, DD }; int main() {int bi[] {0, 0};int bi_s1[] {0, 0};for (int i 0; i < 5; i) {memcpy(bi_s1, bi, sizeof(bi));bi[GG] i * 3;bi[DD] i * 2;printf("bigg %d, bigg_s1 …...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

