【C++】平衡二叉树(AVL树)的实现
目录
- 一、AVL树的概念
- 二、AVL树的实现
- 1、AVL树的定义
- 2. 平衡二叉树的插入
- 2.1 按照二叉排序树的方式插入并更新平衡因子
- 2.2 AVL树的旋转
- 2.2.1 新节点插入较高左子树的左侧(LL平衡旋转)
- 2.2.2 新节点插入较高右子树的右侧(RR平衡旋转)
- 2.2.3 新节点插入较高左子树的右侧(LR平衡旋转)
- 2.2.4 新节点插入较高右子树的左侧(RL平衡旋转)
- 2.2.5 总结
- 3 平衡二叉树的删除(了解即可)
- 4 平衡二叉树的验证
- 三、平衡二叉树的效率分析
一、AVL树的概念
二叉排序树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。
为了避免树的高度增长过快,降低二叉排序树的性能,规定在插入和删除结点时,要保证任意结点的左、右子树高度差的绝对值不超过1,将这样的二叉树称为平衡二叉树,也称AVL树。
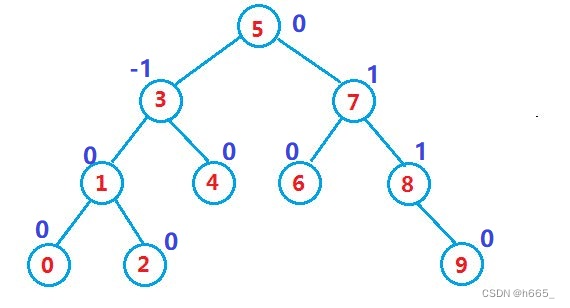
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
二、AVL树的实现
1、AVL树的定义
AVL树结点的定义:
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent; // 使用三叉链方便后续处理,但要记得维护pair<K, V> _kv; // 保存键值对int _bf; // 平衡因子
};
2. 平衡二叉树的插入
2.1 按照二叉排序树的方式插入并更新平衡因子
AVL树就是在二叉排序树的基础上加上了平衡因子,因此AVL树也可以看成是二叉排序树。那么AVL树的插入过程可以分为两步:
(1) 按照二叉排序树的方法插入新结点
(2) 调整结点的平衡因子
bool Insert(const pair<K, V>& kv)
{// 先按照二叉排序树的方法进行结点插入if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while(cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(kv);if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;// 新结点插入后,AVL树的平衡性可能会遭到破坏,此时就需要更新平衡因子,并检测是否// 破坏了AVL树的平衡性while (parent){/*cur插入后,parent的平衡因子一定需要调整,在插入之前,parent的平衡因子分为三种情况:-1,0, 1, 分以下两种情况:1. 如果cur插入到parent的左侧,只需给parent的平衡因子-1即可2. 如果cur插入到parent的右侧,只需给parent的平衡因子+1即可*/if (parent->_left == cur){--parent->_bf;}else{++parent->_bf;}/*此时:parent的平衡因子可能有三种情况:0,正负1, 正负21. 如果parent的平衡因子为0,说明插入之前parent的平衡因子为正负1,插入后被调整成0,此时满足AVL树的性质,插入成功2. 如果parent的平衡因子为正负1,说明插入前parent的平衡因子一定为0,插入后被更新成正负1,此时以parent为根的树的高度增加,需要继续向上更新3. 如果parent的平衡因子为正负2,则parent的平衡因子违反平衡树的性质,需要对其进行旋转处理*/if (0 == parent->_bf){break;}else if (1 == parent->_bf || -1 == parent->_bf){cur = cur->_parent;parent = parent->_parent;}else if (2 == parent->_bf || -2 == parent->_bf){// 旋转处理}else{// 如果平衡因子不是以上几种情况,说明代码逻辑错误assert(false);}}return true;
}
2.2 AVL树的旋转
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:LL平衡旋转(右旋),RR平衡旋转(左旋),LR平衡旋转(先左旋后右旋),RL平衡旋转(先右旋后左旋)
2.2.1 新节点插入较高左子树的左侧(LL平衡旋转)
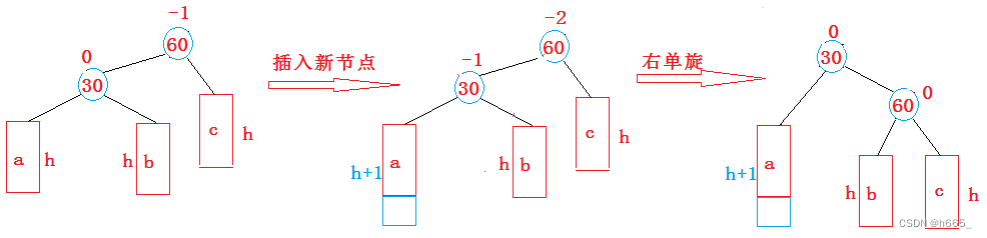
上图在插入前,AVL树是平衡的,新节点插入到30的左子树(注意:此处不是左孩子)中,30左子树增加了一层,导致以60为根的二叉树不平衡,要让60平衡,只能将60左子树的高度减少一层,右子树增加一层,即将左子树往上提,这样60转下来,因为60比30大,只能将其放在30的右子树,而如果30有右子树,右子树根的值一定大于30,小于60,只能将其放在60的左子树,旋转完成后,更新节点的平衡因子即可。
在旋转过程中,有以下几种情况需要考虑:
- 30节点的右孩子可能存在,也可能不存在
- 60可能是根节点,也可能是子树
如果是根节点,旋转完成后,要更新根节点
如果是子树,可能是某个节点的左子树,也可能是右子树
void RotateR(Node* parent)
{// subL:parent的左孩子// subLR:parent的左孩子的右孩子,注意:该点可能不存在Node* subL = parent->_left;Node* subLR = subL->_right;subL->_right = parent;parent->_left = subLR;Node* ppnode = parent->_parent; // 记录parent的父结点,用于连接新的子树parent->_parent = subL;if (subLR){subLR->_parent = parent;}if (ppnode == nullptr){_root = subL;_root->_parent = nullptr;}else {if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}// 根据调整后的结构更新部分节点的平衡因子subL->_bf = parent->_bf = 0;
}
2.2.2 新节点插入较高右子树的右侧(RR平衡旋转)
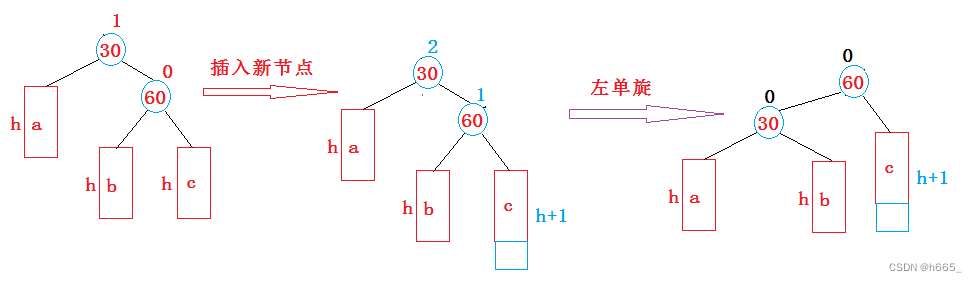
具体实现参考右旋即可。
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;subR->_left = parent;parent->_right = subRL;Node* ppnode = parent->_parent; // 记录parent的父结点parent->_parent = subR;if (subRL){subRL->_parent = parent;}if (ppnode == nullptr){_root = subR;_root->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}parent->_bf = subR->_bf = 0;
}
2.2.3 新节点插入较高左子树的右侧(LR平衡旋转)
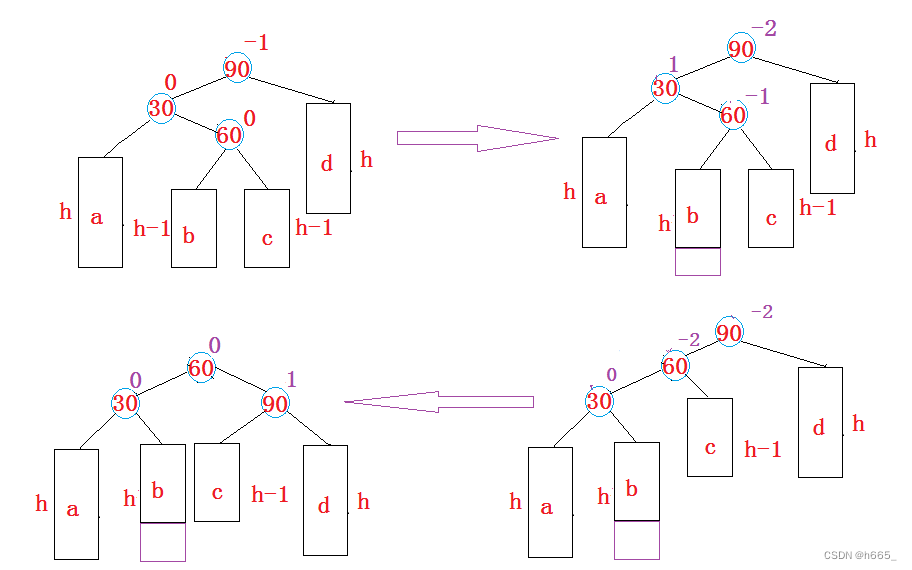
将双旋变成单旋后再旋转,即:先对30进行左单旋,然后再对90进行右单旋,旋转完成后再考虑平衡因子的更新。
void RotateLR(Node* parent)
{// subL:parent的左孩子// subLR:parent的左孩子的右孩子,注意:该点可能不存在Node* subL = parent->_left;Node* subLR = subL->_right;// 旋转之前,保存pSubLR的平衡因子,旋转完成之后,需要根据该平衡因子来调整其他节点的平衡因子int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (1 == bf){subL->_bf = -1;}else if (-1 == bf){parent->_bf = 1;}
}
2.2.4 新节点插入较高右子树的左侧(RL平衡旋转)
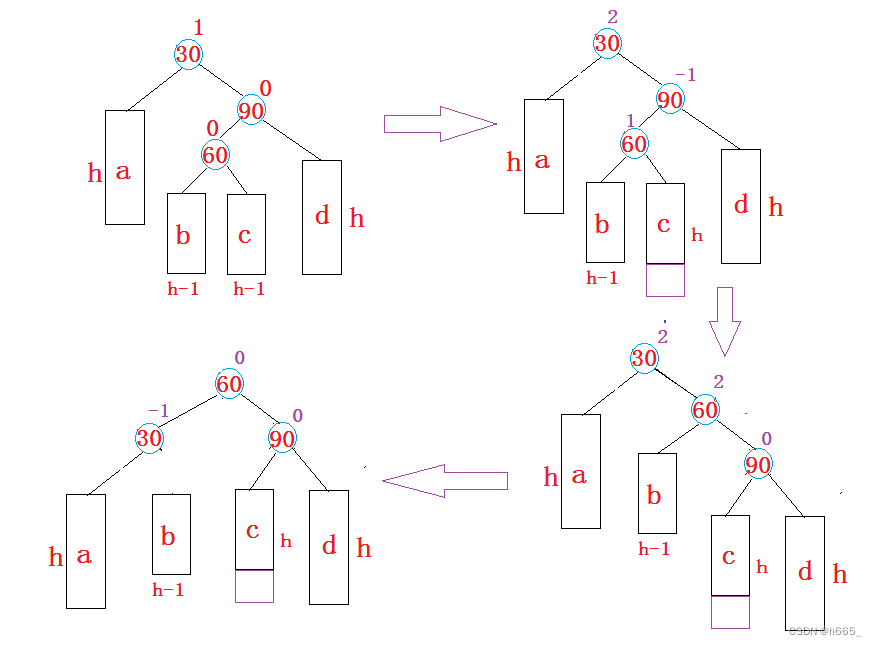
参考右左双旋。
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (1 == bf){parent->_bf = -1;}else if (-1 == bf){subR->_bf = 1;}
}
2.2.5 总结
假如以parent为根的子树不平衡,即parent的平衡因子为2或者-2,分以下情况考虑:
- parent的平衡因子为2,说明parent的右子树高,设parent的右子树的根为subR
当subR的平衡因子为1时,执行左单旋
当subR的平衡因子为-1时,执行右左双旋 - parent的平衡因子为-2,说明parent的左子树高,设parent的左子树的根为subL
当subL的平衡因子为-1是,执行右单旋
当subL的平衡因子为1时,执行左右双旋
旋转完成后,原parent为根的子树个高度降低,已经平衡,不需要再向上更新。
3 平衡二叉树的删除(了解即可)
因为AVL树也是二叉排序树,可按照二叉排序树的方式将节点删除,然后再更新平衡因子,只不错与删除不同的时,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
平衡二叉树删除操作的具体步骤:
- 先按照二叉排序树的方式删除结点
- 一路向上找到最小不平衡子树,找不到就结束
- 找最小不平衡子树下,最高的儿子和孙子
- 根据孙子的位置,调整平衡
- 孙子在LL:右单旋
- 孙子在RR:左单旋
- 孙子在LR:先左旋再右旋
- 孙子再RL:先右旋再左旋
- 如果不平衡向上传导,继续第二步
- 对最小不平衡子树的旋转可能导致树变矮,从而导致上层祖先不平衡
4 平衡二叉树的验证
AVL树是在二叉搜索树的基础上加入了平衡性的限制,因此要验证AVL树,可以分两步:
- 验证其为二叉搜索树
如果中序遍历可得到一个有序的序列,就说明为二叉搜索树 - 验证其为平衡树
- 每个节点子树高度差的绝对值不超过1(注意节点中如果没有平衡因子)
- 节点的平衡因子是否计算正确
// 求二叉树的高度
int _Height(Node* root)
{if (root == nullptr){return 0;}int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;
}
// 验证平衡树
bool _Isbalance(Node* root)
{if (root == nullptr){return true;}int leftH = _Height(root->_left);int rightH = _Height(root->_right);if (rightH - leftH != root->_bf){cout << root->_kv.first << "结点平衡因子异常" << endl;return false;}return rightH - leftH < 2&& _Isbalance(root->_left)&& _Isbalance(root->_right);
}
三、平衡二叉树的效率分析
在平衡二叉树上进行查找的过程与二叉排序树相同。因此,在查找过程中,进行关键字的比较次数不超过树的深度。假设以 n h n_h nh表示深度为h的平衡二叉树中含有的最少结点数。 n 0 = 0 , n 1 = 1 , n 2 = 2 n_0=0,n_1=1,n_2=2 n0=0,n1=1,n2=2,并且有 n h = n h − 2 + n h − 1 + 1 n_h=n_{h-2}+n_{h-1}+1 nh=nh−2+nh−1+1含有n个结点的平衡二叉树的最大深度为 O ( l o g 2 n ) O(log_2n) O(log2n),因此平均查找效率为 O ( l o g 2 n ) O(log_2n) O(log2n)。
但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
相关文章:

【C++】平衡二叉树(AVL树)的实现
目录 一、AVL树的概念二、AVL树的实现1、AVL树的定义2. 平衡二叉树的插入2.1 按照二叉排序树的方式插入并更新平衡因子2.2 AVL树的旋转2.2.1 新节点插入较高左子树的左侧(LL平衡旋转)2.2.2 新节点插入较高右子树的右侧(RR平衡旋转)…...

第一百一十八节 Java面向对象设计 - Java接口
Java面向对象设计 - Java接口 什么是接口? Java中的接口定义了一个引用类型来创建抽象概念。接口由类实现以提供概念的实现。 在Java 8之前,一个接口只能包含抽象方法。 Java 8允许接口具有实现的静态和默认方法。 接口通过抽象概念定义不相关类之间…...

Flink nc -l -p 监听端口测试
1、9999端口未占用 netstat -apn|grep 99992、消息发送端 nc -l -k -p 9999 {"user":"ming","url":"www.baidu1.com", "timestamp":1200L, "score":1} {"user":"xiaohu","url":…...

在IntelliJ IDEA中使用Spring Boot:快速配置
使用IntelliJ IDEA开发Spring Boot应用程序可以极大地提高开发效率,因为IDEA提供了许多便捷的功能,比如自动补全、代码分析、热部署等。以下是一篇可能的CSDN博客文章草稿,介绍如何在IntelliJ IDEA中使用Spring Boot: 在IntelliJ …...

django filter 批量修改
django filter 批量修改 在Django中,如果你想要批量修改记录,可以使用update()方法。这个方法允许你在一个查询集上执行批量更新,而不需要为每条记录生成单独的数据库事务。 以下是一个使用update()方法批量修改记录的例子: fro…...
maven:中央仓库验证方式改变:401 Content access is protected by token
前几天向maven中央仓库发布版本,执行上传命令mvn release:perform时报错了: [ERROR] Failed to execute goal org.sonatype.plugins:nexus-staging-maven-plugin:1.6.13:deploy (injected-nexus-deploy) on project xxxxx: Failed to deploy artifacts: …...

【面试】http
一、定义 HTTP(超文本传输协议),是一种用于分布式、协作式、超媒体信息系统的应用层协议,它是万维网数据通信的基础。主要特点是无状态(服务器不会保存之前请求的状态)、无连接(服务器处理完请…...

获取泛型,泛型擦除,TypeReference 原理分析
说明 author blog.jellyfishmix.com / JellyfishMIX - githubLICENSE GPL-2.0 获取泛型,泛型擦除 下图中示例代码是一个工具类用于生成 csv 文件,需要拿到数据的类型,使用反射感知数据类型的字段,来填充表字段名。可以看到泛型…...

springboot 3.x 之 集成rabbitmq实现动态发送消息给不同的队列
背景 实际项目中遇到针对不同类型的消息,发送消息到不同的队列,而且队列可能还不存在,需要动态创建,于是写了如下代码,实践发现没啥问题,这里分享下。 环境 springboot 3.2 JDK 17 rabbitMQ模型介绍 图片…...

C++ 代码实现鼠标右键注册菜单,一级目录和二级目录方法
最近做的一个项目, 在使用windows的时候,我希望在右键菜单中添加一个自定义的选项, 该选项下有我经常使用的多个程序快捷方式, 直接上代码 头文件 #pragma once #include <Windows.h> #include <iostream> #include <string> using namespace std; …...

SQLite 3 优化批量数据存储操作---事务transaction机制
0、事务操作 事务的目的是为了保证数据的一致性和完整性。 事务(Transaction)具有以下四个标准属性,通常根据首字母缩写为 ACID: 原子性(Atomicity):确保工作单位内的所有操作都成功完成&…...

[程序员] 表达的能力
之前看CSDN的问答区,很多时候,感觉问题的描述所要表达的意思非常模糊,或者说描述不清。如果是想回答问题的人想回答问题,首先要搞清楚是什么问题,就需要再问问题主很多细节的东西。三来四去,才能搞清楚具体…...
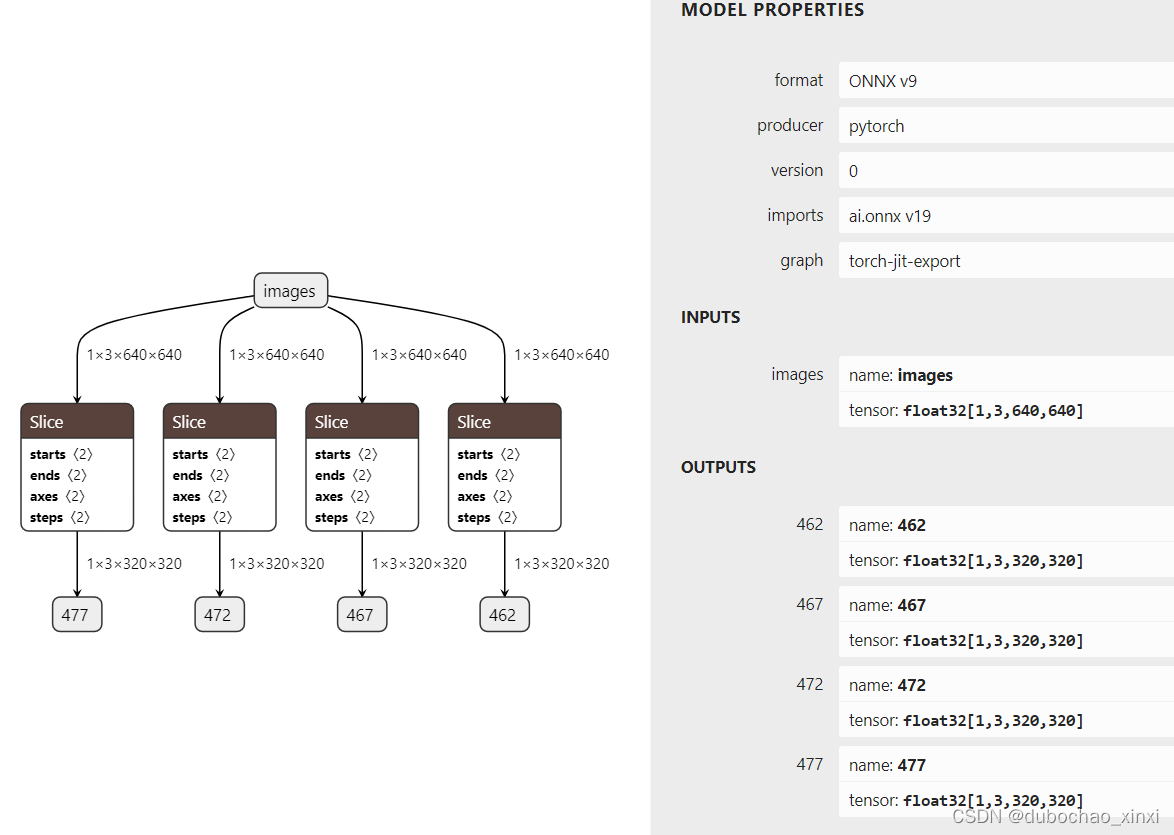
rknn转换后精度差异很大,失真算子自纠
下面是添加了详细注释的优化代码: import cv2 import numpy as np import onnx import onnxruntime as rt from onnx import helper, shape_inferencedef get_all_node_names(model):"""获取模型中所有节点的名称。参数:model (onnx.ModelProto): O…...

【C语言】解决C语言报错:Stack Overflow
文章目录 简介什么是Stack OverflowStack Overflow的常见原因如何检测和调试Stack Overflow解决Stack Overflow的最佳实践详细实例解析示例1:递归调用过深示例2:分配过大的局部变量示例3:嵌套函数调用过多 进一步阅读和参考资料总结 简介 St…...

【滚动哈希 二分查找】1044. 最长重复子串
本文涉及知识点 滚动哈希 二分查找算法合集 LeetCode 1044. 最长重复子串 给你一个字符串 s ,考虑其所有 重复子串 :即 s 的(连续)子串,在 s 中出现 2 次或更多次。这些出现之间可能存在重叠。 返回 任意一个 可能具…...

webid、sec_poison_id、a1、web_session参数分析与算法实现
文章目录 1. 写在前面2. 参数分析3. 核心算法【🏠作者主页】:吴秋霖 【💼作者介绍】:擅长爬虫与JS加密逆向分析!Python领域优质创作者、CSDN博客专家、阿里云博客专家、华为云享专家。一路走来长期坚守并致力于Python与爬虫领域研究与开发工作! 【🌟作者推荐】:对爬…...

Qt|QWebSocket与Web进行通讯,实时接收语音流
实现功能主要思路:在网页端进行语音输入,PC机可以实时接收并播放语音流。 此时,Qt程序做客户端,Web端做服务器,使用QWebSocket进行通讯,实时播放接收的语音流。 功能实现 想要实现该功能,需要…...

「51媒体」电视台媒体邀约采访报道怎么做?
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 电视台作为地方主流媒体,对于新闻报道有着严格的选题标准和报道流程。如果您希望电视台对某个会议或活动进行报道,可以按这样的方法来做: 1.明确活动信…...

Python提取PDF文本和图片,以及提前PDF页面中指定矩形区域的文本
前言 从PDF中提取内容能帮助我们获取文件中的信息,以便进行进一步的分析和处理。此外,在遇到类似项目时,提取出来的文本或图片也能再次利用。要在Python中通过代码提取PDF文件中的文本和图片,可以使用 Spire.PDF for Python 这个…...

C#实现边缘锐化(图像处理)
在 C# 中进行图像的边缘锐化,可以通过卷积滤波器实现。边缘锐化的基本思想是通过卷积核(也称为滤波器或掩模)来增强图像中的边缘。我们可以使用一个简单的锐化核,例如: [ 0, -1, 0][-1, 5, -1][ 0, -1, 0]这个卷积核…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
