一个C#开发的开源的快速启动工具
更多开源项目请查看:一个专注推荐.Net开源项目的榜单
平常计算机安装软件比较多、或者工作涉及的文件比较多,很多人都会直接放在桌面,一方面不安全,还不容易查找,这时候我们往往,都会放在其他硬盘内,每一次都有多次点击才能定位到文件。今天给大家推荐一款工具,让可以让我们快速定位和查找文件、软件。
项目简介
这是基于.Net 6开发的、开源工具,它可以让我们快速定位文件、软件,并直接打开,可以提升我们的工作效率,节省查找文件的时间。
它默认打开我们指定的根目录文件夹,在这个文件夹内,我们可以放入一些常用文件、软件快捷方式、网页快捷方式、资源等等。
工具主要功能
1、可以设定根目录,工具启动时,默认展示根目录的文件,并支持搜索;
2、支持快捷键操作工具打开、关闭、选择文件等操作;
3、支持设定中英文等全球各种语言;
4、支持个性化定制菜单的大小和位置;
5、定制软件的皮肤。
技术架构
1、跨平台:基于.Net 6开发,支持Windows。
项目结构
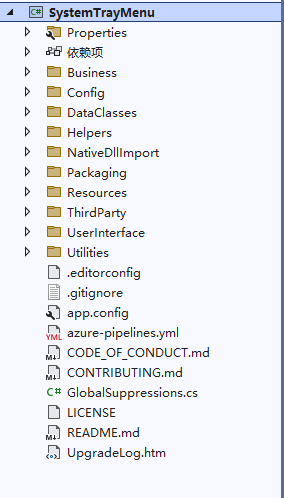
工具部分功能截图
第一次启动,设置根目录
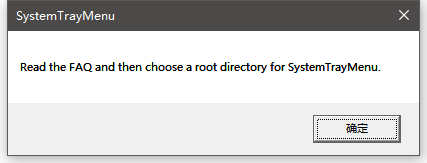
文件夹列表并支持多级搜索
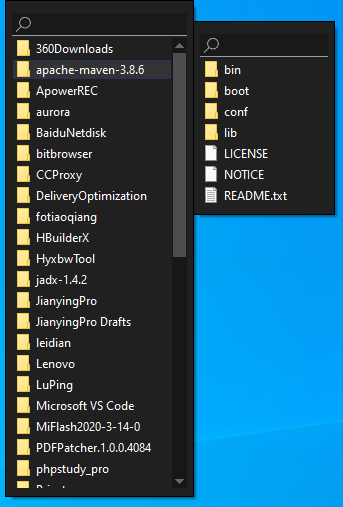
目录、快捷键、语言等设置
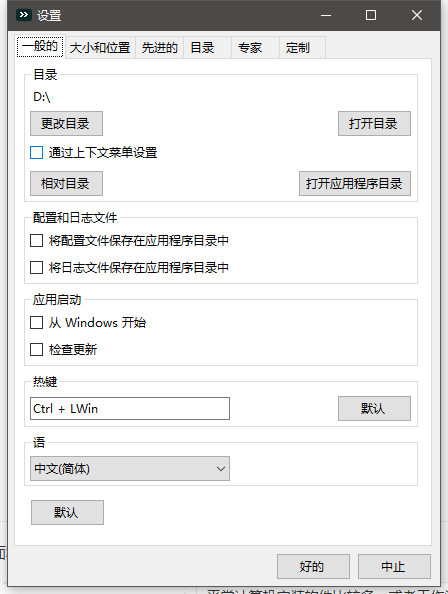
工具大小、位置等设置
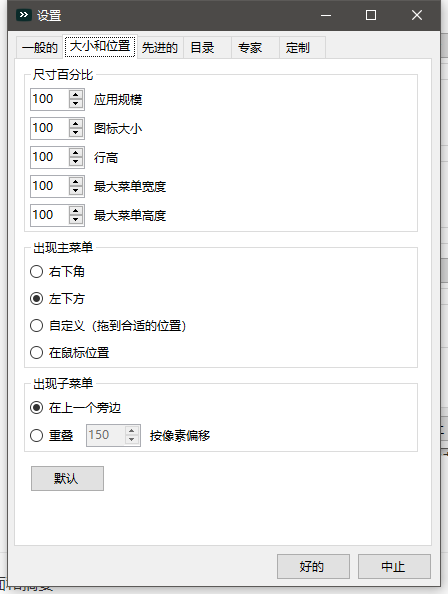
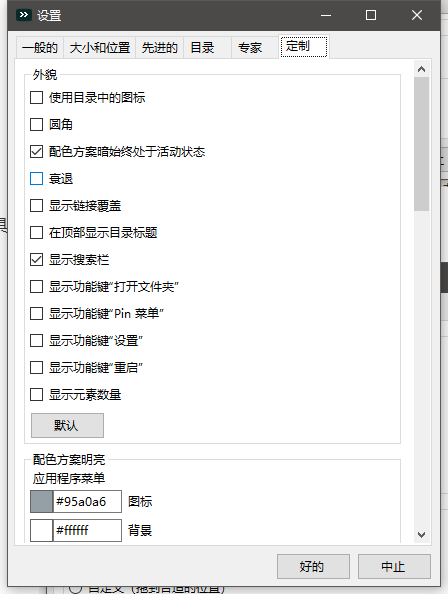
定制皮肤
项目地址
https://github.com/Hofknecht/SystemTrayMenu
- End -
推荐阅读
一个.Net Core开源缓存中间件,让你更加简单、方便使用缓存
一个.Net Core开源监控解决方案,支持Redis、Elasticsearch、SqlServer
盘点3个.Net开发的WMS仓库管理系统
推荐一个前后端分离.NetCore+Angular快速开发框架
一个可视化动画算法网站,值得收藏!
相关文章:

一个C#开发的开源的快速启动工具
更多开源项目请查看:一个专注推荐.Net开源项目的榜单 平常计算机安装软件比较多、或者工作涉及的文件比较多,很多人都会直接放在桌面,一方面不安全,还不容易查找,这时候我们往往,都会放在其他硬盘内&#x…...
Paddle项目调试记录
PaddlePaddle是百度公司提出的深度学习框架。近年来深度学习在很多机器学习领域都有着非常出色的表现,在图像识别、语音识别、自然语言处理、机器人、网络广告投放、医学自动诊断和金融等领域有着广泛应用。面对繁多的应用场景,深度学习框架有助于建模者…...

3月11日,30秒知全网,精选7个热点
///微盟集团宣布接入百度文心一言 据介绍,微盟SaaS产品和数字营销服务将与文心一言的技术能力实现深度融合,通过AIGC技术,深化微盟在营销AI创意内容生产、智能营销、智能客服、智能经营等方面的布局 ///T3出行与华为云深化业务合作 双方将在…...
)
C win32基础学习(四)
上一篇我们已经介绍了关于窗口处理函数的知识。本篇我们说一下注册窗口类,创建窗口和显示窗口的内容。 前文 窗口创建过程 定义WinMain函数 定义窗口处理函数(自定义,处理消息) 注册窗口类(向操作系统写入一些数据) 创建窗口&…...
)
Java 日期时间API(Java 8及以上)
Java 8及以上版本提供了新的日期时间API,其中包括了LocalDate、LocalTime、LocalDateTime、ZonedDateTime、Duration、Period等类,这些类提供了更加丰富和灵活的日期时间操作方法。 LocalDate LocalDate类表示一个本地日期,不包含时间和时区…...

DHCP的配置
实验目的熟悉DHCP的应用场景掌握DHCP的配置方法实验拓扑DHCP的配置如图15-2所示: 图15-2:DHCP的配置 实验步骤配置IP地址<Huawei>system-view Enter system view, return user view with Ctrl+Z....
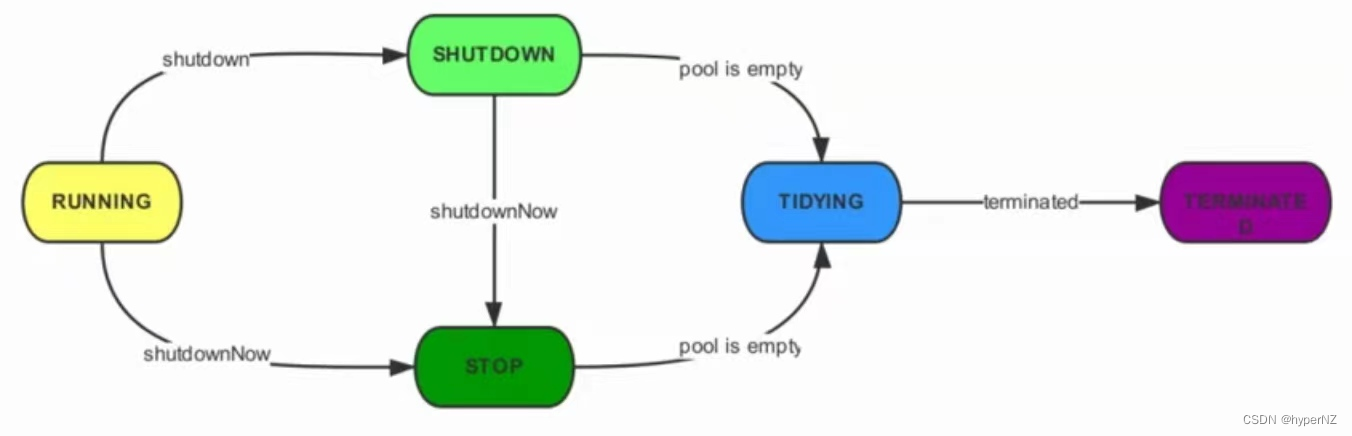
JavaWeb14-线程池
目录 1.传统线程的缺点 2.线程池的定义 3.线程池的优点 4.线程池的创建/使用(2类7种) 4.1.通过Executors(执行器)自动创建(6种) ①Executors.newFixedThreadPool:创建⼀个固定⼤⼩的线程池…...

[qiankun+nuxt]子应用请求本地文件报错404
前言 目前公司的前端架构是qiankunnuxt做的微前端项目 问题说明 在子应用中,前端需要模拟一些数据,方便后期演示调整而不需要重新打包 所以将一些数据存储到了本地的json文件中,但是获取时报了404的错误,找不到该文件。 页面报错…...
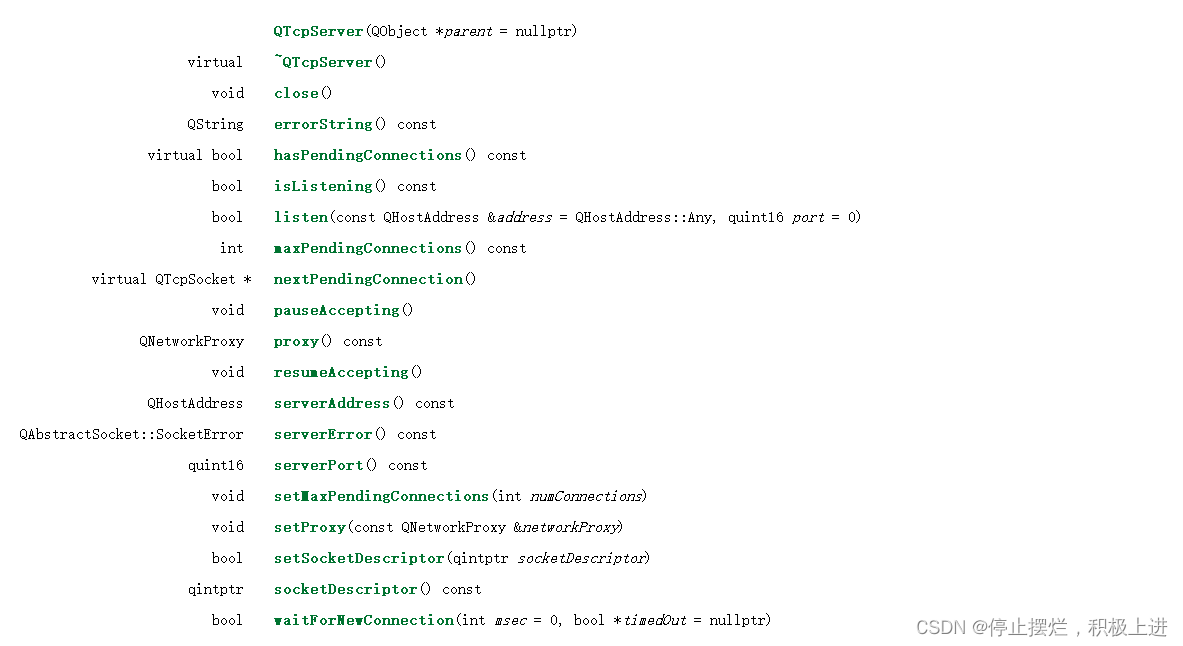
【Qt网络编程】实现TCP协议通信
文章目录概要:本期主要讲解QT中对于TCP协议通信的实现。一、TCP协议二、Qt中TCP协议处理1.QTcpSocket2.QTcpServer三、Qt实现TCP通信1.客户端2.服务器端结尾概要:本期主要讲解QT中对于TCP协议通信的实现。 一、TCP协议 传输控制协议(TCP&am…...

Webpack打包———处理样式资源
基本使用 本质上,webpack 是一个用于现代 JavaScript 应用程序的 静态模块打包工具。当 webpack 处理应用程序时,它会在内部从一个或多个入口点构建一个 依赖图(dependency graph),然后将你项目中所需的每一个模块组合成一个或多个 bundles&a…...
 A~D)
VP记录:Codeforces Round 857 (Div. 2) A~D
传送门:CF A题 Likes: 这道题的题意很变态,十分的难懂,简直就是一坨shit,这场比赛最后被骂是有原因的 简单来说就是对于一个项目,每一个人都能对此加一或者减一,最后问你这个项目每一时刻最大和最小是多少.题目中只说明了只能点赞后才能取消,并没有解释存在取消操作必存在点…...
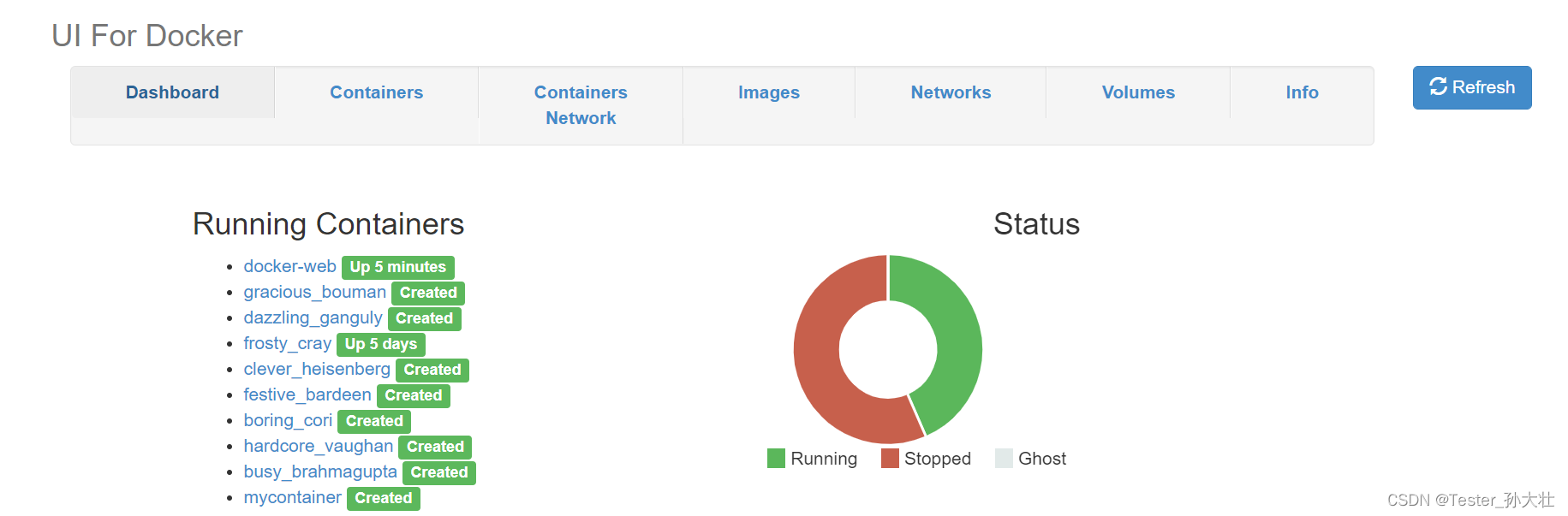
Docker常用项目实战演练
docker镜像源的修改 linux环境下编辑 /etc/docker/daemon.json vi /etc/docker/daemon.json #如添加如下网易镜像源 { "registry-mirrors": ["http://hub-mirror.c.163.com"] }docker run命令详细解释 日常工作中用的比较多的是docker run命令ÿ…...

Linux进程间通信-FIFO命名管道
Linux进程间通信-FIFO命名管道 1、概述 管道因为没有名称,所以只用于进程间的亲缘通信。为了克服这一缺点,提出了命名管道(FIFO),又称命名管道、FIFO文件。 FIFO不同于无名管道,它提供与之关联的路径名,该路径名以FIF…...

【Kafka】记录一次基于connect-mirror-maker做的Kafka集群迁移完整过程
文章目录背景环境工具选型实操MM1MM2以MM2集群运行以Standalone模式运行验证附录MM2配置表其他背景 一个测试环境的kafka集群,Topic有360,Partition有2000,部署在虚拟机上,由于多方面原因,要求迁移至k8s容器内&#x…...

实现VOC数据集与COCO数据集格式转换
实现VOC数据集与COCO数据集格式转换2、将voc数据集的xml转化为coco数据集的json格式2、COCO格式的json文件转化为VOC格式的xml文件3、将 txt 文件转换为 Pascal VOC 的 XML 格式<annotation><folder>文件夹目录</folder><filename>图片名.jpg</file…...

常用的密码算法有哪些?
我们将密码算法分为两大类。 对称密码(密钥密码)——算法只有一个密钥。如果多个参与者都知道该密钥,该密钥 也称为共享密钥。非对称密码(公钥密码)——参与者对密钥的可见性是非对称的。例如,一些参与者仅…...
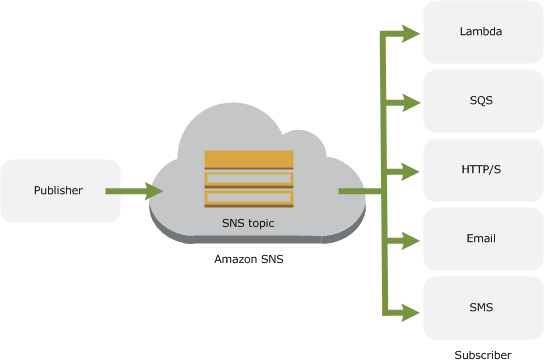
SNS (Simple Notification Service)简介
SNS (Simple Notification Service) 是一种完全托管的发布/订阅消息收发和移动通知服务,用于协调向订阅终端节点和客户端的消息分发。 和SQS (Simple Queue Service)一样,SNS也可以轻松分离和扩展微服务,分布式系统和无服务应用程序…...

JVM初步理解浅析
一、JVM的位置 JVM的位置 JVM在操作系统的上一层,是运行在操作系统上的。JRE是运行环境,而JVM是包含在JRE中 二、JVM体系结构 垃圾回收主要在方法区和堆,所以”JVM调优“大部分也是发生在方法区和堆中 可以说调优就是发生在堆中…...

【巨人的肩膀】MySQL面试总结(一)
💪 目录💪1、什么是ER图2、数据库范式了解吗3、超键、候选键、主键、外键分别是什么?4、为什么不推荐使用外键与级联5、什么是存储过程6、drop、delete与truncate区别7、数据库设计通常分为那几步8、什么是关系型数据库9、什么是SQL10、MySQL…...
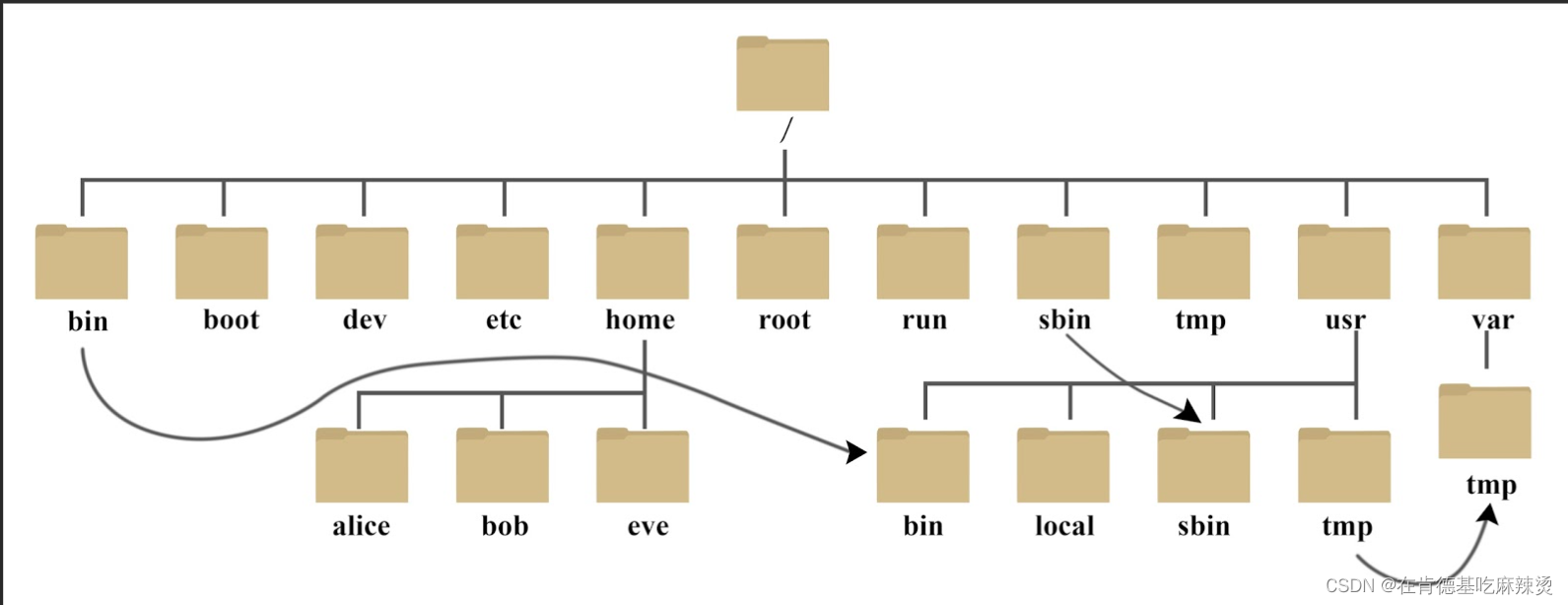
【数据结构之树】——什么是树,树的特点,树的相关概念和表示方法以及在实际的应用。
文章目录一、1.树是什么?2.树的特点二、树的相关概念三、树的表示方法1.常规方法表示树2.使用左孩子右兄弟表示法3. 使用顺序表来存储父亲节点的下标三、树在实际的应用总结一、1.树是什么? 树是一种非线性的数据结构,它是由n(n&…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
