二叉树经典OJ练习
个人主页:C++忠实粉丝
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C++忠实粉丝 原创二叉树经典OJ练习
收录于专栏【数据结构初阶】
本专栏旨在分享学习数据结构学习的一点学习笔记,欢迎大家在评论区交流讨论💌
目录
前置说明
1. 单值二叉树
2. 相同的树
3. 对称二叉树
4. 二叉树的前序遍历
5. 二叉树中序遍历
6. 二叉树的后序遍历
7. 另一颗树的子树
前置说明
这里大家需要有二叉树的一些基础,还不是很了解的宝子们可以点击下方链接进行查看
---数据结构之二叉树的超详细讲解(3)--(二叉树的遍历和操作)-CSDN博客
1. 单值二叉树
Oj链接--965. 单值二叉树 - 力扣(LeetCode)
题目描述:
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。
示例 1:
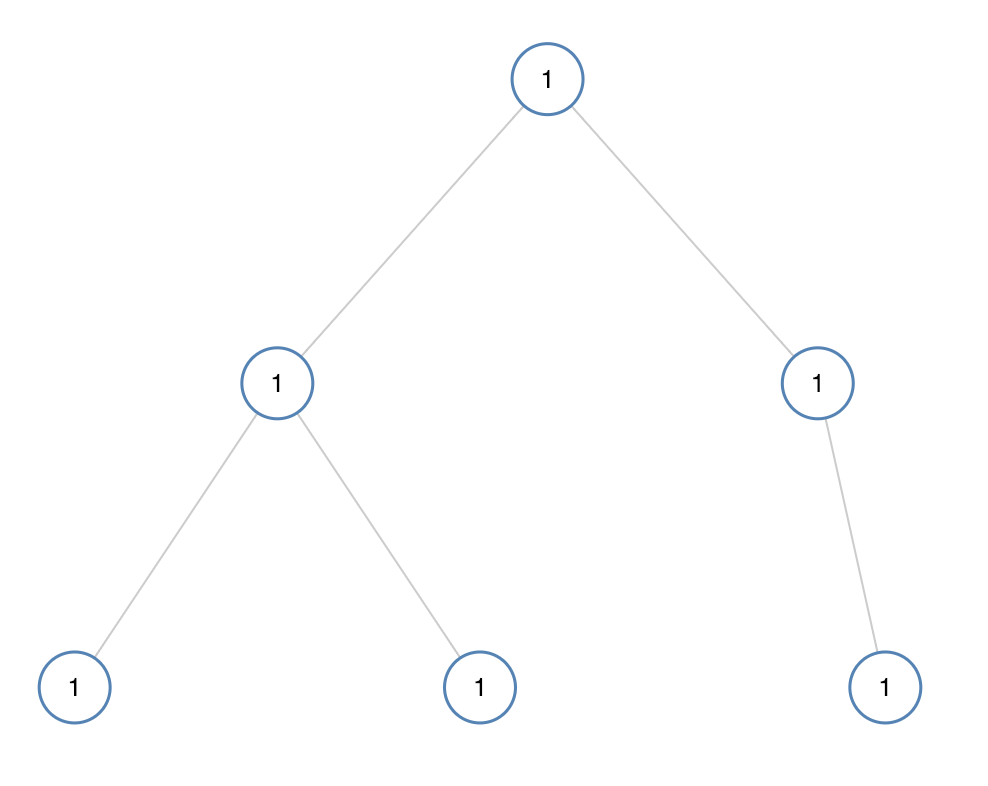
输入:[1,1,1,1,1,null,1] 输出:true
示例 2:
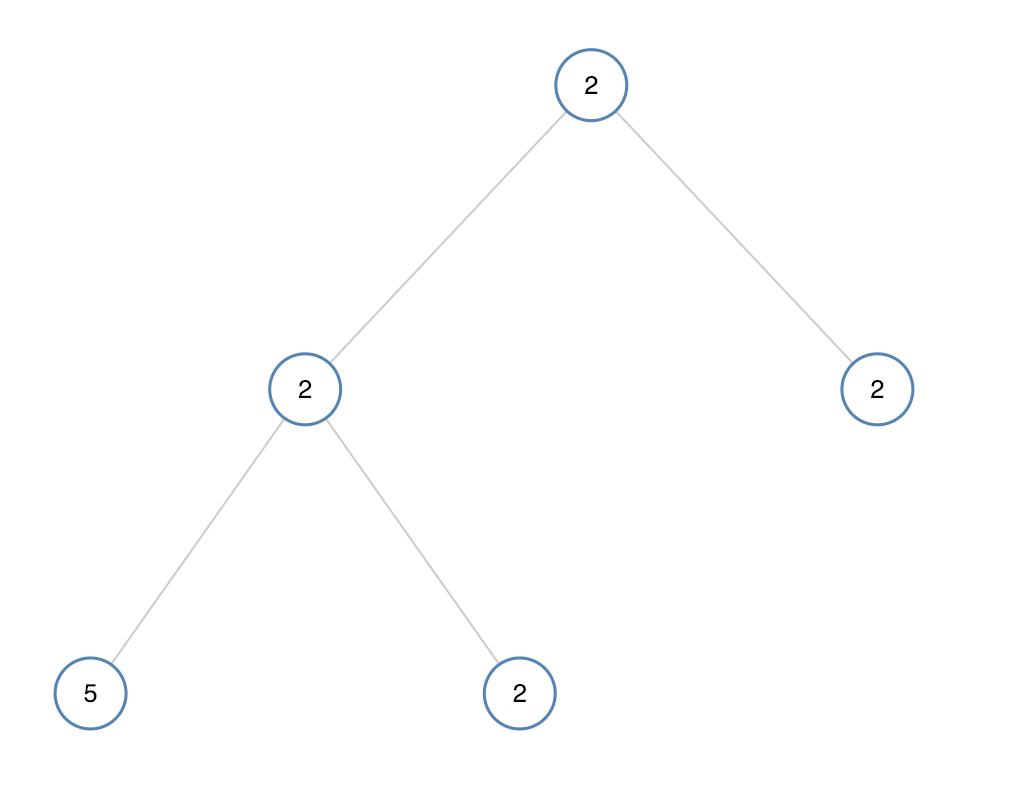
输入:[2,2,2,5,2] 输出:false
提示:
- 给定树的节点数范围是
[1, 100]。 - 每个节点的值都是整数,范围为
[0, 99]。
分析:
题目中给定树的节点数范围是
[1, 100],这里我们就不需要额外判断空节点的情况,我们只需要对二叉树进行遍历一遍,如果遇到空节点返回true,如果root左节点或右节点val不等于root->val,返回false,将最后的结果上传,即可得到最终的结果.
代码展示:
bool isUnivalTree(struct TreeNode* root) {if(root == NULL)return true;if(root->left && root->left->val != root->val)return false;if(root->right && root->right->val != root->val)return false;return isUnivalTree(root->left) && isUnivalTree(root->right);
}核心逻辑
空树检查
if(root == NULL) return true;这里首先检查根节点是否为空。如果根节点为空,则该树被认为是单值二叉树,返回
true。左子节点值检查
if(root->left && root->left->val != root->val) return false;接下来检查左子节点。如果左子节点存在且其值与根节点的值不相同,则该树不是单值二叉树,返回
false。右子节点值检查
if(root->right && root->right->val != root->val) return false;同样地,检查右子节点。如果右子节点存在且其值与根节点的值不相同,则该树不是单值二叉树,返回
false。递归检查子树
return isUnivalTree(root->left) && isUnivalTree(root->right);如果当前节点及其直接子节点都满足条件,则递归检查左子树和右子树。只有在左右子树都是单值二叉树的情况下,当前树才是单值二叉树。
总结
该函数通过递归检查每个节点及其子节点的值是否与根节点的值相同来判断整个二叉树是否是单值二叉树。如果某个节点的值与其父节点不同,立即返回
false。否则,继续递归检查其子树,最终返回整个树的结果。
2. 相同的树
OJ链接--100. 相同的树 - 力扣(LeetCode)
题目描述:
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
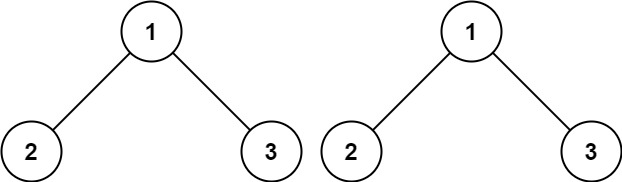
输入:p = [1,2,3], q = [1,2,3] 输出:true
示例 2:
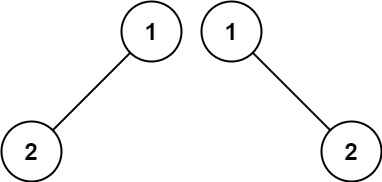
输入:p = [1,2], q = [1,null,2] 输出:false
示例 3:
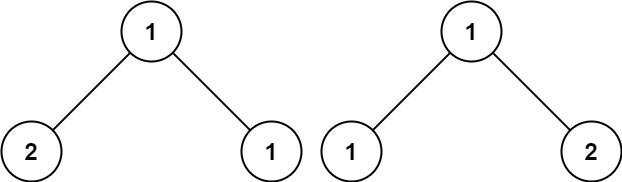
输入:p = [1,2,1], q = [1,1,2] 输出:false
提示:
- 两棵树上的节点数目都在范围
[0, 100]内 -104 <= Node.val <= 104
分析:
两棵树上的节点数目都在范围
[0, 100]内,说明这里需要进行空树的判断,我们需要先进行判断,当两棵树节点都为空时,满足条件,返回true.当两个节点只有一个为空时,不满足条件,返回false.当两个节点都不为空时,比较两个节点的val,不相等返回false.然后递归遍历两棵树.
代码展示:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if(p == NULL && q == NULL)return true;if(p == NULL || q == NULL)return false;if(p->val != q->val)return false;return isSameTree(p->left , q->left) && isSameTree(p->right, q->right);
}
- 首先检查
p和q是否同时为NULL,如果是,说明两棵树都为空,返回true。- 然后检查
p和q是否其中一个为NULL,另一个不是。如果是,说明两棵树中的节点个数不同,返回false。- 接着检查
p和q的当前节点值是否相同,如果不同,返回false。- 最后,通过递归调用
isSameTree函数比较两棵树的左子树和右子树是否相同,如果均相同则返回true,否则返回false。这段代码非常简洁而且有效地比较了两棵树是否相同。它利用了递归的特性,逐层比较树的节点值以及对应的子树,从而判断两棵树是否相同。
3. 对称二叉树
OJ链接--101. 对称二叉树 - 力扣(LeetCode)
题目描述:
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
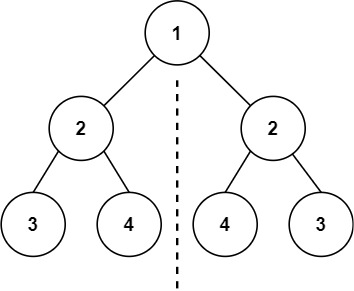
输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:
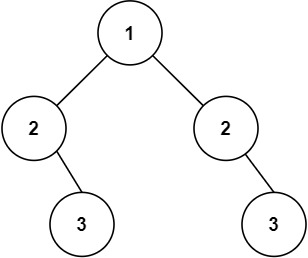
输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
代码展示:
bool check(struct TreeNode* p, struct TreeNode* q)
{if(p == NULL && q == NULL)return true;if(p == NULL || q == NULL)return false;if(p->val == q->val)return check(p->left, q->right) && check(p->right, q->left);elsereturn false;
}bool isSymmetric(struct TreeNode* root) {return check(root, root);
}分析:
check函数:
- 首先检查
p和q是否同时为NULL,如果是,说明两个节点都为空,返回true。- 然后检查
p和q是否其中一个为NULL,另一个不是。如果是,说明两个节点中的一个为空,另一个不为空,返回false。- 接着检查
p和q的值是否相等,如果相等,则递归地比较p的左子树和q的右子树,以及p的右子树和q的左子树是否对称。如果均对称,则返回true,否则返回false。
isSymmetric函数:
- 调用
check函数,并传入根节点的左右子树作为参数进行比较。这段代码利用递归的方式判断了一棵二叉树是否对称。它通过比较树的左右子树是否镜像对称来判断整棵树是否对称。整体上,这段代码实现了一个简洁而有效的对称性判断算法。
函数递归展开图:
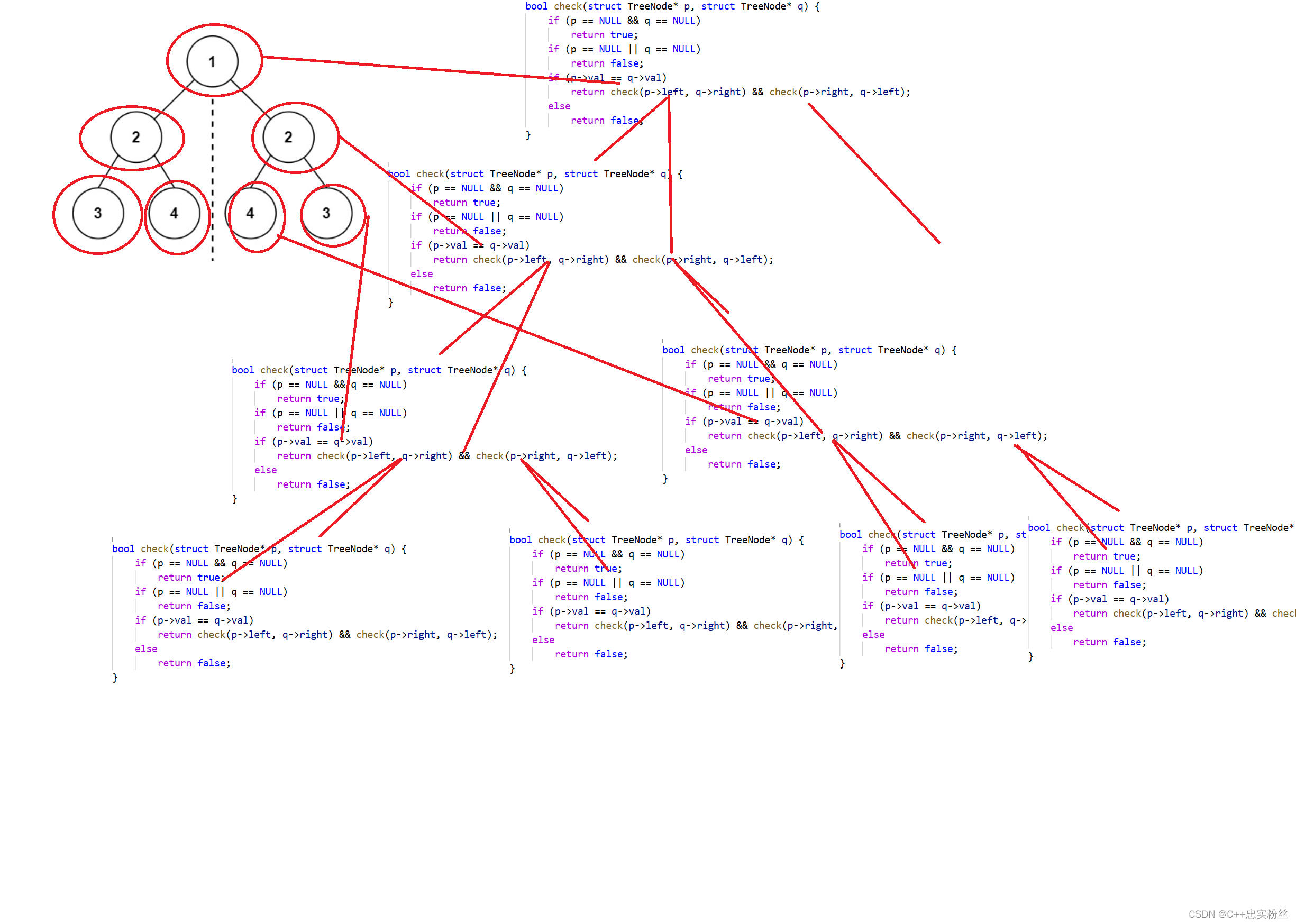
4. 二叉树的前序遍历
OJ链接--144. 二叉树的前序遍历 - 力扣(LeetCode)
题目描述:
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
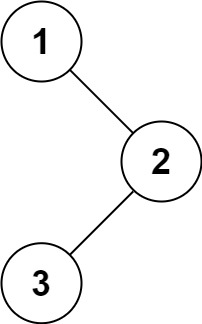
输入:root = [1,null,2,3] 输出:[1,2,3]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
示例 4:
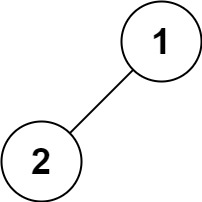
输入:root = [1,2] 输出:[1,2]
示例 5:
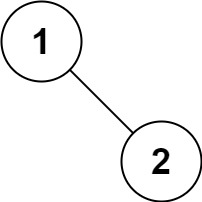
输入:root = [1,null,2] 输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
分析:
注意这道题目的要求:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* preorderTraversal(struct TreeNode* root, int* returnSize) {}
这里我们需要返回的是前序遍历好的数组,而且需要我们自己malloc创建.函数的参数一个是根节点一个是节点个数,要我们实现的是一个输出型函数.
代码展示:
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}void preOrder(struct TreeNode* root, int* a, int* pi)
{if(root == NULL)return;a[(*pi)++] = root->val;preOrder(root->left, a, pi);preOrder(root->right, a, pi);
}int* preorderTraversal(struct TreeNode* root, int* returnSize) {*returnSize = TreeSize(root);int* a = (int*)malloc(sizeof(int)*(*returnSize));int i = 0;preOrder(root, a, &i);return a;
}这段代码是关于二叉树前序遍历的实现,其中包括了计算二叉树节点总数和返回前序遍历结果的功能。让我们对这段代码进行详细分析:
int TreeSize(struct TreeNode* root) { return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1; }这部分代码是计算二叉树节点总数的函数
TreeSize,使用了递归的方式来统计节点数量。在每个节点上,它会递归地调用自身来计算左子树和右子树的节点数,并加上当前节点。void preOrder(struct TreeNode* root, int* a, int* pi) { if(root == NULL) return; a[(*pi)++] = root->val; preOrder(root->left, a, pi); preOrder(root->right, a, pi); }这部分代码是实现前序遍历的函数
preOrder,它将遍历得到的节点值存储在数组a中,使用指针pi来跟踪数组的索引位置。int* preorderTraversal(struct TreeNode* root, int* returnSize) { *returnSize = TreeSize(root); int* a = (int*)malloc(sizeof(int)*(*returnSize)); int i = 0; preOrder(root, a, &i); return a; }最后,
preorderTraversal函数整合了前两部分的功能。它先计算二叉树的节点总数,然后动态分配一个数组a来存储前序遍历的结果,并调用preOrder函数来填充数组。最终将数组返回。总结
这段代码实现了计算二叉树节点总数并返回其前序遍历结果的功能。通过递归的方式遍历二叉树,将节点值按前序遍历顺序存储在数组中,并返回该数组。这样的实现使得我们能够方便地获取二叉树的前序遍历结果,并且能够有效地处理动态分配内存以存储结果。
5. 二叉树中序遍历
OJ链接--94. 二叉树的中序遍历 - 力扣(LeetCode)
题目描述:
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:

输入:root = [1,null,2,3] 输出:[1,3,2]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
后面的中序和后序跟前序相差不大,这里就不过多解释.
代码展示:
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}void inOrder(struct TreeNode* root, int* a, int* pi)
{if(root == NULL){return;}inOrder(root->left,a,pi);a[(*pi)++] = root->val;inOrder(root->right,a,pi);
}int* inorderTraversal(struct TreeNode* root, int* returnSize) {*returnSize = TreeSize(root);int* a = (int*)malloc(sizeof(int)*(*returnSize));int i = 0;inOrder(root,a,&i);return a;
}6. 二叉树的后序遍历
OJ链接--145. 二叉树的后序遍历 - 力扣(LeetCode)
题目描述:
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
示例 1:
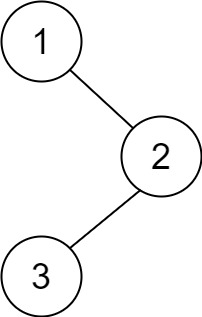
输入:root = [1,null,2,3] 输出:[3,2,1]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
提示:
- 树中节点的数目在范围
[0, 100]内 -100 <= Node.val <= 100
代码展示:
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}void postOrder(struct TreeNode* root, int* a, int* pi)
{if(root == NULL)return;postOrder(root->left, a, pi);postOrder(root->right, a, pi);a[(*pi)++] = root->val;
}int* postorderTraversal(struct TreeNode* root, int* returnSize) {*returnSize = TreeSize(root);int* a = (int*)malloc(sizeof(int)*(*returnSize));int i = 0;postOrder(root, a, &i);return a;
}7. 另一颗树的子树
OJ链接--572. 另一棵树的子树 - 力扣(LeetCode)
题目描述:
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在,返回 true ;否则,返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
示例 1:
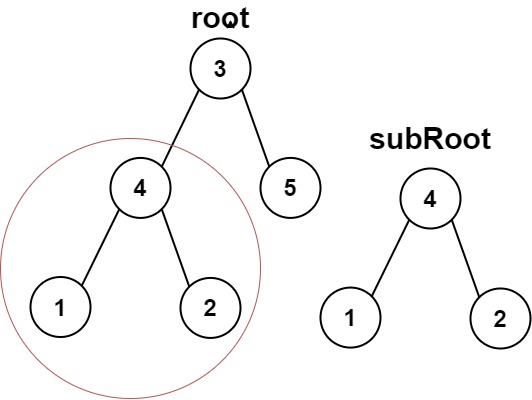
输入:root = [3,4,5,1,2], subRoot = [4,1,2] 输出:true
示例 2:
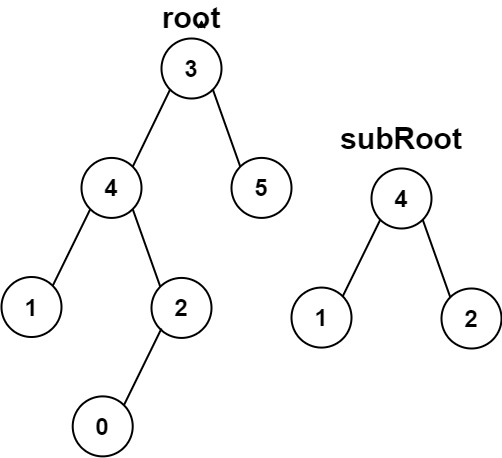
输入:root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] 输出:false
提示:
root树上的节点数量范围是[1, 2000]subRoot树上的节点数量范围是[1, 1000]-104 <= root.val <= 104-104 <= subRoot.val <= 104
分析:
遍历root树,找到root的所有子树与subroot树进行比较
代码展示:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {if(p == NULL && q == NULL)return true;if(p == NULL || q == NULL)return false;if(p->val != q->val)return false;return isSameTree(p->left , q->left) && isSameTree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root == NULL)return false;if(root->val == subRoot->val && isSameTree(root, subRoot))return true;return isSubtree(root->left,subRoot) || isSubtree(root->right, subRoot);
}注意:这里需要用到我们之前已经解决的相同的树的问题
该函数用来判断二叉树
subRoot是否是二叉树root的子树。逻辑解释
空树检查
if(root == NULL) return false;如果
root是空树,直接返回false,因为空树不可能包含任何非空子树。根节点值比较及完整树比较
if(root->val == subRoot->val && isSameTree(root, subRoot)) return true;如果
root的当前节点值与subRoot的根节点值相同,并且root从当前节点开始的子树与subRoot完全相同(通过调用isSameTree函数进行判断),则返回true。递归检查左右子树
return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);如果上述条件都不满足,则递归地检查
root的左子树和右子树,看其中是否存在与subRoot相同的子树。如果任意一个子树包含subRoot,返回true。总结
这两个函数结合起来可以有效地判断一棵二叉树是否是另一棵二叉树的子树。具体步骤如下:
- 使用
isSubtree函数遍历root的每个节点。- 对于每个节点,检查该节点开始的子树是否与
subRoot完全相同。- 如果找到一个与
subRoot相同的子树,立即返回true。- 如果没有找到,继续遍历
root的左右子树,直到所有节点都检查完毕。这种方法通过递归遍历和子树比较,确保准确判断子树关系。
相关文章:

二叉树经典OJ练习
个人主页:C忠实粉丝 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C忠实粉丝 原创 二叉树经典OJ练习 收录于专栏【数据结构初阶】 本专栏旨在分享学习数据结构学习的一点学习笔记,欢迎大家在评论区交流讨论💌 目录 前置说…...

【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】008 - make distclean 命令解析
【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】008 - make distclean 命令解析 一、make V=1 distclean 命令解析系列文章汇总:《【OpenHarmony4.1 之 U-Boot 源码深度解析】000 - 文章链接汇总》 本文链接:《【OpenHarmony4.1 之 U-Boot 2024.07源码深度解析】008 - mak…...
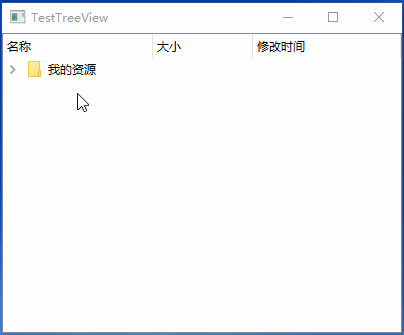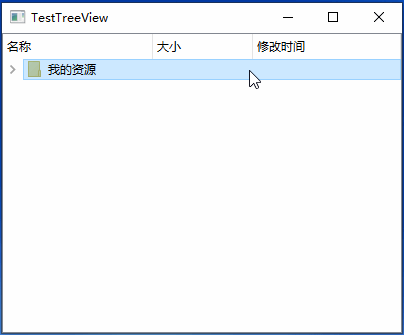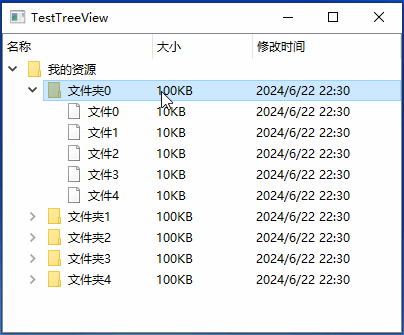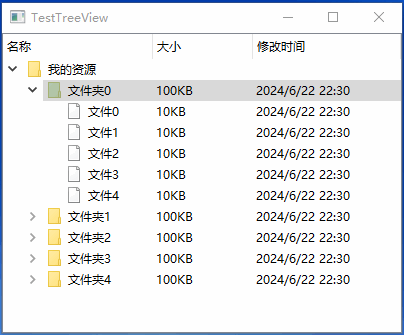
QTreeView双击任意列展开
一.效果 二.原理 重点是如何通过其他列的QModelIndex(假设为index),获取第一列的QModelIndex(假设为firstColumnIndex)。代码如下所示: QModelIndex firstColumnIndex = model->index(index.row(), 0, index.parent()); 这里要注意index函数的第三个参数,第三个参…...
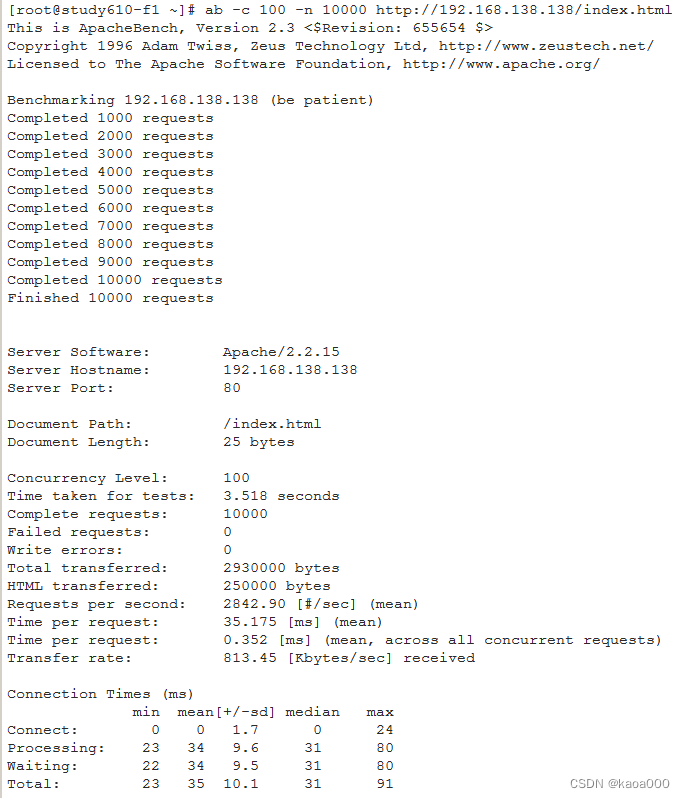
Linux入门攻坚——26、Web Service基础知识与httpd配置-2
http协议 URL:Uniform Resource Locator,统一资源定位符 URL方案:scheme,如http://,https:// 服务器地址:IP:port 资源路径: 示例:http://www.test.com:80/bbs/…...

相由心生与事出反常必有妖
从端午节之日生病起,已就医三次,快半个月了。医检的结论是老病复发—— 上呼吸道感染 。原本并无大碍,加之“水不在深,有龙则灵”的张龙医生处方得当,现已病情好转。只是“800727”趁人之危,兴灾乐祸地欲从…...

微信小程序---支付
一、判断是否登录 如果没有登录,走前端登录流程,不再赘述 二、获取订单编号 跟自己的后端商议入参,然后获取订单编号 三、通过订单编号获取wx.requestPayment()需要的参数 获取订单编号再次请求后端接口,拿到wx.requestPayme…...
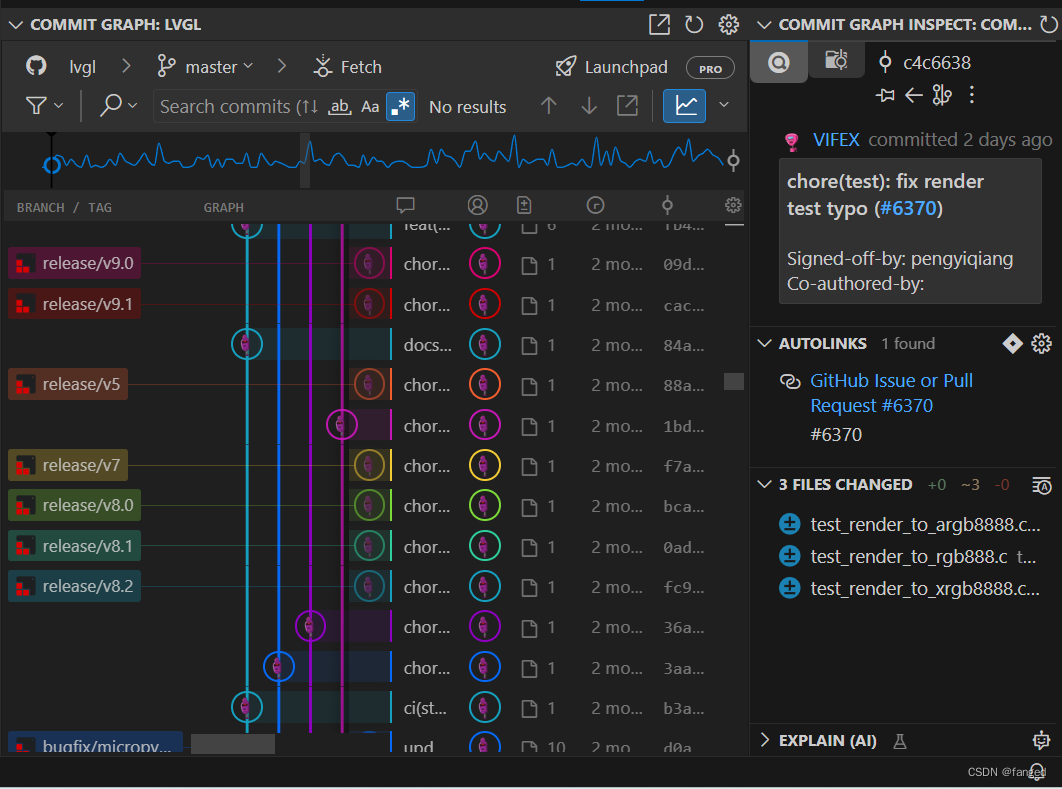
Git学习2 -- VSCode中的Git
看了下,主要的插件有3个。自带的Source Control。第1个是Gitlens,第2个是Git Graph。第三个还有个git history。 首先是Source Control。界面大概是这样的。 还是挺直观的。在第一栏source control,可以进行基本的git操作。主要的git操作都是…...

VC++支持断点续下或续传的功能
VC使用多线程和Socket实现断点续下 一、断点续下的基本原理: 1.断点续传的理解可以分为两部分:一部分是断点,一部分是续传。断点的由来是在下载过程中,将一个下载文件分成了多个部分,同时进行多个部分一起的下载&…...
机器学习数学原理专题——线性分类模型:损失函数推导新视角——交叉熵
目录 二、从回归到线性分类模型:分类 3.分类模型损失函数推导——极大似然估计法 (1)二分类损失函数——极大似然估计 (2)多分类损失函数——极大似然估计 4.模型损失函数推导新视角——交叉熵 (1&#x…...

windows和linux路径斜杆转换脚本,打开即用
前言: windows和linux的目录路径斜杆是相反的,在ssh或者其他什么工具在win和ubuntu传文件时候经常需要用到两边的路径,有这个工具就不用手动去修改斜杆反斜杠了。之前有个在线网站,后来挂了,就想着自己搞一个脚本来用。…...

在Android系统中,查看apk安装路径
在Android系统中,应用通常安装在内部存储的特定目录下。要找到已安装应用的路径,可以通过ADB(Android Debug Bridge)工具来查询。以下是一些步骤和命令,可以帮助你找到应用的安装路径: 使用pm list package…...

管理不到位,活该执行力差?狠抓这4点要素,强化执行力
管理不到位,活该执行力差?狠抓这4点要素,强化执行力 一:强化制度管理 1、权责分明,追责管理 要知道,规章制度其实就是一种“契约”。 在制定制度和规则的时候,民主一点,征求团队成员…...

应届毕业之本科简历制作
因为毕设以及编制岗位面试,最近好久没有更新了,刚好有同学问如何制作简历,我就准备将我自己制作简历的流程分享给各位,到此也算是一个小的结束,拿了工科学位证书毕业去做🐂🐎了。 简历主要包含内…...
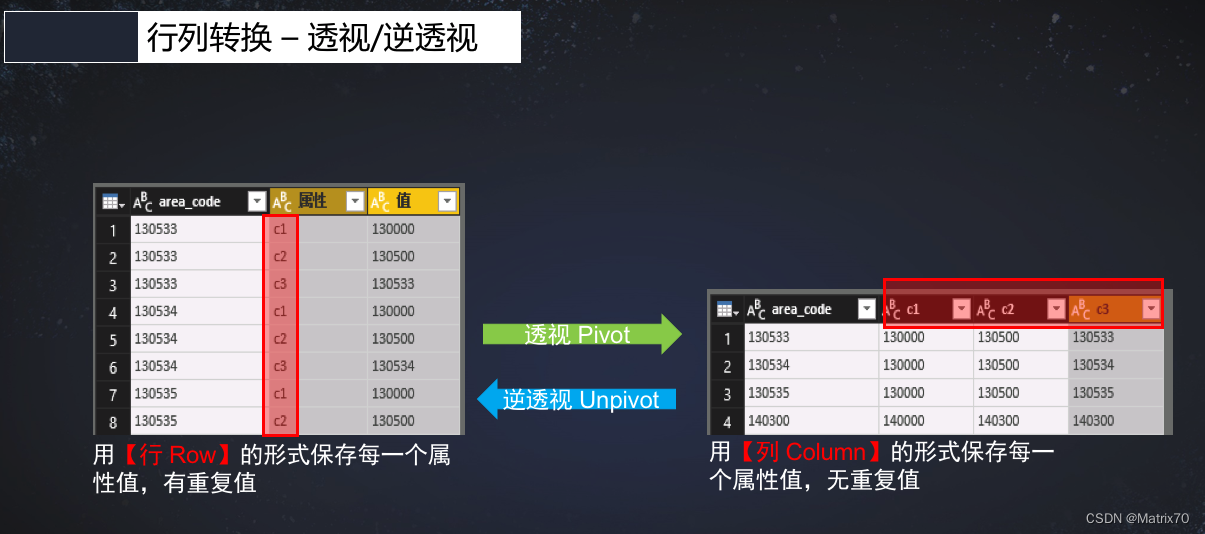
SparkOnHive_列转行、行转列生产操作(透视和逆透视)
前言 行专列,列转行是数开不可避免的一步,尤其是在最初接触Hive的时候,看到什么炸裂函数,各种udf,有点发憷,无从下手,时常产生这t怎么搞,我不会啊? 好吧ÿ…...

【人机交互 复习】第2章 Hadoop
一、概念 1.Hadoop 是一个能够对大量数据进行分布式处理的软件框架,并 且是以一种可靠、高效、可伸缩的方式进行处理的, 2.特点: 高可靠性,高效性,高可扩展性,高容错性 运行在Linux平台上,支持…...

国产自研编程语言“仓颉”来了!
在 6.21 召开的华为开发者大会(HDC2024)上,华为自研的国产编程语言“仓颉”终于对外正式发布了! 随着万物互联以及智能时代的到来,软件的形态将发生巨大的变化。一方面,移动应用和移动互联网领域仍然强力驱动人机交互…...

Swarm 集群管理
Swarm 集群管理 简介 Docker Swarm 是 Docker 的集群管理工具。它将 Docker 主机池转变为单个虚拟 Docker 主机。 Docker Swarm 提供了标准的 Docker API,所有任何已经与 Docker 守护程序通信的工具都可以使用 Swarm 轻松地扩展到多个主机。 支持的工具包括但不限…...

从社交网络到元宇宙:Facebook的战略转型
随着科技的迅猛发展和数字化时代的深入,社交网络已不再局限于简单的信息交流和社交互动,而是逐步向更广阔、更深远的虚拟现实空间——元宇宙(Metaverse)转变。作为全球最大的社交网络平台之一,Facebook正在积极推动这一…...
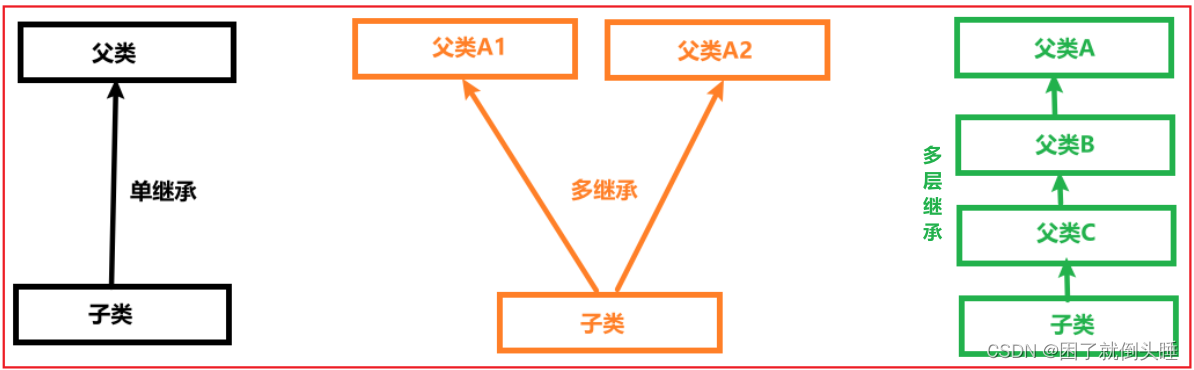
程序猿大战Python——面向对象——继承进阶
方法重写 目标:掌握方法的重写。 当父类的同名方法达不到子类的要求,则可以在子类中对方法进行重写。语法: class 父类名(object):def 方法A(self):代码... class 子类名(父类名):def 方法A(self):代码... 例如,一起来完成&…...
【Linux基础】SSH登录
SSH简介 安全外壳协议(Secure Shell Protocol,简称SSH)是一种加密的网络传输协议,可在不安全的网络中为网络服务提供安全的传输环境。 SSH通过在网络中建立安全隧道来实现SSH客户端与服务器之间的连接。 SSH最常见的用途是远程登…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
