重温线性代数
前言
对于普通的数学工作者而言,掌握矩阵、线性空间的基本性质和用法比领会抽象的概念更实用。数学专业的同学需要全面深入学习近世代数的理论和演绎法则,例如模的概念和运算。
总之,我个人认为,不论是微积分、还是线性代数,或者是统计学,多从有形的例子着手,学习最核心最实用的部分,辅以一定数量的习题练习,是一种有效的学习方法。
向量空间->线性变换->线性变换的表示:矩阵
线性代数的核心思想
任何一个n维空间中的元素,都可以通过一个向量(x1,x2,...,xn)(x_1, x_2, ...,x_n)(x1,x2,...,xn)来定位,或者说n维空间中每个点,都有一个坐标。有的书上也把这种n维空间叫向量空间。
矩阵是什么?以下几种理解都是正确的:
- 一个矩阵可以表示从n维空间到m维空间的线性变换,或者叫映射
- 一个矩阵对应了一个运动
- 一个矩阵对应了一个坐标系。因为运动既可以看成是点的运动,也可以看成是坐标系的运动。如果选取了某个坐标系作为标准坐标系(或者叫参照坐标系),那其它坐标系的基就可以表示成这个参照系的线性组合,也就是每个基对应一个向量,那所有基的坐标就构成了一个矩阵。
所以,一个矩阵乘以一个向量: A∗xA*xA∗x 就是把一个向量映射到一个新的向量。这个矩阵的每一行对应的是新的坐标系的基的坐标。为什么矩阵乘法定义为向量内积的方式?因为内积代表着新的向量在旧的向量上的投影。
这里需要举个例子才能说得更明白。
基本概念
特征值,特征向量,行列式,trace。
矩阵的乘法
基本性质
- 行列式为0 = 不满秩 = 不可逆
- 行列式等于特征值的乘积
- 二维矩阵的行列式等于平行四边形的面积,三维矩阵的行列式对应的是平行六面体的体积…更高维度上也可以延伸出同样的类似于“体积”的定义。
- 对称矩阵的特征向量相互之间正交
- 矩阵的迹(trace)等于特征值之和
矩阵的相似
TODO
矩阵的分解和分块计算
A 有n 个相异的特征值, 则A 可对角化
书籍推荐
- 线性代数方法导引-屠伯埙
- 高等代数-屠伯埙: 我本科时的线性代数教材,屠伯埙亲自指导上课。
相关文章:

重温线性代数
前言 对于普通的数学工作者而言,掌握矩阵、线性空间的基本性质和用法比领会抽象的概念更实用。数学专业的同学需要全面深入学习近世代数的理论和演绎法则,例如模的概念和运算。 总之,我个人认为,不论是微积分、还是线性代数&…...

2023河北沃克HEGERLS甘肃金昌重型仓储项目案例|托盘式四向穿梭车智能密集存储系统在工业行业的创新应用
项目名称:自动化仓储托盘式四向穿梭车智能密集立体库项目 项目合作客户:甘肃省金昌市某集团企业 项目施工地域:甘肃省金昌市 设计与承建单位:河北沃克金属制品有限公司(自主品牌:海格里斯HEGERLS&#x…...

软件测试的案例分析 - 闰年5
文章目的 显示不同的博客能获得多少博客质量分 (这是关于博客质量分的测试 https://www.csdn.net/qc) 这个博客得了 83 分。怎么才能得到更多分数? 正文 我们谈了不少测试的名词, 软件是人写的, 测试计划和测试用例也是人写的, 人总会犯错误。错误发生…...

Linux文件基础I/O
文件IO文件的常识基础IO为什么要学习操作系统的文件操作C语言对于函数接口的使用接口函数介绍如何理解文件文件描述符重定向更新给模拟实现的shell增加重定向功能为什么linux下一切皆文件?文件的常识 1.空文件也要在磁盘占据空间 2.文件 内容 属性 3.文件操作 对…...
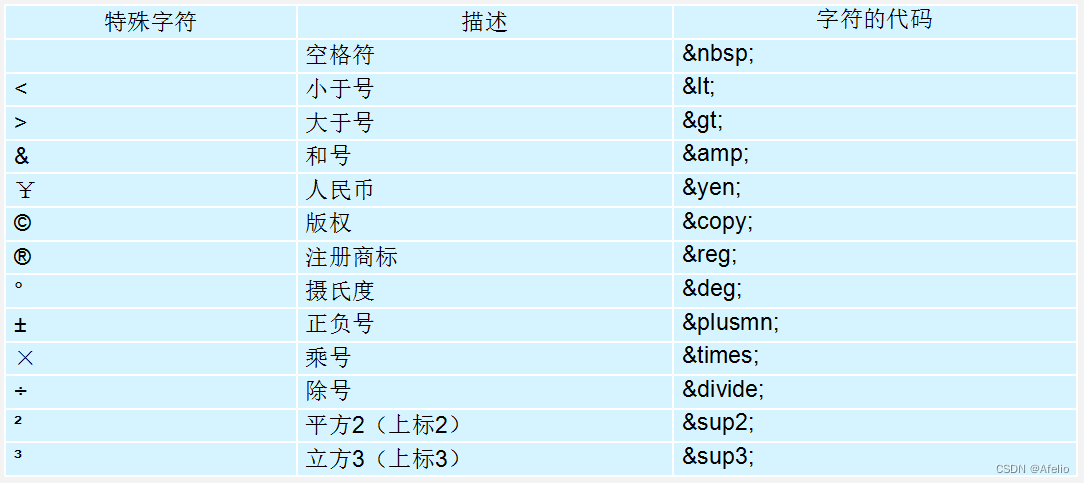
HTML看这一篇就够啦,HTML基础大全,可用于快速回顾知识,面试首选
HTML 1 基础 1.1 DOCTYPE <!DOCTYPE> 文档类型声明,作用就是告诉浏览器使用哪种HTML版本来显示网页。 <!DOCTYPE html> 这句代码的意思是: 当前页面采取的是 HTML5 版本来显示网页. 注意: 声明位于文档中的最前面的位置,处于 标签之前。 …...
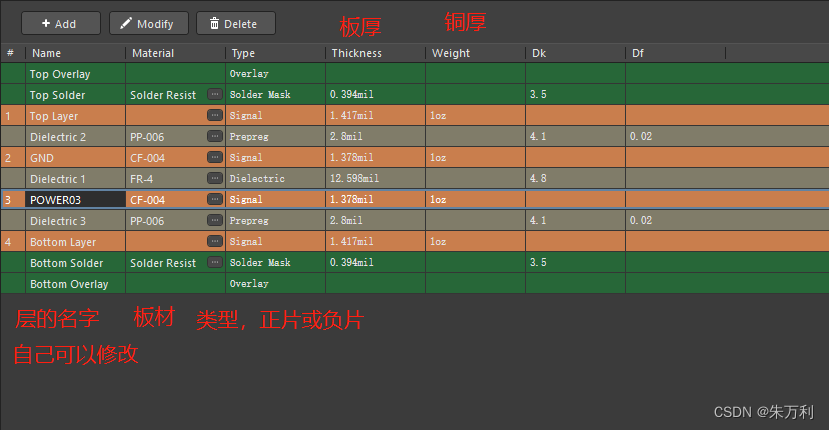
Altium Designer(AD)软件使用记录05-PCB叠层设计
目录Altium Designer(AD)软件使用记录05-PCB叠层设计一、正片层和负片层的介绍1、正片层(Signal)2、负片层(Plane)3、内电层的分割实现二、正片层和负片层的内缩设计1、负片设置内缩20H原则2、正片铺铜设置内缩1、设置规则2、重新铺铜三、AD的层叠设计四、叠层设计需要注意的问…...
ArcGIS动态表格批量出图
一.产品介绍:ArcGIS动态表格扩展模块Mapping and Charting Solutions,可用于插入动态表格,与数据驱动结合,出图效率无敌。注:优先选择arcgis10.2.2。 二、下载连接: https://www.xsoftnet.com/share/a001CX…...

ChatGPT真神奇,但是也真焦虑
ChatGPT火爆ChatGPT的火爆程度不用说也知道。就目前来说,已经开始冲击各行业了,比如客服、智能助手、语言学习、自然语言处理等等等。。ChatGPT冲击冲击最高的可能就是中间这个段位的了。高段位无法取代,但是低段位,通过使用ChatG…...
mos管驱动与米勒平台介绍、消除
mos驱动设计 1.选择适当的驱动芯片 为了控制MOSFET,需要使用专门的驱动芯片。选择合适的芯片需要考虑MOSFET的电压和电流需求。常见的驱动芯片包括IR2110、IR2184、MIC4424等。 2.设计电路 在驱动电路中,需要加入一些电路元件来保证MOSFET的顺畅工作…...

20230311英语学习
Philosophy of Food: Guidelines for an Authentic Approach to Eating 饮食哲学:值得思考的问题 Whats Philosophical About Food? Philosophy of food finds its basis on the idea that food is a mirror.Eating mirrors the making of a self, that is, the …...
)
【面试题】Nginx面试题汇总(无解答)
什么是Nginx?谈谈个人都理解,项目中是否用到,为什么要用,有什么优点?为什么要用Nginx?为什么Nginx性能这么高?Nginx怎么处理请求的?什么是正向代理和反向代理?使用“反向…...
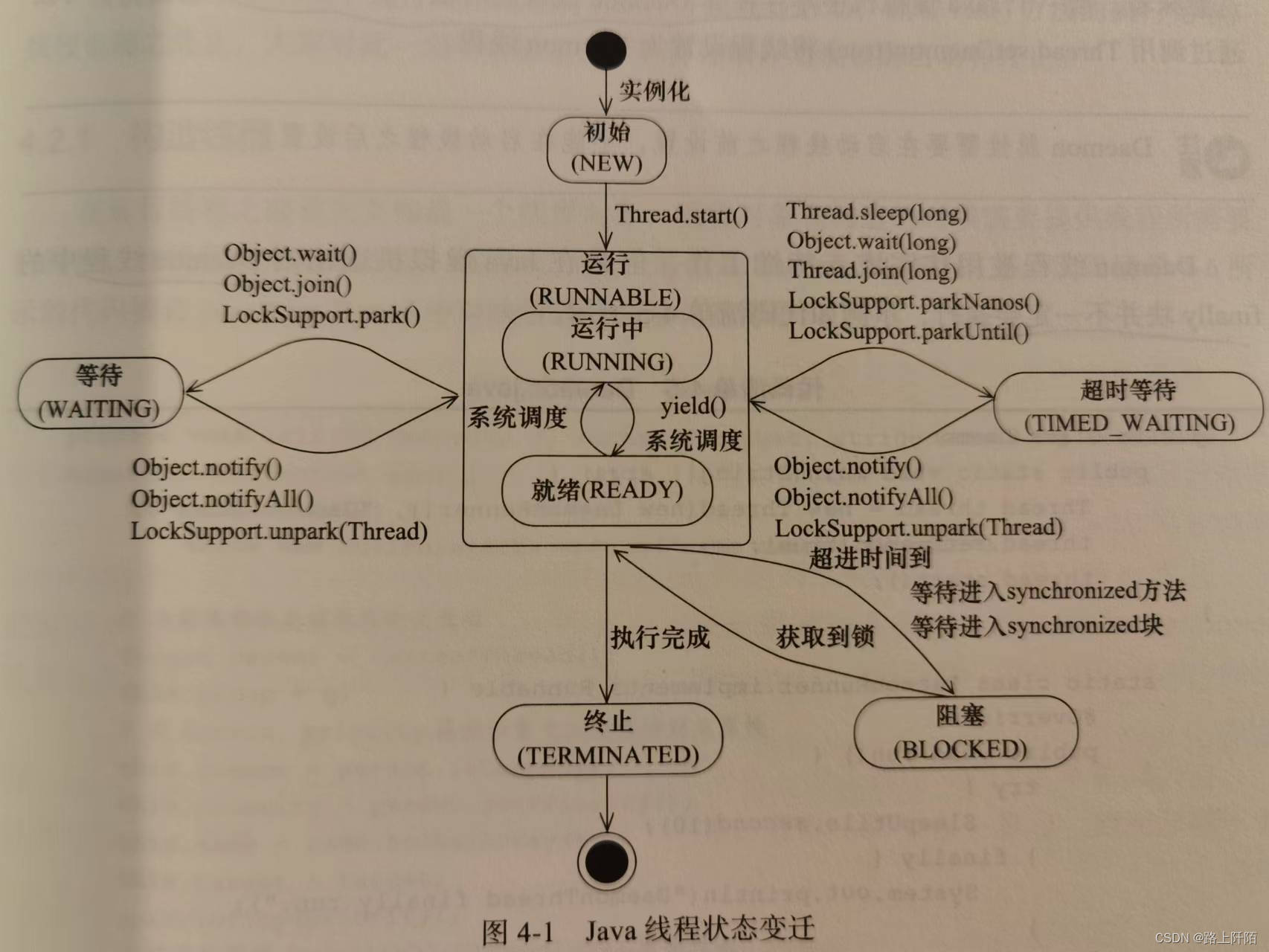
Java面试总结(六)
进程和线程的区别 根本区别: 进程时操作系统资源分配的基本单位,而线程是处理器任务调度和执行的基本单位。 资源开销: 每个进程都有自己独立的代码和数据空间(程序上下文),进程之间的切换开销比较大&…...
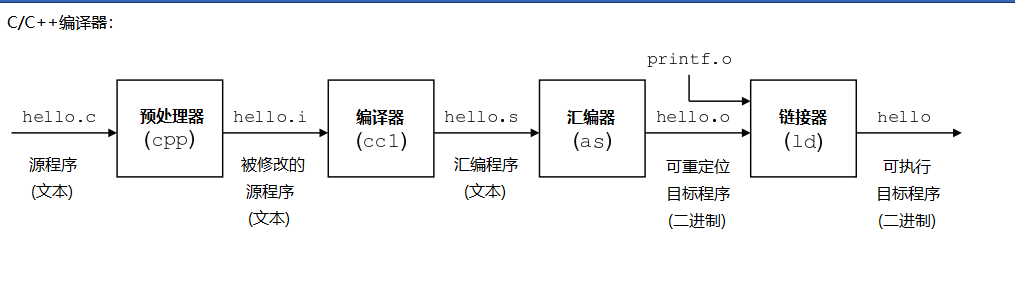
Windows逆向安全(一)C与汇编的关系
前言 逆向是一种新型的思维模式也是软件开发领域中极为重要的技术,涵盖各种维度去深挖软件架构的本质和操作系统原理,学习逆向后可以在各领域中发挥至关重要的作用,其中包括黑灰色,安全开发,客户端安全,物…...

Lazada、Allegro、速卖通测评自养号技术(方法解析)
无论是亚马逊、拼多多Temu、shopee、Lazada、wish、速卖通、煤炉、敦煌、雅虎、eBay、TikTok、Newegg、乐天、美客多、阿里国际、沃尔玛、OZON、Joom、Facebook、Coupang、独立站、Cdiscount、Kaufland、DARTY、Allegro、MANO等平台测评自养号对于卖家来说算是一种低成本、高回…...

Vue3的composition API—setup函数, ref函数,reactive函数
1、Setup 函数 1.setup 是vue3中的一个配置项 2、setup是所有组件所需要的数据和方法都需要配置到setup中的 3、setup两种返回值: 若返回一个对象 若返回一个渲染函数 mian.js文件 注意:尽量不与Vue2混用 setup中无法访问vue2中的配置 不能是async函数…...

国外seo比较好的优化方法有哪些?
随着互联网的不断发展,SEO(搜索引擎优化)变得越来越重要。 对于国外市场,Google搜索引擎是最为重要的搜索引擎之一, 因此在优化国外网站时,需要将Google SEO优化作为首要任务。 关键词研究和优化 在进行…...

【JavaEE进阶】——第一节.Maven国内源配置
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 操作步骤 1.打开项目配置界面(当前项目配置) 2.检查并配置国内源 3.再次打开项目配置界面(新项目配置) 4…...

dockerFile编写
dockerFile编写 语法参数 # DockerFile常用指令 USER # 指定运行的用户,一般不用配置 FROM # 拉取基础镜像,一切从这里开始构建 ARG # 构建参数,只能在dockerFile中使用, # eg: JAR_FILEtarget/springboot-mongo-0.0.1-SNAPSHOT.jar MAI…...
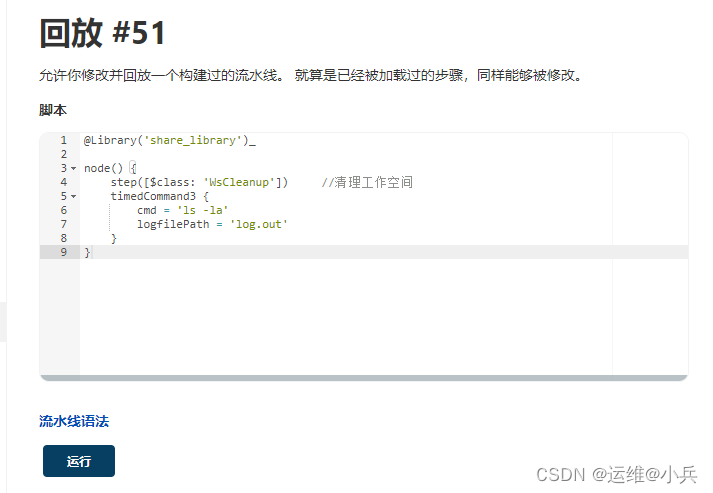
jenkins扩展你的流水线
文章目录一、概述二、可信库和不可信库可信库不可信库三、内部库与外部库内部库SSH访问HTTP 访问外部库配置一个外部库四、在流水线脚本中使用库从源码版本控制中自动下载库加载库到脚本中Library 注解库步骤库指令五、Jenkins 项目中的库范围六、共享库代码的结构src示例一&am…...

Golang模糊测试入门
本教程介绍了 Go 中模糊测试的基础知识。通过模糊测试,随机数据会针对您的测试运行,以试图找到漏洞或导致崩溃的输入。可以通过模糊测试发现的一些漏洞示例包括 SQL 注入、缓冲区溢出、拒绝服务和跨站点脚本攻击。 在本教程中,您将为一个简单的函数编写模糊测试,运行 go 命…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
