线性代数|机器学习-P15矩阵A的低秩变换下的逆矩阵
文章目录
- 1. 单位矩阵的秩1变换
- 1.1 功能说明
- 1.2 证明
- 2. 单位矩阵 I n I_n In的秩k变换
- 3. 一般矩阵A的秩k变换
- 4. 公式用途
- 4.1 求解方程
- 4.2 卡曼滤波
1. 单位矩阵的秩1变换
1.1 功能说明
假设我们有一个单位矩阵I,列向量u,v那么当我们对单位向量I减去秩为1的矩阵后,其逆等于多少?
M = I − u v T , M − 1 = I + u v T 1 − v T u \begin{equation} M=I-uv^T,M^{-1}=I+\frac{uv^T}{1-v^Tu} \end{equation} M=I−uvT,M−1=I+1−vTuuvT
- 我们发现,对于单位矩阵进行秩为1的扰动 u v T uv^T uvT,其逆也是进行秩为1的扰动 u v T 1 − v T u \frac{uv^T}{1-v^Tu} 1−vTuuvT,这个公式的好处在于,当我们知道对I的秩为1的扰动,就能通过公式直接知道其逆的扰动,真神奇!
1.2 证明
M = I − u v T ⇒ M − 1 = I + u v T 1 − v T u \begin{equation} M=I-uv^T\Rightarrow M^{-1}=I+\frac{uv^T}{1-v^Tu}\end{equation} M=I−uvT⇒M−1=I+1−vTuuvT
- 定义矩阵E表示如下:
E = [ I u v T 1 ] , D e t [ E ] = 1 − v T u (3) E=\begin{bmatrix}I&&u\\\\v^T&&1\end{bmatrix},Det[E]=1-v^Tu\tag{3} E= IvTu1 ,Det[E]=1−vTu(3)
我们想求 E − 1 E^{-1} E−1,可以通过增广矩阵,进行行变换得到, - 第一种方法是:将第一行乘以 v T v^T vT后加到第二行中.
[ I 0 − v T 1 ] E = [ I u 0 D ] (4) \begin{bmatrix}I&&0\\\\-v^T&&1\end{bmatrix}E=\begin{bmatrix}I&&u\\\\0&&D\end{bmatrix}\tag{4} I−vT01 E= I0uD (4)
E − 1 = [ I u 0 D ] − 1 [ I 0 − v T 1 ] = [ I + u D − 1 v T − u D − 1 − D − 1 v T D − 1 ] (5) E^{-1}=\begin{bmatrix}I&&u\\\\0&&D\end{bmatrix}^{-1}\begin{bmatrix}I&&0\\\\-v^T&&1\end{bmatrix}=\begin{bmatrix}I+uD^{-1}v^T&&-uD^{-1}\\\\-D^{-1}v^T&&D^{-1}\end{bmatrix}\tag{5} E−1= I0uD −1 I−vT01 = I+uD−1vT−D−1vT−uD−1D−1 (5) - 第二种方法是:将第二行乘以 u u u后加到第一行中.
[ I − u 0 1 ] E = [ I − u v T 0 v T 1 ] (6) \begin{bmatrix}I&&-u\\\\0&&1\end{bmatrix}E=\begin{bmatrix}I-uv^T&&0\\\\v^T&&1\end{bmatrix}\tag{6} I0−u1 E= I−uvTvT01 (6)
E − 1 = [ I − u v T 0 v T 1 ] − 1 [ I − u 0 1 ] = [ M − 1 − M − 1 u − v T M − 1 1 + v T M − 1 u ] (7) E^{-1}=\begin{bmatrix}I-uv^T&&0\\\\v^T&&1\end{bmatrix}^{-1}\begin{bmatrix}I&&-u\\\\0&&1\end{bmatrix}=\begin{bmatrix}M^{-1}&&-M^{-1}u\\\\-v^TM^{-1}&&1+v^TM^{-1}u\end{bmatrix}\tag{7} E−1= I−uvTvT01 −1 I0−u1 = M−1−vTM−1−M−1u1+vTM−1u (7) - 由公式4,6 可得,两个 E − 1 E^{-1} E−1相等, M = I − u v T M=I-uv^T M=I−uvT
[ I + u D − 1 v T − u D − 1 − D − 1 v T D − 1 ] = [ M − 1 − M − 1 u − v T M − 1 1 + v T M − 1 u ] (8) \begin{bmatrix}I+uD^{-1}v^T&&-uD^{-1}\\\\-D^{-1}v^T&&D^{-1}\end{bmatrix}=\begin{bmatrix}M^{-1}&&-M^{-1}u\\\\-v^TM^{-1}&&1+v^TM^{-1}u\end{bmatrix}\tag{8} I+uD−1vT−D−1vT−uD−1D−1 = M−1−vTM−1−M−1u1+vTM−1u (8) - 由第一个行,第一列可得如下
M − 1 = I + u D − 1 v T = I + u v T 1 − v T u (9) M^{-1}=I+uD^{-1}v^T=I+\frac{uv^T}{1-v^Tu}\tag{9} M−1=I+uD−1vT=I+1−vTuuvT(9) - 结论:
M = I − u v T ⇒ M − 1 = I + u v T 1 − v T u (10) M=I-uv^T\Rightarrow M^{-1}=I+\frac{uv^T}{1-v^Tu}\tag{10} M=I−uvT⇒M−1=I+1−vTuuvT(10)
2. 单位矩阵 I n I_n In的秩k变换
- 定义 M 表示如下:
M = I − U V T → M − 1 = I n + U ( I k − V T U ) − 1 V T \begin{equation} M=I-UV^T\rightarrow M^{-1}=I_n+U(I_k-V^TU)^{-1}V^T \end{equation} M=I−UVT→M−1=In+U(Ik−VTU)−1VT - 同理构造矩阵E
E = [ I n U V T I k ] , d e t ( E ) = d e t ( I n − U V T ) \begin{equation} E=\begin{bmatrix}I_n&U\\\\V^T&I_k\end{bmatrix},det(E)=det(I_n-UV^T) \end{equation} E= InVTUIk ,det(E)=det(In−UVT)
3. 一般矩阵A的秩k变换
Sherman-Morrison-Woodbury formula- 定义 M 表示如下:
M = A − U V T \begin{equation} M=A-UV^T \end{equation} M=A−UVT
- M − 1 = A − 1 + A − 1 U ( I − V T A − 1 U ) − 1 V T A − 1 \begin{equation} M^{-1}=A^{-1}+A^{-1}U(I-V^TA^{-1}U)^{-1}V^TA^{-1} \end{equation} M−1=A−1+A−1U(I−VTA−1U)−1VTA−1 - 同理构造矩阵E
E = [ A U V T I ] , d e t ( E ) = d e t ( A − U V T ) \begin{equation} E=\begin{bmatrix}A&U\\\\V^T&I\end{bmatrix},det(E)=det(A-UV^T) \end{equation} E= AVTUI ,det(E)=det(A−UVT)
4. 公式用途
4.1 求解方程
( I k − U V T ) x = b → x = [ I n + U ( I k − V T U ) − 1 V T ] b \begin{equation} (I_k-UV^T)x=b\rightarrow x=[I_n+U(I_k-V^TU)^{-1}V^T] b \end{equation} (Ik−UVT)x=b→x=[In+U(Ik−VTU)−1VT]b
4.2 卡曼滤波
当我们有一个已知的方程解 A x = b Ax=b Ax=b,最小二乘的结果如下:
A T A x ^ = A T b \begin{equation} A^TA\hat{x}=A^Tb \end{equation} ATAx^=ATb
- 突然我们需要新增一行数据 v T v^T vT,那么矩阵变成如下:
[ A T v ] [ A v T ] x ^ = [ A T v ] [ b b m + 1 ] \begin{equation} \begin{bmatrix}A^T&v\end{bmatrix} \begin{bmatrix}A\\\\v^T\end{bmatrix}\hat{x}=\begin{bmatrix}A^T&v\end{bmatrix} \begin{bmatrix}b\\\\b_{m+1}\end{bmatrix} \end{equation} [ATv] AvT x^=[ATv] bbm+1 - 整理可得如下:
[ A T A + v v T ] x ^ = A T b + v b m + 1 \begin{equation} [A^TA+vv^T]\hat{x}=A^Tb+vb_{m+1} \end{equation} [ATA+vvT]x^=ATb+vbm+1 - 我们发现原来的矩阵为 A T A A^TA ATA,后来加了一个秩1的矩阵 v v T vv^T vvT,那么在假设原来 A T A A^TA ATA可逆的情况下,可以直接通过公式求得:
M = A T A − v v T \begin{equation} M=A^TA-vv^T \end{equation} M=ATA−vvT
M − 1 = ( A T A ) − 1 + ( A T A ) − 1 v ( I + v T ( A T A ) − 1 v ) − 1 v T ( A T A ) − 1 \begin{equation} M^{-1}=(A^TA)^{-1}+(A^TA)^{-1}v(I+v^T(A^TA)^{-1}v)^{-1}v^T(A^TA)^{-1} \end{equation} M−1=(ATA)−1+(ATA)−1v(I+vT(ATA)−1v)−1vT(ATA)−1
这样就可以在原来的结果基础上直接得到新解。
相关文章:

线性代数|机器学习-P15矩阵A的低秩变换下的逆矩阵
文章目录 1. 单位矩阵的秩1变换1.1 功能说明1.2 证明 2. 单位矩阵 I n I_n In的秩k变换3. 一般矩阵A的秩k变换4. 公式用途4.1 求解方程4.2 卡曼滤波 1. 单位矩阵的秩1变换 1.1 功能说明 假设我们有一个单位矩阵I,列向量u,v那么当我们对单位向量I减去秩为1的矩阵…...

强强联合 极光推送(JPush)成为华为生态市场首家推送类SDK服务商
近日,中国领先的客户互动和营销科技服务商,极光(Aurora Mobile,纳斯达克股票代码:JG)的核心产品极光推送(JPush)顺利通过华为开发者联盟的多项测试及审核,成为首家在Harm…...

防止在 Qt 中触发信号
在 Qt 中工作时,有时我们需要暂时阻止某些信号的触发。以下是一个经典场景:我们有一个 QCheckBox 对象,当用户勾选或取消勾选时,需要调用一个函数,因此我们将这个函数连接到 stateChanged(int state) 信号。然而&#…...
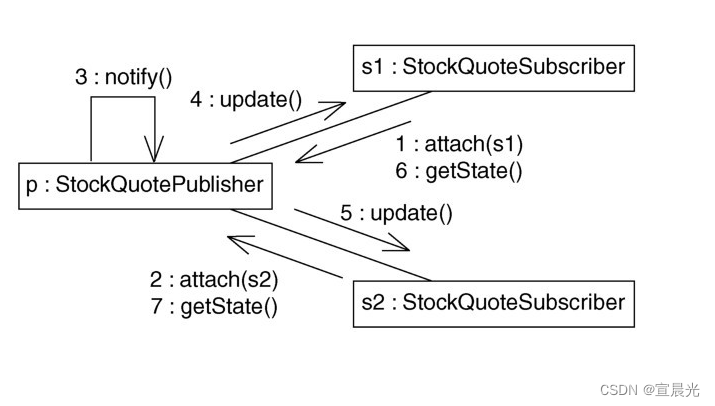
【UML用户指南】-17-对基本行为建模-交互
目录 1、消息的可视化表示 2、对象与角色 3、链和连接件 4、消息 5、序列 6、创建、修改和撤销 7、表示法 8、常用建模技术 8.1、对控制流建模 8.1.1、基于时间的控制流 8.1.2、基于结构的控制流 在任何有意义的系统中,对象都不是孤立存在的,…...

Java中的类加载器与热部署技术详解
Java中的类加载器与热部署技术详解 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在软件开发中,特别是在大型应用和服务的开发过程中,类…...
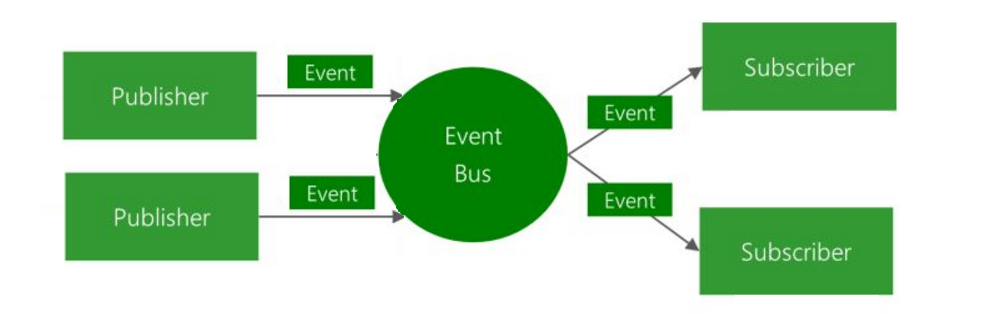
【事件总线】EventBus
文章目录 概述如何使用如何发布消息如何进行消息监听 来源 概述 事件总线是对发布-订阅模式(观察者)的一种实现,是一种集中式事件处理机制,允许不同的组件之间进行彼此通信而又不需要相互依赖,达到一种解耦的目的。 …...
LeetCode 热题100 --双指针
双指针 b站UP主蜜糖:由于数据特征的有序性(大小或者正负),所以可以证明当前节点一定是优于过往节点,从而可以通过数据的维度数量的指针,逐步的迭代收敛最终找到最优解。 283.移动零 相关标签 :…...

从《深入设计模式》一书中学到的编程智慧
软件设计原则 优秀设计的特征 在开始学习实际的模式前,让我们来看看软件架构的设计过程,了解一下需要达成目标与需要尽量避免的陷阱。 代码复用 无论是开发何种软件产品,成本和时间都最重要的两个维度。较短的开发时间意味着可比竞争对…...

Redis 基本配置
Redis的配置文件通常位于 /etc/redis/redis.conf。以下是一些常见的Redis配置选项和它们的说明: 基本配置 1. 绑定地址 bind 127.0.0.1默认情况下,Redis只监听本地接口。如果需要远程访问,可以修改成bind 0.0.0.0,不过这会带来…...
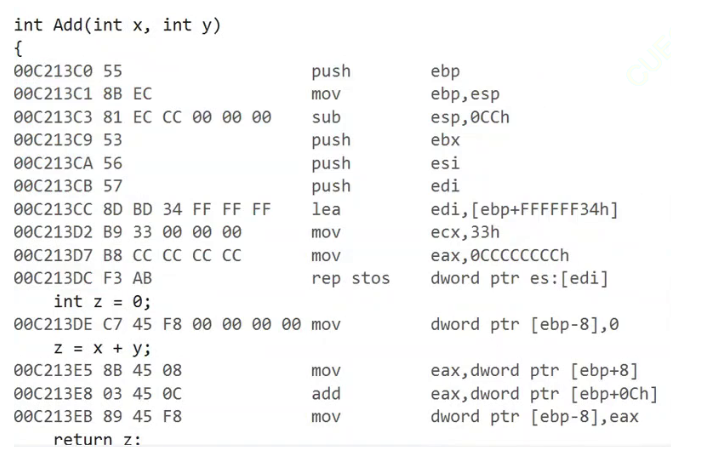
【C++庖丁解牛】函数栈帧的创建与销毁
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 1. 寄存器2. ebp和esp是如…...
Java基础16(集合框架 List ArrayList容器类 ArrayList底层源码解析及扩容机制)
目录 一、什么是集合? 二、集合接口 三、List集合 四、ArrayList容器类 1. 常用方法 1.1 增加 1.2 查找 int size() E get(int index) int indexOf(Object c) boolean contains(Object c) boolean isEmpty() List SubList(int fromindex,int …...

数组:移除元素
参考资料:代码随想录 本题思路:通过快慢指针将两次循环减少到一次 class Solution {public int removeElement(int[] nums, int val) {//0 1 2 2 2 2 3int fast 0;int slow 0;while(fast < nums.length){if(nums[fast] ! val){nums[slow] nums[f…...
——通信杂谈(完结))
胡说八道(24.6.22)——通信杂谈(完结)
上回书说到雷达和香农的信息论,今天来进行完结。 数字幅值调制或幅值键控(ASK)调制方式是指载波信号的幅值随数字基带信号而变化,因此可以实现将基带信号搬移到载波频段。2ASK是利用代表数字信息0或1的基带矩形脉冲去键控一个连续…...
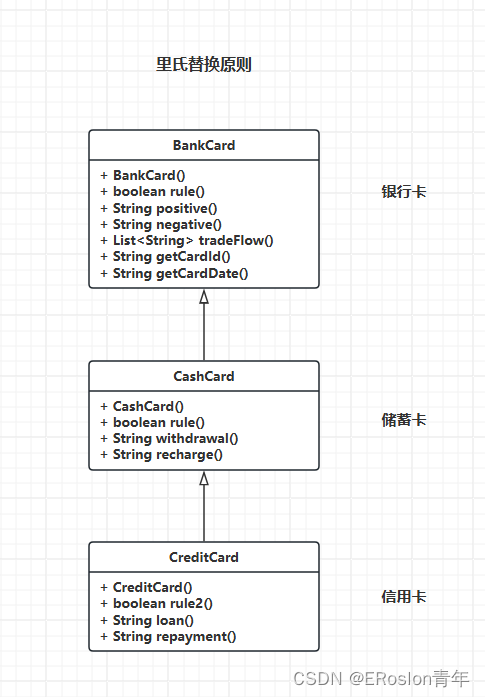
设计模式原则——里氏替换原则
设计模式原则 设计模式示例代码库地址: https://gitee.com/Jasonpupil/designPatterns 里氏替换原则 继承必须确保父类所拥有的性质在子类中依然成立 与开闭原则不同的是开闭原则可以改变父类原有的功能,里氏替换原则不能修改父类的原有的性质&#…...

详解 ClickHouse 的 SQL 操作
传统关系型数据库(以 MySQL 为例)的 SQL 语句,ClickHouse 基本都支持 一、插入 --语法: insert into table_name values(xxxxxx),(yyyyyyy),...;insert into table_name select xxxxx from table_name2 where yyyyy;二、更新和删…...

WPF与Winform,你的选择是?
概述 在桌面应用的发展历程中,Winform和WPF作为微软推出的两大框架,各自承载着不同的设计理念和技术特色。Winform以其稳定、成熟的技术基础,长期占据着企业级应用开发的重要地位。而WPF,作为后来者,以其现代化的UI设计…...

基于SpringBoot的实习管理系统设计与实现
你好呀,我是计算机学姐码农小野!如果有相关需求,可以私信联系我。 开发语言: Java 数据库: MySQL 技术: SpringBoot框架,B/S模式 工具: MyEclipse,Tomcat 系统展示 …...

编程用什么电脑不卡的:深度解析与推荐
编程用什么电脑不卡的:深度解析与推荐 在编程的世界里,一台流畅不卡的电脑无疑是每个开发者的得力助手。然而,面对市场上琳琅满目的电脑品牌和型号,如何选择一台适合编程的电脑却成为了一个令人困惑的问题。本文将从四个方面、五…...

优先级队列模拟实现
目录 1.堆的概念 2.堆性质堆中的某个元素小于或大于他的左右孩子 3.小根堆实例 4.堆创建 4.1调整思路 4.2向下调整思路 4.3代码实现(大根堆) 5.堆的删除 6.堆的插入 7.常用接口 7.1PriorityQueue和PriorityBlockingQueue 1.堆的概念 如果有一…...
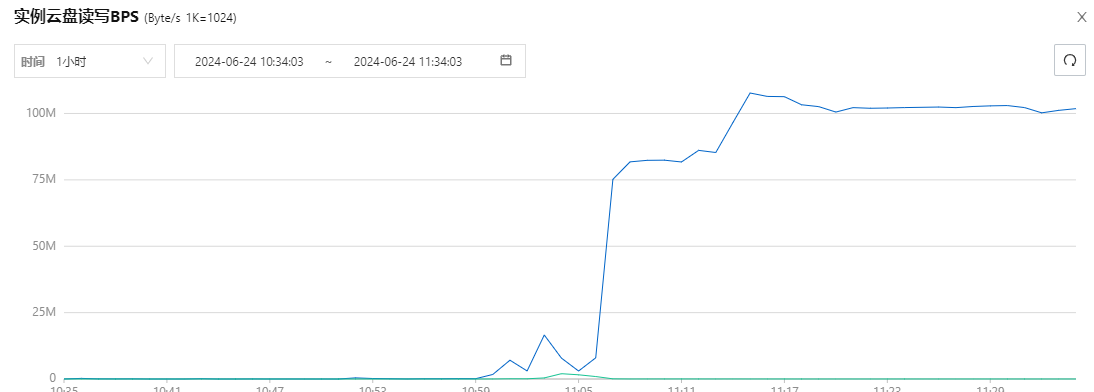
记一次服务器崩溃事件
今天在安装Jenkins的时候,进行到插件安装这一步,本来一切顺利,结果最后安装完成之后一直进不去网页,显示连接超时,网上搜索了一圈也没发现什么相似的情况,当我疑惑的时候回到Linux控制台,发现命…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

基于小程序老人监护管理系统源码数据库文档
摘 要 近年来,随着我国人口老龄化问题日益严重,独居和居住养老机构的的老年人数量越来越多。而随着老年人数量的逐步增长,随之而来的是日益突出的老年人问题,尤其是老年人的健康问题,尤其是老年人产生健康问题后&…...
