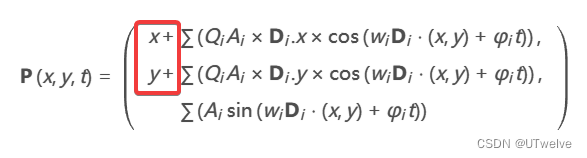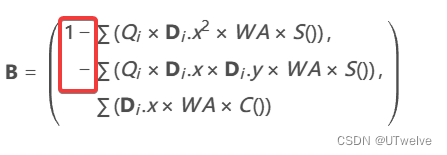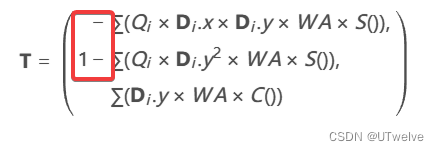虚幻引擎 Gerstner Waves -GPU Gems 从物理模型中实现有效的水体模拟
这篇文章重点在于结合GPU Gems一书中有关Gerstner Waves 的数学公式,在虚幻引擎中复现正确的Gerstner Waves和正确的法线
文中内容整理自书中,并附带我的理解,与在虚幻引擎中的实现,可以参考原文看这篇文章,原文网上很多,我这里就不转载了
内容看上去有些乱?
与虚幻无关的内容,以普通文本的形式体现,需要强调的、与虚幻有关的,我将紧挨着内容以引用块的形式附上(就像这段话)
这是因为我希望读者能随着我一起看看这本书,书讲到哪,咱们做到哪
书中还介绍了几种波,我假设你们做了课前预习,本文直接开始G波
1.2.1选择波形
我们需要一组参数来定义每个波形。这些参数包括:
- Wavelength 波长( L L L )
- 世界空间中波峰到波峰之间的距离。
- 波长 L L L 与角频率 w w w 之间的关系为 w = 2 π L w = \frac{2\pi}{L} w=L2π。
这里将会出现第一个坑,如果你看的是英伟达的来源,他们在公式中弄丢了这个π,这篇文章中的公式将使用原书公式
-
Amplitude 振幅( A A A )
- 从水平面到波峰的高度。
-
Speed 速度( S S S )
- 波峰每秒前进的距离。 将速度表示为相位常数 φ \varphi φ 更为方便。
- φ = S × 2 π L \varphi = S \times\frac{2\pi}{L} φ=S×L2π
-
Direction 方向( D D D )
- 垂直于波阵面的水平向量,波峰沿着波阵面运动。
为了在场景的动态中提供变化,我们将在一定的约束条件下随机生成这些波浪参数。随着时间的推移,我们将持续地将一个波浪渐隐,然后再以一组不同的参数将其渐显。
事实证明,这些参数是相互依赖的。必须仔细的为每个波浪生成一整套参数,这些参数需要以一种令人信服的方式组合在一起。
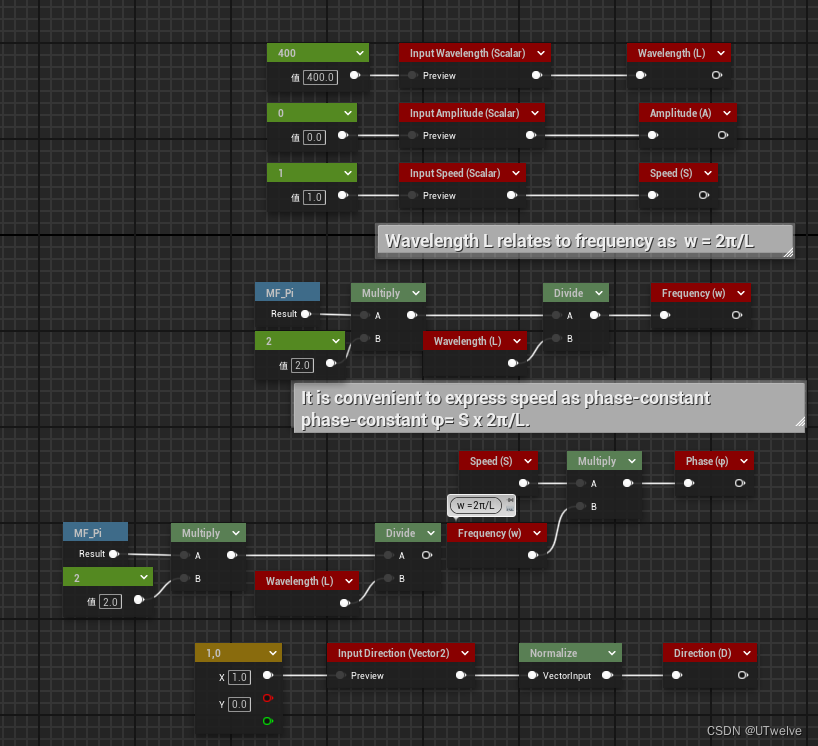
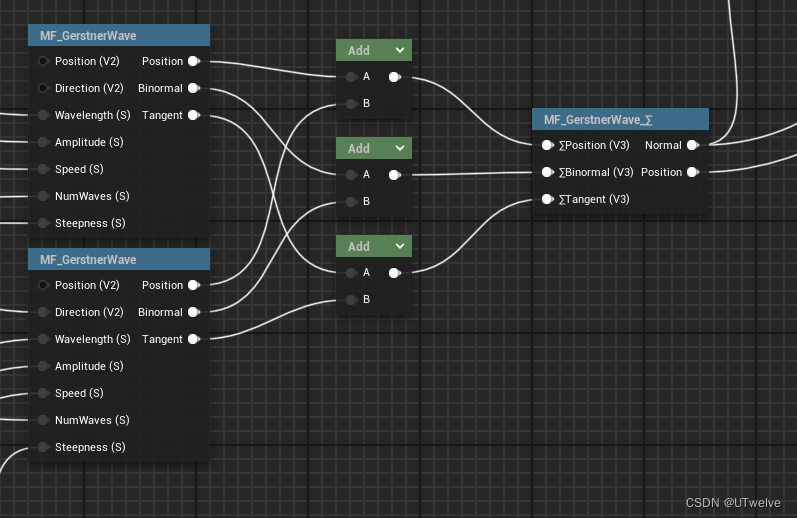
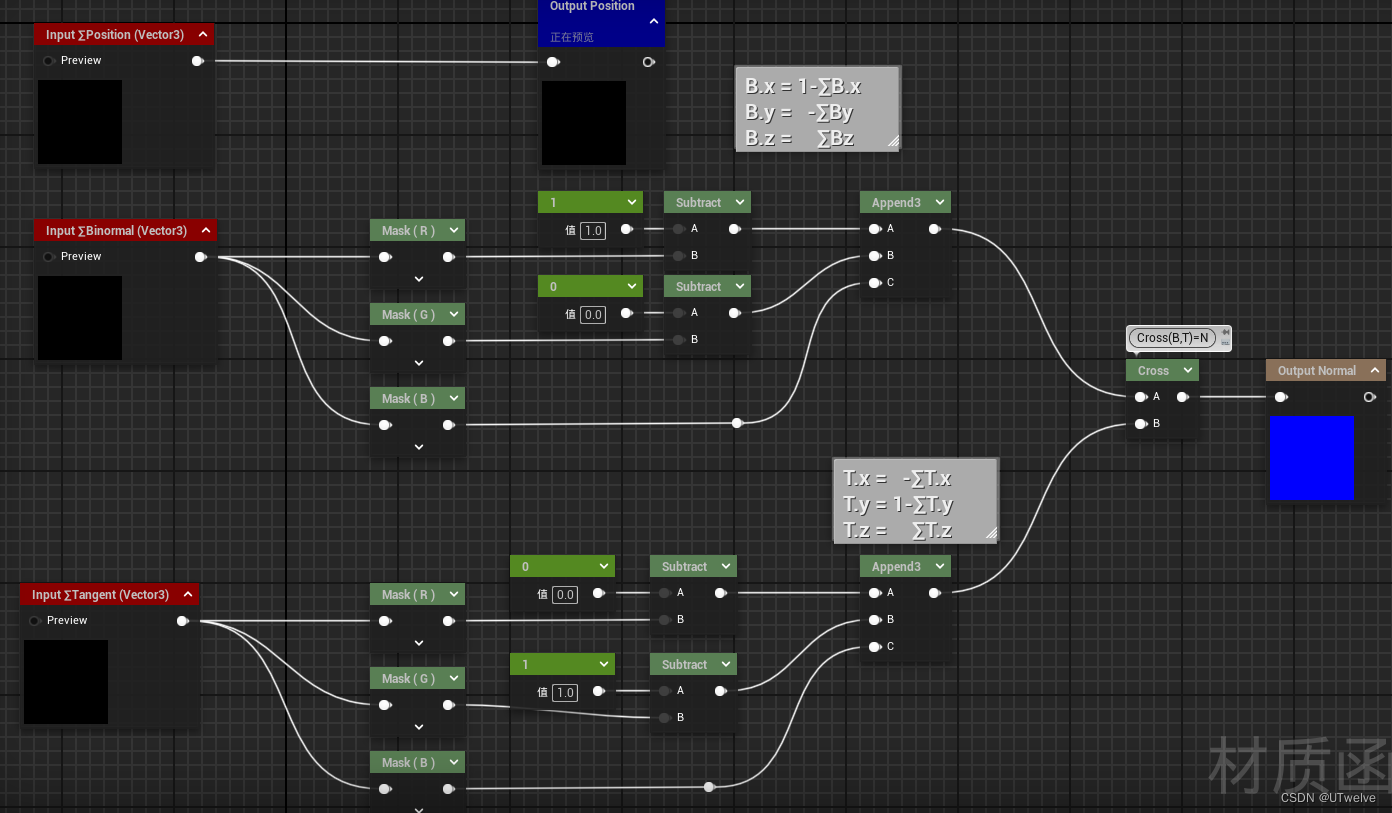
新建一个GerstnerWaves函数,我们先把上方出现的变量在input预留:
以防有疑问,最后一个Node是“重路由” ,它是用来避免蓝图变意大利面的东西,无功能上的意义
1.2.2 法线和切线
因为表面是显式函数,所以我们可以直接计算任何点的表面方向,而不需要依赖有限差分技术。
副法线向量 B B B 和切线向量 T T T 是分别 x x x 和 y y y 方向的偏导数。对于2D水平面中的任何点 ( x x x , y y y ),表面上的三维位置 P P P 是:
Equation 6a 公式6a
N ( x , y ) = B ( x , y ) × T ( x , y ) \mathbf{N}(x,y)=\mathbf{B}(x,y)\times\mathbf{T}(x,y) N(x,y)=B(x,y)×T(x,y)
这个公式体现N与B、T的关系。但我们先跳过这个,最后再来处理法线,这将规避经典的法线混合问题
格斯特纳波GerstnerWaves
为了有效的模拟,我们需要控制波浪的陡峭程度。如前所述,正弦波呈现出圆润的外观——这可能正是我们想要的平静、田园诗般的池塘效果。但对于粗犷的海面,我们需要形成更尖锐的波峰和更宽阔的波谷。我们可以使用公式8a和8b来实现所需的形状,但我们选择了相关的格斯特纳波。
GerstnerWaves早在有计算机图形学之前就被开发出来,用于在物理基础上模拟海水。因此GerstnerWaves提供了一些表面的微妙运动,这些变化不明显但是非常可信。(详细描述参见Tessendorf 2001)。
我们选择GerstnerWaves,因为它们有一个常被忽视的特性:将,这正是我们希望顶点集中的地方,如图1-5所示。

这是GerstnerWaves函数:
Equation 9 公式9
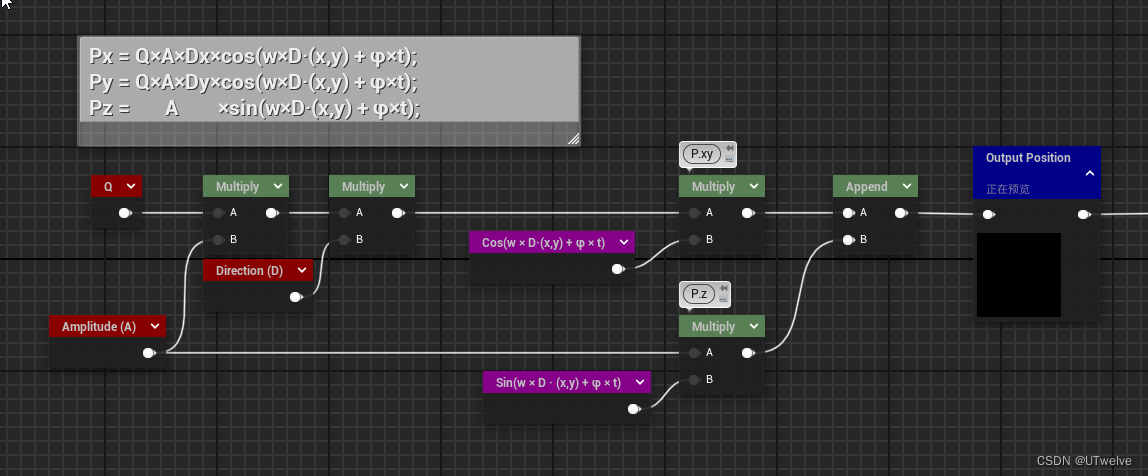
P ( x , y , t ) = ( x + ∑ ( Q i A i × D i . x × cos ( w i D i ⋅ ( x , y ) + φ i t ) ) , y + ∑ ( Q i A i × D i . y × cos ( w i D i ⋅ ( x , y ) + φ i t ) ) , ∑ ( A i sin ( w i D i ⋅ ( x , y ) + φ i t ) ) ) \mathbf{P}\left(x, y, t\right) = \left(\begin{array}{l} \begin{alignedat}{3} &x&+&\sum \left(Q_{i}A_{i} \times \mathbf{D}_{i}.x \times \cos\left(w_{i}\mathbf{D}_{i} \cdot (x, y) + \varphi_{i}t\right)\right),\\ &y&+& \sum \left(Q_{i}A_{i} \times \mathbf{D}_{i}.y \times \cos\left(w_{i}\mathbf{D}_{i} \cdot (x, y) + \varphi_{i}t\right)\right),\\ & & &\sum \left(A_{i} \sin\left(w_{i}\mathbf{D}_{i} \cdot (x, y) + \varphi_{i}t\right)\right) \end{alignedat} \end{array}\right) P(x,y,t)= xy++∑(QiAi×Di.x×cos(wiDi⋅(x,y)+φit)),∑(QiAi×Di.y×cos(wiDi⋅(x,y)+φit)),∑(Aisin(wiDi⋅(x,y)+φit))
∑为求和,∑( )也就是所有波加在一起,然后再在xy通道分别加x和y。
这里我们想要先实现一个波,也就是∑( )的内容,那么公式可以写为:Px = Q×A×Dx×cos(w×D·(x,y) + φ×t); Py = Q×A×Dy×cos(w×D·(x,y) + φ×t); Pz = A ×sin(w×D·(x,y) + φ×t);能看到我们想实现这个公式还需要两个变量, x y xy xy 和 t t t,他们分别是:
公式中的 Q i Q_i Qi 是一个控制波浪陡峭程度的参数。
对于单个波浪 i i i, Q i = 0 Q_i=0 Qi=0 产生常见的滚动正弦波,而 Q i = 1 w i A i Q_i = \frac{1}{w_i A_i} Qi=wiAi1 产生尖锐的波峰。应避免使用较大的 Q i Q_i Qi 值,因为它们会在波峰上方形成"环\卷"。
实际上,我们可以将 Q Q Q 作为“陡峭程度”参数留给制作艺术家来指定,允许范围是 0 0 0 到 1 1 1,并使用 Q i = Q w i A i × numWaves Q_i = \frac{Q}{w_i A_i \times \text{numWaves}} Qi=wiAi×numWavesQ 来变化,从完全平滑的波浪到我们能产生的最尖锐的波浪。
Q的计算为:
其中 n u m W a v e s numWaves numWaves 为波的总数,例如水面由3个GerstnerWaves组合,这里就是3
Steepness变量就是文中说的"陡峭程度"参数
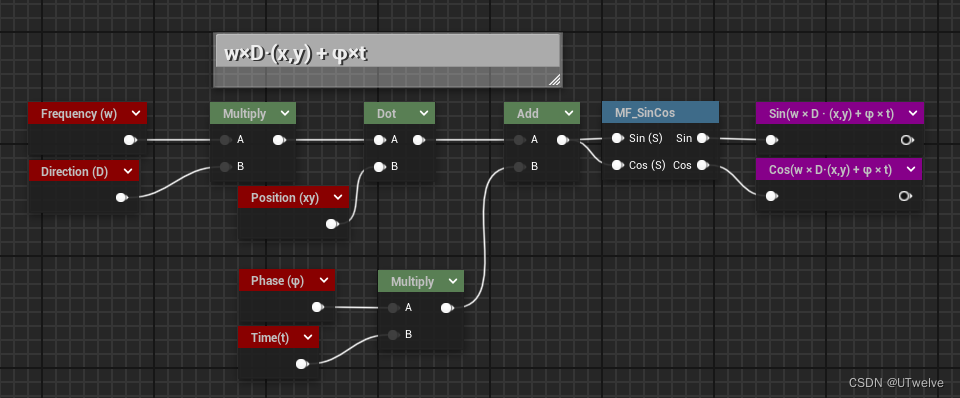
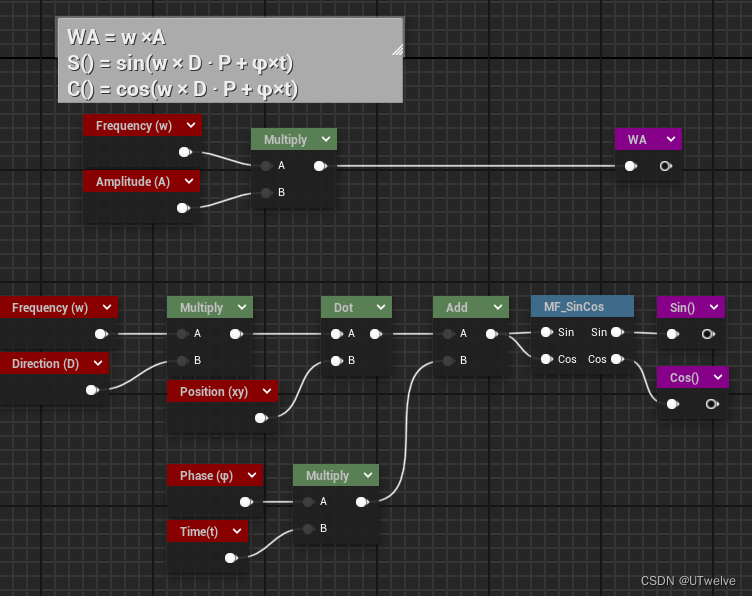
可以看到公式里的( w × D ⋅ ( x , y ) + φ × t w×D·(x,y) + φ×t w×D⋅(x,y)+φ×t )是重复的,我们先把他的SinCos算出来
(这不会影响着色器复杂度,只会让我的截图好看,避免意大利面)
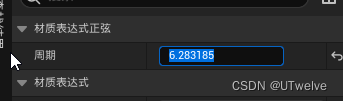
注意这里的 s i n sin sin 和 c o s cos cos 的周期为 2 p i 2pi 2pi
现在我们可以计算公式了
这就是顶点位移的结果,接下来我们计算法线
值得注意的是,公式3和公式9之间唯一的区别是顶点的横向移动。他们的高度是相同的。这意味着我们不再有一个严格的高度函数。即, P ( x , y , t ) . x ≠ x \mathbf{P}(x,y,t).x \neq x P(x,y,t).x=x 。然而,该函数仍然容易求导,并且有一些项可以方便的消去。
其中:
W A = w i × A i , WA=w_{i}\times A_{i}, WA=wi×Ai,
S ( ) = sin ( w i × D i ⋅ P + φ i t ) S()=\sin\left(w_{i}\times\mathbf{D}_{i}\cdot\mathbf{P}+\varphi_{i}t\right) S()=sin(wi×Di⋅P+φit)
C ( ) = cos ( w i × D i ⋅ P + φ i t ) C()=\cos\bigl(w_{i}\times\mathbf{D}_{i}\cdot\mathbf{P}+\varphi_{i}t\bigr) C()=cos(wi×Di⋅P+φit)
又一个万人坑,这里的 P P P 实际上指的是 ( x x x, y y y )
S ( ) S() S() 和 C ( ) C() C() 我在蓝图里写成了 S i n ( ) Sin() Sin() 和 C o s ( ) Cos() Cos()
求导后得到切线空间的基础向量是:
Equation 10 公式10
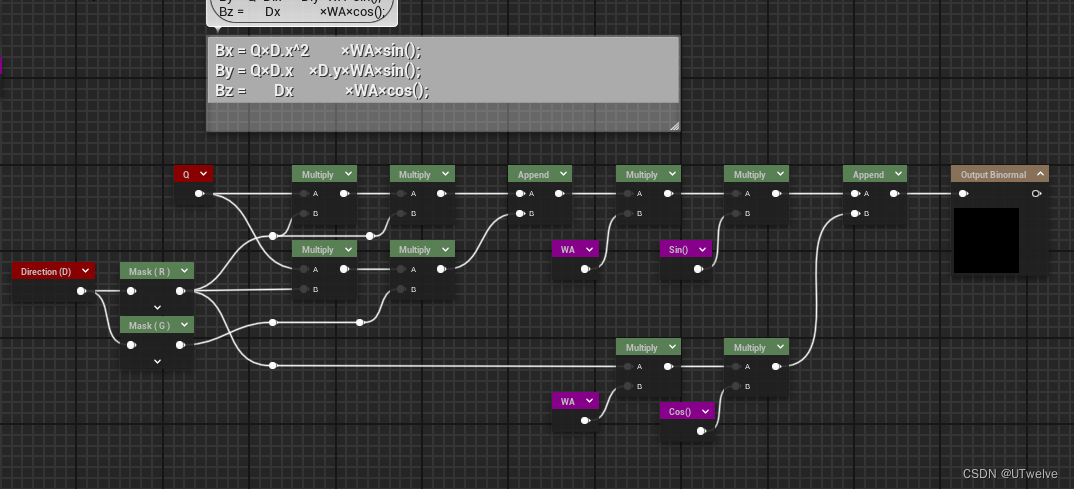
B = ( 1 − ∑ ( Q i × D i . x 2 × W A × S ( ) ) , − ∑ ( Q i × D i . x × D i . y × W A × S ( ) ) , ∑ ( D i . x × W A × C ( ) ) ) \mathbf{B} = \begin{pmatrix} \begin{alignedat}{3} &1&-&\sum\left(Q_i \times \mathbf{D}_i.x^2 \times WA \times S()\right),\\ & &-&\sum\left(Q_i \times \mathbf{D}_i.x \times \mathbf{D}_i.y \times WA \times S()\right),\\ & & &\sum\left(\mathbf{D}_i.x \times WA \times C()\right) \end{alignedat} \end{pmatrix} B= 1−−∑(Qi×Di.x2×WA×S()),∑(Qi×Di.x×Di.y×WA×S()),∑(Di.x×WA×C())
Binormal计算可以写公式为:(注意这里仍然先实现一个波,因此计算公式的∑的内容)
Bx = Q×D.x^2 ×WA×sin(); By = Q×D.x ×D.y×WA×sin(); Bz = Dx ×WA×cos();
Equation 11 公式11
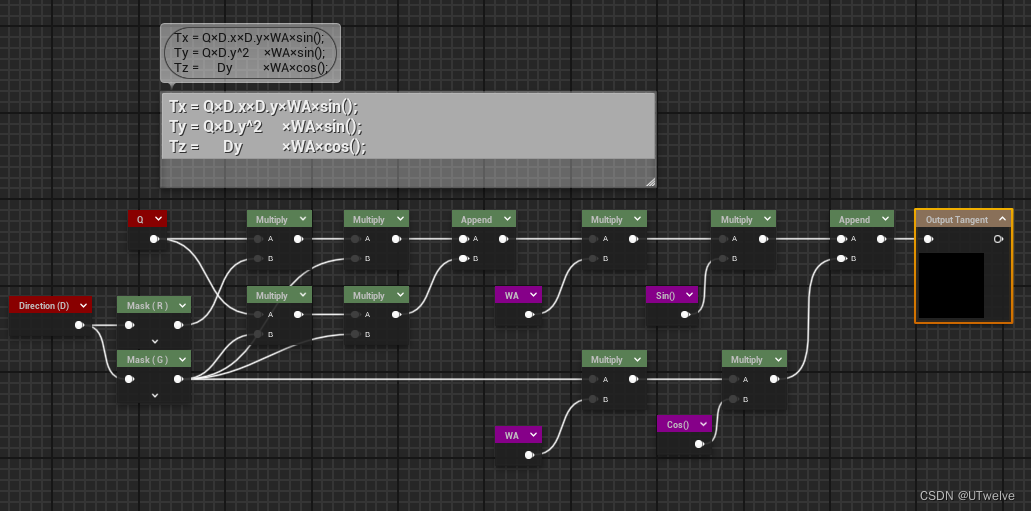
T = ( − ∑ ( Q i × D i . x × D i . y × W A × S ( ) ) , 1 − ∑ ( Q i × D i . y 2 × W A × S ( ) ) , ∑ ( D i . y × W A × C ( ) ) ) \mathbf{T}= \begin{pmatrix} \begin{alignedat}{3} & &-&\sum\bigl(Q_{i}\times\mathbf{D}_{i}.x\times\mathbf{D}_{i}.y\times WA\times S()\bigr),\\ &1&-&\sum\bigl(Q_{i}\times\mathbf{D}_{i}.y^{2}\times WA\times S()\bigr),\\ & & &\sum\bigl(\mathbf{D}_{i}.y\times WA\times C()\bigr) \end{alignedat} \end{pmatrix} T= 1−−∑(Qi×Di.x×Di.y×WA×S()),∑(Qi×Di.y2×WA×S()),∑(Di.y×WA×C())
Tangent:
Tx = Q×D.x×D.y×WA×sin(); Ty = Q×D.y^2 ×WA×sin(); Tz = Dy ×WA×cos();
Equation 12 公式12
N = ( − ∑ ( D i . x × W A × C ( ) ) , − ∑ ( D i . y × W A × C ( ) ) , 1 − ∑ ( Q i × W A × S ( ) ) ) \mathbf{N}=\begin{pmatrix} \begin{aligned} &{}- \sum\bigl(\mathbf{D}_i.x\times WA\times C()\bigr),\\ &{}- \sum\bigl(\mathbf{D}_i.y\times WA\times C()\bigr),\\ 1 &{}- \sum\bigl(Q_i\times WA\times S()\bigr) \end{aligned} \end{pmatrix} N= 1−∑(Di.x×WA×C()),−∑(Di.y×WA×C()),−∑(Qi×WA×S())
这是求法线的公式,但我们做多个波时不应直接使用它。当试图直接混合多个法线时,无论你选择何种法线混合算法来近似,其结果总是错误的。
我们应该使用混合多个波后,使用累加的Binormal,Tangent计算数学意义上正确的法线
这里我们先做两个波,以演示如何混合
我们新建一个∑ 函数,来处理波的混合
这里先把所有波的P,B,T相加,(也就是公式中 ∑ ∑ ∑ 的意义)
然后在函数中计算 ∑ ∑ ∑ 之外的,我们刚才没有处理的内容,
我们回过头再看P、B、T三个公式是如何处理 ∑ ∑ ∑ 的
Position
原公式中,P需要为∑P的xy通道分别增加x,y:
但由于虚幻中顶点空间为0,所以并不需要做这个偏移,直接使用相加后的Position
Binormal
newB.x = 1-∑B.x; newB.y = -∑B.y; newB.z = ∑Bz;Tangent
newT.x = -∑T.x; newT.y = 1-∑T.y; newT.z = ∑T.z;法线 N = C r o s s ( B , T ) N=Cross(B,T) N=Cross(B,T),结合上面的计算,函数内容为:
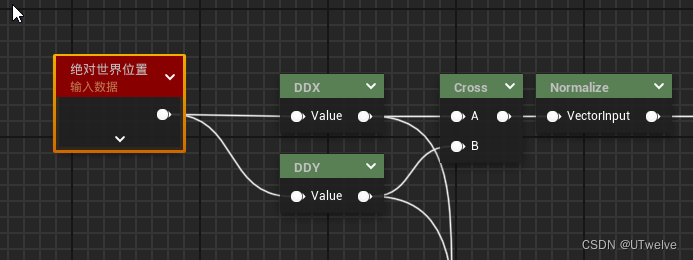
我们先做一个使用DDXDDY实现的顶点法线:
这种做法可以计算出顶点准确的法线,但它受限于模型顶点精度,不能直接用作法线。但是它一个很好的参考,让我们知道正确的法线看上去应该是什么样子
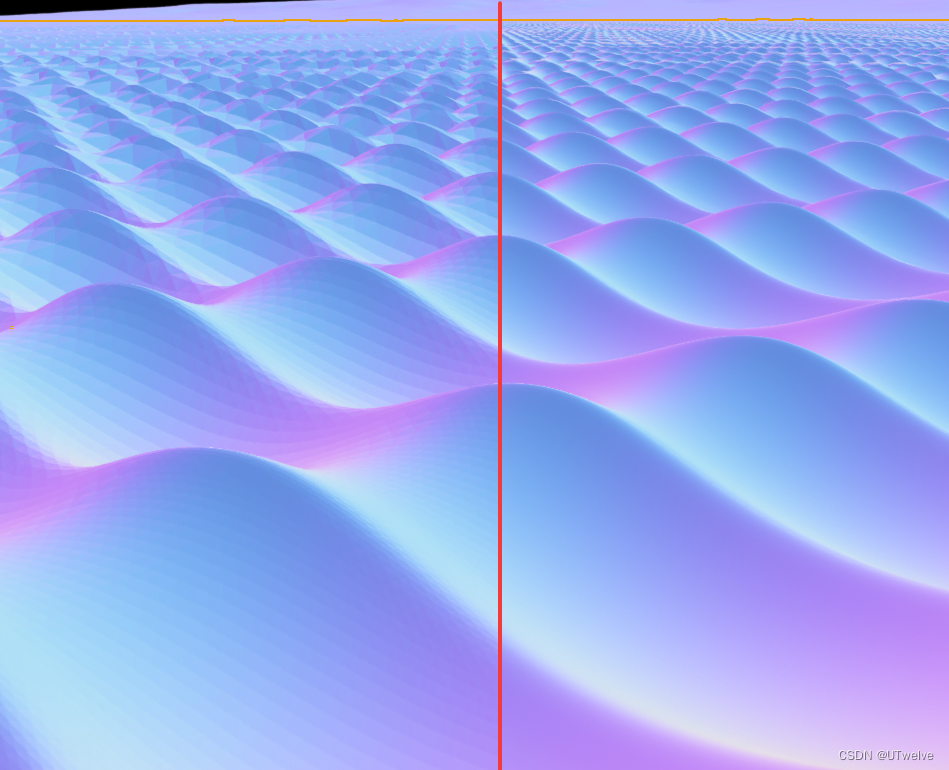
左侧为ddxddy计算的法线,右侧为我们的计算结果,可以看到其结果相一致,我们得到了顶点准确的法线
当我们完成了这些,能注意到,Gerstner Waves函数有一些参数是可以通过物理计算求出.
接下来演示使用真实的物理常数,对算法做一些优化,去掉一些手工的变量,
待续
这些公式不像4b、5b和6b方程那样简洁明了,但它们计算起来非常高效。
在形成波峰环的背景下,仔细观察法线的 z z z 分量证明了这一点非常有趣。虽然 Tessendorf (2001) 从流体动力学的纳维-斯托克斯1描述和“李变换技术2”中推导出他的“切碎效应3”,最终结果是在频率域中表达的格斯特纳波的一个变体。
在频率域中,可以避免并检测到波顶的环形,但在空间域中,我们可以清楚地看到正在发生的事情。
当 Q i × w i × A i Q_i \times w_i \times A_i Qi×wi×Ai 的和大于 1 1 1 时,我们法线的 z z z 分量在峰值处可能变为负值,因为我们的波浪会在自身上方形成环。
只要我们选择的 Q i Q_i Qi 使得这个和始终小于或等于 1 1 1,我们将形成尖锐的峰值但永远不会形成环。
1.2.4参数解释
波长和速度 Wavelength Speed
我们首先选择合适的波长。与其追求现实世界的分布,不如最大化我们能承担的少数波浪的效果。
相似长度的波浪的叠加突出了水面的动态性。
因此,我们选择一个中值波长,并在该长度的一半到两倍之间生成随机波长。中值波长在创作过程中被编写,它可以随时间变化。
例如,在暴风雨期间,波浪可能比晴朗平静时显著更大。
注意,我们不能改变正在活动的波的波长。即便是逐渐改变,波浪的波峰也会向原点扩展或收缩,这看起来非常不自然。
因此,我们改变当前的平均波长,随着时间的推移,当波浪淡出以后,它们将基于新的长度重新生成。方向也是如此。
根据波长,我们可以轻松计算它在表面上的传播速度。Tessendorf 2001中给出忽略高次项的传播关系:
Equation 13 公式13
w = g × 2 π L w=\sqrt{g\times{\frac{2\pi}{L}}} w=g×L2π
其中 w w w 是角频率, g g g 是标准下的(例如980cm/s)重力常数, L L L 是波峰到波峰的长度。
振幅 Amplitude
如何处理振幅是一个见仁见智的问题。
虽然振幅可以看做波长和当前天气条件的函数来求得振幅导数,但我们还是要使用在编写时指定的常数(或脚本化的)比率。
更准确地说,与中值波长一起,艺术家指定了一个中值振幅。
对于任何大小的波浪,其振幅与波长的比率将匹配中值振幅与中值波长的比率。
方向 Direction
波浪行进的方向与其他参数完全独立,因此我们可以根据自己选择的任何标准为每个波浪选择一个方向。
如前所述,我们从大致是风向的恒定向量开始。然后我们从风向的恒定角度内随机选择方向。
这个恒定角度在内容创建时被指定,或者可能被脚本化。
施工中待续
- 参考来自Gerstner Waves圣经—— Mark Finch - Cyan Worlds GPU Gems
Navier-Stokes ↩︎
Lie Transform Technique ↩︎
choppiness ↩︎
相关文章:
虚幻引擎 Gerstner Waves -GPU Gems 从物理模型中实现有效的水体模拟
这篇文章重点在于结合GPU Gems一书中有关Gerstner Waves 的数学公式,在虚幻引擎中复现正确的Gerstner Waves和正确的法线 文中内容整理自书中,并附带我的理解,与在虚幻引擎中的实现,可以参考原文看这篇文章,原文网上很…...

Labview_网络流
网络流的介绍 网络流是一种易于配置、紧密集成的动态通信方法,用于将数据从一个应用程序传输到另一个应用程序,其吞吐量和延迟特性可与 TCP 相媲美。但是,与 TCP 不同的是,网络流直接支持任意数据类型的传输,而无需先…...

让生产管理变简单
随着业务的发展,工厂每天要处理很多订单,还要统筹安排各部门工作以及协调上下游加工企业,生产管理问题也随之而来。 1.销售订单评审困难、无法及时抓取到历史数据做参考。由于数据的不及时性、不准确性无法为正常的生产和采购提供数据支撑。同…...

MySQL与SQLite的区别
MySQL 和 SQLite 是两种常见的关系型数据库管理系统,但它们在设计目标、架构和使用场景上有显著的区别。以下是它们的主要区别: 1. 架构与模式 MySQL: 客户端/服务器模式:MySQL 采用 C/S 架构,数据库服务器运行在一…...
Hi3861 OpenHarmony嵌入式应用入门--LiteOS Event
CMSIS 2.0接口使用事件标志是实时操作系统(RTOS)中一种重要的同步机制。事件标志是一种轻量级的同步原语,用于任务间或中断服务程序(ISR)之间的通信。 每个事件标志对象可以包含多个标志位,通常最多为31个&…...
Centos+Jenkins+Maven+Git 将生成的JAR部署到Jenkins服务器上
背景:前一篇写的是Jenkins和项目应用服务器不在同一个服务器上。但是有的公司可能不会给Jenkins单独弄一个服务器。可能就会出现Jenkins就搭建在某一个应用服务器上。这种情况的参考如下的操作。 1、登录 没有安装的参考下面的安装步骤先安装: Jenkins安装手册 输入账号、…...
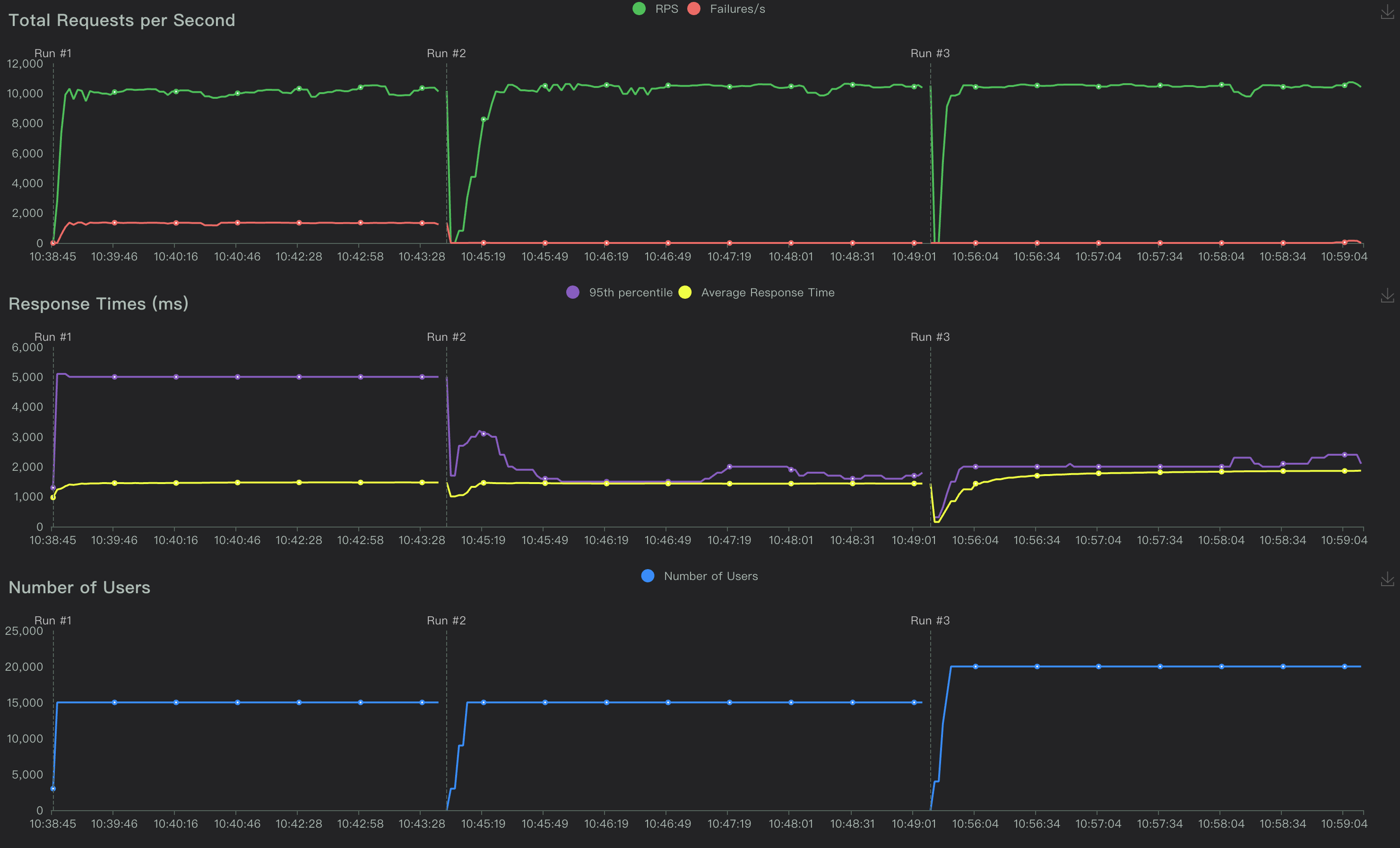
性能评测系列(PT-010):Spring Boot + MySQL,高并发insert
一、测试概述 测试场景 场景编号: PT-010场景描述: Java应用,MySQL单表写测试目的:指定规格、配置、环境下,Java应用数据库简单写场景负载能力评估。(不含调优,所测结果未必是最优结果&#x…...

网站改成HTTPS方法
网站改成HTTPS只要网站没有特殊性的要求,绝大部分网站很轻松的就可以完成,尤其是CMS类似的网站系统或者自助搭建的网站(比如:这种网站可以在网站后台一次性安装并且生效)。 基本要求 将网站改成HTTPS有2个前提&#…...
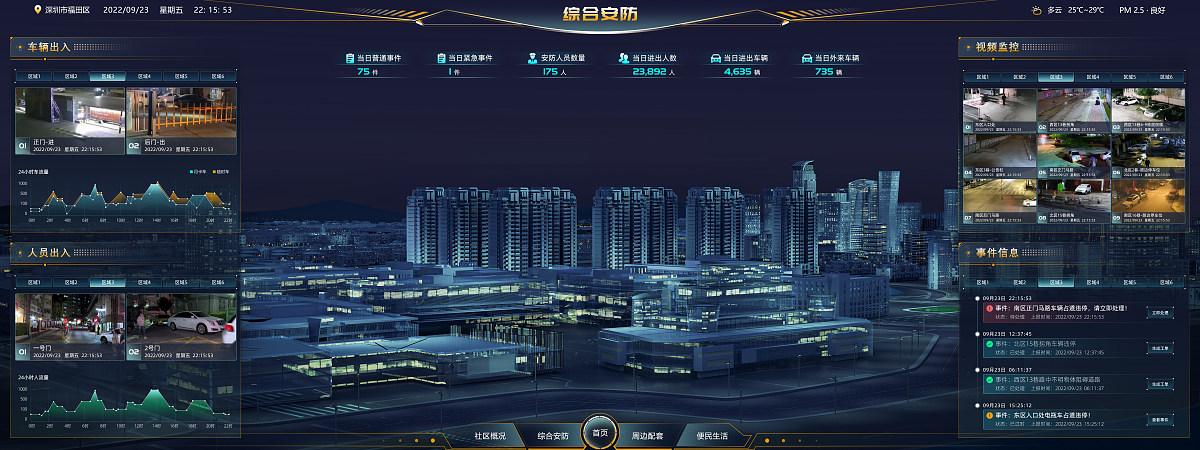
智慧社区:居民幸福生活的保底线,价值非常大。
大屏应该能够显示社区内的关键数据,如人流量、车辆数量、垃圾分类情况等。这些数据可以通过图表、数字、地图等形式展示,以便居民和管理者能够直观地了解社区的情况。 智慧社区可视化大屏成为一个有益于社区管理和居民生活的工具,提供实时、准…...
《昇思25天学习打卡营第1天|NapKinG》
昇思MindSpore 学习昇思大模型的第一天,先了解一下此模型的架构,设计理念,以及层次结构,昇思大模型(MindSpore)的优点有很多,易开发,高效执行,全场景统一部署,是一个全场景深度学习框架 易开发的具体表现为API友好,调试难度低,高效执行包括计算效率,数据预处理效率和分布式训练…...
Java项目毕业设计:基于springboot+vue的幼儿园管理系统
数据库:MYSQL5.7 **应用服务:Tomcat7/Tomcat8 使用框架springbootvue** 项目介绍 管理员;首页、个人中心、用户管理、教师管理、幼儿信息管理、班级信息管理、工作日志管理、会议记录管理、待办事项管理、职工考核管理、请假信息管理、缴费信息管理、幼儿请假管理…...
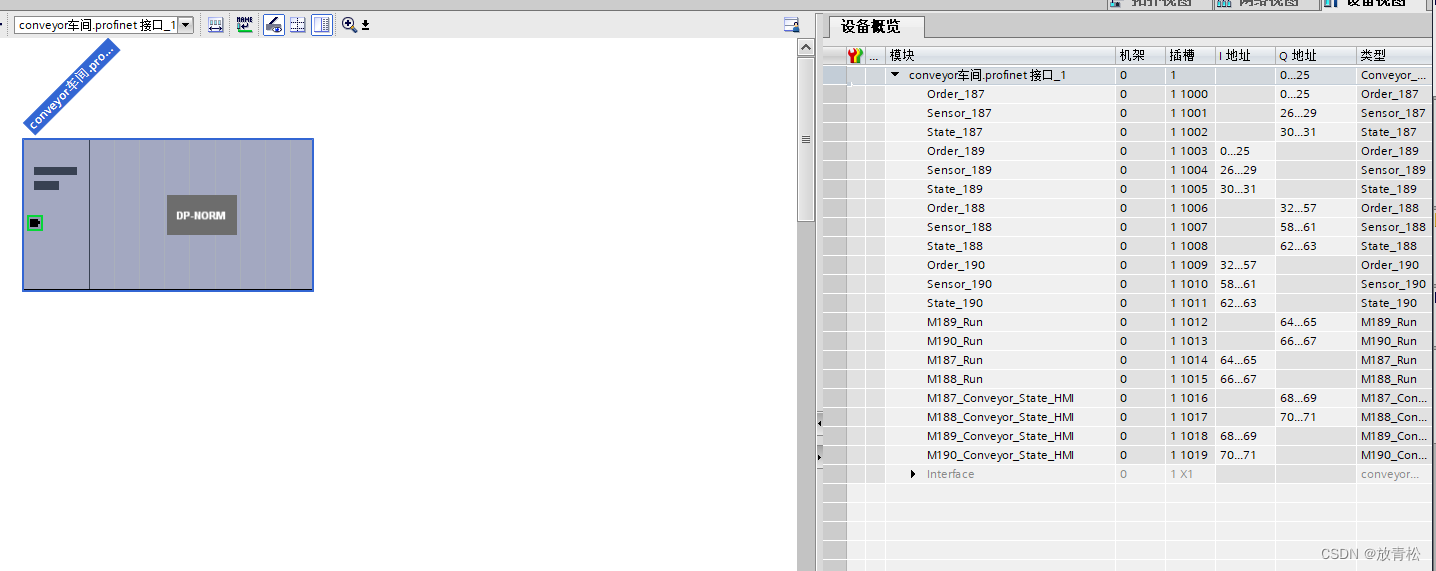
CPU1511作为CPU1513的智能IO设备
一、把一个IO控制器作为另一个IO控制器的IO设备来使用 1、在智能设备通信里定义好传输区后,导出GSD文件 2、在另一个项目程序内添加GSD文件 3、当作PLC的IO设备组态,并连接至PLC_1 4、在右侧更改I区、Q区地址与名称 5、硬件编译并下载,此…...

docker 安装与常用指令
1. docker 安装 sudo yum install -y yum-utilssudo yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.reposudo yum install docker-ce docker-ce-cli containerd.io docker-buildx-plugin docker-compose-pluginsudo systemctl enable do…...

如何将 gz 文件通过 local data 导入 OceanBase?
在很多领域,数据的传输是基于 csv,并且,为了方便,属于同一张表的多个 csv 文件还是打包成 gz 文件进行传输。 当 gz 文件传输到下游时,需要将 gz 中的 csv 数据导入数据库,最直接的方法是: 在…...

electron+vue3+vite
1.创建工程 开源的electron构建脚手架:GitHub - electron-vite/electron-vite-vue: 🥳 Really simple Electron Vite Vue boilerplate. 1.使用命令创建工程(node版本在16上) npm create electron-vite 2.项目目录结构 2.安装依…...

react笔记-04redux篇
redux和react-redux笔记,以及项目中如何使用,对redux的封装,让其使用类似于vuex一样方便。 一、redux 1. redux工作流程 流程:创建action > dispatch分发action > 交给store > reducer加工数据返回给store 2. redux的…...

oracle 等待事件
1.db file scattered read 含义:当一个SQL语句需要从数据文件中读取多块非连续的数据块时,就会发生db file scattered read等待事件。这意味着数据分散在不同的位置,数据库需要进行多次I/O操作来收集所需的信息。场景:这种事件常…...
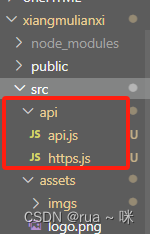
Vue 的 axios二次封装
(以下的接口地址链接换成自己的写!!!) 首先在项目中src的目录下创建一个api的文件夹,在api的文件下在穿件两个文件用于二次封装 别忘了先安装axios:(在根目录下安装axios࿰…...

实验操作步骤:使用Tripwire进行文件完整性监控
摘要 在网络安全领域,文件完整性监控是确保系统安全的关键措施之一。Tripwire作为一个业界领先的文件完整性监控工具,能够帮助系统管理员检测未授权的文件更改。本文将详细介绍如何安装、配置并使用Tripwire进行文件完整性监控的实验操作步骤。 1. Tri…...

使用达梦DMHS平滑迁移Oracle数据到DM8
一、迁移前准备 1.环境描述 服务 IP 架构 Oracle 192.168.10.91/92 RAC、主库 Oracle 192.168.10.98 DG备库 达梦 192.168.10.192/192.168.10.193 主备 DMHS 192.168.10.193(DM端) 192.168.10.98(Oracle端) DTS …...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...