【机器学习】基于Gumbel-Sinkhorn网络的“潜在排列问题”求解
1. 引言
1.1.“潜在排列”问题
本文将深入探索一种特殊的神经网络方法,该方法在处理离散对象时展现出卓越的能力,尤其是针对潜在排列问题的解决方案。在现代机器学习和深度学习的领域中,处理离散数据一直是一个挑战,因为传统的神经网络架构通常是为连续数据设计的。然而,在诸如序列分析、图像识别和自然语言处理等应用中,我们经常会遇到需要处理离散对象的情况。
潜在排列问题是一个典型的例子,它涉及到对一组无序的元素进行重新排列,以找到一种符合某种标准或目标的顺序。这种排列过程在许多实际应用中都是至关重要的,比如排序算法、图像重建和推荐系统等。然而,由于排列空间的大小随着对象数量的增加而急剧增加,直接搜索所有可能的排列通常是不切实际的。
为了解决这个问题,我们提出了一种新型的神经网络架构,它结合了深度学习的强大表示能力和优化技术的精确性。这种网络能够学习从输入数据中提取有用特征,并基于这些特征预测出最优的排列。通过引入一种特殊的网络层,我们能够将排列的搜索过程嵌入到神经网络的训练过程中,从而实现对潜在排列的高效学习和预测。
具体来说,我们的方法利用了一种基于Gumbel-Sinkhorn分布的随机松弛技术,该技术能够将原始的排列问题转化为一个可微分的优化问题。通过这种方式,我们可以使用梯度下降等优化算法来训练神经网络,并直接优化排列的质量。此外,我们还设计了一种新颖的损失函数,用于评估预测排列与实际目标排列之间的差异,从而指导神经网络的训练过程。
在实验中,我们验证了所提出方法的有效性和优越性。通过与其他传统方法和现有神经网络架构的比较,我们发现我们的方法在处理潜在排列问题时具有更高的准确性和效率。此外,我们还探讨了不同参数设置和网络结构对性能的影响,为实际应用提供了有价值的指导。
我们的目标是,在缺乏直接监督的情况下,找到潜在变量的正确排列 P P P。为了实现这一目标,我们将利用Gumbel-Sinkhorn 操作符,该操作符能够将排列 P P P的寻找问题转化为一个线性优化问题。
备注:有关Gumbel-Sinkhorn的论述,请参考[Mena, G., 等人, (2018)]的论文。
1.2.潜在排列问题的数学表达
通常,我们认为神经网络的优势在于它们能够灵活地学习输入和输出之间任意复杂的映射关系。然而,在实际应用中,我们往往可以通过引入特定的归纳偏好来缩小可学习函数的范围,这些偏好基于我们对问题设置的先验知识,是真实且相关的。
一个体现模型设计中归纳偏好重要性的例子是我们对离散对象的操作。例如,想象一下我们有一个数字列表 n \mathbf{n} n,我们希望对其进行排序:通过在神经网络中引入排序的归纳偏好,我们可以更有效地设计模型来学习和执行这一任务。这种设计方法允许模型利用排序操作的组合性质,从而提高学习效率和性能。
n T = [ 5 1 3 4 ] \mathbf{n}^T = \begin{bmatrix}5\\ 1\\ 3\\4\end{bmatrix} nT= 5134
我们可以通过左乘一个排列矩阵 P P P来获得数字的重新排序;
P = [ 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 ] P = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{bmatrix} P= 0001100001000010
将这样的排列矩阵应用到我们的输入中,我们得到:
P n T = [ 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 ] [ 5 1 3 4 ] = [ 1 3 4 5 ] \begin{align} P \mathbf{n}^T &= \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{bmatrix} \begin{bmatrix}5\\ 1\\ 3\\4\end{bmatrix} \\= \begin{bmatrix} 1\\ 3\\4\\5\end{bmatrix} \end{align} PnT= 1345 = 0001100001000010 5134
一种直观的初步思路可能是让我们的神经网络直接学习排列矩阵 P P P。但是,如果我们没有真实的排列矩阵作为监督数据呢?在这种情况下,我们可能会转而优化网络以输出排列后的输入 P n T P\mathbf{n}^T PnT。
然而,我们必须注意到排列矩阵 P P P具有特定的属性。它是一个双随机矩阵的实例,这意味着其行和列的和都等于1。更具体地说,排列矩阵的每一行和每一列都是独热向量,这反映了输入 n T \mathbf{n}^T nT中的每个元素在输出 P n T P\mathbf{n}^T PnT中必须恰好出现一次,且只出现在一个位置上。
那么,我们如何训练网络以学习到这样的双随机矩阵呢?这正是Gumbel-Sinkhorn操作符所要解决的问题!
值得注意的是:排列矩阵是正交矩阵的一个特例。对于这样的矩阵,其逆矩阵就是其转置矩阵。因此,我们有 P T P = I P^T P = \mathbf{I} PTP=I。在后续的处理中,我们可能会用到这个性质。
1.3.Gumbel-Softmax分布**
在介绍Sinkhorn算子之前,我们先回顾一下Gumbel-Softmax分布。Gumbel-Softmax分布是一个可微分的近似,用于从离散分布中采样,这与在变分自编码器(VAE)中使用的重新参数化技巧在处理连续分布时的作用类似。
在VAE中,我们能够通过重新参数化技巧从连续分布中可微分地采样,但直接将这种方法应用于离散分布则不那么直接。
如果我们想要从一个具有类别概率 α = [ α 1 , α 2 , α 3 ] \mathbf{\alpha}=[\alpha_1, \alpha_2, \alpha_3] α=[α1,α2,α3]的类别分布中采样,可以使用Gumbel-Max技巧。这个技巧涉及到计算 log α + G \log \alpha + \mathbf{G} logα+G的 a r g m a x {\rm argmax}
相关文章:

【机器学习】基于Gumbel-Sinkhorn网络的“潜在排列问题”求解
1. 引言 1.1.“潜在排列”问题 本文将深入探索一种特殊的神经网络方法,该方法在处理离散对象时展现出卓越的能力,尤其是针对潜在排列问题的解决方案。在现代机器学习和深度学习的领域中,处理离散数据一直是一个挑战,因为传统的神经网络架构通常是为连续数据设计的。然而,…...

create-react-app创建的项目中设置webpack配置
create-react-app 创建的项目默认使用的是 react-scripts(存在于node_modules文件夹中)来处理开发服务器和构建,它内置了一些webpack相关配置。一般不会暴露出来给开发者,但是在有些情况下我们需要修改下webpack默认配置ÿ…...
【ai】tx2 nx :安装torch、torchvision for yolov5
torchvision 是自己本地构建的验证torchvision nvidia@tx2-nx:~/twork/03_yolov5/torchvision$ nvidia@tx2-nx:~/twork/03_yolov5/torchvision$ python3 Python 3.6.9 (default, Mar 10 2023, 16:46:00) [GCC 8.4.0] on linux Type "help", "copyright",…...

【报错】在终端中输入repo命令后系统未能识别这个命令
1 报错 已经使用curl命令来下载repo工具,但是在终端中输入repo命令后系统未能识别这个命令。 2 分析 通常是因为repo...

【机器学习】K-Means算法详解:从原理到实践
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 K-Means算法详解:从原理到实践引言1. 基本原理1.1 簇与距离度量1.2 …...

解决qiankun项目与子应用样式混乱问题
背景 qiankun项目用的是Vue2Antdesign2,但其中一个子应用用的是Vue3Antdesign4。集成之后发现子应用的样式混乱,渲染的是Antdesign2的样式。 解决 以下步骤在子应用里操作 1. 在main.js引入ConfigProvider ,在app全局注册ConfigProvider …...
黑产当前,如何识别异常图片?
在这个人人都是创作者的年代, UGC 已成为诸多平台的重要组成。 有利益的地方就会有黑产存在, 不少 UGC 平台都被黑产「薅羊毛」搞的心烦意乱, 用户传的图片,怎么就变成视频链接了? 正常运营的平台,为何流量…...

数据模型(models)
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 (1)在App中添加数据模型 在app1的models.py中添加如下代码: from django.db import models # 引入django.…...
743. 网络延迟时间 - Dijkstra算法题解)
【CS.AL】算法核心之贪心算法 —— 力扣(LeetCode)743. 网络延迟时间 - Dijkstra算法题解
文章目录 题目描述References 题目描述 743. 网络延迟时间 - 力扣(LeetCode) 有 N 个网络节点,标记为 1 到 N。 给定一个列表 times,其中 times[i] (u, v, w) 表示有一条从节点 u 到节点 v 的时延为 w 的有向边。 现在…...

25、架构-微服务的驱动力
微服务架构的驱动力可以从多方面探讨,包括灵活性、独立部署、技术异构性、团队效率和系统弹性等。 灵活性和可维护性 灵活性是微服务架构的一个主要优势。通过将单体应用拆分成多个独立的微服务,开发团队可以更容易地管理、维护和更新各个服务。每个微…...
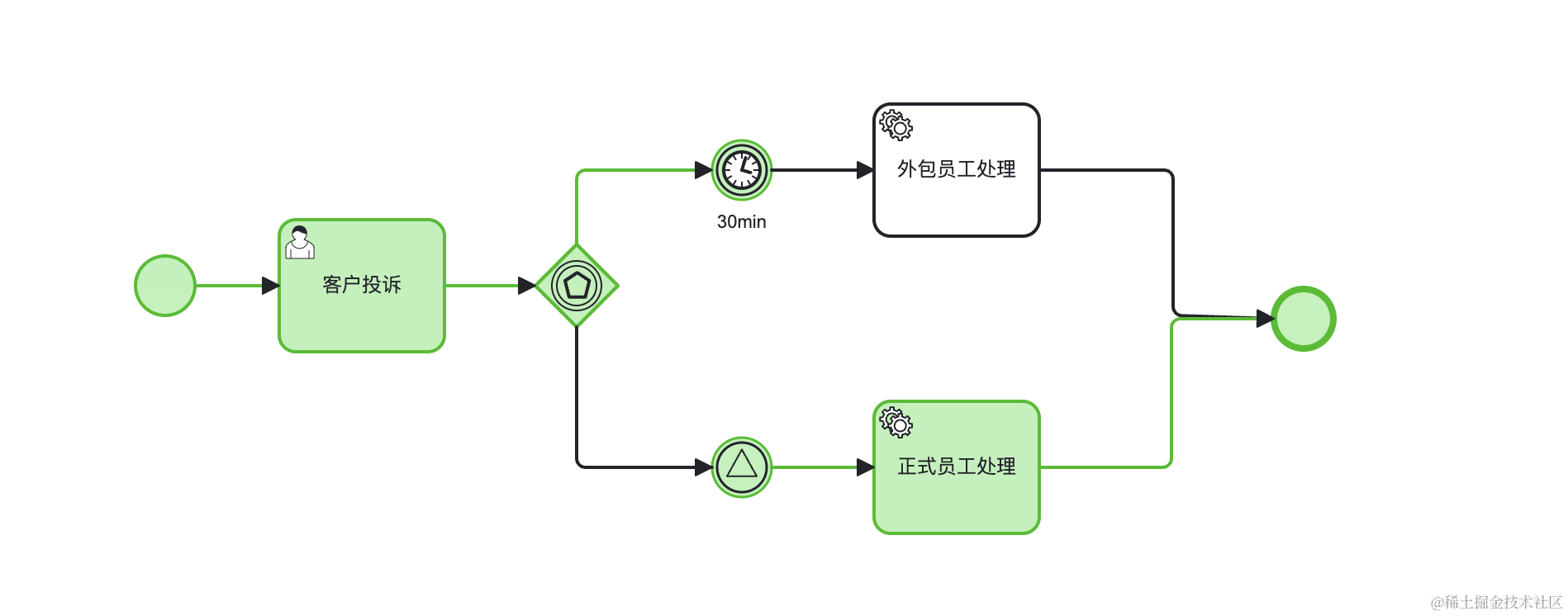
JeecgFlow事件网关概念及案例
事件网关 通常网关基于连线条件决定后续路径,但事件网关有所不同,其基于事件决定后续路径。事件网关的每条外出顺序流都需要连接一个捕获中间事件。 事件网关只有分支行为,流程的走向完全由中间事件决定。可以从多条候选分支中选择事件最先达…...
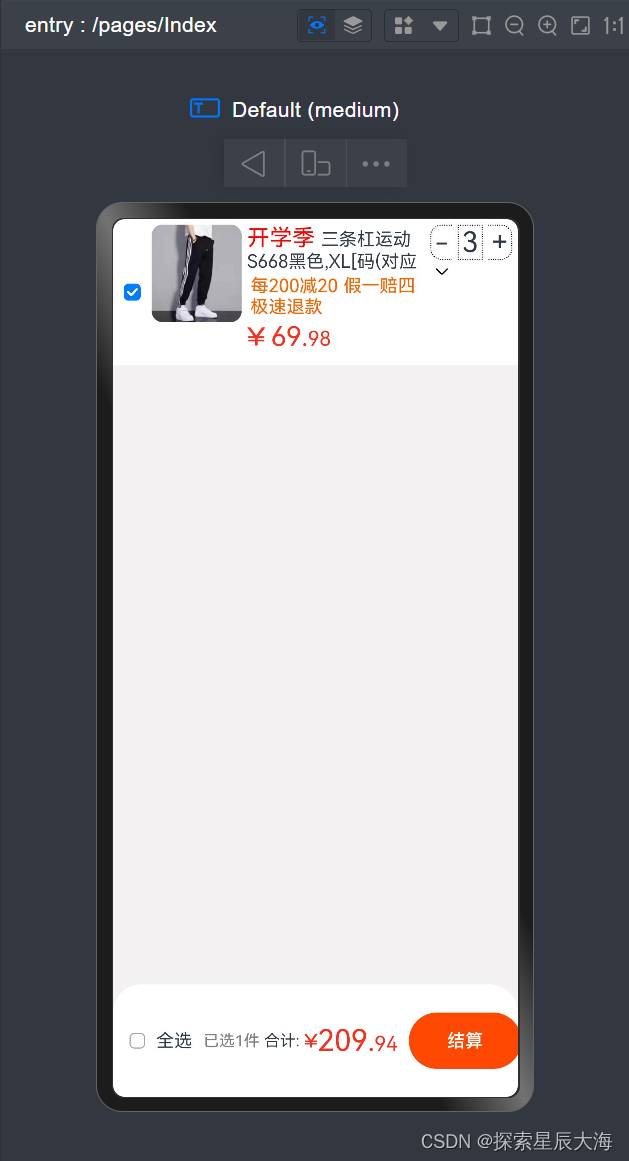
使用鸿蒙HarmonyOs NEXT 开发 快速开发 简单的购物车页面
目录 资源准备:需要准备三张照片:商品图、向下图标、金钱图标 1.显示效果: 2.源码: 资源准备:需要准备三张照片:商品图、向下图标、金钱图标 1.显示效果: 定义了一个购物车页面的布局&#x…...
) 修饰的函数)
iOS 中 attribute((constructor)) 修饰的函数
开发环境声明:此文描述的 attribute((constructor)) 特指使用 Objective-C 开发 iOS、MacOS,Swift 语言不支持这种属性修饰符。 初识 attribute((constructor)) 在 Objective-C 开发中,attribute((constructor)) 是一个 GCC 和 Clang 编译器…...

原生js实现图片预览控件,支持丝滑拖拽,滚轮放缩,放缩聚焦
手撸源代码如下:注释应该很详细了,拿去直用 可以放到在线编辑器测试,记得修改图片路径 菜鸟教程在线编辑器 <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" conten…...

C语言入门课程学习笔记9:指针
C语言入门课程学习笔记9 第41课 - 指针:一种特殊的变量实验-指针的使用小结 第42课 - 深入理解指针与地址实验-指针的类型实验实验小结 第43课 - 指针与数组(上)实验小结 第44课 - 指针与数组(下)实验实验小结 第45课 …...

借助 Cloudflare D1 和 Drizzle 在 Astro 上实现全栈
使用 Cloudflare D1 和 Drizzle ORM 将后端添加到 Astro 项目的分步指南 文章目录 安装 Astro添加 Cloudflare 适配器部署到 Pages安装 wrangler 并登录创建 D1 数据库创建 wrangler.toml 文件将 .wrangler 添加到 .gitignore更新 astro.config.ts安装 Drizzle 依赖项创建 driz…...
SUSE linux 15的网络管理
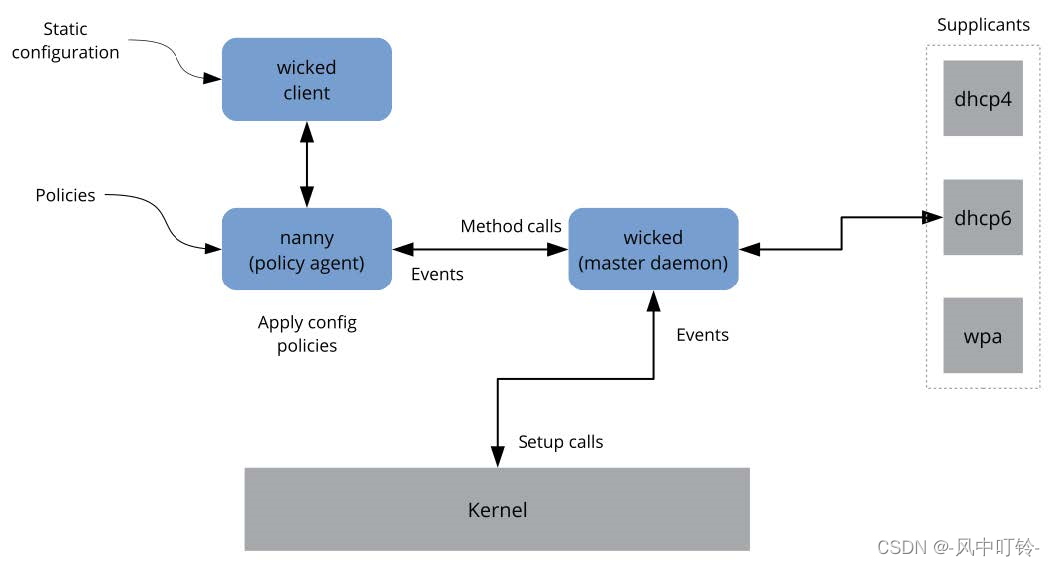
1 手工配置网络 wicked提供了一种新的网络配置框架。自SUSE 12起,SUSE使用了新的网络管理工具wicked,这个是区别与其他常见发行版的。常见的发行版目前大多使用的是NetworkManager服务进行网络管理。 1.1 wicked网络配置 传统网络接口管理面临的挑战之…...

海康威视-下载的录像视频浏览器播放问题
目录 1、播放异常比对 2、视频编码检查 2.1、正常视频解析 2.2、海康视频解析 2.3、比对工具 3、转码 3.1、maven依赖 3.2、实现代码 4、验证 在前面的文章(海康威视-按时间下载录像文件_海康威视 sdk 下载录像 大小0-CSDN博客)中,通…...

养殖自动化管理系统:开启智慧养殖新篇章
在现代农业的快速演进中,养殖业正经历一场前所未有的技术革命。养殖自动化管理系统,作为这场变革的前沿科技,正逐步成为推动行业高效、环保、可持续发展的关键力量。本文将深入探讨自动化养殖系统如何通过精准管理、智能监控、数据驱动决策&a…...
SmartEDA革新来袭:融合Multisim与Proteus精髓,引领电子设计新纪元!
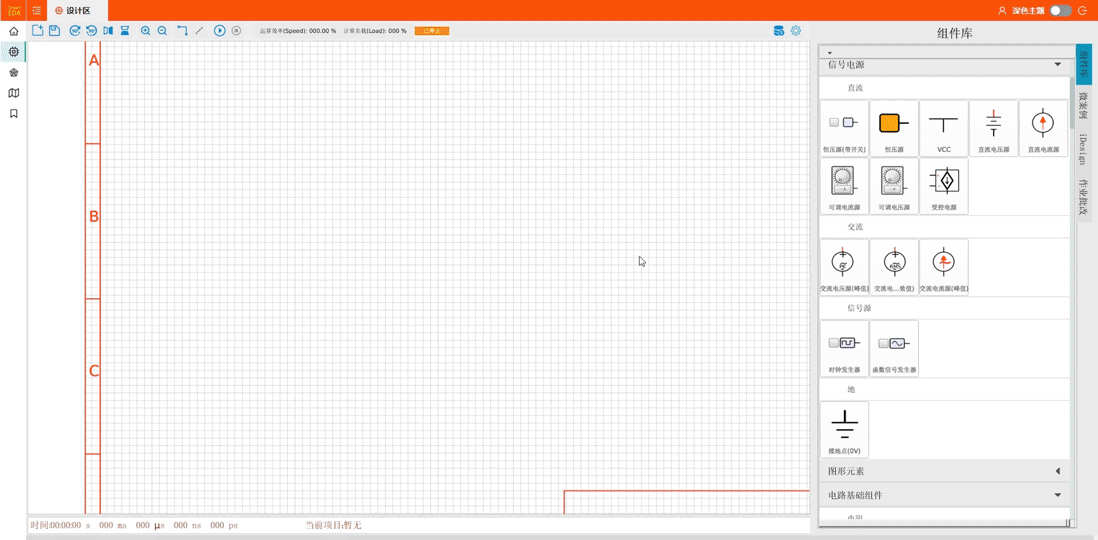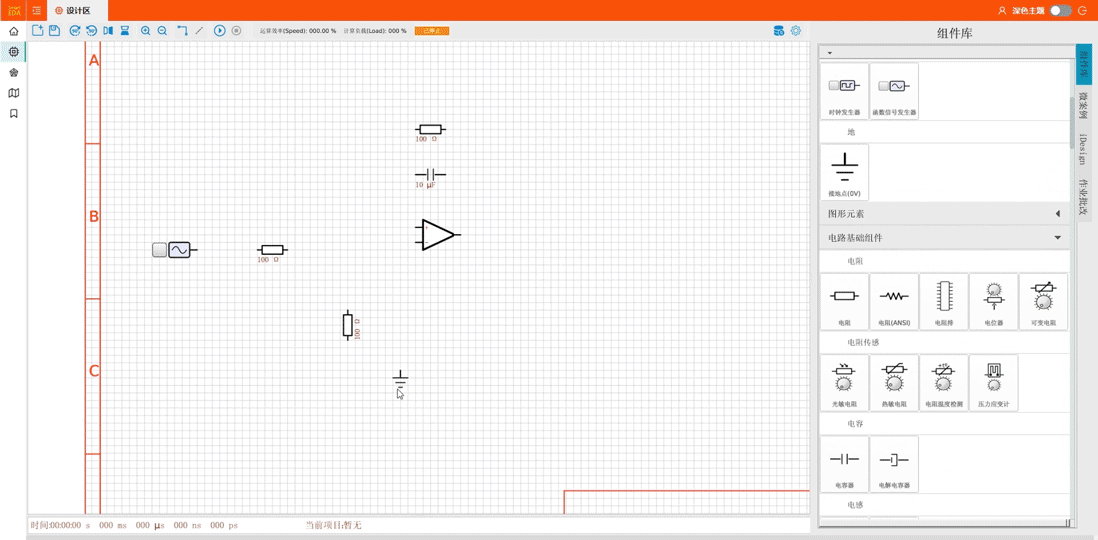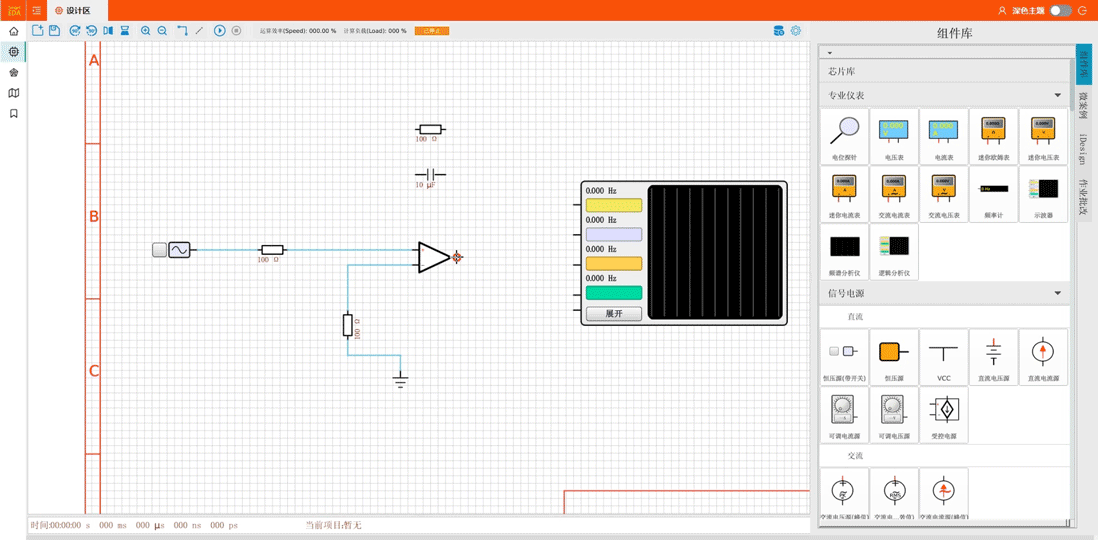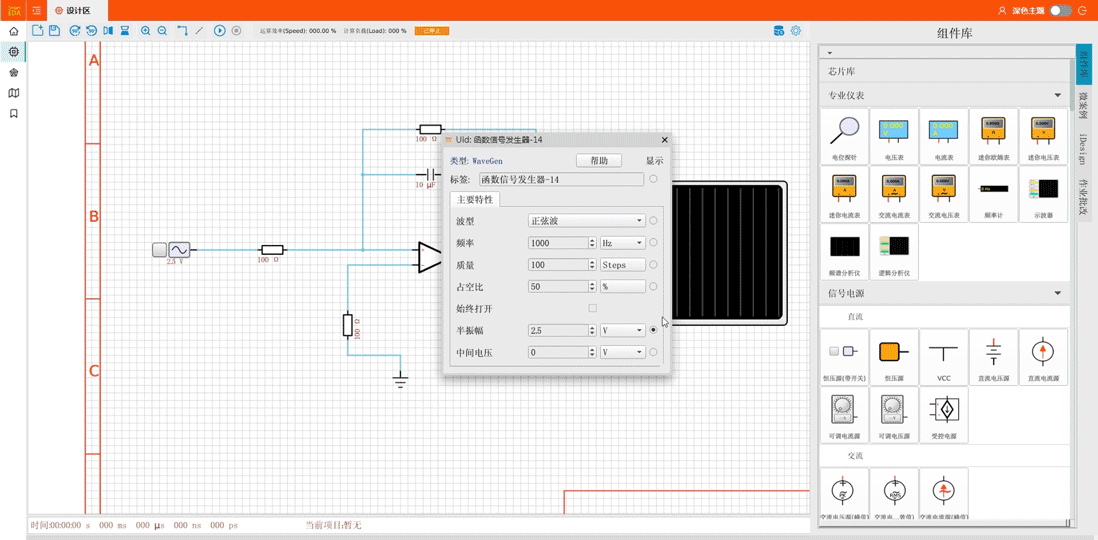
在电子设计领域,每一次技术的革新都如同春风化雨,滋润着设计师们的心田。今天,我们迎来了一个划时代的电子设计自动化(EDA)工具——SmartEDA,它不仅融合了业界知名的Multisim和Proteus的精华,更…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
