算法与数据结构——时间复杂度详解与示例(C#,C++)
文章目录
- 1. 算法与数据结构概述
- 2. 时间复杂度基本概念
- 3. 时间复杂度分析方法
- 4. 不同数据结构的时间复杂度示例
- 5. 如何通过算法优化来提高时间复杂度
- 6. C#中的时间复杂度示例
- 7. 总结

算法与数据结构是计算机科学的核心,它们共同决定了程序的性能和效率。在实际开发中,我们经常需要优化算法以提高程序的运行速度,而时间复杂度是衡量算法性能的重要指标。本文将详细介绍时间复杂度的概念、分析方法以及如何通过算法优化来提高时间复杂度。
1. 算法与数据结构概述
算法是解决问题的步骤,而数据结构则是组织和存储数据的方式。一个高效的算法往往需要配合合适的 data structure 来达到最佳性能。在实际编程中,我们需要根据问题的特点选择合适的算法和数据结构。
2. 时间复杂度基本概念
时间复杂度是衡量算法执行时间与输入规模之间关系的一个概念。通常用大O符号(O-notation)表示,例如O(n)、O(n^2)、O(1)等。时间复杂度可以帮助我们快速评估算法的性能,并在多个算法中进行比较。
3. 时间复杂度分析方法
分析时间复杂度的方法有以下几个步骤:
- 确定算法的基本操作:基本操作通常是算法中出现次数最多的原子操作,其执行时间与输入规模成正比。
- 计算基本操作的执行次数:分析算法流程,计算基本操作在所有可能的输入情况下的执行次数。
- 找出最高次项:在多项式时间内,最高次项决定了算法的时间复杂度。
4. 不同数据结构的时间复杂度示例
数组操作
public void PrintArray(int[] arr)
{for (int i = 0; i < arr.Length; i++){Console.Write(arr[i] + " ");}Console.WriteLine();
}
时间复杂度:O(n),因为循环的执行次数与数组的长度成正比。
链表操作
public class ListNode
{public int val;public ListNode next;
}public void PrintList(ListNode head)
{ListNode current = head;while (current != null){Console.Write(current.val + " ");current = current.next;}Console.WriteLine();
}
时间复杂度:O(n),因为循环的执行次数与链表的长度成正比。
栈和队列:
- 栈的插入/删除操作:O(1)
- 队列的插入/删除操作:O(1)
- 队列的访问操作:O(n)(需遍历)
5. 如何通过算法优化来提高时间复杂度
- 选择合适的算法:针对不同的问题,选择最适合的算法可以显著提高时间复杂度。
- 优化数据结构:使用合适的数据结构可以降低算法的时间复杂度。
- 减少重复计算:避免在算法中重复计算相同的结果,可以减少时间复杂度。
- 剪枝:在算法执行过程中,舍弃一些不必要的分支,可以减少时间复杂度。
示例:快速排序的优化
快速排序的平均时间复杂度为O(n log n),通过优化选择主元素的方式,可以进一步提高其性能。
// 快速排序的优化版本,选取中间元素作为主元素
void quickSort(vector<int>& arr, int left, int right) {if (left >= right) return;int mid = left + (right - left) / 2;int pivot = arr[mid]; // 选择中间元素作为主元素int i = left, j = right;while (i <= j) {while (arr[i] < pivot) i++;while (arr[j] > pivot) j--;if (i <= j) {swap(arr[i], arr[j]);i++;j--;}}quickSort(arr, left, j);quickSort(arr, i, right);
}
6. C#中的时间复杂度示例
O(1)
public int ConstantTimeFunction(int n)
{return n * 2;
}
这个函数的时间复杂度是O(1),因为无论输入规模如何,这个函数的基本操作(乘以2)都只执行一次。
O(n)
public int LinearTimeFunction(int n)
{int sum = 0;for (int i = 0; i < n; i++){sum += i;}return sum;
}
这个函数的时间复杂度是O(n),因为它包含一个循环,其执行次数与输入规模n成正比。
O(n^2)
public int QuadraticTimeFunction(int n)
{int sum = 0;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){sum += i * j;}}return sum;
}
这个函数的时间复杂度是O(n^2),因为它包含两个嵌套的循环,其执行次数与输入规模n的平方成正比。
O(n log n)
public void MergeSort(int[] arr)
{if (arr.Length < 2) return;int mid = arr.Length / 2;MergeSort(arr, 0, mid);MergeSort(arr, mid, arr.Length);Merge(arr, 0, mid, arr.Length);
}private void Merge(int[] arr, int left, int mid, int right)
{// 合并操作
}
归并排序的时间复杂度是O(n log n),因为它的递归分解过程和合并操作的执行次数都与输入规模n的 log(n) 成正比。
7. 总结
掌握时间复杂度的计算和分析方法对于面试和实际编程都非常重要。本文从算法与数据结构概述、时间复杂度基本概念、时间复杂度分析方法、不同数据结构的时间复杂度示例以及如何通过算法优化来提高时间复杂度等方面进行了详细介绍。
相关文章:

算法与数据结构——时间复杂度详解与示例(C#,C++)
文章目录 1. 算法与数据结构概述2. 时间复杂度基本概念3. 时间复杂度分析方法4. 不同数据结构的时间复杂度示例5. 如何通过算法优化来提高时间复杂度6. C#中的时间复杂度示例7. 总结 算法与数据结构是计算机科学的核心,它们共同决定了程序的性能和效率。在实际开发中…...

面试题3:GET 和 POST 有什么区别?
[!]高频面试题。 GET 和 POST 没有本质区别,可以进行相互代替。 1、GET语义:“从服务器获取数据”;POST语义:“往服务器上提交数据”。[设计初衷,不一定要遵守] 2、发请求时,给服务器传递的数据ÿ…...
:模型推理)
探索QCS6490目标检测AI应用开发(三):模型推理
作为《探索QCS6490目标检测AI应用开发》文章,紧接上一期,我们介绍如何在应用程序中介绍如何使用解码后的视频帧结合Yolov8n模型推理。 高通 Qualcomm AI Engine Direct 是一套能够针对高通AI应用加速的软件SDK,更多的内容可以访问:…...

C# 静态类中构造、字段和属性等的执行顺序,含有单例模式分析
C# 静态类时我们实战项目开发中用的非常多的。有些时候可能他的执行顺序并非如我们认为的那样,那就快速来看一下吧! 在C#中,静态类的构造函数是在第一次访问该类的任何成员时执行的。静态构造函数是不可继承的,并且在访问静态类的…...
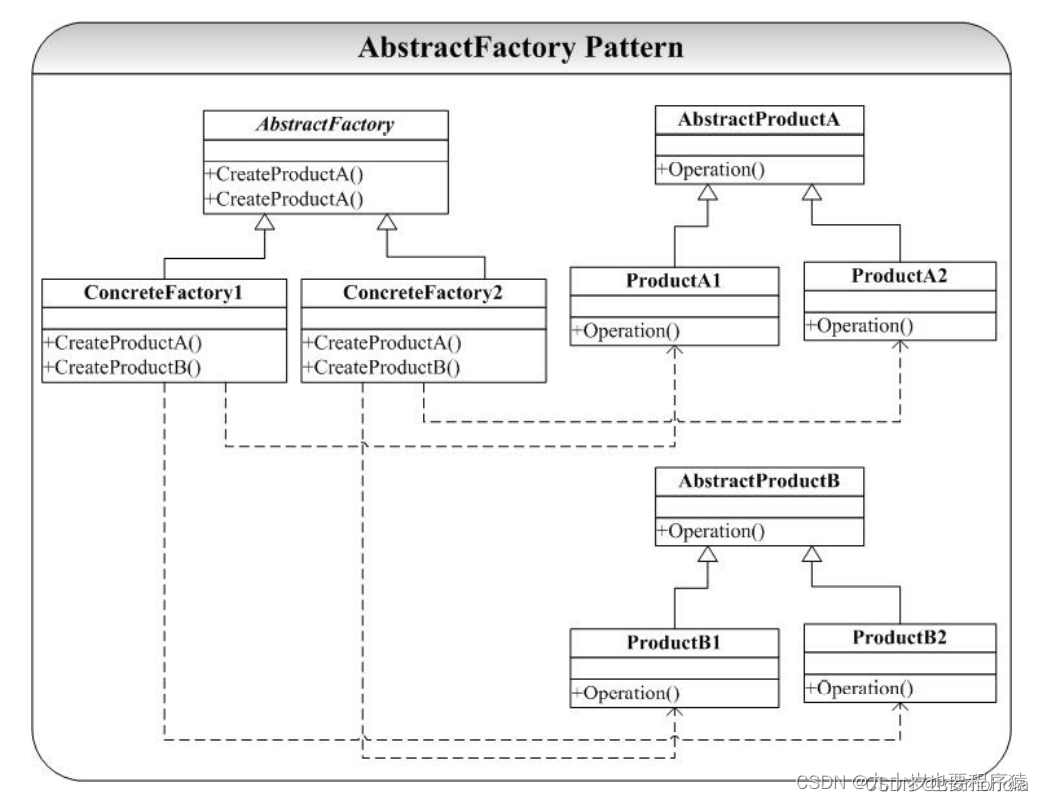
c++设计模式之一创建型模式
1、创建型模式(常见的设计模式) Factory 模式(工厂模式,被实例化的子类) 在面向对象系统设计中经常可以遇到以下的两类问题: 下面是第一类问题和代码示例:我们经常会抽象出一些类的公共接口以…...
上古世纪台服注册账号+下载客户端全方位图文教程
又一款新的MMRPG游戏即将上线啦,游戏名称叫做《上古世纪》游戏采用传统MMO类型游戏的玩法,但是开发商采用了先进的游戏引擎,让玩家们可以享受到极致的视觉体验。同时游戏的背景是建立在大陆分崩离析的基础上。各个部落因为领地的原因纷纷开战…...

【Android】Android中继承Activity、Application和AppCompatActivity的区别
在 Android 开发中,Activity、Application 和 AppCompatActivity 是三个重要的类,它们各自有不同的作用和用途: 1. Activity Activity 是 Android 应用中的一个核心组件,代表了用户界面上的一个单一屏幕或交互界面。每个 Activi…...

SQLite 可以随可执行文件部署在用户机器吗
答案是:可以的。 sqlite 本身就是嵌入式的SQL数据库引擎,不需要单独的服务器进程。sqlite 直接读取和写入普通磁盘文件,sqlite 的整个数据库(所有表、索引、触发器等)都包含在单个磁盘文件中。所以 sqlite 很适合开发…...

大模型的开源不同于传统的开源软件
大模型的开源与传统的开源软件往往有一些不同之处,主要体现在以下几个方面: 数据和许可证的复杂性: 数据依赖性: 大模型通常需要大量的数据来进行训练,这些数据可能来自各种来源,包括公共数据集、专有数据集…...

基于PHP+MySql的留言管理系统的设计与实现
功能概述 网页留言板管理系统,用户层面分为普通用户和管理员,并设权限(即后台留言管理系统普通用户不能访问,别人的留言自己不可以修改删除,未登录不能使用留言功能),功能包括用户登录注册、留…...
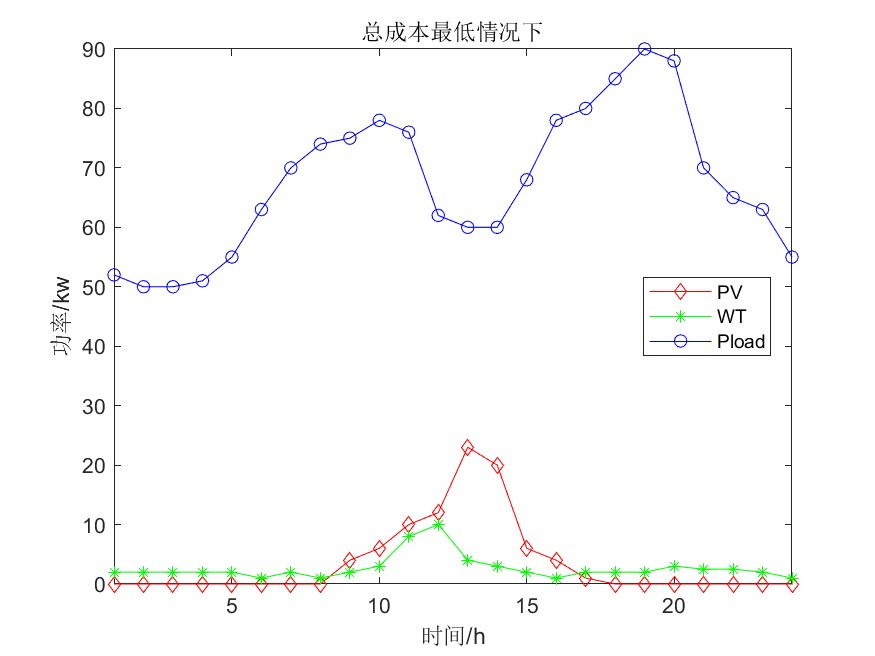
单目标应用:基于吸血水蛭优化器(Blood-Sucking Leech Optimizer,BSLO)的微电网优化(MATLAB代码)
一、微电网模型介绍 微电网多目标优化调度模型简介_vmgpqv-CSDN博客 参考文献: [1]李兴莘,张靖,何宇,等.基于改进粒子群算法的微电网多目标优化调度[J].电力科学与工程, 2021, 37(3):7 二、吸血水蛭优化器求解微电网 2.1算法简介 吸血水蛭优化器(B…...
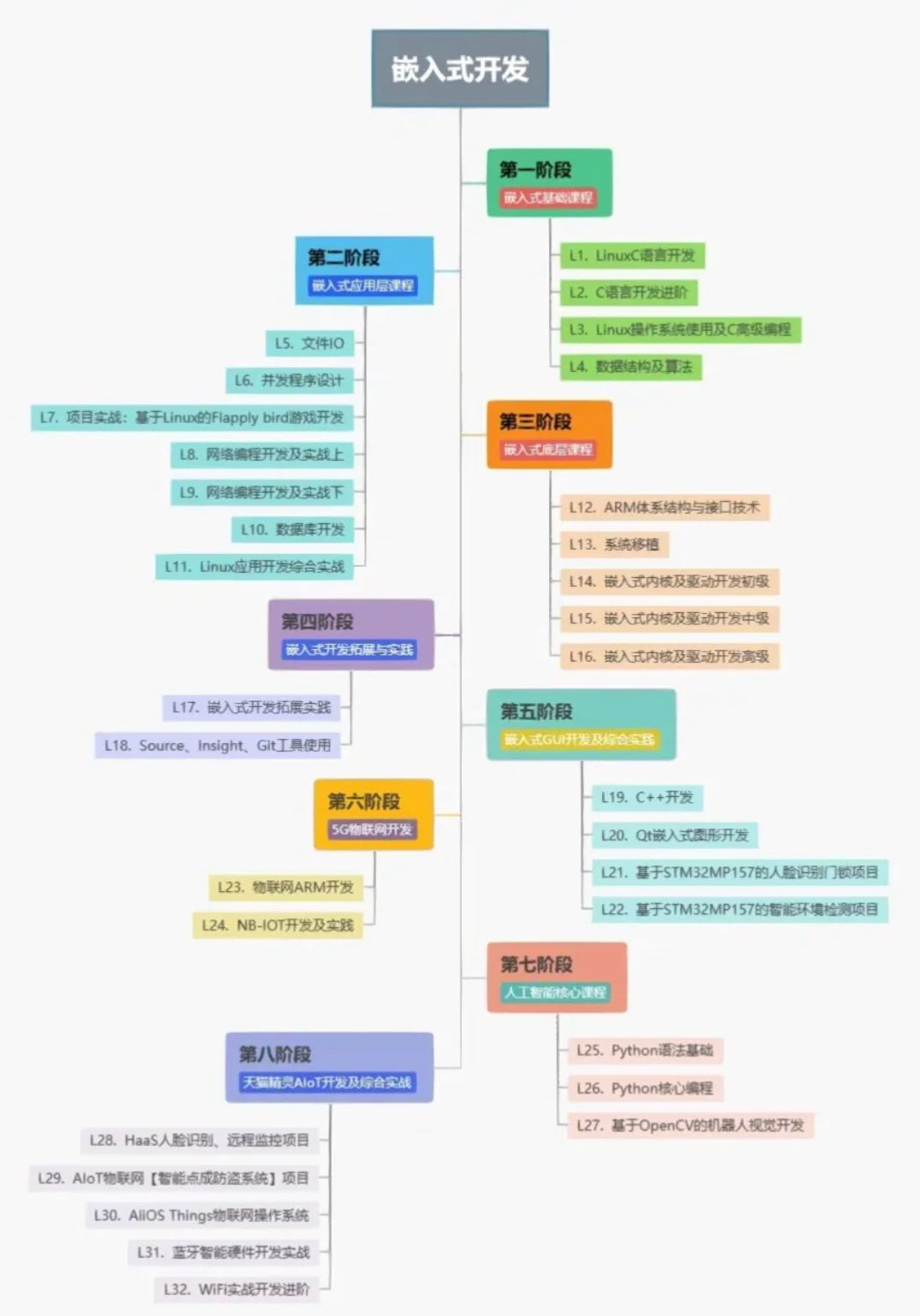
嵌入式工程师从0开始,到底该学什么,怎么学
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「嵌入式的资料从专业入门到高级教程」, 点个关注在评论区回复“666”之后私信回复“666”,全部无偿共享给大家!!!嵌入式是个大筐࿰…...
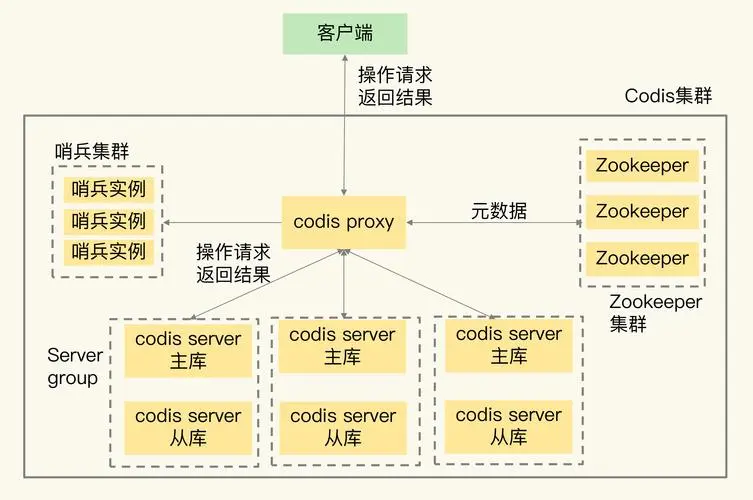
Redis-集群-环境搭建
文章目录 1、清空主从复制和哨兵模式留下的一些文件1.1、删除以rdb后缀名的文件1.2、删除主从复制的配置文件1.3、删除哨兵模式的配置文件 2、appendonly修改回no3、开启daemonize yes4、protect-mode no5、注释掉bind6、制作六个实例的配置文件6.1、制作配置文件redis6379.con…...
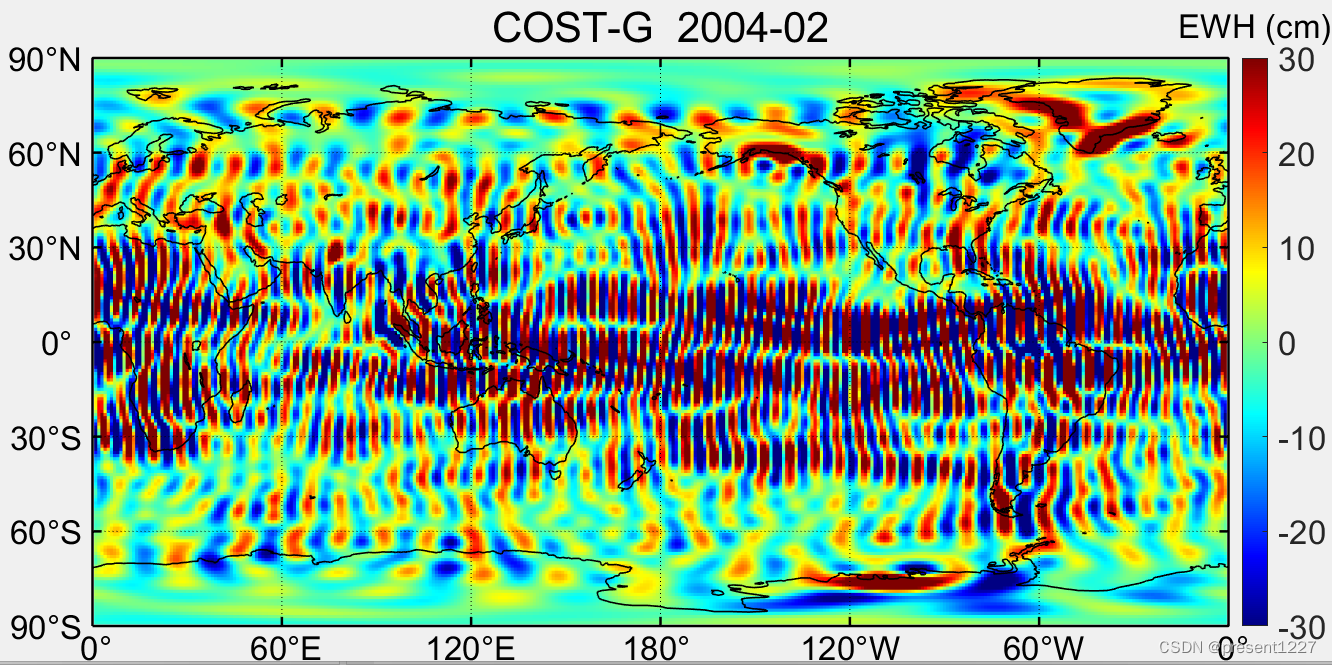
ITSG、COST-G、Tongji和WHU Level-2数据产品读取绘图(Matlab)
数据介绍: ICGEM International Center for Global Gravity Field Models (gfz-potsdam.de) ITSG 2018:Institute of Geodesy at Graz University of Technolog(格拉茨理工大学大地测量研究所) 2018版本,最高60阶球谐…...
-安装libreoffice)
linux(ubuntucentos)-安装libreoffice
因为需要在linux支持word文档和pdf之间的转换,调研验证后选择了libreoffice,在不同的服务器进行了安装,记录如下。 说明: 此处下载版本是7.6.7,如果网址不存在,可以访问http://mirrors.ustc.edu.cn/tdf/l…...
)
上海市计算机学会竞赛平台2023年9月月赛丙组点对之和(一)
题目描述 给定两个数列 𝑎1,𝑎2,…,𝑎𝑛a1,a2,…,an 与 𝑏1,𝑏2,…,𝑏𝑛b1,b2,…,bn,保证这些数字是 11 到 𝑛n 之间的整数,请计算 …...

maven-jar-plugin在springboot中打包成普通引用的jar
如果您想要创建一个不包含Spring Boot特定结构的普通jar包(例如,一个可以被其他项目作为依赖引用的库),您需要在pom.xml中添加maven-jar-plugin的配置。这里是一个示例配置,它将创建一个带有lib分类器的jar包ÿ…...
小型海外仓布局策略:高效利用有限空间,标准化3F流程
合理高效的仓库空间设计,不只是对大型海外仓很关键。对空间有限的小型海外仓来说或许价值更大。 本身仓储空间就有限,如果还没有科学规划,造成空间浪费,那将直接影响到核心业务的运转。 今天我们就给大家整理了对小型海外仓布局…...

【高考志愿】电气工程
目录 一、专业概述 二、专业特点 三、就业前景 四、选择学校 高考志愿选择电气工程是一个极具智慧和远见的决定,因为电气工程在当今社会中扮演着至关重要的角色。以下是对电气工程专业更为详细的解析: 一、专业概述 电气工程及其自动化专业…...

贪吃蛇项目:GameRun与GameEnd部分:游戏的主体运行与善后部分
准备工作:打印得分信息 在进行GameStart之前,我们需要在地图的右侧打印帮助信息,以及目前玩家的得分情况和一个食物在当前速度下的得分情况(加速的状态下按比例增加食物的分数,减速的状态下则相反)…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...
