数据结构——
1. 什么是并查集?
在计算机科学中,并查集(英文:Disjoint-set data structure,直译为不数据结构交集)是一种数据结构,用于处理一些不交集(Disjoint sets,一系列没有重复元素的集合)的合并及查询问题。
举个简单的例子
一个组织里来个10个新人,它们的编号为从1~10,假设此时它们根据彼此的老家而互相亲近(即形成一个小团体),我们要将这10个人划分成不同的小团体,这样划分后形成的结果就是并查集。
接下来我们就来模拟这10个人的划分过程,首先我们可以将每个人的初始值设置为-1,当两个人都属于同一个小团体时,将其中一个人的-1加到另一个人身上,自己的值指向另一个人的下标, 此时另一个人就作为这一个小团体的根,这之后如果有新的人进入这个团体,将新人的-1加到根上,再让新人指向根的下标。这样操作后,所有人中只要自己的值<0,则表明自己是一个团队的根,绝对值表示团队人数,而团体中的其他人均指向这个根。
2. 并查集的常见操作
我们通过上面的模拟,我们可以发现并查集的主要操作主要是:合并,查找根,查看团队个数
我们使用C++实现这个数据结构有
#pragma once
#include <vector>using namespace std;class UnionFindSet
{
public:// 将并查集中的所有元素初始化为-1UnionFindSet(size_t n):_ufs(n, -1){}// 查找根int FindRoot(int x);// 合并void Union(int x1, int x2);// 查看集合个数size_t UnionCount(int x);private:vector<int> _ufs;
};1. 查找根
// 查找根
int FindRoot(int x)
{if (x >= _ufs.size()){throw invalid_argument("无效参数!");return -1;}int root = x;while (_ufs[root] >= 0) // 不为根就向上查找{root = _ufs[root];}return root;
}2. 合并
在合并时,有可能会出现两个团队互相合并的情况,此时我们只需要将其中一个团队的根的值加到另一个团队的根上,再让自己指向另一个团队的根即可,即
// 合并
void Union(int x1, int x2)
{int root1 = FindRoot(x1);int root2 = FindRoot(x2);// 两个人属于不同的集合时,才需要进行合并if (root1 != root2){_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}
}3. 查看集合个数
// 查看集合个数
size_t UnionCount()
{size_t ret = 0;for (auto& e : _ufs){if (e < 0) ret++;}return ret;
}3. 并查集的实际应用
1. 省份数量
题目链接:LCR 116. 省份数量 - 力扣(LeetCode)
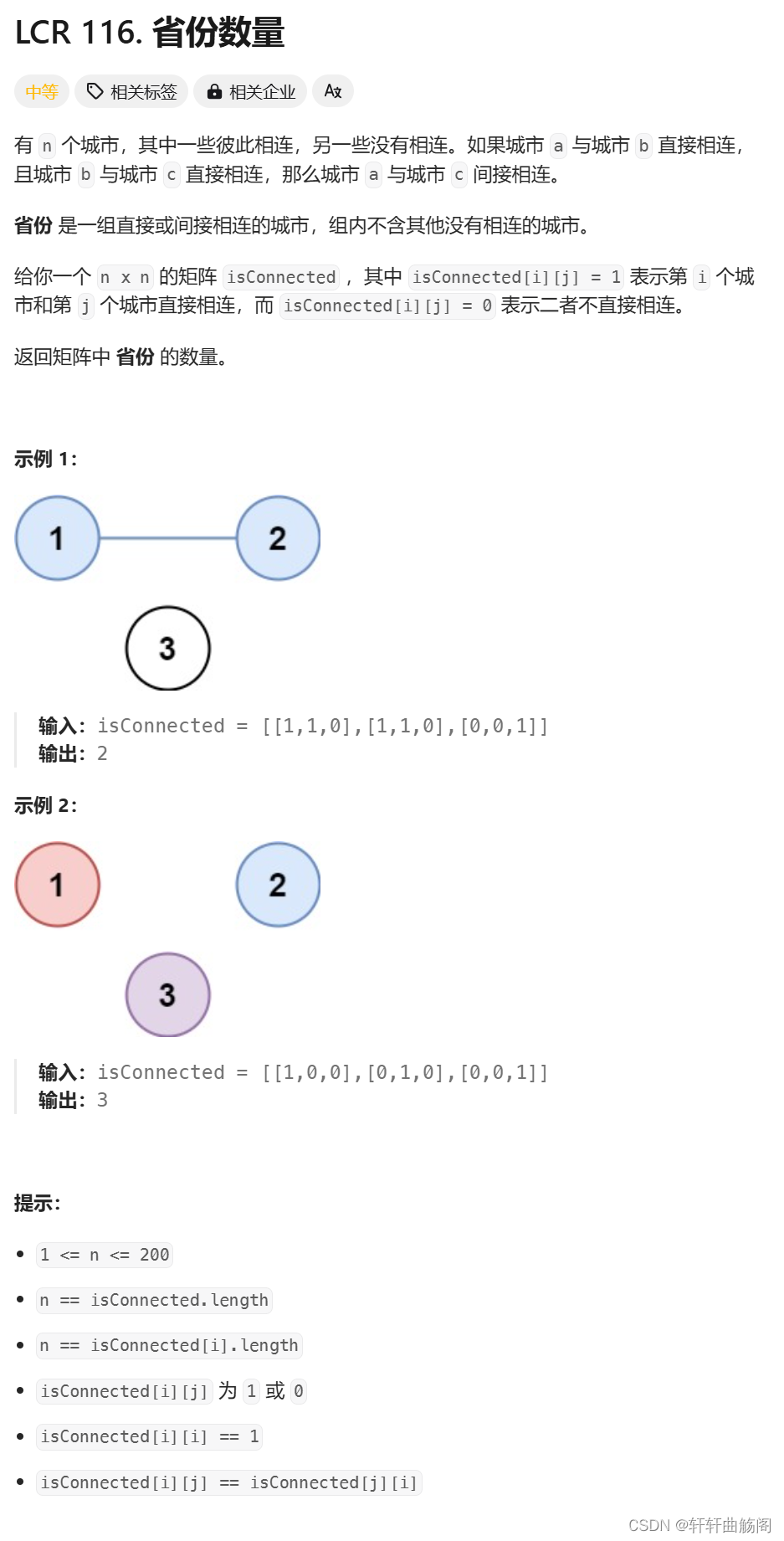
解析:分析题目,如果这道题使用并查集就没有那么难,整体思路就是如果两个城市相连就将他们合并为一个省份,最终返回省份个数即可
解法一:使用并查集数据结构
即
class UnionFindSet
{
public:// 将并查集中的所有元素初始化为-1UnionFindSet(size_t n):_ufs(n, -1){}// 查找根int FindRoot(int x){if (x >= _ufs.size()){throw invalid_argument("无效参数!");return -1;}int root = x;while (_ufs[root] >= 0) // 不为根就向上查找{root = _ufs[root];}return root;}// 合并void Union(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);// 两个人属于不同的集合时,才需要进行合并if (root1 != root2){_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}}// 查看集合个数size_t UnionCount(){size_t ret = 0;for (auto& e : _ufs){if (e < 0) ret++;}return ret;}private:vector<int> _ufs;
};class Solution
{
public:int findCircleNum(vector<vector<int>>& isConnected){UnionFindSet ufs(isConnected.size());for (int i = 0; i < isConnected.size(); i++)for (int j = 0; j < isConnected[i].size(); j++)if (isConnected[i][j] == 1){ufs.Union(i, j);}return ufs.UnionCount();}
};解法二:直接运用并查集思想
即
2. 等式方程的可满足性
题目链接:990. 等式方程的可满足性 - 力扣(LeetCode)

相关文章:

数据结构——
1. 什么是并查集? 在计算机科学中,并查集(英文:Disjoint-set data structure,直译为不数据结构交集)是一种数据结构,用于处理一些不交集(Disjoint sets,一系列没有重复元…...

微信小程序建议录音机
在小程序中实现录音机功能,可以通过使用小程序提供的wx.getRecorderManager() API来获取录音管理对象,然后使用这个对象的start()方法来开始录音,使用stop()方法来停止录音,并使用onStop()方法来监听录音的结束。以下是一个简单的…...

双指针:移动零
题目链接:. - 力扣(LeetCode) 乍一看有点难度,但也是快慢指针的模板。和26. 删除有序数组中的重复项类似,只不过多了一步填充0。 class Solution {public int removeDuplicates(int[] nums) {int fast 1,slow 1;wh…...

图像亮度和对比度的调整
在网上找了很多图像亮度的调整算法,下面是其中一种,可以通过条形框进行调整,并实时的查看对应参数值后的效果。 图像亮度处理公式: y [x - 127.5 * (1 - B)] * k 127.5 * (1 B); x 是输入像素值 y 是输出像素值 B 是亮度值, …...

Linux加固-权限管理_chattr之i和a参数
一、参数i i:如果对文件设置了i属性,不允许对文件进行删除、改名,也不能添加和修改数据;如果对目录设置了i属性,那么只能修改目录下文件的数据,但不允许建立和删除文件。(相当于把文件给锁住了,…...
windows10/win11截图快捷键 和 剪贴板历史记录 快捷键
后知后觉的我今天又学了两招: windows10/win11截图快捷键 按 Windows 徽标键 Shift S。 选择屏幕截图的区域时,桌面将变暗。 默认情况下,选择“矩形模式”。 可以通过在工具栏中选择以下选项之一来更改截图的形状:“矩形模式”…...

上海计算机考研避雷,25考研慎报
上大计算机一直很热 408考研er重来没有让我失望过,现在上大的专业课是11408,按理说,这个专业课的难度是很高的,但是408er给卷出了新高度,大家可以去上大官网看看今年最新的数据,我也帮大家统计了24年最新的…...
第九次作业
BookInfoMapper.xml <?xml version"1.0" encoding"UTF-8"?> <!DOCTYPE mapper PUBLIC "-//mybatis.org//DTD Mapper 3.0//EN" "http://mybatis.org/dtd/mybatis-3-mapper.dtd"> <mapper namespace"com.rabbite…...
A股探底回升,跑出惊天大阳,你们知道为什么吗?
今天的A股,探底回升,让人惊呆了,你们知道是为什么吗?盘面上出现3个重要信号,一起来看看: 1、今天A股市场炸锅了,AI人工智能、国产软件、存储芯片迎来了涨停潮,惊呆了,科技…...
jenkins nginx自动化部署 php项目
在当今快速发展的IT领域,自动化部署已成为提高工作效率和减少错误的关键。Jenkins作为持续集成/持续部署(CI/CD)的佼佼者,结合Docker容器技术和PHP编程语言,以及Ansible自动化工具,可以实现高效、可靠的自动…...
海外代理IP哪个可靠?如何测试代理的稳定性?
在数字化时代,互联网已成为我们日常生活的重要组成部分。然而,随着网络活动的增加,我们面临的安全威胁也随之增加。 黑客攻击、数据泄露、网络钓鱼等安全事件频发,严重威胁着我们的个人隐私和网络安全。代理服务器在当今的互联网世…...
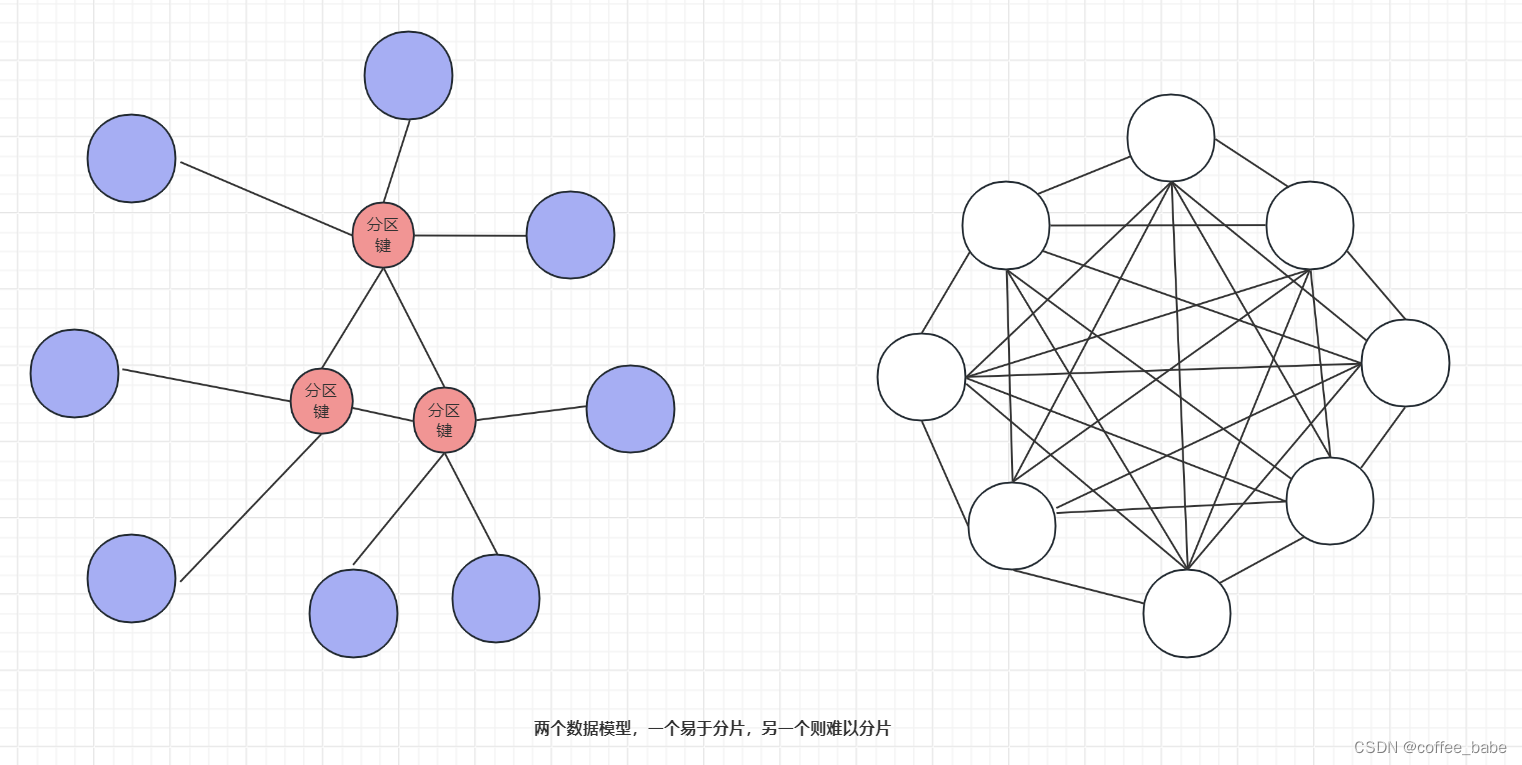
MySQL之可扩展性(四)
可扩展性 向外扩展 分片?还是不分片? 这是一个问题,对吧?答案很简单:如非必要,尽量不分片。首先看是否能通过性能调优或者更好的应用或数据库设计来推迟分片。如果能足够长时间地推迟分片,也许可以直接购买更大地服…...
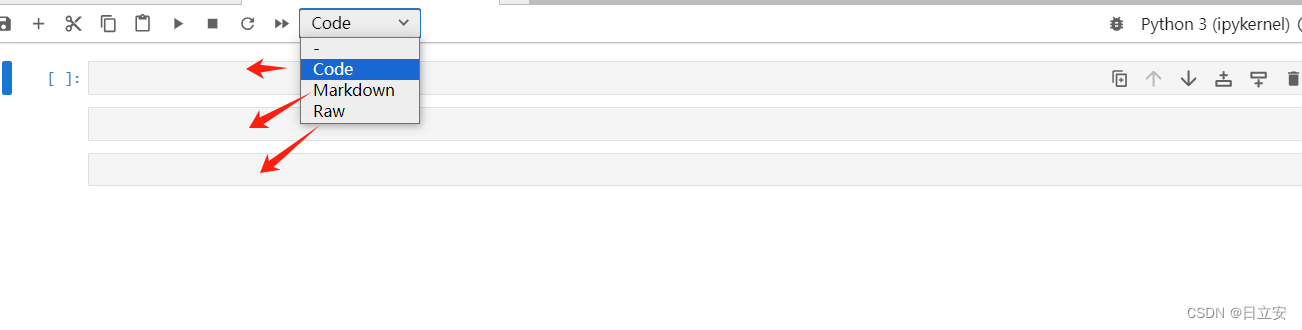
JupyterLab使用指南(三):JupyterLab的Cell详细介绍
JupyterLab Cell 使用教程 JupyterLab 的 cell 是一种强大的工具,提供了编写、执行、展示和记录的全方位支持,使得复杂的计算任务变得简单直观。通过熟练掌握 cell 的各种操作和快捷键,用户可以显著提高工作效率,专注于解决实际问…...
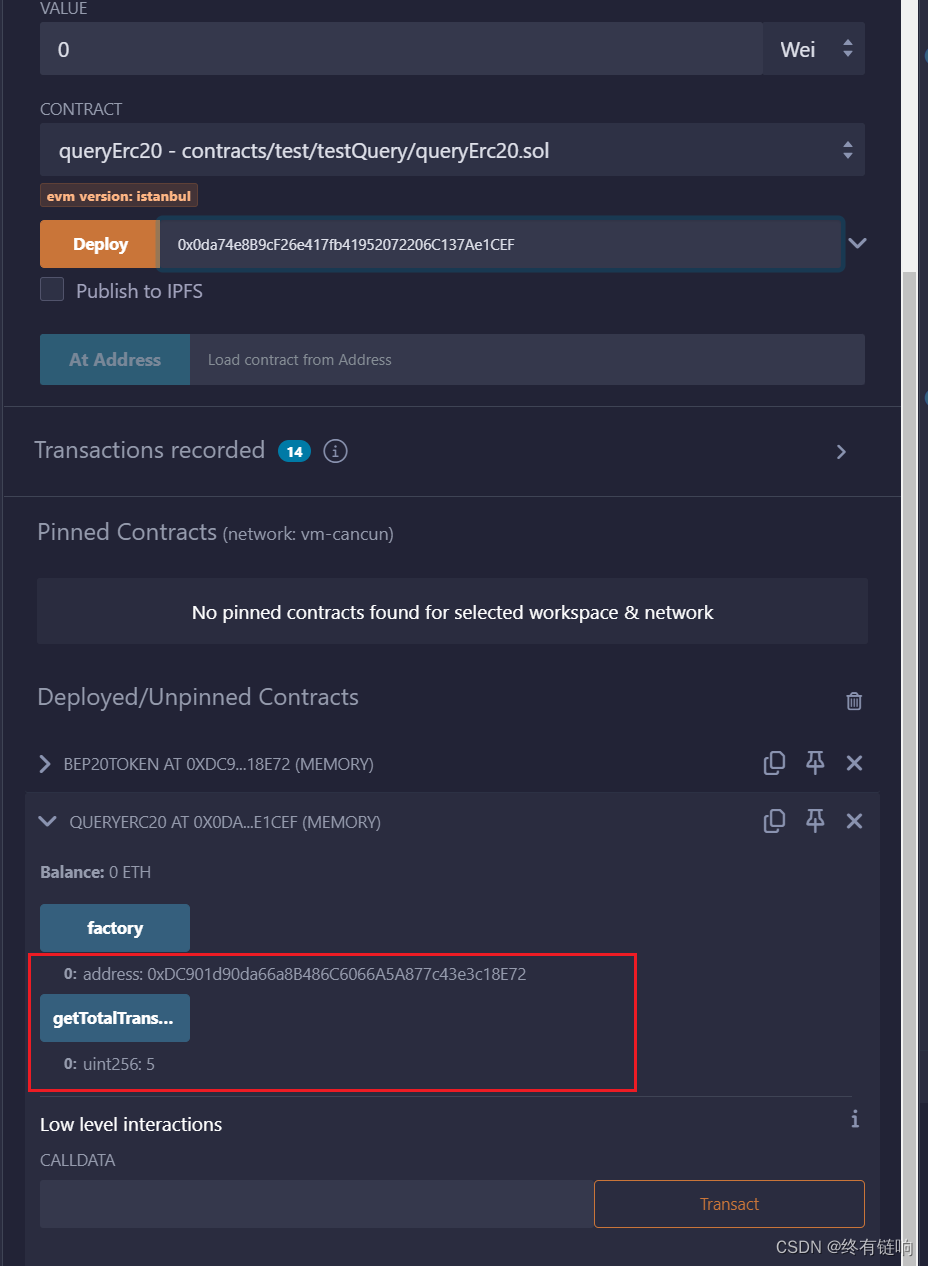
solidity智能合约如何实现跨合约调用函数
背景 比如现在有一个需求、我需要通过外部合约获取BRC20 token的总交易量。那么我需要在brc20的转账函数里面做一些调整,主要是两个函数内统计转移量。然后再提供外部获取函数。 /*** dev Sets amount as the allowance of spender over the callers tokens.** Ret…...

关于Vue2的生命周期会问到哪些面试题?
在Vue2的面试中,关于生命周期的问题通常会涉及以下几个方面: 一、Vue2的生命周期概述 Vue2的生命周期是什么? Vue2的生命周期是指从Vue实例的创建、初始化数据、编译模板、挂载Dom、渲染、更新、卸载等一系列过程。 二、生命周期钩子函数 …...
尚品汇-(七)
(1)在网关中实现跨域 全局配置类实现 包名:com.atguigu.gmall.gateway.config 创建CorsConfig类 Configuration public class CorsConfig {Beanpublic CorsWebFilter corsWebFilter(){// cors跨域配置对象CorsConfiguration configuration…...
【Python datetime模块精讲】:时间旅行者的日志,精准操控日期与时间
文章目录 前言一、datetime模块简介二、常用类和方法三、date类四、time类五、datetime类六、timedelta类七、常用的函数和属性八、代码及其演示 前言 Python的datetime模块提供了日期和时间的类,用于处理日期和时间的算术运算。这个模块包括date、time、datetime和…...
)
keepalived 服务高可用(简约版)
本文基于centos 7记述如何使用keepalived 背景 为生产环境准备一台备机是极其必要的,防止主机宕掉无服务可用的情况出现。但是同一局域网内每台主机都分配了一个唯一IP,这些IP既然相互不同,那么服务请求的时候岂不是要切换IP地址?…...

【前端】Vue项目和微信小程序生成二维码和条形码
前言:哈喽,大家好,我是前端菜鸟的自我修养!今天给大家分享Vue项目和微信小程序如何生成二维码和条形码,介绍了JsBarcode、wxbarcode等插件,并提供具体代码帮助大家深入理解,彻底掌握!…...
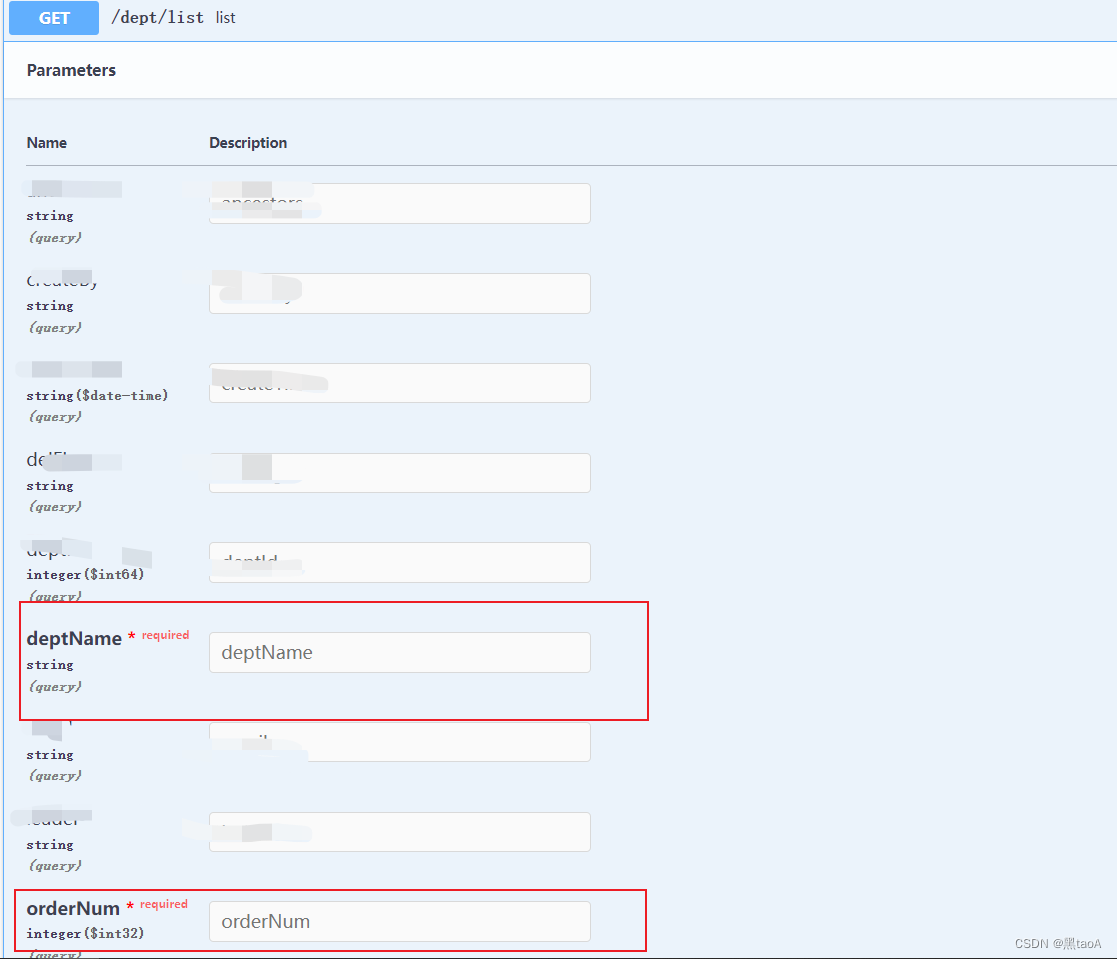
同时使用接口文档swagger和knife4j
项目场景: springboot项目中同时使用接口文档swagger和knife4j 问题描述 在实体类中设置了字段必填的属性,在访问接口文档时出现异常 实体类关键代码片段 /*** 部门表 sys_dept*/ public class SysDept extends BaseEntity {private static final lo…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...
