Studying-代码随想录训练营day21| 669.修建二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树、二叉树总结
第21天,二叉树最后一篇,冲💪
目录
669.修建二叉搜索树
108.将有序数组转换为二叉搜索树
538.把二叉搜索树转换为累加树
二叉树总结
669.修建二叉搜索树
文档讲解:代码随想录修建二叉搜索树
视频讲解:手撕修建二叉搜索树
题目:

学习:
本题需要注意的点很多,不能够轻易的就把节点删除,首先:1.本题给出的最小边界值和最大边界值,不一定会存在树中,只是提供一个区间大小,因此不能够节点判断是否等于low或者high。2.在找到小于low的值后不能够直接将其删除,因为它的右孩子不一定小于low,同理大于high的节点也不能直接删除,还需要关注它的左孩子。3.在2的基础上,也不能直接把右孩子返回,因为右孩子大于low的情况下,右孩子的左孩子还是可能会小于low需要删除,因此还需要不断的进行遍历。(该情况如下图所示,如果区间在[2,3]之间)
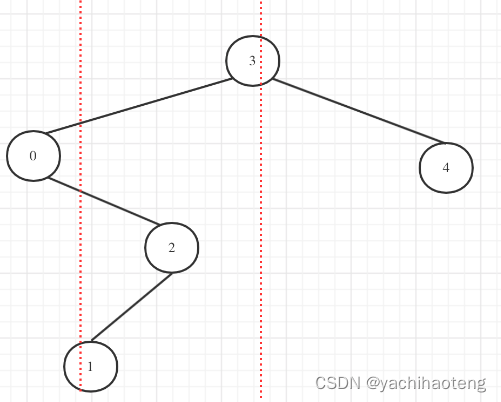
依据上述所说,来设计递归三部曲。
代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public://确定返回值,本题需要重新构造二叉树节点,因此使用返回值更加方便,当然也可以没有返回值就需要手动进行左右孩子构造TreeNode* trimBST(TreeNode* root, int low, int high) {//确定终止条件if (root == nullptr) return nullptr;//确定单层递归逻辑(核心是将root转移到low和high区间内)//1.当前值大于highif (root->val > high) {//在该节点左边找寻是否有合适的值return trimBST(root->left, low, high);}//2.当前值小于lowif (root->val < low) {//在该节点右边找寻是否有合适的值return trimBST(root->right, low, high);}//3.当前值在low和high区间内,但是还不能就此下定义,还需要判断该节点左右孩子是否合格root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);//持续把修改后的节点返回上层return root;}
};代码:本题也能够使用迭代法,且由于二叉搜索树自带遍历条件,因此不需要额外空间。
//时间复杂度O(n)
//空间复杂度O(1)
class Solution {
public:TreeNode* trimBST(TreeNode* root, int L, int R) {if (!root) return nullptr;// 处理头结点,让root移动到[L, R] 范围内,注意是左闭右闭while (root != nullptr && (root->val < L || root->val > R)) {if (root->val < L) root = root->right; // 小于L往右走else root = root->left; // 大于R往左走}TreeNode *cur = root;// 此时root已经在[L, R] 范围内,处理左孩子元素小于L的情况while (cur != nullptr) {while (cur->left && cur->left->val < L) {cur->left = cur->left->right;}cur = cur->left;}cur = root;// 此时root已经在[L, R] 范围内,处理右孩子大于R的情况while (cur != nullptr) {while (cur->right && cur->right->val > R) {cur->right = cur->right->left;}cur = cur->right;}return root;}
};108.将有序数组转换为二叉搜索树
文档讲解:代码随想录将有序数组转换为二叉搜索树
视频讲解:手撕将有序数组转换为二叉搜索树
题目:

学习:
注意本题需要构造的不仅是二叉搜索树还需要是一颗平衡二叉树。平衡二叉树需要所有中间节点的左右孩子的高度差不大于1。
依据上述条件,又因为本题给的数组已经是一个升序排列的数组了,因此本题显然是从中间节点进行构造,每次取数组的中间节点,即可构造出平衡的二叉搜索树。注意如果数组是奇数,显然选中间的节点,如果数组是偶数则中间的两个节点选哪个都可以,只要统一就行,最后构造出的二叉树会有所区别,这也是本题答案不唯一的原因。
代码:
//时间复杂度O(n)
//空间复杂度O(n^2)
class Solution {
public:TreeNode* sortedArrayToBST(vector<int>& nums) {//确定终止条件if(nums.size() == 0) return nullptr;//取中间值int mid = nums.size()/2;TreeNode* node = new TreeNode(nums[mid]);//左区间vector<int> left(nums.begin(), nums.begin() + mid);//右区间vector<int> right(nums.begin() + mid + 1, nums.end());//分配左右子树node->left = sortedArrayToBST(left);node->right = sortedArrayToBST(right);return node;}
};代码:不使用额外空间,下标确定数组区间
//时间复杂度O(n)
//空间复杂度O(n)递归产生的栈空间
class Solution {
public://不使用额外空间,下标法TreeNode* traversal(vector<int>& nums, int left, int right) {//确定终止条件(区间左闭右闭)if(left > right) return nullptr;//找到中间值int mid = left + (right - left)/2; //防止数值越界TreeNode* node = new TreeNode(nums[mid]);//左区间node->left = traversal(nums, left, mid - 1);//右区间node->right = traversal(nums, mid + 1, right);return node;}TreeNode* sortedArrayToBST(vector<int>& nums) {return traversal(nums, 0, nums.size() - 1);}
};538.把二叉搜索树转换为累加树
文档讲解:代码随想录把二叉搜索树转换为累加树
视频讲解:手撕把二叉搜索树转换为累加树
题目:
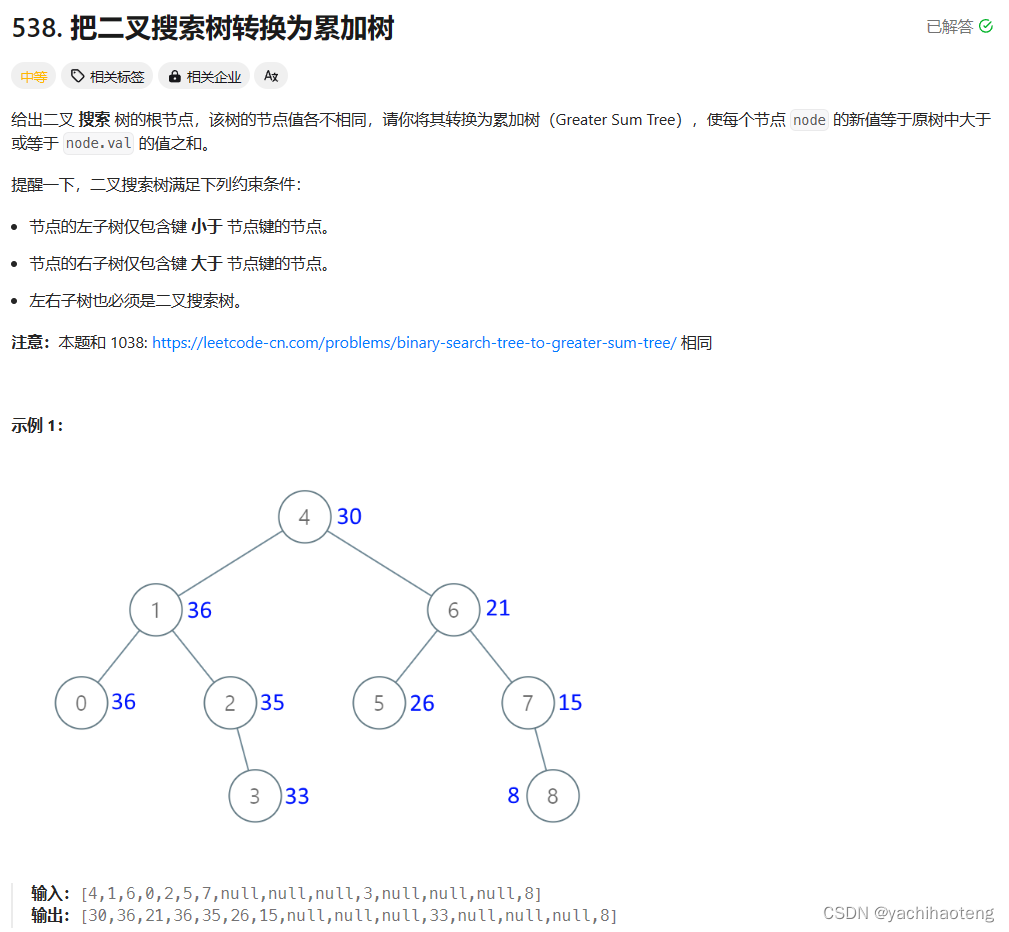
学习:本题最重要的是需要找到它的规律,本题是将每个节点的新值转变为等于原树中大于或等于node.val的值之和。如果将二叉搜索树通过中序遍历转化为数组来看的话,其实就是从后往前依次累加。因此本题应该采用的遍历方法是反中序遍历,通过右中左的遍历顺序,因此将节点值累加。
注意本题累加过程中,采用的是双指针的方法,需要一个指向当前节点的前一个节点pre来保存上一个节点的累加和。
代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:TreeNode* pre = nullptr; //指向当前节点的前一个节点//本题不需要返回值,只用将当前值改变就行void traversal(TreeNode* root) {//终止条件if(root == nullptr) return;//本题的遍历顺序应该为右中左//右traversal(root->right);//中if(pre != nullptr) {root->val = root->val + pre->val;}pre = root;//左traversal(root->left);}TreeNode* convertBST(TreeNode* root) {traversal(root);return root;}
};代码:本题也能够使用迭代法进行
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
private:int pre; // 记录前一个节点的数值void traversal(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) {st.push(cur);cur = cur->right; // 右} else {cur = st.top(); // 中st.pop();cur->val += pre;pre = cur->val;cur = cur->left; // 左}}}
public:TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};二叉树总结
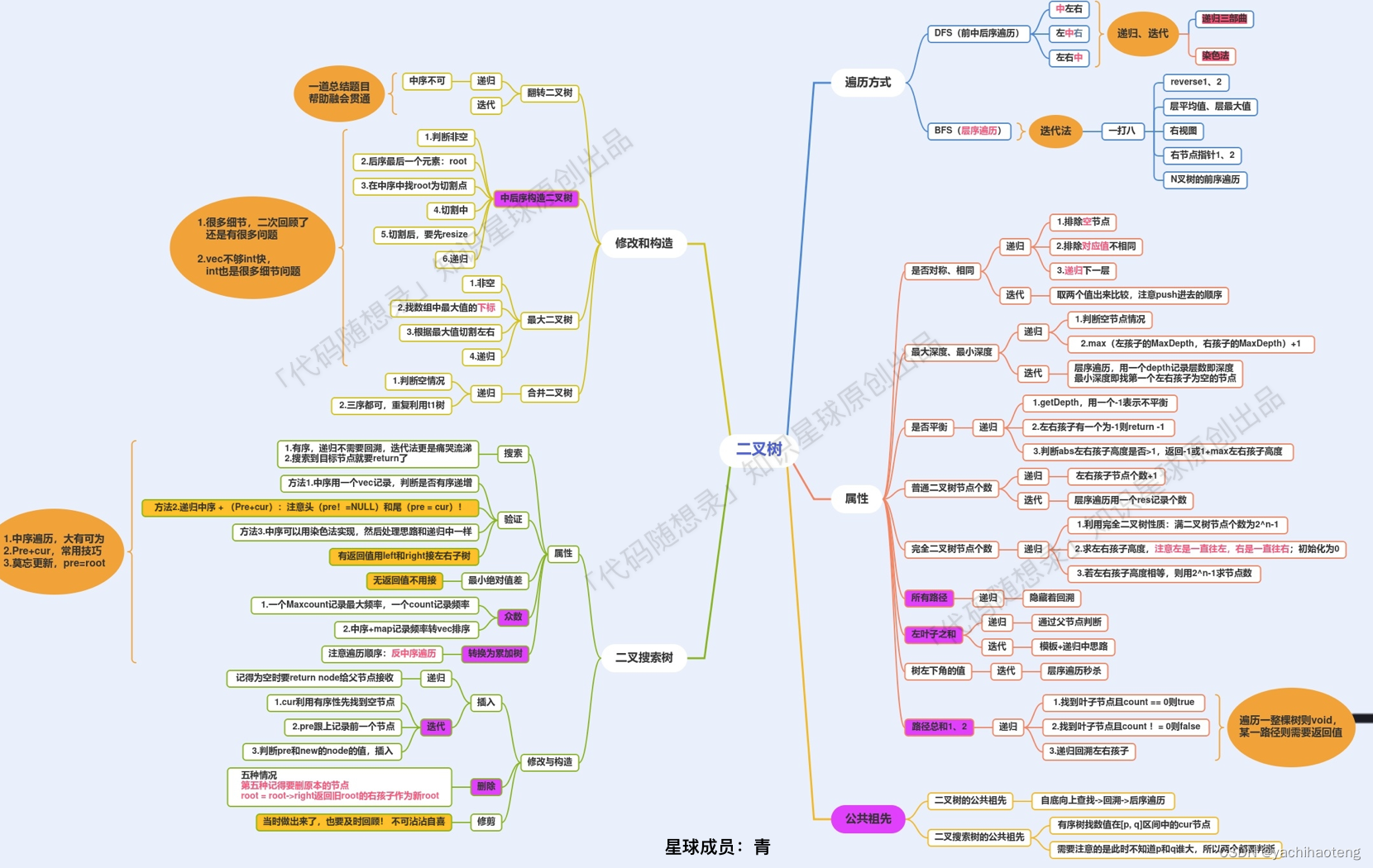
对于二叉树来说我们首先需要掌握的就是递归这一算法,确定递归三部曲掌握通过递归进行的二叉树的前序遍历、中序遍历、后序遍历的方法。
其次对于二叉树来说,它的迭代方法同样也很重要,递归由于其不断递归的特殊性,稍有不慎就容易导致栈溢出,且问题相对于迭代法不好排查。因此掌握迭代法对于实际工程使用也十分重要。
这七天我们对二叉树的遍历方式,各种属性,二叉树的修改和构造都进行了详细的练习。并且对二叉树中一个重要的类型二叉搜索树也进行了详细的考察,二叉搜索树自带的遍历顺序,能够便于解答很多问题,同时对二叉搜索树进行中序遍历能够得到一个非递减序列也是重要的性质之一。
总结来说:
-
涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定都是先构造中节点。
-
求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。(包括是否对称,求最大深度,最小深度,有多少个节点,是否平衡,路径问题,左叶子之和、左下角的值等)
-
求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
二叉树系列就这么完美结束了!
相关文章:

Studying-代码随想录训练营day21| 669.修建二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树、二叉树总结
第21天,二叉树最后一篇,冲💪 目录 669.修建二叉搜索树 108.将有序数组转换为二叉搜索树 538.把二叉搜索树转换为累加树 二叉树总结 669.修建二叉搜索树 文档讲解:代码随想录修建二叉搜索树 视频讲解:手撕修建二叉…...
GraphQL:简介
GraphQL 图片来源: 我们将探索GraphQL 的基础知识,并学习如何使用Apollo将其与 React 和 React Native 等前端框架连接起来。这将帮助您了解如何使用 GraphQL、React、React Native 和 Apollo 构建现代、高效的应用程序。 什么是 GraphQL?…...

AI大模型安全挑战和安全要求解读
引言 随着人工智能技术的飞速发展,大模型技术以其卓越的性能和广泛的应用前景,正在重塑人工智能领域的新格局。然而,任何技术都有两面性,大模型在带来前所未有便利的同时,也引发了深刻的安全和伦理挑战。 大模型&…...

前端面试题-token的存放位置
哈喽小伙伴们大家好,本系列是一个专门针对前端开发岗的面试题系列,每周将会不定期分享一些面试题,希望对大家有所帮助. 面试官:token 一般在客户端存在哪儿 求职者:Token一般在客户端存在以下几个地方: (1)Cookie:Token可以存储在客户端的Cookie中。服…...

深入探讨计算机网络中的各种报文
在计算机网络中,报文(Packet)是数据传输的基本单位。不同的协议使用不同类型的报文来实现数据传输的各种功能。本文将详细探讨计算机网络中常见的几种报文类型,并通过举例说明其具体应用。 一、TCP/IP协议栈中的报文 TCP/IP协议…...

Debezium系列之:Mysql和SQLServer数据库字段类型覆盖测试
Debezium系列之:Mysql和SQLServer数据库字段类型覆盖测试 一、需求背景二、类型对比三、完整流程三、Mysql数据库全字段类型覆盖测试四、SQLServer数据库字段类型覆盖测试一、需求背景 Debezium版本升级迭代,要做字段类型测试,确保版本间字段类型的差异下游能够自动适应,或…...
Mathtype7在Word2016中闪退(安装过6)
安装教程:https://blog.csdn.net/Little_pudding10/article/details/135465291 Mathtype7在Word2016中闪退是因为安装过Mathtype6,MathPage.wll和MathType Comm***.dotm),不会随着Mathtype的删除自动删除,而新版的Mathtype中的文件…...

SQL面试题练习 —— 合并用户浏览行为
目录 1 题目2 建表语句3 题解 1 题目 有一份用户访问记录表,记录用户id和访问时间,如果用户访问时间间隔小于60s则认为时一次浏览,请合并用户的浏览行为。 样例数据 ------------------------ | user_id | access_time | ---------------…...

【Docker】docker 替换宿主与容器的映射端口和文件路径
every blog every motto: You can do more than you think. https://blog.csdn.net/weixin_39190382?typeblog 0. 前言 docker 替换宿主与容器的映射端口和文件夹 1. 正文 1.1 关闭docker 服务 systemctl stop docker1.2 找到容器的配置文件 cd /var/lib/docker/contain…...

GPU算力租用平台推荐
推荐以下几家GPU算力租用平台: 1. AWS (Amazon Web Services) EC2 - AWS提供多种GPU实例,适合不同的计算需求,如机器学习、深度学习和图形渲染等。 - 优点:全球覆盖面广,稳定性高,服务支持全面。 …...
)
定个小目标之刷LeetCode热题(31)
238. 除自身以外数组的乘积 给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请 不要使用除法&#…...

我在高职教STM32——LCD液晶显示(3)
大家好,我是老耿,高职青椒一枚,一直从事单片机、嵌入式、物联网等课程的教学。对于高职的学生层次,同行应该都懂的,老师在课堂上教学几乎是没什么成就感的。正因如此,才有了借助 CSDN 平台寻求认同感和成就…...

uniapp横屏移动端卡片缩进轮播图
uniapp横屏移动端卡片缩进轮播图 效果: 代码: <!-- 简单封装轮播图组件:swiperCard --> <template><swiper class"swiper" circular :indicator-dots"true" :autoplay"true" :interval"10000&quo…...

整合Spring Boot和Apache Solr进行全文搜索
整合Spring Boot和Apache Solr进行全文搜索 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 在现代应用开发中,全文搜索是许多应用不可或缺的功能之…...

网络治理新模式:Web3时代的社会价值重构
随着Web3技术的崛起,传统的网络治理模式正在经历革新,这不仅仅是技术的进步,更是对社会价值观念的挑战和重构。本文将深入探讨Web3时代的网络治理新模式,其背后的技术基础、社会影响以及未来的发展方向。 1. 引言 Web3时代&#…...

[个人感悟] MySQL应该考察哪些问题?
前言 数据存储一直是软件开发中必不可少的一环, 从早期的文件存储txt, Excel, Doc, Access, 以及关系数据库时代的MySQL,SQL Server, Oracle, DB2, 乃至最近的大数据时代f非关系型数据库:Hadoop, HBase, MongoDB. 此外还有顺序型数据库InfluxDB, 图数据库Neo4J, 分布式数据库T…...
《数据结构与算法基础》学习笔记——1.2基本概念和术语
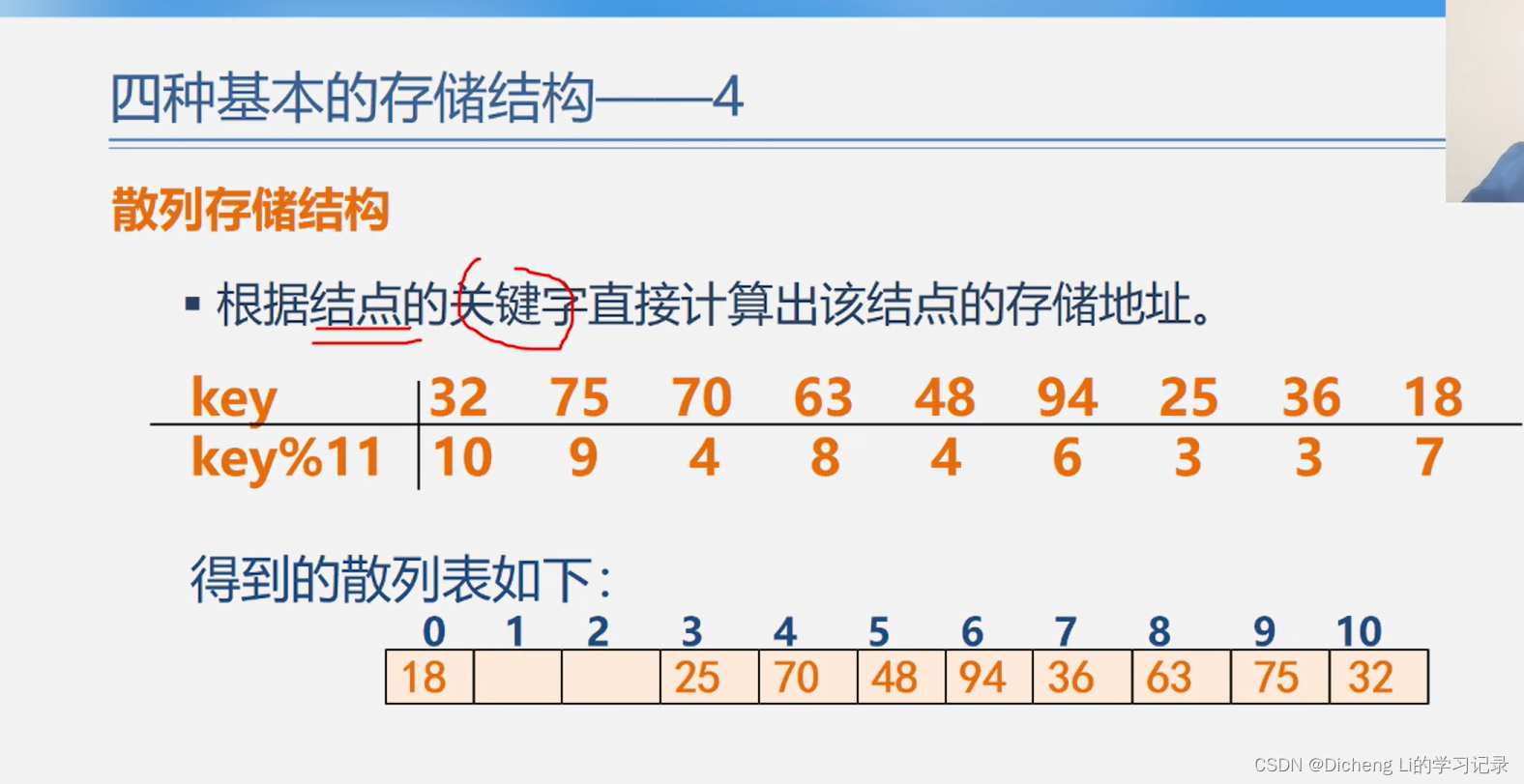
一、本章结构 二、四个数据相关专业名词的解释 两者的区别 三、数据结构相关内容 四、逻辑结构的分类 五、存储结构的分类及四种基本存储结构...
Java之线程相关应用实现
后台线程 一个进程中只有后台进程运行,该进程将会结束。 新创建的线程默认为前台线程,Java中只要有一个前台线程运行,就不会结束程序,如果只有后台线程运行,程序就会结束,可以在线程对象启动前执行setDae…...
一加全机型TWRP合集/橙狐recovery下载-20240603更新-支持一加12/Ace3V手机
TWRP是目前安卓平台的刷机神器,可快速刷写第三方ROM或官方系统,刷入TWRP之前需要解锁BL,目前已适配一加多个机型。ROM乐园小编20240603整理,涵盖一加1到一加Ace3V多机型专用TWRP文件,个人机型橙狐recovery适配相对完整…...

小伙子知道synchronized的优化过程吗
synchronized优化 背景:synchronized最初作为Java中的重量级锁,开销大,不被推荐使用。优化:随着JDK的发展,特别是JDK1.6以后,synchronized经历了优化,现在广泛应用于JVM源码和开源框架。 对象…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
