线性代数|机器学习-P18快速下降奇异值
文章目录
- 1. 为什么要低秩矩阵
- 1.1 矩阵A的秩定义
- 1.2 矩阵压缩PCA
- 2. 低秩矩阵图像处理
- 3. 秩的相关性质
- 3.1 秩的公差轴表示
- 3.2 Eckart-Young 定理
- 4. 低秩矩阵
- 4.1 低秩矩阵描述
- 4.2 函数低秩矩阵形式
- 4.3通项小结
- 4.4 函数采样拟合
- 5. 西尔维斯特方程
- 5.1 希尔伯特矩阵举例
- 5.2 范德蒙矩阵举例
- 5.3 西尔维斯特方程
1. 为什么要低秩矩阵
1.1 矩阵A的秩定义
如果矩阵X为n行n列实数矩阵,其有n个特征值如下:
σ 1 ≥ σ 2 ≥ ⋯ ≥ σ k ≥ σ k + 1 ≥ ⋯ ≥ σ n \begin{equation} \sigma_1\ge\sigma_2\ge\cdots\ge\sigma_k\ge\sigma_{k+1}\ge\cdots\ge\sigma_{n} \end{equation} σ1≥σ2≥⋯≥σk≥σk+1≥⋯≥σn
- 如果满足如下条件
σ k + 1 = 0 , σ k > 0 \begin{equation} \sigma_{k+1}=0,\sigma_k>0 \end{equation} σk+1=0,σk>0
那么可得:
r a n k ( X ) = k , X = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ k u k v k T \begin{equation} rank(X)=k,X=\sigma_1u_1v_1^T+\sigma_2u_2v_2^T+\cdots+\sigma_ku_kv_k^T \end{equation} rank(X)=k,X=σ1u1v1T+σ2u2v2T+⋯+σkukvkT
1.2 矩阵压缩PCA
我们的世界里面有很多数据,如果我们原封不动的发送数据,那么会导致数据量的增大,我们希望对数据进行压缩后再打包压缩,这样的话我们能够在带宽一定的情况下发送更多的数据,举例,假设我们有一个矩阵X,我们可以经过SVD奇异值分解得到如下:
-
假设矩阵 n × n n\times n n×n 矩阵的秩为k
X = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ k u k v k T + σ k + 1 u k + 1 v k + 1 T + ⋯ + σ n u n v n T \begin{equation} X=\sigma_1u_1v_1^T+\sigma_2u_2v_2^T+\cdots+\sigma_ku_kv_k^T+\sigma_{k+1}u_{k+1}v_{k+1}^T+\cdots+\sigma_nu_nv_n^T\end{equation} X=σ1u1v1T+σ2u2v2T+⋯+σkukvkT+σk+1uk+1vk+1T+⋯+σnunvnT -
我们知道矩阵X的奇异值关系如下:
σ 1 ≥ σ 2 ≥ ⋯ ≥ σ k ≥ σ k + 1 ≥ ⋯ ≥ σ n \begin{equation} \sigma_1\ge\sigma_2\ge\cdots\ge\sigma_k\ge\sigma_{k+1}\ge\cdots\ge\sigma_{n} \end{equation} σ1≥σ2≥⋯≥σk≥σk+1≥⋯≥σn -
如果矩阵X的秩为k,那么可得:
σ k + 1 = ⋯ = σ n = 0 \begin{equation} \sigma_{k+1}=\cdots=\sigma_{n}=0 \end{equation} σk+1=⋯=σn=0 -
在没有低秩压缩的情况下,我们发送数据大小 S 1 S_1 S1为,直接长=n宽=n相乘
S 1 = n ∗ n = n 2 \begin{equation} S_1=n*n=n^2 \end{equation} S1=n∗n=n2 -
SVD奇异值分解后可得:
X = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ k u k v k T \begin{equation} X=\sigma_1u_1v_1^T+\sigma_2u_2v_2^T+\cdots+\sigma_ku_kv_k^T \end{equation} X=σ1u1v1T+σ2u2v2T+⋯+σkukvkT -
在低秩压缩的后下,我们发送数据大小 S 2 S_2 S2为,其中每个
S 2 = ( n + n ) ∗ k = 2 n k \begin{equation} S_2=(n+n)*k=2nk \end{equation} S2=(n+n)∗k=2nk

-
那么我们可以得到如下:
2 n k ≤ n 2 → k ≤ n 2 \begin{equation} 2nk\leq n^2\rightarrow k\leq\frac{n}{2} \end{equation} 2nk≤n2→k≤2n -
那问题来了,我们能够做得更好吗?我们能够用更小的数据来压缩吗?
2. 低秩矩阵图像处理
假设我们有一张日本国旗的图像表示如下,我们

- 如图所示,我们可以依据对称性,将一个日本国旗拆解为如下三个部分,每个部分的秩表示如下,注意要取整:
r 1 = ( 1 − 2 2 ) r ; r 2 = ( 1 − 2 2 ) r ; r 3 = 1 \begin{equation} r_1=(1-\frac{\sqrt{2}}{2})r;r_2=(1-\frac{\sqrt{2}}{2})r;r_3=1 \end{equation} r1=(1−22)r;r2=(1−22)r;r3=1 - 那么拆解后,数据的秩表示如下:
r k = ( 2 − 2 ) r + 1 \begin{equation} r_k=(2-\sqrt{2})r+1 \end{equation} rk=(2−2)r+1 - 小结:对于一个原始的日本国旗图像来说,我们通过对称的原理,不断的对称分解得到三个最小的无法对称的三个小图像,这样我们可以将原来的日本国旗图像最后分解为三个小图像发给对方,当对方收到三个小图像后,可以通过对称原理进行还原,这样数据就压缩了,我们可以进行数据低秩压缩处理。
- 整体思路如下:

3. 秩的相关性质
3.1 秩的公差轴表示
假设我们有一个公差 0 < ϵ < 1 0<\epsilon<1 0<ϵ<1, 如果满足 σ k + 1 ≤ ϵ σ 1 ( x ) , σ k ≥ ϵ σ 1 ( x ) \sigma_{k+1}\le \epsilon\sigma_1(x),\sigma_{k}\ge \epsilon\sigma_1(x) σk+1≤ϵσ1(x),σk≥ϵσ1(x),则 r a n k ϵ = k rank_{\epsilon}=k rankϵ=k
- 我们知道 0 < ϵ < 1 0<\epsilon<1 0<ϵ<1,两百年乘以 σ 1 ( x ) \sigma_1(x) σ1(x) 可得:
0 < ϵ σ 1 ( x ) < σ 1 ( x ) \begin{equation} 0<\epsilon\sigma_1(x)<\sigma_1(x) \end{equation} 0<ϵσ1(x)<σ1(x) - 也就是说 ϵ σ 1 ( x ) \epsilon\sigma_1(x) ϵσ1(x) 可以取到所有大于零的奇异值

- 也就是说我们能够在 σ k ( x ) \sigma_k(x) σk(x)这个点上面找到奇异值的正负边界,那么我们就能够知道秩为k。
3.2 Eckart-Young 定理
假设矩阵B有和矩阵 A k A_k Ak一样的值为k,那么可得如下结论:

∣ ∣ A − B ∣ ∣ ≥ ∣ ∣ A − A k ∣ ∣ \begin{equation} ||A-B|| \geq ||A-A_k|| \end{equation} ∣∣A−B∣∣≥∣∣A−Ak∣∣
- 画图证明:
假设我们定义矩阵A为一个向量, A k A_k Ak为矩阵A向量的子向量,定义矩阵B的秩为k,那么矩阵B向量的长度和向量 A k A_k Ak长度一样,方向不同,具体如下图所述:

-由于 0 ° < θ < 90 ° 0°<\theta<90° 0°<θ<90°,所以可得 90 ° < β < 180 ° 90°<\beta<180° 90°<β<180°,也就是说在新的三角形中, β \beta β是钝角,那么钝角对应的边最大,所以可得 ∣ ∣ C ∣ ∣ ≥ ∣ ∣ D ∣ ∣ ||C||\ge ||D|| ∣∣C∣∣≥∣∣D∣∣,可以得到结论如下:
∣ ∣ A − B ∣ ∣ ≥ ∣ ∣ A − A k ∣ ∣ \begin{equation} ||A-B||\geq ||A-A_k|| \end{equation} ∣∣A−B∣∣≥∣∣A−Ak∣∣ - 那么 σ k + 1 = ∣ ∣ A − A k ∣ ∣ \sigma_{k+1}=||A-A_k|| σk+1=∣∣A−Ak∣∣暂时不会,后面补充吧!!
4. 低秩矩阵
4.1 低秩矩阵描述
-
4.1 hilbert 希尔伯特矩阵
我们定义希尔伯特矩阵如下:
H j k = 1 j + k − 1 \begin{equation} H_{jk}=\frac{1}{j+k-1} \end{equation} Hjk=j+k−11 -
4.2 Vandermonde 范德蒙矩阵
我们定义范德蒙矩阵如下:
V n = [ 1 x 1 x 1 2 ⋯ x 1 n − 1 1 x 2 x 2 2 ⋯ x 2 n − 1 ⋮ ⋮ ⋮ ⋯ ⋮ 1 x n x n 2 ⋯ x n n − 1 ] \begin{equation} V_{n}=\begin{bmatrix} 1&x_1&x_1^2&\cdots&x_1^{n-1}\\\\ 1&x_2&x_2^2&\cdots&x_2^{n-1}\\\\ \vdots&\vdots&\vdots&\cdots&\vdots\\\\ 1&x_n&x_n^2&\cdots&x_n^{n-1} \end{bmatrix} \end{equation} Vn= 11⋮1x1x2⋮xnx12x22⋮xn2⋯⋯⋯⋯x1n−1x2n−1⋮xnn−1 -
其中 A n = [ a i j ] A_n=[a_{ij}] An=[aij]时一个 n × n n\times n n×n阶矩阵,每个元素为 a i j = x i j − 1 a_{ij}=x_i^{j-1} aij=xij−1
经常我们需要求解 V n − 1 V_{n}^{-1} Vn−1,但是因为 V n V_n Vn是低秩矩阵,所以很难求解其逆矩阵,那为什么这么难求这些低秩矩阵的逆呢?原因居然是世界是平滑的,所以存在很多低秩的矩阵。
4.2 函数低秩矩阵形式
假设我们有一个函数表示如下:
P ( x , y ) = 1 + x + x y → X j k = P ( j , k ) \begin{equation} P(x,y)=1+x+xy\rightarrow X_{jk}=P(j,k) \end{equation} P(x,y)=1+x+xy→Xjk=P(j,k)
- 那么矩阵X可以表示如下:
X = [ 1 1 ⋮ 1 ] [ 1 1 ⋯ 1 ] + [ 1 2 ⋮ n ] [ 1 1 ⋯ 1 ] + [ 1 2 ⋮ n ] [ 1 2 ⋯ n ] \begin{equation} X=\begin{bmatrix} 1\\\\1\\\\\vdots\\\\1 \end{bmatrix}\begin{bmatrix} 1&1&\cdots&1 \end{bmatrix}+\begin{bmatrix} 1\\\\2\\\\\vdots\\\\n \end{bmatrix}\begin{bmatrix} 1&1&\cdots&1 \end{bmatrix}+\begin{bmatrix} 1\\\\2\\\\\vdots\\\\n \end{bmatrix}\begin{bmatrix} 1&2&\cdots&n \end{bmatrix} \end{equation} X= 11⋮1 [11⋯1]+ 12⋮n [11⋯1]+ 12⋮n [12⋯n] - 那么可以得到矩阵X的秩小于3,即 R a n k ( X ) ≤ 3 Rank(X)\le3 Rank(X)≤3
4.3通项小结
假设我们有如下函数
p ( x , y ) = ∑ s = 0 m − 1 ∑ t = 0 m − 1 a s t x s y t , X j k = p ( j , k ) \begin{equation} p(x,y)=\sum_{s=0}^{m-1}\sum_{t=0}^{m-1}a_{st}x^sy^t,X_{jk}=p(j,k) \end{equation} p(x,y)=s=0∑m−1t=0∑m−1astxsyt,Xjk=p(j,k)
- 那么我们可以得到矩阵X的秩有如下关系:
r a n k ( X ) ≤ m 2 \begin{equation} rank(X)\leq m^2 \end{equation} rank(X)≤m2
4.4 函数采样拟合
假设我们有一个矩阵X且 X j k = 1 j + k − 1 , f ( x , y ) = 1 x + y − 1 X_{jk}=\frac{1}{j+k-1},f(x,y)=\frac{1}{x+y-1} Xjk=j+k−11,f(x,y)=x+y−11,我们希望通过在 f ( x , y ) f(x,y) f(x,y)函数中采样的方法得到一个近似的函数 p ( x , y ) p(x,y) p(x,y),使得我们能够在进行了有限的采样后,我们只需要用 p ( x , y ) p(x,y) p(x,y)近似于原函数 f ( x , y ) f(x,y) f(x,y)
∣ f ( x , y ) − p ( x , y ) ∣ ≤ ϵ n ∣ ∣ x ∣ ∣ 2 \begin{equation} |f(x,y)-p(x,y)|\leq \frac{\epsilon}{n}||x||_2 \end{equation} ∣f(x,y)−p(x,y)∣≤nϵ∣∣x∣∣2
- 是不是很神奇,用有限的采样可以拟合出来原来的函数。
假设我们有一个希尔伯特矩阵,其秩为1000,假设我们有一个公差 ϵ = 1 0 − 15 \epsilon=10^{-15} ϵ=10−15,Reade's大神得到秩为
r a n k ϵ ( H 1000 ) ≤ 719 \begin{equation} rank_{\epsilon}(H_{1000})\leq 719 \end{equation} rankϵ(H1000)≤719
5. 西尔维斯特方程
Sylvester 方程:
A X + X B = C \begin{equation} AX+XB=C \end{equation} AX+XB=C
其中A、B及C是已知的矩阵,问题是要找出符合条件的X。其中所有矩阵的系数都是复数。为了要使方程成立,矩阵的行和列需要满足一定条件,A和B都要是方阵,大小分别是n和m,而X和C要是n行m列的矩阵,n和m也可以相等,四个矩阵都是大小相同的方阵。
西尔维斯特方程有唯一解X的充分必要条件是A和-B没有共同的特征值。
AX+XB=C也可以视为是(可能无穷维中)巴拿赫空间中有界算子的方程。此情形下,唯一解X的充份必要条件几乎相同:唯一解X的充份必要条件是A和-B的谱互为不交集
5.1 希尔伯特矩阵举例
[ 1 2 3 2 ⋱ n − 1 2 ] H − H [ − 1 2 − 3 2 ⋱ − n + 1 2 ] = [ 1 1 ⋯ 1 1 1 ⋯ 1 ⋮ ⋮ ⋯ ⋮ 1 1 ⋯ 1 ] \begin{equation} \begin{bmatrix} \frac{1}{2}\\\\ &\frac{3}{2}\\\\ &&\ddots\\\\ &&&n-\frac{1}{2} \end{bmatrix}H-H\begin{bmatrix} -\frac{1}{2}\\\\ &-\frac{3}{2}\\\\ &&\ddots\\\\ &&&-n+\frac{1}{2} \end{bmatrix}=\begin{bmatrix} 1&1&\cdots&1\\\\ 1&1&\cdots&1\\\\ \vdots&\vdots&\cdots&\vdots\\\\ 1&1&\cdots&1 \end{bmatrix} \end{equation} 2123⋱n−21 H−H −21−23⋱−n+21 = 11⋮111⋮1⋯⋯⋯⋯11⋮1
- 我们那H中的第i,j项目来说;
H i j = 1 i + j − 1 \begin{equation} H_{ij}=\frac{1}{i+j-1} \end{equation} Hij=i+j−11
( i − 1 2 ) ⋅ 1 i + j − 1 − ( − j + 1 2 ) 1 i + j − 1 = i + j − 1 i + j − 1 = 1 \begin{equation} (i-\frac{1}{2})\cdot\frac{1}{i+j-1}-(-j+\frac{1}{2})\frac{1}{i+j-1}=\frac{i+j-1}{i+j-1}=1 \end{equation} (i−21)⋅i+j−11−(−j+21)i+j−11=i+j−1i+j−1=1 - 既然每个元素结果为1,所以最后结果为全1矩阵。
5.2 范德蒙矩阵举例
A = [ x 1 x 2 ⋱ x n ] ; B = [ 0 0 ⋯ − 1 1 0 0 ⋯ ⋅ 0 1 0 ⋱ 0 0 0 1 0 ] ; C = [ 0 0 0 x 1 n + 1 0 0 0 x 2 n + 1 0 0 0 ⋮ 0 0 0 x n n + 1 ] ; \begin{equation} A=\begin{bmatrix}x_1\\\\ &x_2\\\\ &&\ddots\\\\ &&&x_n\end{bmatrix}; B=\begin{bmatrix} 0&0&&\cdots&-1\\\\ 1&0&0&\cdots&\cdot\\\\ 0&1&0&\ddots&0\\\\ 0&0&1&&0\end{bmatrix}; C=\begin{bmatrix} 0&0&0&x_1^n+1\\\\ 0&0&0&x_2^n+1\\\\ 0&0&0&\vdots\\\\ 0&0&0&x_n^n+1 \end{bmatrix}; \end{equation} A= x1x2⋱xn ;B= 01000010001⋯⋯⋱−1⋅00 ;C= 000000000000x1n+1x2n+1⋮xnn+1 ;
5.3 西尔维斯特方程
如果 X满足如下方程:
A X − X B = C \begin{equation} AX-XB=C \end{equation} AX−XB=C
- A,B是正规矩阵,E为A的特征值集合,F为B的的特征值集合,那么可以得到如下:
σ r k + 1 ( X ) ≤ Z k [ σ ( A ) , σ ( B ) ] σ 1 ( X ) → r a n k ( C ) = r ; \begin{equation} \sigma_{rk+1}(X)\le Z_{k}[\sigma(A),\sigma(B)]\sigma_1(X)\rightarrow rank(C)=r; \end{equation} σrk+1(X)≤Zk[σ(A),σ(B)]σ1(X)→rank(C)=r;
相关文章:

线性代数|机器学习-P18快速下降奇异值
文章目录 1. 为什么要低秩矩阵1.1 矩阵A的秩定义1.2 矩阵压缩PCA 2. 低秩矩阵图像处理3. 秩的相关性质3.1 秩的公差轴表示3.2 Eckart-Young 定理 4. 低秩矩阵4.1 低秩矩阵描述4.2 函数低秩矩阵形式4.3通项小结4.4 函数采样拟合 5. 西尔维斯特方程5.1 希尔伯特矩阵举例5.2 范德蒙…...
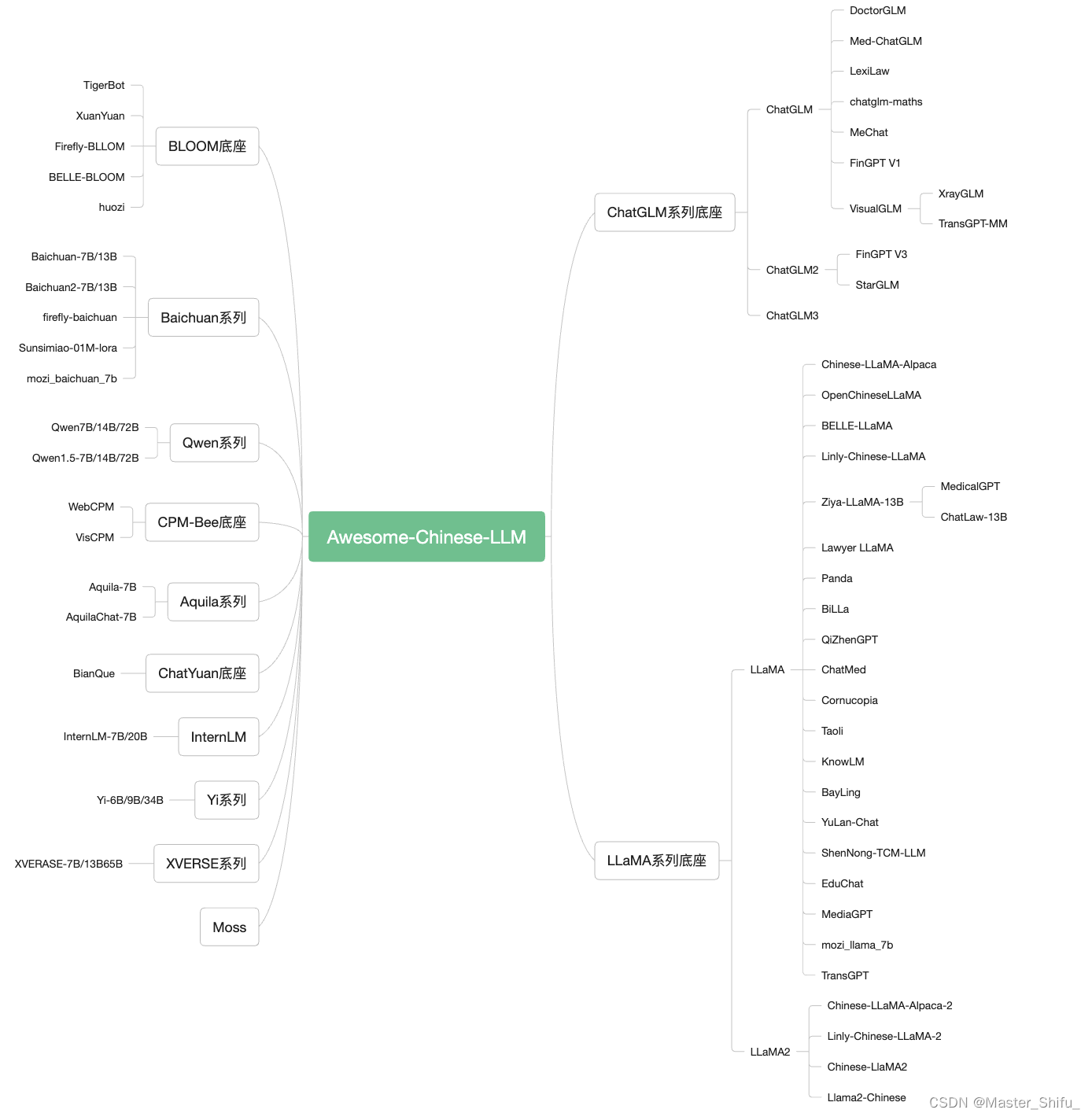
本地离线模型搭建指南-中文大语言模型底座选择依据
搭建一个本地中文大语言模型(LLM)涉及多个关键步骤,从选择模型底座,到运行机器和框架,再到具体的架构实现和训练方式。以下是一个详细的指南,帮助你从零开始构建和运行一个中文大语言模型。 本地离线模型搭…...

【代码随想录】【算法训练营】【第51天】 [115]不同的子序列 [583]两个字符串的删除操作 [72]编辑距离
前言 思路及算法思维,指路 代码随想录。 题目来自 LeetCode。 day 51,周四,又是不能坚持的一天~ 题目详情 [115] 不同的子序列 题目描述 115 不同的子序列 解题思路 前提: 思路: 重点: 代码实现 …...

24下半年软考集合!30s打破信息差!
01软考是什么? 软考,全称为计算机技术与软件专业技术资格(水平)考试,也称为计算机资格考试,是由国家人力资源和社会保障部、工业和信息化部领导的国家级考试。它既是国家级资格证书,又是职称资…...

如何在Xcode中设置库路径
在Xcode中设置库路径的过程可以分为以下几个步骤,下面将结合参考文章中的信息,以清晰、分点表示和归纳的方式给出指导: 1. 确定库的类型和来源 动态库(.dylib或.framework)或静态库(.a)&#…...
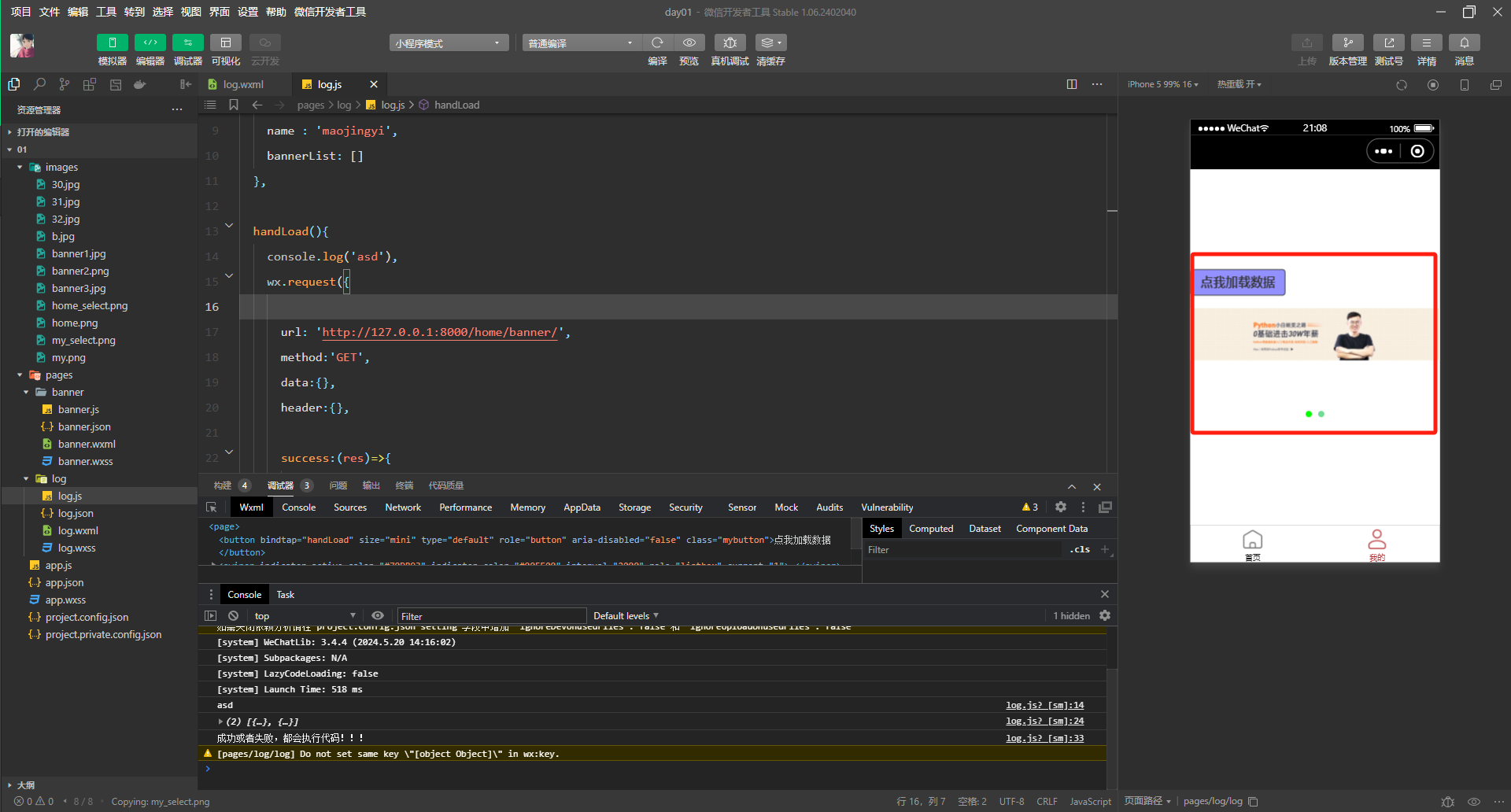
小程序的基本使用
【 0 】前言 【 0 】 这个就是js代码的存放地方 app.json // pages/banner/banner.js Page({/*** 页面的初始数据*/data: {},/*** 生命周期函数--监听页面加载*/onLoad(options) {},/*** 生命周期函数--监听页面初次渲染完成*/onReady() {},/*** 生命周期函数--监听页面显示…...
[保姆级教程]uniapp设置字体引入字体格式
文章目录 在 UniApp 中设置和引入自定义字体(如 .ttf、.woff、.woff2 等格式)通常涉及几个步骤。 准备字体文件: 首先,你需要有字体文件。这些文件通常以 .ttf、.woff 或 .woff2 格式提供。确保有权使用这些字体,并遵守…...
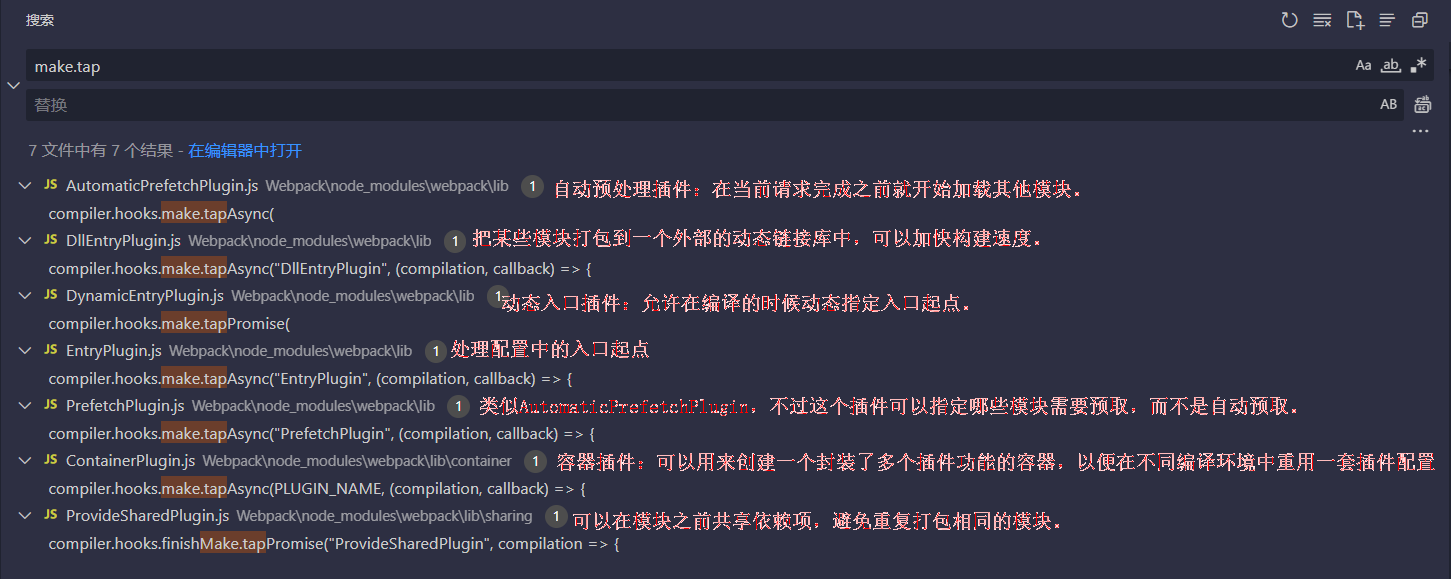
【Webpack】前端工程化之Webpack与模块化开发
目 录 前言模块化开发Stage1 - 文件划分方式Stage2 - 命名空间方式Stage3 - IIFE(立即调用函数表达式)Stage 4 - IIFE 依赖参数模块化的标准规范 使用Webpack实现模块化打包安装WebpackWebpack基本配置Webpack构建流程Webpack热更新Webpack打包优化 前言…...
【Android】记录在自己的AMD处理器无法使用Android studio 虚拟机处理过程
文章目录 问题:无法在AMD平台打开Android studio 虚拟机,已解决平台:AMD 5700g系统:win10专业版1、在 amd平台上使用安卓虚拟机需要安装硬件加速器2、关闭win10上的系统服务 问题:无法在AMD平台打开Android studio 虚拟…...
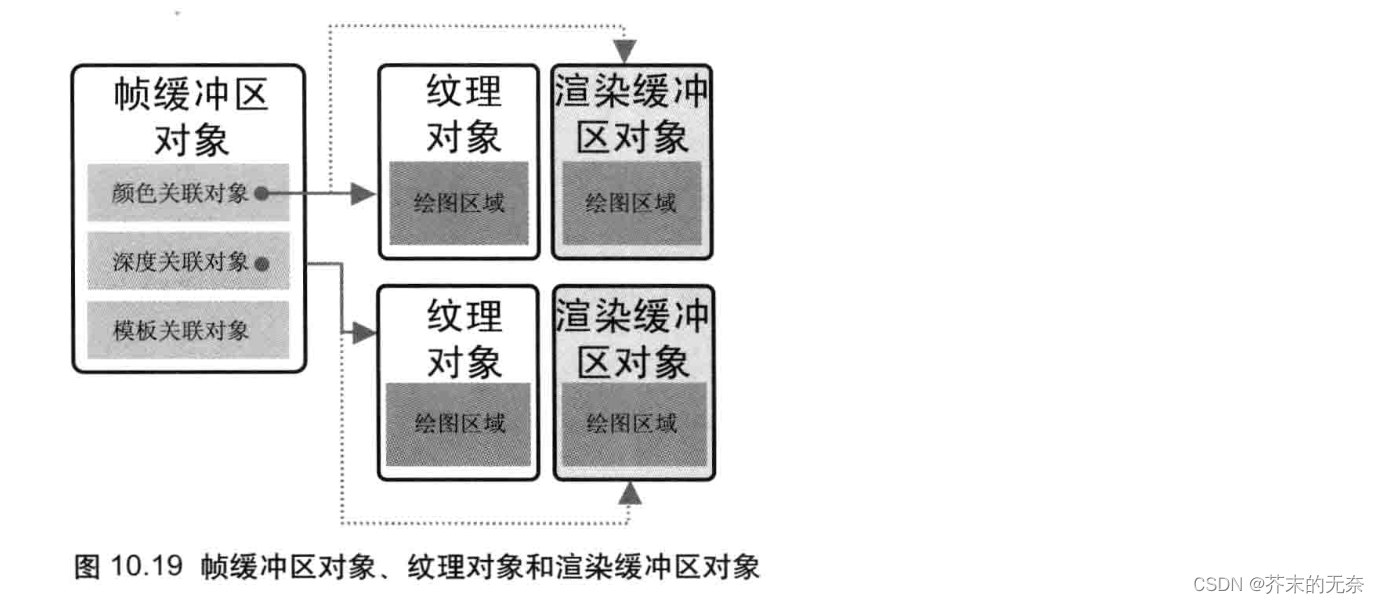
LearnOpenGL - Android OpenGL ES 3.0 使用 FBO 进行离屏渲染
系列文章目录 LearnOpenGL 笔记 - 入门 01 OpenGLLearnOpenGL 笔记 - 入门 02 创建窗口LearnOpenGL 笔记 - 入门 03 你好,窗口LearnOpenGL 笔记 - 入门 04 你好,三角形OpenGL - 如何理解 VAO 与 VBO 之间的关系LearnOpenGL - Android OpenGL ES 3.0 绘制…...
人工智能虚拟仿真系统,解决算法难、编程难、应用场景难三大难题
近年来,人工智能技术迅猛发展,广泛渗透至各行业,市场份额持续扩大,预示着智能化转型的广阔前景。该行业本质上属于知识高度密集型,近年来的迅猛发展进一步加剧了对专业人才的迫切需求。 然而,我国目前在人工…...
和视图在查询时的性能影响)
CTE(公共表表达式)和视图在查询时的性能影响
在SQL查询优化和数据库设计中,CTE(公共表表达式)和视图都是常用的工具。尽管它们在功能和使用场景上有很多相似之处,但在查询性能方面可能存在显著差异。本文将探讨CTE和视图在查询时的性能影响,帮助您在实际项目中做出…...
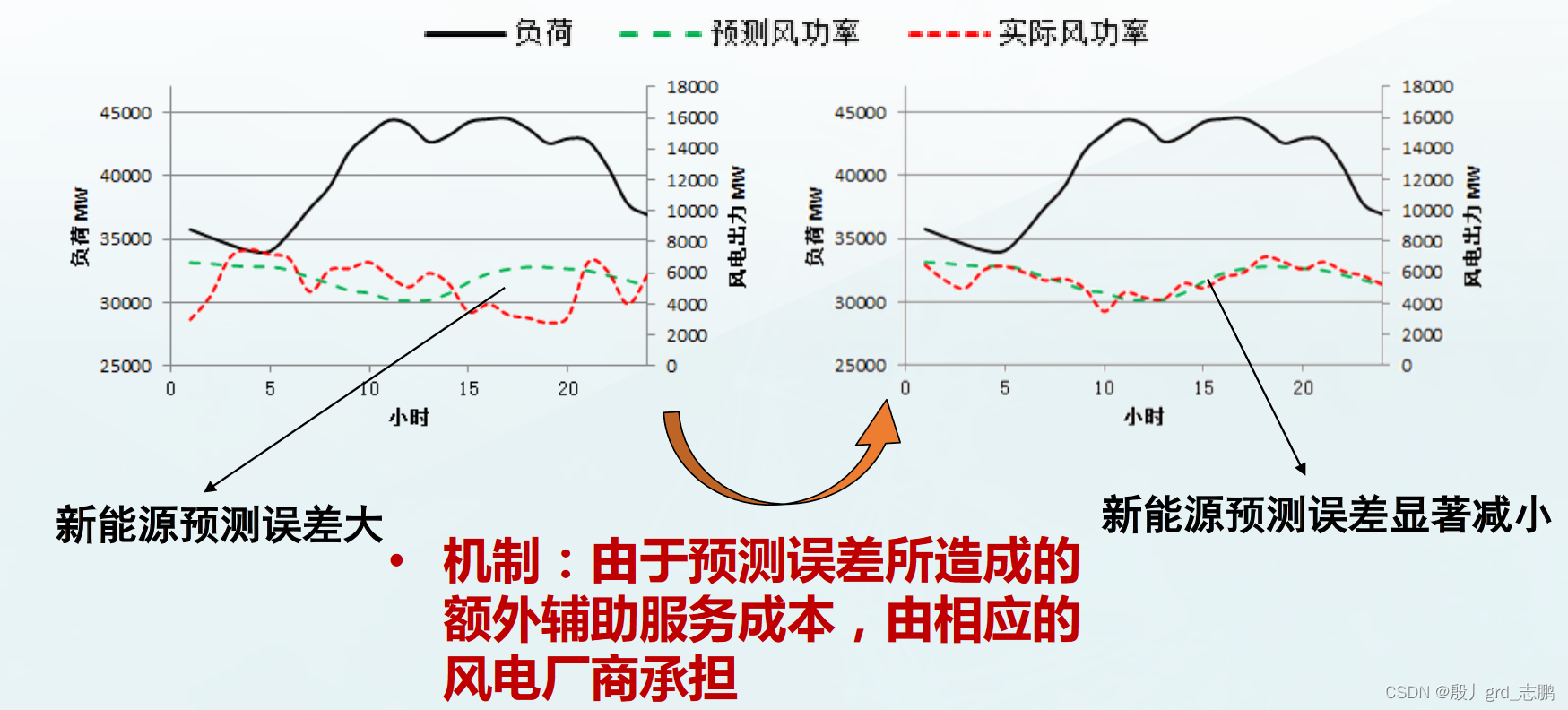
新能源行业必会基础知识-----电力市场概论笔记-----绪论
新能源行业知识体系-------主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/139946830 目录 1. 电力市场的定义2. 对传统电力系统理论的挑战 1. 电力市场的定义 1. 我国电力市场的进程 我国新一轮电力体制改革的5大亮点&…...
003 SpringBoot操作ElasticSearch7.x
文章目录 5.SpringBoot集成ElasticSearch7.x1.添加依赖2.yml配置3.创建文档对象4.继承ElasticsearchRepository5.注入ElasticsearchRestTemplate 6.SpringBoot操作ElasticSearch1.ElasticsearchRestTemplate索引操作2.ElasticsearchRepository文档操作3.ElasticsearchRestTempl…...

npm install报错Maximum call stack size exceeded
npm 报错 方案: npm cache clean --force npm install...
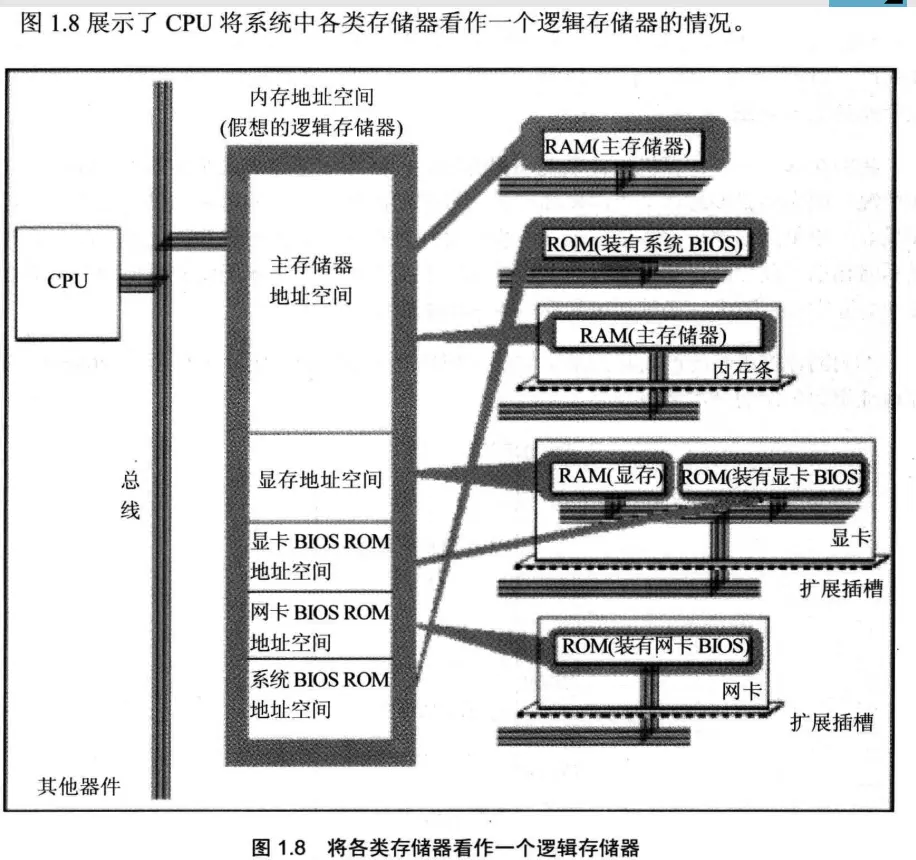
第1章 基础知识
第1章 基础知识 1.1 机器语言 机器语言就是机器指令的集合,机器指令展开来讲就是一台机器可以正确执行的命令 1.2 汇编语言的产生 汇编语言的主题是汇编指令。汇编指令和机器指令的差别在于指令的表示方法上,汇编指令是机器指令便于记忆的书写格式。…...

python脚本 限制 外部访问 linux服务器端口
注意:该脚本会清空linux防火墙的filter表的规则和用户自定义链路 脚本的效果是将端口限制为仅服务器内部访问 可以提供ip地址白名单 具体脚本: #!/usr/bin/python3 import argparse, subprocess, sys, redef popen(cmd):global resulttry:result su…...
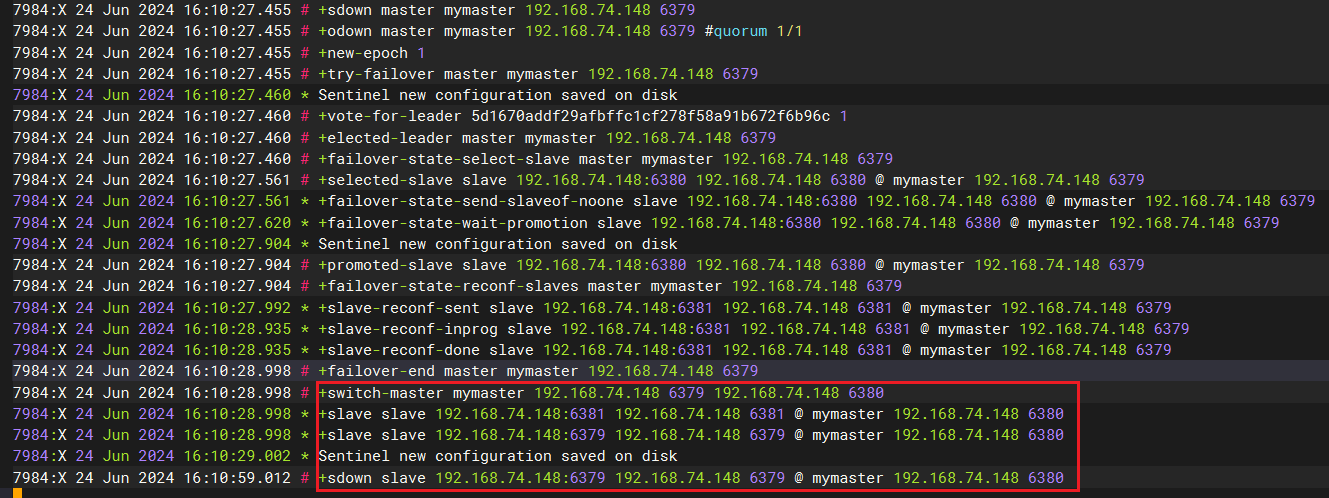
Redis-哨兵模式-主机宕机-推选新主机的过程
文章目录 1、为哨兵模式准备配置文件2、启动哨兵3、主机6379宕机3.4、查看sentinel控制台日志3.5、查看6380主从信息 4、复活63794.1、再次查看sentinel控制台日志 1、为哨兵模式准备配置文件 [rootlocalhost redis]# ll 总用量 244 drwxr-xr-x. 2 root root 150 12月 6 2…...
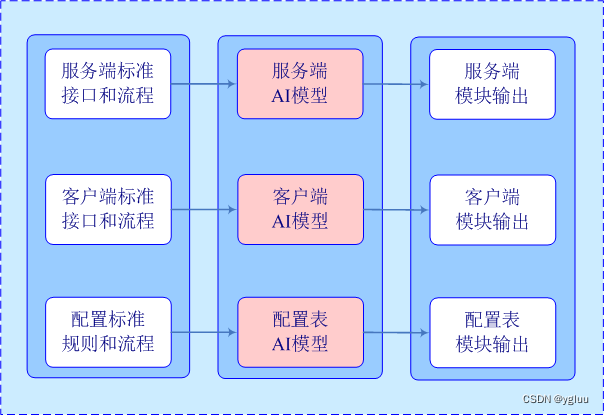
游戏工厂:AI(AIGC/ChatGPT)与流程式游戏开发
游戏工厂:AI(AIGC/ChatGPT)与流程式游戏开发 码客 卢益贵 ygluu 关键词:AI(AIGC、ChatGPT、文心一言)、流程式管理、好莱坞电影流程、电影工厂、游戏工厂、游戏开发流程、游戏架构、模块化开发 一、前言…...

每日一练 - OSPF 组播地址
01 真题题目 判断以下陈述是否正确: 224.0.0.6 是 ALL DRouters 监听地址 224.0.0.5 是 ALL SPFRouters 监听地址 A.正确 B.错误 02 真题答案 A 03 答案解析 在OSPF (Open Shortest Path First) 路由协议中,为了实现高效的信息交换和发现邻居&#x…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
