工厂模式与抽象工厂
原理:逻辑和业务全部封装 不需要细节 只要结果
示例:
# 简单工厂
class SimpleFactory:# 产品@staticmethoddef product(name):return nameif __name__ == "__main__":product = SimpleFactory.product("Gitee")print(product)- 装饰器@staticmethod,普通方法,类对象实例对象都可应用
- 装饰的方法类比产品,工厂生产产品,只要最后结果
抽象工厂实例:
from abc import ABCMeta, abstractmethod # 抽象工厂class TestMeta(metaclass=ABCMeta): 继承metaclass=ABCMetadef __init__(self):self.a = 1@abstractmethoddef fun(self):passclass TestOne(TestMeta):def __init__(self):super().__init__() # 调用父类的init# TestMeta.__init__()self.b = 1# 重写抽象方法def fun(self):print("拼接三方登录的url")- 抽象工厂类似于生活中的橘子,橘子的种类繁多,但橘子本体的一些口感(方法)是其他种类必须所拥有的,也就是其他类继承抽象工厂类,必须重写已有的方法,否则报错
- pass是占位符,抽象工厂中的方法要用装饰器@abstractmethod定义,只定义框架,不写具体逻辑
抽象工厂完成第三方登录基本方法:
class LoginProvide(metaclass=ABCMeta):# 跳转拼接@abstractmethoddef get_url(self):pass# 获取token@abstractmethodasync def get_token(self, code):pass# 获取用户信息@abstractmethodasync def get_info(self, token):pass# 用户信息存储@abstractmethodasync def set_user(self, user):passgitee登录实例
class GiteeProvider(LoginProvide):def __repr__(self):return "Gitee登录"def get_url(self):url = SITE_TYPE["Gitee"]["url"] # 跳到授权地址return urlasync def get_token(self, code):# 通过授权码请求token# 异步发送网络请求,防止阻塞client_id = SITE_TYPE["Gitee"]["client_id"]client_secret = SITE_TYPE["Gitee"]["client_secret"]redirect_uri = SITE_TYPE["Gitee"]["redirect_uri"]async with httpx.AsyncClient() as client:res = await client.post(url=f"https://gitee.com/oauth/token?grant_type=authorization_code&code={code}&client_id={client_id}&redirect_uri={redirect_uri}&client_secret={client_secret}",timeout=20)res = res.json()# 获取gitee的access_token refresh_tokenreturn res["access_token"]async def get_info(self, token):async with httpx.AsyncClient() as client:res = await client.get(SITE_TYPE["Gitee"]["gitee_get_info_uri"] + token, timeout=20)res = res.json()user = {"gitee_id": res["id"],"gitee_username": res["name"]}return userasync def set_user(self, user):gitee_id = user["gitee_id"]gitee_username = user["gitee_username"]username = (str(gitee_id) + "_" + str(gitee_username))try:# 曾经使用过gitee账号await db.get(UserModel.select().where((UserModel.username == username)& (UserModel.site_type == SITE_TYPE["Gitee"]["num"])))except Exception as e:print(e.args)await db.create(UserModel,username=username,site_type=SITE_TYPE["Gitee"]["num"])finally:mj = MyJwt()# 生成带有生命周期的tokentoken = mj.encode_date({"username": username,"site_type": SITE_TYPE["Gitee"]["num"]})# 生成refresh_token redis里面存refresh_token = await mj.set_refresh_token(f"{gitee_id}_{gitee_username}")# 中间缓存页url = SITE_TYPE["Gitee"]["gitee_center_uri"] + f"?gitee_refresh_token={refresh_token}&gitee_token={token}&username={username}"return urlGitee简化版:
# gitee登录简化版
class GiteeFactory(BaseHandler):def __init__(self, *args, **kwargs):super().__init__(*args, **kwargs)self.gitee = GiteeProvider()async def get(self):code = self.get_argument("code")access_token = await self.gitee.get_token(code)user = await self.gitee.get_info(access_token)url = await self.gitee.set_user(user)return self.redirect(url)# 路由
urlpatterns = [(r"/gitee_back/", GiteeFactory), # gitee
]总结:
- 利用抽象工厂模式,来编写架子,方便区分步骤,简洁明了
- 继承抽象工厂必须要重写所有方法
- 养成良好的代码习惯,方便给客户调用,保护内部细节
相关文章:

工厂模式与抽象工厂
原理:逻辑和业务全部封装 不需要细节 只要结果 示例: # 简单工厂 class SimpleFactory:# 产品staticmethoddef product(name):return nameif __name__ "__main__":product SimpleFactory.product("Gitee")print(product) 装饰器…...

什么?你不知道 ConcurrentHashMap 的 kv 不能为 null?
一、背景 最近设计某个类库时使用了 ConcurrentHashMap 最后遇到了 value 为 null 时报了空指针异常的坑。 本文想探讨下以下几个问题: (1) Map接口的常见子类的 kv 对 null 的支持情况。 (2)为什么 ConcurrentHashM…...

SQL复习04 | 复杂查询
1. 视图 视图和表的区别: 表保存的是实际的数据视图保存的是SELECT语句 视图的优点: 视图无需保存数据,可节省存储设备的容量可以将频繁使用的SELECT语句保存成视图,可大大提高效率 1.1 创建视图 CREATE VIEW 视图名称&…...
)
【面试题】Java面试题汇总(无解答)
此内容会持续补充。。。 基础 short s1 1; s1 s1 1;有错吗? short s1 1; s1 1; 有错吗?String str”aaa”,与 String strnew String(“aaa”)一样吗?String 和 StringBuilder、StringBuffer 的区别?Sring最大能存多大内容?…...
)
C++---背包模型---收服精灵(每日一道算法2023.3.11)
注意事项: 本题是"动态规划—01背包"的扩展题,优化的思路不多赘述,dp思路会稍有不同,下面详细讲解。 本题偏向阅读理解,给每种变量归类起名字很有帮助哦。 切记先看思路,再看代码。(大…...

day30_JS
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、作业 二、BOM 三、定时器 四、正则表达式 零、 复习昨日 事件 事件绑定方式鼠标事件 onmouseoveronmouseoutonmousemove 键盘事件 onkeydownonkeyupon…...
)
【Java学习笔记】19.Java 正则表达式(2)
前言 本章继续介绍Java的正则表达式。 Matcher 类的方法 索引方法 索引方法提供了有用的索引值,精确表明输入字符串中在哪能找到匹配: 序号方法及说明1public int start()返回以前匹配的初始索引。2public int start(int group)返回在以前的匹配操作…...

华为云arm架构轻松安装kubeedge
先安装k8s 华为云arm架构安装k8s(kubernetes) 下载kubeedge需要的软件 官方github下载kubeedge地址 cloudcore.service文件下载地址 注意:下载对应的版本和arm架构 keadm-v1.6.1-linux-arm64.tar.gz 下面的2个文件可以不用下载,安装kubeedge时也会自动去下载到/etc/kubee…...
33--Vue-前端开发-使用Vue脚手架快速搭建项目
一、vue脚手架搭建项目 node的安装: 官方下载,一路下一步 node命令类似于python npm命令类似于pip 使用npm安装第三方模块,速度慢一些,需换成淘宝镜像 以后用cmpm代替npm的使用 npm install -g cnpm --registry=https://registry.npm.taobao.org安装脚手架: cnpm inst…...

TMS WEB Core开发Web应用优势说明
一、Delphi开发Web应用的三大框架如下: IntraWEB适合于WEB前、后端的开发,其自带的网络服务器非常强大、稳定,笔者使用Cesium框架开发的WEB GIS地理信息系统前端不需要Apache Tomcat或Nginx即可稳定运行; uniGUI是对JavaScript库Sencha ExtJS的封装,它带有两套VCL组件包,…...

人工智能简单应用1-OCR分栏识别:两栏识别三栏识别都可以,本地部署完美拼接
大家好,我是微学AI,今天给大家带来OCR的分栏识别。 一、文本分栏的问题 在OCR识别过程中,遇到文字是两个分栏的情况确实是一个比较常见的问题。通常情况下,OCR引擎会将文本按照从左到右,从上到下的顺序一行一行地识别…...

Gin框架路由拆分与注册详解析
Gin框架路由拆分与注册详解析1.基本的路由注册2.路由拆分成单独文件或包3.路由拆分成多个文件4.路由拆分到不同的APP1.基本的路由注册 下面最基础的gin路由注册方式,适用于路由条目比较少的简单项目或者项目demo // StatCost 是一个统计耗时请求耗时的中间件 func…...

2020蓝桥杯真题凯撒加密 C语言/C++
题目描述 给定一个单词,请使用凯撒密码将这个单词加密。 凯撒密码是一种替换加密的技术,单词中的所有字母都在字母表上向后偏移 3 位后被替换成密文。即 a 变为 d,b 变为 e,⋯,w 变为z,x 变为 a࿰…...

taro+vue3小程序使用v-html渲染的内容为class写了样式无效
taro小程序如果是直接引入的一个less文件是包含scoped,只是当前页面采用。<script setup>import ./index.less</script><view v-html"itehtml" class"article-content"></view>let itehtml"<p class"line…...

MASK-RCNN网络介绍
目录前言一.MASK R-CNN网络1.1.RoIPool和RoIAlign1.2.MASK分支二.损失函数三.Mask分支预测前言 在介绍MASK R-CNN之前,建议先看下FPN网络,Faster-CNN和FCN的介绍:下面附上链接: R-CNN、Fast RCNN和Faster RCNN网络介绍FCN网络介绍…...

导航技术调研(CSDN_0023_20221217)
文章编号:CSDN_0023_20221217 目录 1. 惯性导航 2. 组合导航技术 3. 卡尔曼滤波 1. 惯性导航 惯性导航系统(INS-Inertial Navigation System)是上个世纪初发展起来的。惯性导航是一种先进的导航方法,但实现导航定位的原理却非常简单,它是…...
买卖股票的最佳时机 I II III IV
121. 买卖股票的最佳时机 自己的思路:采用求最长连续子串和题目的思路 class Solution {public int maxProfit(int[] prices) {if(prices.length 1) return 0;int[] nums new int[prices.length - 1];for(int i 0;i < prices.length - 1;i){nums[i] prices[…...
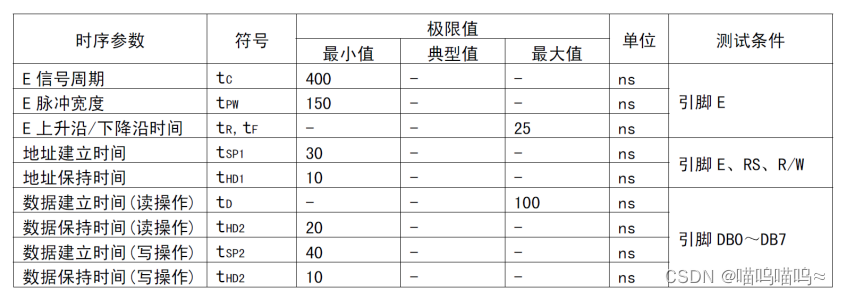
STM32—LCD1602
LCD1602(Liquid Crystal Display)是一种工业字符型液晶,能够同时显示 1602 即 32 字符(16列两行) 第 1 脚: VSS 为电源地 第 2 脚: VDD 接 5V 正电源 第 3 脚: VL 为液晶显示器对比度调整端,接正电源时对比度最弱,接地时对比度最…...

英雄算法学习路线
文章目录零、自我介绍一、关于拜师二、关于编程语言三、算法学习路线1、算法集训1)九日集训2)每月算法集训2、算法专栏3、算法总包四、英雄算法联盟1、英雄算法联盟是什么?2、如何加入英雄算法联盟?3、为何会有英雄算法联盟&#…...
【设计模式】备忘录模式和迭代器模式
备忘录模式和迭代器模式备忘录模式代码示例迭代器模式代码示例使用迭代器遍历集合的同时不能删除/增加元素总结备忘录模式 备忘录模式,也叫快照(Snapshot)模式。 在 GoF的《设计模式》⼀书中,备忘录模式是这么定义的:…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
